基于互信息与核熵成分分析的故障检测算法

郭金玉，王 哲，李 元

(沈阳化工大学 信息工程学院，辽宁 沈阳 110142)

在信息数字科技高度发达的今天，云计算、大数据分析、人工智能等全新概念促使每个行业都开始谋求技术迭代甚至商业模式的全面转型。工业领域一向重视数据分析，尤其是在故障分析与诊断方面，数据分析起到了至关重要的作用。随着化工过程规模的逐渐扩大，工业程序越发复杂，故障检测变得尤为重要和困难。一个好的故障检测算法不仅可以大大提高工业过程故障检测的效率，也能保证故障排查的精度，寻找合适的故障检测算法成为当前主要研究问题之一[1]。

最早最经典的故障检测算法—主成分分析(principal component analysis, PCA)是随着测量、数据存储和计算设备的发展而出现的。PCA将数据信息投影到主元空间和残差空间两个子空间中，并构造了以马氏距离和欧氏距离为代表的两个统计量，以检测两个子空间中的变化。其算法实现简洁、处理速度快，在处理高斯分布的高维检测数据时可以取得非常好的检测效果，因此使用最广泛。但由于PCA假定过程数据是线性的，对于某些具有特定非线性特性的复杂工业过程性能较差。近年来，一种新的非线性PCA技术—核主成分分析(kernel PCA, KPCA)[2]出现并发展迅速，通过非线性映射将输入空间映射到特征空间，然后计算高维特征空间中的主成分。与其他非线性方法相比，KPCA的主要优点是通过引入核函数避免了非线性映射和内积计算。KPCA与常规PCA相似，均通过构造Hetelling T2和平方预测误差(squared prediction error,SPE)两个统计量来分别监视主成分空间和残差空间，且均在确定统计量的置信限时基于获得的得分变量遵循高斯分布的假设，但这在非线性过程中难以满足[3]。KPCA 只利用了过程变量的方差信息，缺乏有效处理非高斯数据的能力。但实际中，工业过程数据往往是高斯与非高斯分布共存。在此情况下，Jenssen[4-5]提出一种用于非线性化学过程监测的新的多元统计数据转换方法—核熵成分分析(kernel entropy component analysis, KECA)，是一种基于角度的故障检测方法，放宽了传统PCA和KPCA方法中的高斯假设[6-8]，可用于非线性工业过程监控。相比于只考虑二阶统计量方差的KPCA，KECA 试图最大程度保留原始数据的熵值，有助于有效提取数据中的高阶统计量即非高斯信息，对于某些故障的检测卓有成效，但因为在数据处理过程中失去对数据高维信息的捕捉，对微小故障的检测较传统的分析方法相对弱势。齐咏生等[9]改进了传统的KECA方法，提出一种CS(Cauchy-Schwarz)统计量，该统计量在微小故障的检测方面表现突出，但由于CS统计量是通过向量之间的夹角获得的，对于样本信息熵的处理不如互信息，导致检测效果不稳定。互信息(mutual information, MI)[10]是一种脱胎于信息论的信息度量方法，可被看成是一个随机变量中包含关于另一个随机变量的信息量，或者说是一个随机变量由于已知另一个随机变量而减少的不确定性，可以高效地估计出两组随机变量相互依赖的程度，还可以有效地考虑高维度统计量[11-12]。但这种方法目前很少应用在工业数据分析领域[13-14]。

本研究将KECA与MI结合起来，提出一种基于互信息和核熵成分分析的故障检测算法，利用新型统计量—基于互信息的平方预测误差(squared prediction error based on mutual information, MISPE)，弥补KECA在故障检测时过多丢失高维度信息的问题。相比于之前单纯对向量夹角或距离的度量，MI的引入能够更加精细地表达变量之间的关系，大大提升KECA方法对于非微小故障的检测效率。

1 算法提出

1.1 KECA算法

假设p(x)是生成数据集D:x1,x2,…,xN的概率密度函数，则瑞丽熵(Rényi entropy)[15]为：

(1)

(2)

式中:kσ(x,xt)是以xt为中心的Parzen窗，σ是窗口宽度。使用样本均值来近似估计V(p)，得到

(3)

式中：K是N×N的核矩阵；I是一个N×1的单位向量。基于可用样本获得的瑞丽熵估计量就是相应核矩阵的元素。

将核矩阵进行特征分解，K=EDET。其中：D为特征值矩阵；D=diag(λ1,λ2,…,λN)；E=(e1,e2,…,eN)为特征向量矩阵。重写式(3)，得到：

(4)

在KPCA中，仅仅基于特征值的大小选择特征值和特征向量来执行降维，而从熵的角度来看，特征向量熵的估计值同时受特征值和特征向量的影响。因此在式(4)中，Ψi的值可以用作瑞丽熵的估计。

对于输入数据集D:x1,x2,…,xN，给定一个核函数φ(·)，定义从输入空间到核特征空间的映射xi→φ(xi)(i=1,2,…,N)，核特征空间的数据集表示为Φ=[φ(x1),φ(x2),…,φ(xN)]。本研究选用高斯核函数将样本数据映射至高维空间，高斯核函数对于数据中的噪音有着较好的抗干扰能力，其参数决定了函数作用范围，超过这个范围，数据的作用就“基本消失”，通常是通过交叉验证获得有效的核参数。

KECA可以看作是将Φ投影到重要的子空间Us上所获得的s维数据转换，这个重要的子空间Us是由那些对数据的瑞丽熵估计贡献最大的s个KPCA主轴组成的,不一定与前面的特征值相对应[17]。转换如下:

(5)

式中，得分矩阵T=[t1,t2,…,ts]。新的测试数据通过函数Φ′投影到子空间上,即可得到得分矩阵

(6)

式中,K′=Φ′TΦ。定义输入数据集的残差矩阵

(7)

1.2 基于互信息的新型检测方法

在两个随机变量之间的统计依赖性度量中，互信息由于其信息论背景而被引入。MI在估算KECA算法中每个样本的实际统计独立性中起着重要作用。一个连续随机变量x=(x1,x2,…,xn)的香农(Shannon)熵定义为：

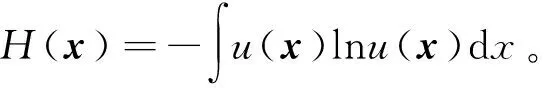
(8)

式中u(x)是x的概率密度函数。

对于随机变量x和y，x中包含y的信息量可以由互信息度量，其定义为：

(9)

式中:ux,y(x,y)是联合概率密度函数，ux和uy是x和y的边缘概率密度函数。

根据变量的熵估计互信息为：

I(x,y)=H(x)+H(y)-H(x,y)。

(10)

式中:H(x)和H(y)是x和y的边缘熵，H(x,y)是联合熵。联合熵的计算公式为：

(11)

值得注意的是，在实践中通过计算积分和求和的互信息估计是密集且效率低的。为了减轻计算负担，一种基于香农熵的Kozachenko-Leonenko估计量的最近邻策略被提出，用于对互信息的数值估计[18-19]。首先，通过最近邻技术估计联合熵为：

(12)

假设zi=(xi,yi)代表空间中一个坐标点，则式(12)中的ε(i)/2是点zi到其第l个近邻的距离；εx(i)/2和εy(i)/2分别表示相同点投影到X和Y子空间的距离,显然ε(i)=max {εx(i),εy(i)}。此外，ψ(x)=Γ(x)-1dΓ(x)/dx为双伽玛函数，Γ(x)=(x-1)!是伽马函数，其中dx和dy分别表示x和y的维数，cd=πd/2/Γ(1+d/2)/2d是欧几里得范数的d维单位立方体的体积。对于边缘熵H(x)或H(y)，可以通过关节空间投影来估计：

(13)

式中，τx(i)是与xi的距离小于εx(i)/2的点数。式(10)减去式(12)、(13)，得：

I(x,y)=ψ(l)-〈ψ[τx(i)]+ψ[τy(i)]〉+ψ(n)。

(14)

式中〈·〉表示随机样本所有可能实现的平均值。在MI的最终方程式中减去用于度量近邻子空间大小的参数ε(i)和cd，说明互信息的估算结果与近邻空间的数据规模无关。这种方法可以扩展到计算任意维的变量x和y之间的多维互信息。因此，对于基准数据集的残差矩阵FR和监视数据集的残差矩阵FM，多维互信息的计算公式为：

I(FR,FM)=ψ(l)-〈ψ[τR(i)]+ψ[τM(i)]〉+ψ(n)。

(15)

式中:n代表残差空间中样本的大小，τR(i)和τM(i)分别代表由εx(i)/2和εy(i)/2确定的近邻空间中的点数。式(15)说明FM和FR之间的互信息值越小，相异指数值越大。换句话说，如果相异指数较大，则当前监视的操作模式明显不同于基准条件，被视为异常。

相比KPCA，KECA虽然考虑了数据信息熵丢失的问题，但没有充分考虑高阶统计量。因此，本研究通过两个近邻空间之间基于多维互信息的统计独立性来表征差异性。由于KECA所提取的熵成分可以是非线性、非高斯的，而互信息可以同时捕捉数据中的非高斯统计关系和各种隐藏信息，因此本研究将互信息和传统KECA方法中的SPE统计量结合，得到一个可以面向几乎所有类型数据分布形式且对于高维统计信息更加敏感的新统计量—MISPE。每个样本的MISPE统计量定义为：

(16)

式中

(17)

本研究选用核密度估计(kernel density estimation，KDE)确定样本统计量的控制限。核密度估计是一种非参数估计，既不需要数据的先验知识，也不做任何假设，被广泛用于确定数据分布非正态或未知时的控制限。公式为：

(18)

式中：h为带宽，K代表高斯核函数。

1.3 基于MIKECA的故障检测步骤

基于MIKECA的故障检测步骤包括两部分：离线建模和在线监控。

1) 离线建模

正常数据用D(N×M)表示，其中N代表样本数量，M代表每个样本所含变量的个数。将数据集D作为训练数据按照以下步骤进行处理。

Ⅰ 给定核函数以及核参数，利用样本数据构建KECA模型，利用式(6)求出得分矩阵T=[t1,t2,…,ts]，并利用式(7)计算残差矩阵F(N×M)；

Ⅱ 利用式(17)计算样本数据的监测统计量SPE；

Ⅲ 从F中选出一个样本作为标准样本FR，求出F中各个样本与标准样本的互信息，利用式(16)得到新的监测统计量MISPE；

Ⅳ 计算监测统计量的控制限MISPElim。

2) 在线监控

Ⅰ 对测试数据集Dnew，按离线建模数据的均值与方差对测试数据标准化；

Ⅱ 把当前测试数据投影到KECA模型中，利用式(6)提取得分向量Tnew，利用式(7)计算残差矩阵FM；

Ⅲ 利用式(17)计算测试数据的监测统计量SPEnew；

Ⅳ 根据式(16)，利用残差矩阵FM得到新的监测统计量MISPEnew；

Ⅴ 与控制限MISPElim进行比较，如果统计量超出相应的控制限，即可判断工业过程发生了故障；反之，则认为测试数据正常，返回继续进行下一个测试数据的监测。

2 仿真结果与分析

2.1 TE过程

田纳西-伊斯曼(Tennessee Eastman,TE)过程是评估本研究提出的监测方法有效性和实用性的重要实验对象，其工艺流程图如图1所示，由5个主要单元操作组成，包括化学反应器、冷凝器、循环压缩机、气/液分离器和汽提塔。TE过程由4种气态反应物A、C、D、E和惰性的气态组分B参与反应，生产出两种液态产物G和H以及副产物F。反应器产物流通过部分冷凝器冷却，并进料至气/液分离器中进行组分分离。此外离开分离器的蒸汽流通过压缩机再循环至反应器进料流。净化一部分循环物流以防止过程中惰性和副产物的积累[20]。同时，来自分离器冷凝的组分(物流10)被泵入汽提塔。离开汽提塔的产品G和H在下游操作中进一步处理。

图1 TE过程流程图

TE过程包括1种正常工况和21种可操作的故障工况。表1为TE过程21种故障的说明。正常和故障工况下的采样时间间隔为3 min。在正常工况下，过程运行48 h产生的960个数据被采集作为正常数据样本，21种故障工况是在过程稳定运行8 h后引入，故采集的960个数据中前160个数据不含故障，后800个数据含有故障。将正常工况下的960个数据作为训练样本，所有含故障数据作为测试样本。

表1 TE过程的故障说明

2.2 仿真结果

选取TE过程中的故障7、11、17和21作为测试数据集，将KPCA、KECA的SPE、CS统计量与本研究提出的MIKECA进行对比, 通过故障检测率(fault detection rate，FDR)和误报率(false alarm rate，FAR)两个指标评估算法的好坏。

以故障17为例，图2是4种方法进行故障检测的仿真结果。对于故障17，4种方法都对故障样本和正常样本进行了大致上的甄别。KPCA的误报现象最为严重，同时也有一定数量的漏报。KPCA在选取主成分时仅考虑了特征值的大小，没有充分考虑高阶统计量，因此KPCA无法有效提取过程数据中的非高斯特征，导致检测效果差。相比KPCA，KECA的误报有了明显改善，但是KECA也漏报了相当一部分的故障样本。KECA尽可能地保留原有数据的熵值，改善了误报现象严重的问题，但是没有考虑投影后数据的结构特征，因此总体检测效果没有大幅度地提升。与KECA相比，CS统计量弥补了基于距离的监测指标对那些故障幅度较小、数据结构变化不明显的故障监测效果较差的不足，一定程度上提高了KECA算法的检测率，降低了误报率。但是这种基于向量夹角计算得出的统计量无法兼顾到样本的高维信息，误报率也相对偏高。对比其他3种方法，本研究的MIKECA算法的误报率最低，而且故障检测率最高。MIKECA不仅结合了KECA选取主成分的优势，还利用互信息捕捉样本高维信息，因此总体检测效果明显优于其他算法。

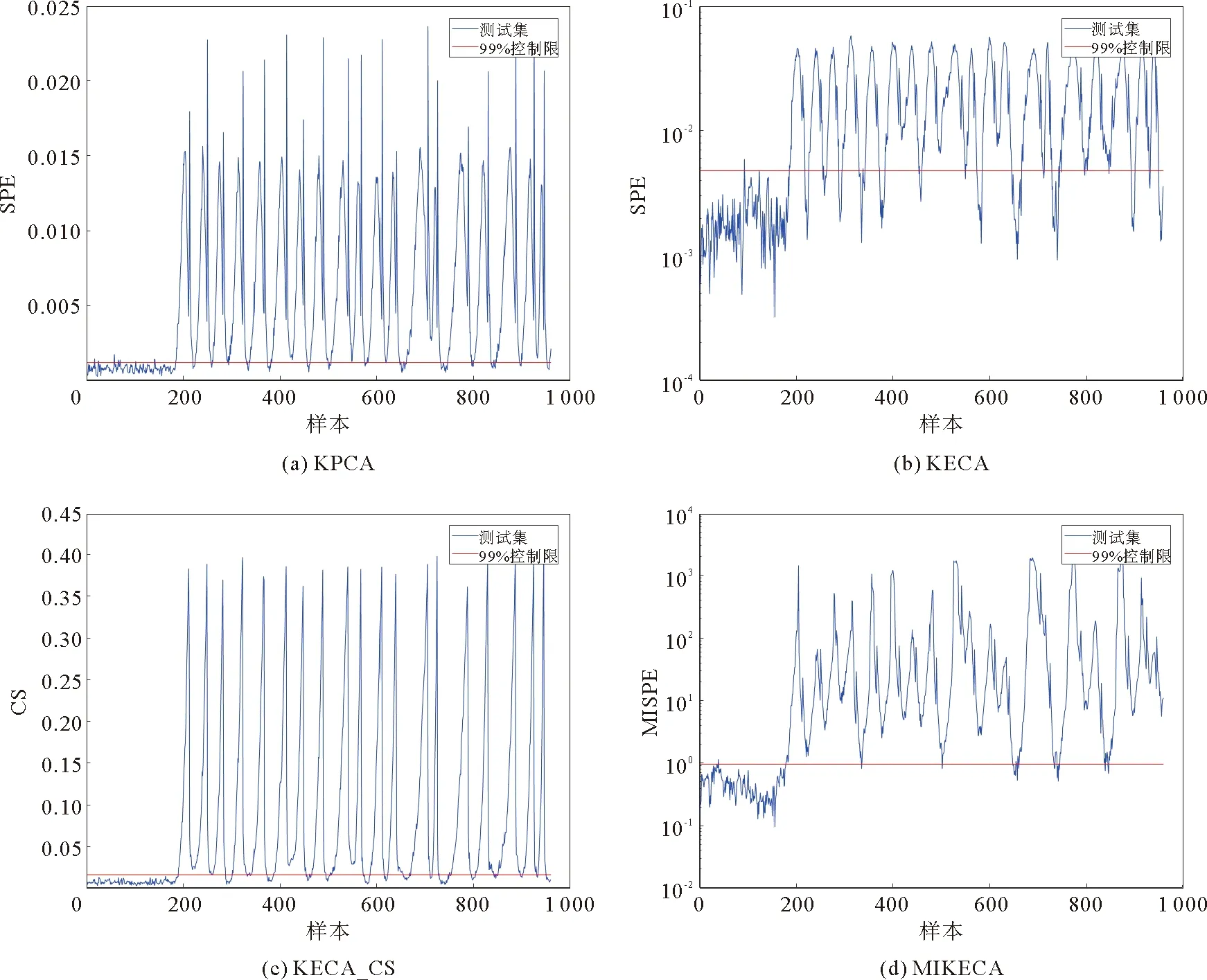
图2 4种算法对故障17仿真结果对比图

表2列出4种算法的FDR与FAR对比。由表2可知，对比其他3种方法，MIKECA算法对4个故障检测的误报率较低，而且检测率最高，验证了该方法在故障检测中的有效性和优势。

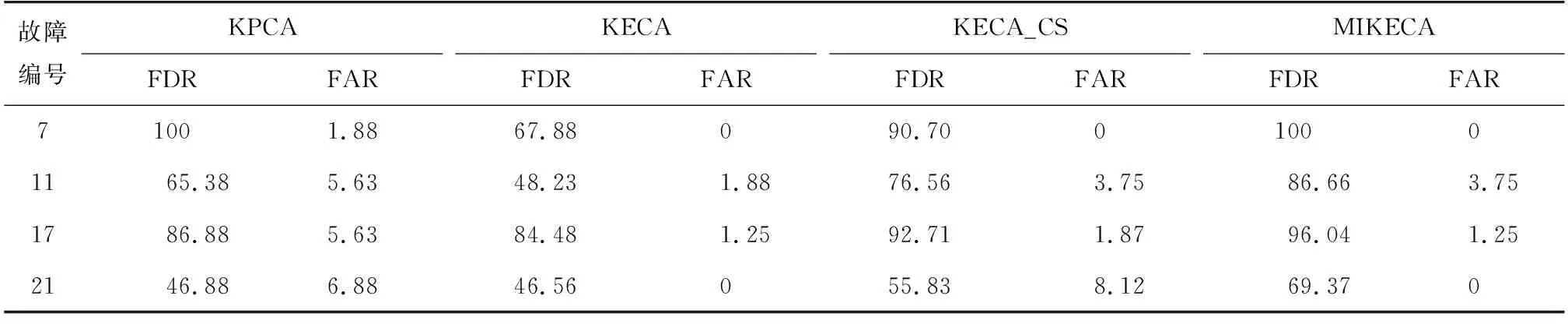
表2 4种故障检测算法的结果对比

3 结论

本研究提出一种基于互信息和核熵成分分析的故障检测算法MIKECA，并将其应用于田纳西-伊斯曼过程的故障检测。该方法与原来基于角度的CS统计量不同，不仅充分捕捉了过程的非高斯特征，而且通过互信息的计算，更兼顾了各种维度的数据统计信息。监测结果表明，MIKECA的故障检测效果优于KPCA、KECA算法，具有最可靠的故障检测能力。

未来的工作集中在故障诊断部分，通过基于差异的模式识别来隔离故障变量。因此，调整所提出的方法以适应更复杂的批量操作环境值得进一步研究。此外，该方法在其他化工过程中的应用也需要进一步探讨。