随机时滞马尔可夫跳跃系统的有限时间H∞控制
刘西奎,刘文成,李 艳,庄继晶
(1.山东科技大学 数学与系统科学学院,山东 青岛 266590; 2.山东科技大学 电气信息系, 山东 济南 250031)
众所周知,马尔可夫跳跃系统是由多个模态或子系统组成的切换系统,系统在各个子系统间的切换服从一定的概率分布。该系统适合描述突变现象,如零部件故障、子系统之间关联改变以及突发性环境扰动等,被广泛应用到电力系统、制造系统、通讯系统等工程领域。近年来,关于马尔可夫跳跃系统的研究取得了丰富的成果。文献[1]分别讨论了连续和离散时间马尔可夫跳跃系统的稳定性和镇定问题。文献[2]使用量化方法研究了一类具有时变转移概率的奇异马尔可夫跳跃系统的镇定问题。文献[3]针对离散时间马尔可夫跳变系统,结合有限时间理论,给出了有限频段和有限时间两种尺度的H∞滤波器设计方法。文献[4]研究了马尔可夫跳跃系统的不定平均场随机线性二次最优控制,通过定义一种广义黎卡提差分方程,得到最优控制的一般形式。文献[5-6]分别研究了离散时间和连续时间随机马尔可夫跳跃系统的H-指数问题,并用于故障检测滤波器设计。
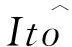
符号表示:E[·]是[·]的数学期望;矩阵M∈Rm×n,M>0(M≥0) 表示M是正定(半正定)矩阵;λmax(M)与λmin(M)分别表示矩阵M的最大特征值和最小特征值; (M)★≜M+MT。
1 定义和问题描述
考虑如下时滞随机马尔可夫跳跃系统:
(1)
式中:x(t)∈Rn是系统状态,u(t)∈Rm是控制输入,z(t)∈Rq是控制输出;时滞τ满足τ≥0;φ(t)是定义在[-τ,0]的连续函数;ω(t)是定义在概率空间(Ω,F,Ρ)上的一维Wiener过程,满足E[dω(t)]=0,E[d2ω(t)]=dt。ω(t)与{θt,t≥0}相互独立。随机过程{θt,t≥0}是一个右连续的马尔可夫链,在集合S={1,2,…,N}中取值,其转移概率矩阵为Π=[πij]N×N,πij是由状态i到状态j的转移率,满足转移概率
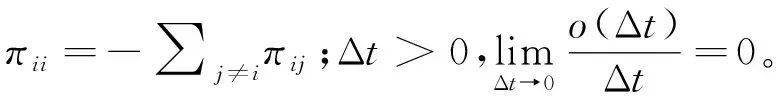
外部扰动v(t)满足
(2)
为简单起见,当θt=i时,适当维数的常数矩阵A(θt),Aτ(θt),B(θt),C(θt),Cτ(θt),D(θt),G(θt),F(θt),H(θt),Hτ(θt)和D1(θt)分别记作Ai,Aτi,Bi,Ci,Cτi,Di,Gi,Fi,Hi,Hτi和D1i。
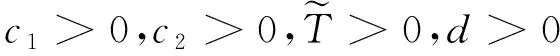
(3)
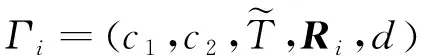
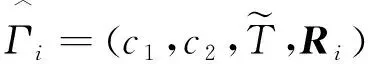
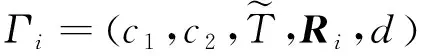
引理 1(Gronwall不等式)[22]设f(t)是一个非负函数,如果存在非负常数p和q,满足
则
引理2(舒尔补引理)[23]对于实矩阵H,实对称矩阵S,正定矩阵U,下列不等式等价:
S+HU-1HT<0,
2 有限时间有界性分析
本节讨论u(t)=0时,系统(1)的有限时间有界性。通过线性矩阵不等式方法,给出系统(1)有限时间有界的充分条件。
定理1对于正常数η,如果存在正常数λi1,λi2,正定矩阵Pi,Oi,Q,满足
(4)
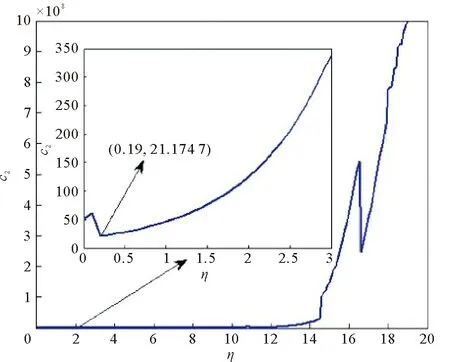
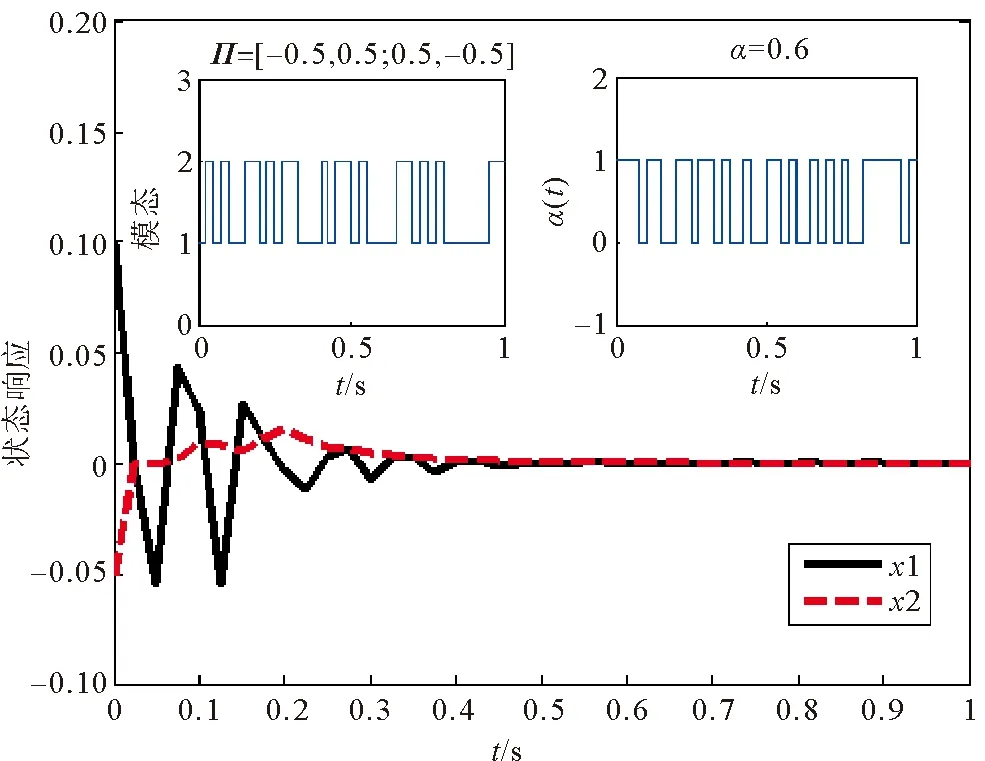
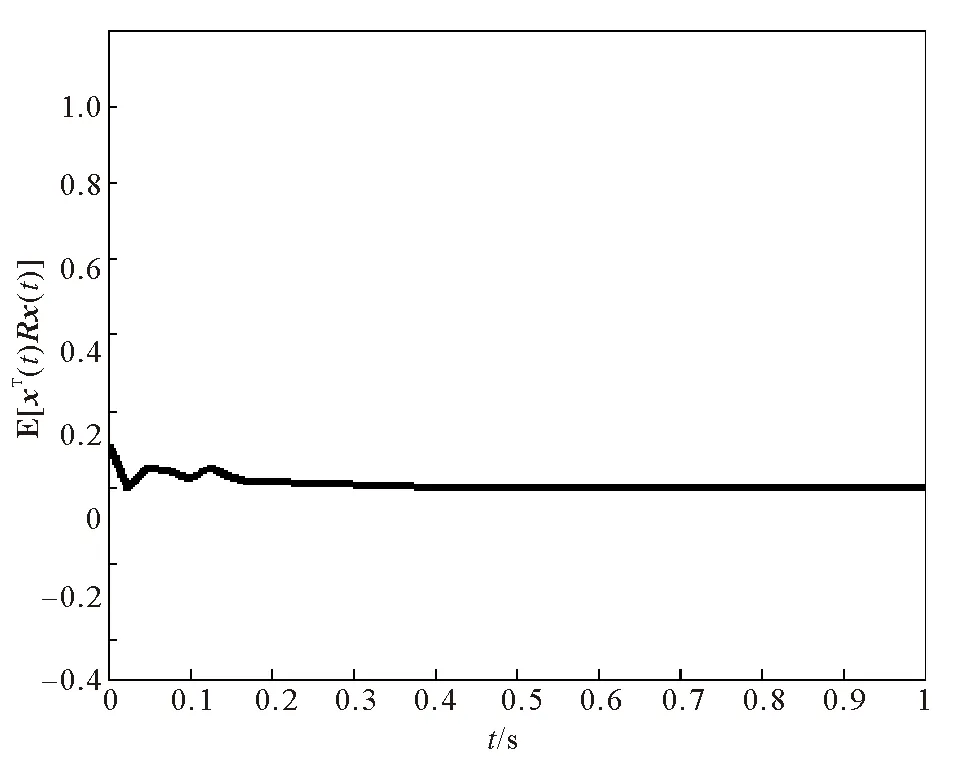
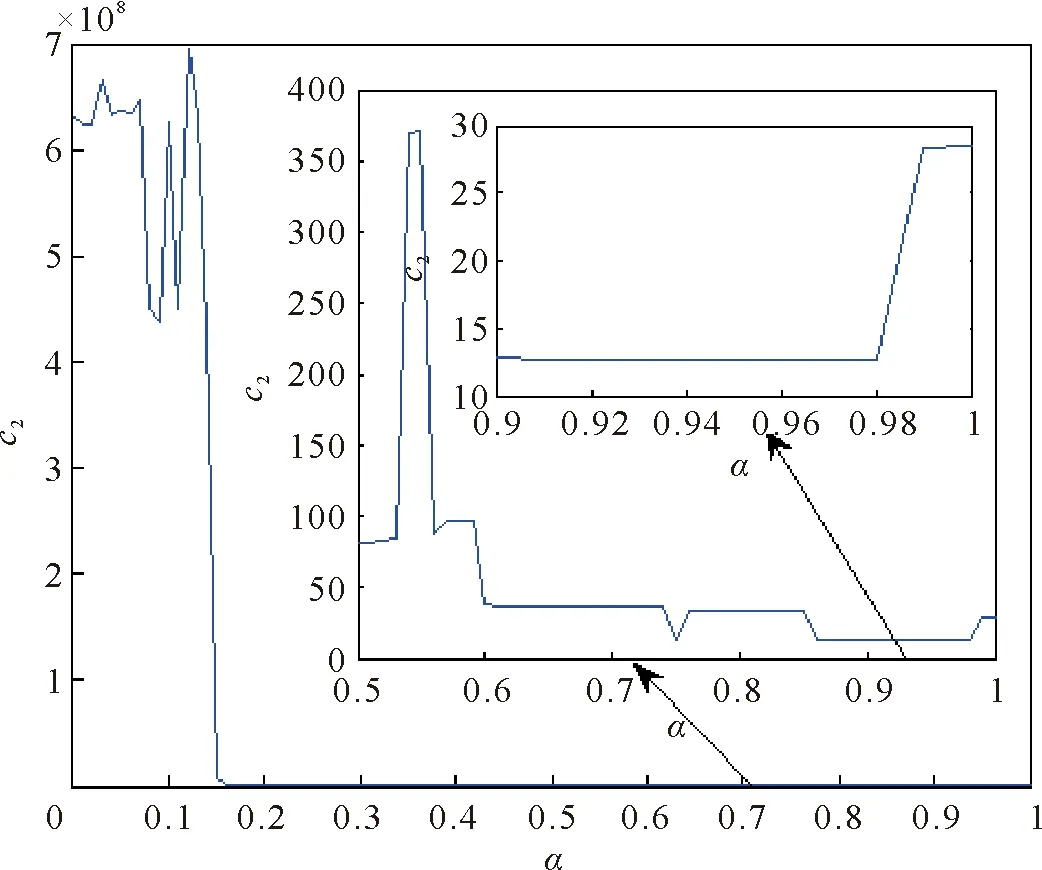
Q (5) (6) (7) 证明:构造Lyapunov函数 (8) 进而 (9) 式中Ξ=Cix(t)+Cτix(t-τ)+Fiv(t)。 由引理2,式(4) 等价于 左右两边分别乘以[xT(t)xT(t-τ)vT(t)]T及其转置,并对比式(9), 得 (10) 式中V1(xt,θt=i)=xT(t)Pix(t)。进一步, (11) (12) 应用引理1,得 (13) (14) (15) (16) 结合式(13)~(16),则 (17) 注2当Fi=0,Gi=0时,定理1为系统(1)有限时间稳定的充分条件。从而,定理1退化为文献[28]的定理1。 本节提出一种新型控制器 u(t)=α(t)K(θt)x(t)+(1-α(t))Kτ(θt)x(t-τ), (18) 式中:K(θt)和Kτ(θt)表示控制器增益,随机变量α(t)是伯努利变量,满足 Pr{α(t)=1}=α, Pr{α(t)=0}=1-α。 显然 E[α(t)-α]=0,E[(α(t)-α)2]=α(1-α)=β2。 将控制器(18)代入系统(1),得 (19) 接下来,在定理1的基础上,给出闭环系统(19)有限时间H∞有界的充分条件。 (20) (21) (22) (23) (24) 证明:对于闭环系统(19),选择Lyapunov函数(8),则 =E[WTPix(t)]+E[xT(t)PiW]+E[WTPiW]+xT(t)Qx(t)- 因为E[α(t)-α]=0,E[(α(t)-α)2]=α(1-α)=β2,所以 (25) (26) 得 (27) (28) 式中: 对式(28)两边分别乘以矩阵[xT(t)xT(t-τ)vT(t)zT(t)]T及其转置,并与式(25)对比, 得 (29) 在零初始条件下,对式(29)两边积分并取数学期望,得 (30) 根据引理1,有 (31) 从而 由式(29),进一步得 (32) (33) 且 (34) 由引理2, 可知式(22)和(33)等价。通过式(23)和(26),可以得式(34),即式(22)和(23)等价于式(6)。令定理1中的Oi=-γ2I,则式(11)与(32)等价,式(7)与(24)等价。其余证明与式(12)~(17)证明相同,在此省略。 注3当α(t)=1和0时,控制器(18)分别为状态反馈控制器u(t)=K(θt)x(t)和时滞状态反馈控制器u(t)=Kτ(θt)x(t-τ)。与文献[17-20]中的状态反馈控制器和文献[21]中的时滞反馈控制器对比,控制器(18)更具有一般性,可以用于网络控制系统、单接点机械手臂等实际系统。 为验证前述定理的有效性,考虑具有两个模态的随机时滞马尔科夫跳跃系统(1),其参数如下。 模态1: 模态2: 转移概率矩阵为: 由定理2可得η的可行域为[0,18.99], 图1和图2分别是η与c2和γ的关系曲线图。 图1 η∈[0,20]时,c2的变化 图2 η∈[0,20]时,γ的变化 从图1和图2可以看出,当η=0.19时,c2取得最小值21.174 7,对应的γ=2.639 9。 K1=[-1.464 9-1.065 5],Kτ1=[0.226 0-0.272 8], 图3 状态x(t)的响应曲线 图4 E[xT(t)Rx(t)]的演化 图5表示c2和α的关系,其中小图是α分别在闭区间[0.5,1]和[0.9,1]取值时c2的曲线图。当α(t)的数学期望α=0.98时,c2取最小值。即α=0.98时,控制器(18)的保守性最小。与文献[20]的状态反馈控制器(对应α=1)相比,控制器(18)保守性更小。 图5 c2与α的关系 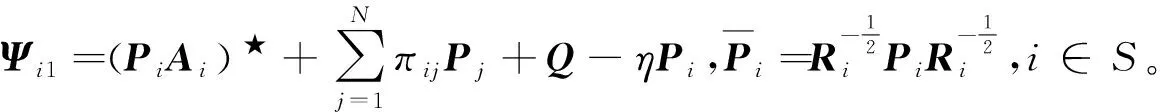

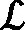


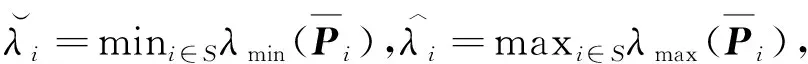


3 通用控制器的设计
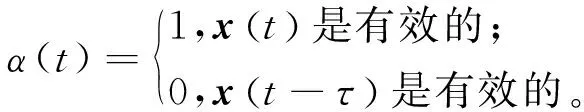
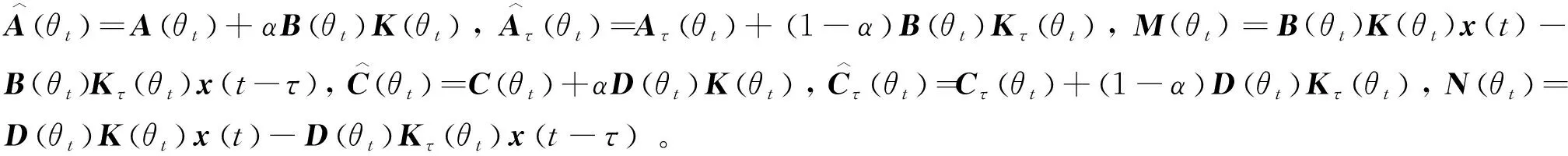
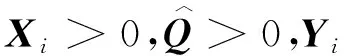

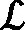
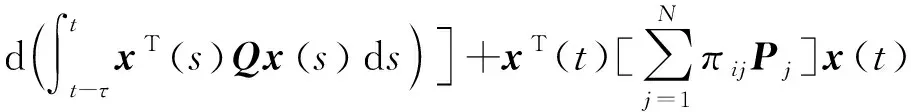
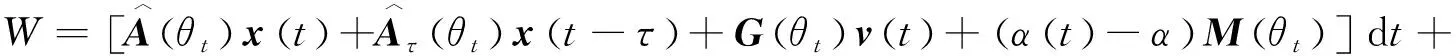
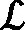
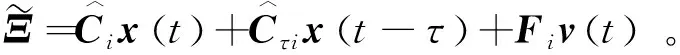
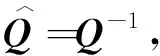
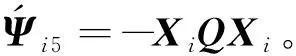
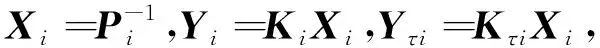
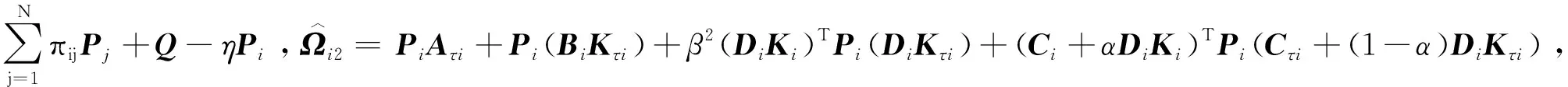
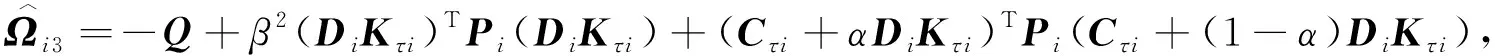
4 数值算例

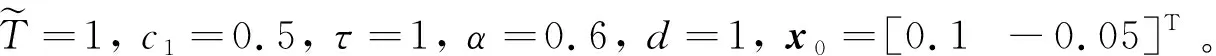

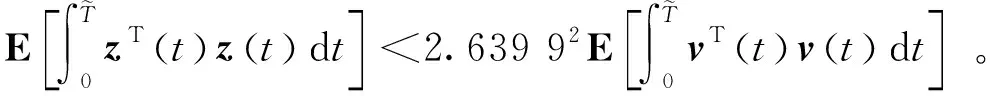
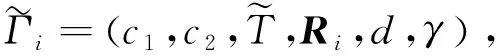
5 结论

