基于熵理论的电网安全局面评估函数的构建及应用

于 群，王文山，杨学涛

(1.山东科技大学 电气与自动化工程学院，山东 青岛 266590； 2.中国电力科学研究院，北京 100192)

近年来，我国相继建成了1 000 kV特高压交流、±800 kV特高压直流等多个特高压输电工程，形成了世界上规模最大、电压等级最高的交直流混联电网[1-2]，相应地对电网的安全运行提出更高要求。电力系统一旦出现安全问题，往往造成局部甚至大规模的停电事故，直接影响到社会稳定和经济发展[3-4]。针对电网的可靠性，文献[5]从电网的拓扑结构入手，基于复杂理论提出一种网络结构脆弱性分析方法，得出电网的脆弱性与其拓扑结构密切相关的结论；文献[6]根据有功潮流介数指标及系统输电效率指标提出一种辨识电网关键线路的方法；文献[7]基于电力系统的自组织临界性，提出一种辨识电网薄弱节点的方法。以上研究更多是关注电力系统中某一元件的重要程度，无法反映系统整体的运行状况是否安全与可靠。

研究[8-9]发现，虽然不同类型电网发生大停电事故的表现形式不同，但大部分原因是由一个初始扰动或一系列扰动引起的潮流转移导致电网功率不平衡，开关状态改变，从而引发大停电事故，因此可以通过描述电网的运行状态来分析电网的大停电特征。作为衡量系统能量分布是否均匀的熵，其理论最早应用于热力学定律，近年来在复杂理论中也越来越受到重视，并逐渐成为一个研究复杂系统的重要工具。文献[10]基于熵的基本原理，提出一种预测损失负荷的最大熵模型；文献[11]通过支路开断熵和潮流负载熵电网稳态时支路的运行情况，同时预测电网受到扰动后的运行趋势；文献[12]利用电压变化量泰尔熵和潮流变化量泰尔熵，结合熵权法和层次分析法对电网中的关键线路进行辨识。

针对电网的安全运行问题，本研究利用熵理论，计及多个指标，在统筹考虑电网的网络结构特性和实际运行特征的情况下，构建一种评估电网安全性的局面评估函数模型，对预防电网连锁故障和大停电事故的发生具有借鉴意义。

1 局面评估函数与熵理论

1.1 局面评估函数简介

局面评估函数是用来评估研究对象整体以及局部性能的一种数学函数模型，多用于棋局局面的分析与博弈研究。文献[13]利用局面评估函数建立一种中国象棋博弈对局的数学模型，对评估值进行优化，有效提高了棋局对弈的获胜概率。文献[14]针对六子棋构建评估函数，并结合全局路和局部路的特点，使评估函数在保持精度的基础上提高了执行效率，可以对不同的局面进行分析估量。

在电力系统中，局面就是指系统经过若干时间的复杂运行后所处的状态。对电力系统所处运行状态的准确判断有助于维持系统的安全运行。而要直观理解当前的局面，就需要建立局面评估函数，将影响电网安全的因素用数学模型表示出来，以此评估系统在当前局面下的运行状况。

1.2 熵理论简介

熵的宏观意义是衡量系统能量分布是否均匀的一个指标，可以体现物体当前所处状态是否稳定，系统变化的方向是否改变。若系统能量分布均匀，那么其有序程度就相对较低，熵越大；反之，有序程度相对较高，熵越小。基于此，目前熵理论在电网的无序量度中被广泛应用[15-16]。而作为一个拥有能量平衡特征的电力系统，同时还具有复杂系统的特性，所以系统内部能量分布的熵变过程可用来描述系统的稳定状态。

当系统处于多个不同状态，且每种状态出现的概率为P(Xi)(i=1,2,…,m)时，系统的熵可定义为:

(1)

式中：C为常数，m为状态数。由式(1)可知，熵有如下几种性质。

1) 连续性。熵值应当连续，概率值的小幅变化，只能引起熵的小幅变化。

2) 可加性。系统的熵等于各个状态的熵之和，与过程如何被划分无关。

3) 非负性。由于概率P(Xi)∈[0,1](i=1,2,…,m)，故系统的熵一定是非负的。

4) 极值性。当系统的状态概率全部相等时，系统的熵值达到最大。

2 局面评估函数模型

2.1 局面评估函数指标

电力系统运行状态的判断是一件十分复杂的事情，在很大程度上局面评估函数的建立依赖于具体的系统网络结构特性与实际运行特征。只有对一定状态下电力系统的局面做出正确判断，才能评估出系统的安全运行状态，并以此采取相应的措施来减少连锁故障的发生。因此，必须将局面，即整个电力系统内节点电压、线路潮流、系统负载等对系统安全运行可能会产生影响的因素构成的总和进行量化并建立评估函数数学模型，才能尽可能地对整个系统的运行状态做出合理、准确的判断。

2.1.1 网络结构熵

电力系统依靠各个区域之间的协调交互，形成网络来完成一系列的输电任务。其中，节点和网架结构是电力系统研究中的重要组成部分。分析电力系统节点的重要性有助于局部故障的定位，而网络结构可用来探索不同区域类型之间的差异。文献[17]提出电力系统在正常运行中，其自组织临界状态与系统网络结构密切相关。所以，可将网络结构熵作为构建局面评估函数的一个指标。

在传统的复杂网络理论中，称Ii为第i个节点的重要度[18]，

(2)

式中：N表示网络中的节点数目；ki表示第i个节点的连接度。当ki=0时，讨论该节点无意义，因此假设ki>0，从而Ii>0。

对于配电网，除了考虑网络节点的重要度外，还应当考虑节点的实际功率。

(3)

式中：Di表示节点i的节点度数；Pi表示注入节点i的有功功率。

Di同时考虑了节点在配电网中的结构特性和实际运行特征，与节点重要度相比，更加契合配电网的特点。所以，可得网络结构熵

(4)

2.1.2 有功裕度熵

节点有功裕度指标体现了系统中节点在受到功率扰动后维持稳定的能力，也可以间接体现系统对于负荷变化的承受能力。指标越大，表示该节点对功率扰动的承受能力越强。节点有功裕度指标定义为：

(5)

式中：Pimax为系统中节点i的极限传输功率；Pi为系统中节点i当前运行时的有功功率。

因此，有功裕度熵

(6)

2.1.3 电压裕度熵

电力系统的电压稳定主要研究系统在当前运行工况下，距离系统的电压崩溃点之间的裕度问题[19]。节点电压裕度指标体现了系统中的节点在受到电压扰动后维持稳定的能力，也可以间接体现系统对于无功储备的能力。指标越大，表示该节点对电压扰动的承受能力越强。节点电压裕度指标定义为：

(7)

式中：Uicr为系统中节点i的临界电压；Ui为系统中节点i当前运行时的电压。

因此，电压裕度熵

(8)

2.2 局面评估函数的建立

2.2.1 指标归一化处理

为了使局面评估函数的结果更具有准确性，应当消除各个指标在单位和数量级上的差异。

对值越大越有利型的指标进行归一化处理：

(9)

对值越小越有利型的指标进行归一化处理：

(10)

式中：Hni为第n个指标的第i个熵值；maxHni和minHni分别为各个指标的最大熵值和最小熵值。

2.2.2 基于熵权法的各指标权重计算

熵权法是一种相对客观的赋权方法[20]，该方法中综合权重是根据各评估指标所提供信息量的多少来确定的。如果某一指标所提供的信息量越多，那么其在综合评估中就越重要，权重也越高；反之，该指标越不重要，权重越低。设归一化后第n个指标的熵为Sn，则

(11)

(12)

式中：eni为第n个指标的第i个归一化后的指标值。当yni=0时，令ynilnyni=0。

指标n的权重为：

(13)

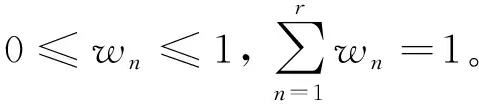
2.2.3 调整因子

由于不同电力系统的运行方式及运行特征均不相同，因此不能使用同一种风险等级标准进行电网安全性判断。为了增加该局面评估函数的普适性，定义调整因子

(14)

式中：Vb为划分电网运行风险等级的系统节点电压；Vs为局面评估函数所评估的目标系统节点电压。

2.2.4 局面评估函数

基于各评估指标得到其归一化后的指标值为：

(15)

该运行状态下各个指标值的权重为:

(16)

综上所述，定义评估电网运行状态的局面评估函数为:

(17)

(18)

式中：E(t)为状态t时电网的局面评估函数值；R为常数，为了使所得结果更加清晰直观，取R=20；Ii为局面平衡矩阵。

3 算例仿真

3.1 IEEE39节点系统局面评估

本研究算例使用IEEE39节点系统，其拓扑结构如图1所示。其中，x轴与y轴确定IEEE39节点系统图中各线路的相对位置。该系统共有10台发电机、19个负荷、46条线路。利用MATLAB R2016a软件对系统进行建模仿真，仿真流程如图2所示。

图1 IEEE39节点系统图

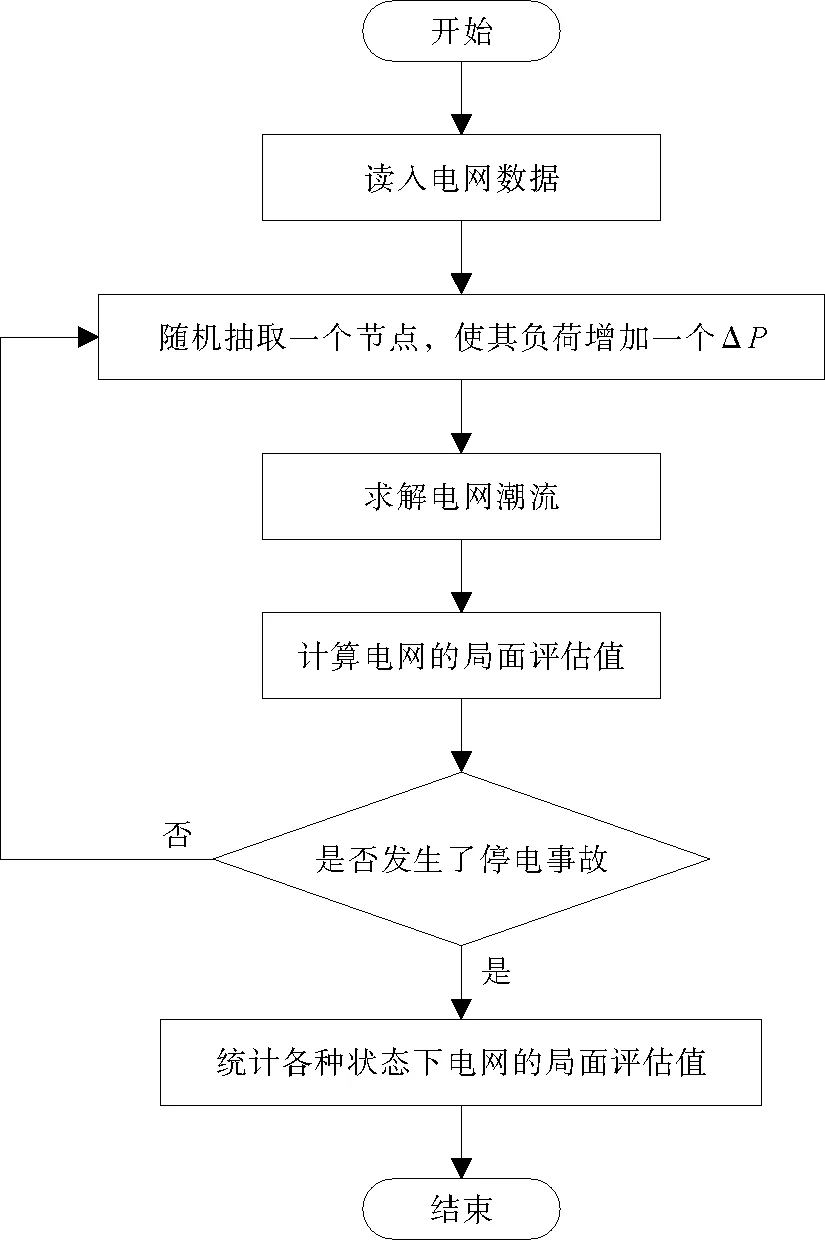
图2 局面评估函数基本流程图

应用前文所述的权重计算方法，基于网络结构熵、有功裕度熵和电压裕度熵得到归一化后的指标值分别为:

(19)

(20)

(21)

其中，网络结构熵归一化时使用式(9)。由于有功裕度熵指标和电压裕度熵指标对电网局面评估起反方向作用，即指标熵值越大，系统承受功率扰动和电压波动的能力越强，因此需使用式(10)对有功裕度熵及电压裕度熵进行归一化处理。初始状态下随机选取10个节点，各个指标归一化后的熵值如表1所示。

表1 各指标归一化后的熵值

从表1可以看出，归一化后的网络结构熵、有功裕度熵和电压裕度熵指标值不尽相同，主要原因是不同评价指标在进行评估时对电网的影响侧重点不同，所得结果也不可能完全相同。由式(11)～(13)可以得到不同指标的权重值如表2所示。

表2 各指标权重值

利用熵权法分配权重后使用局面评估函数进行评估，此时Vb=Vs。在仿真过程中等间距选取10次评估结果，所得评估值如表3所示。根据表3可得局面评估函数值拟合曲线，如图3所示。

图3 仿真过程中电网局面评估函数值变化曲线

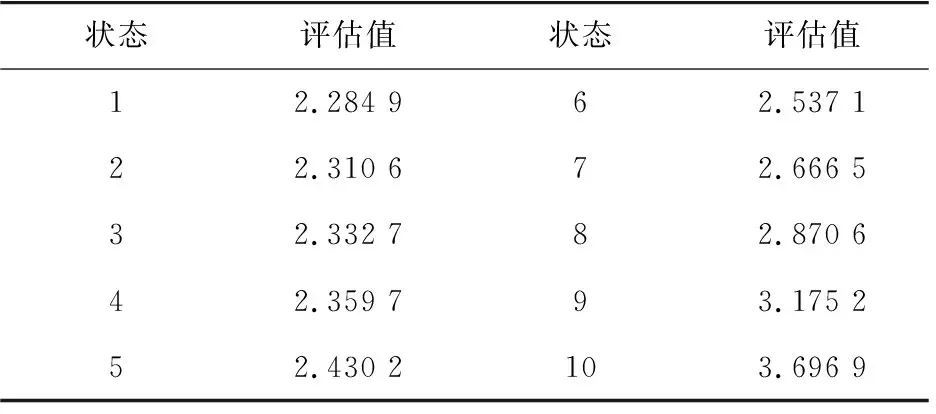
表3 仿真过程中电网局面评估函数值

重复进行多次仿真，随机选取其中3次，在每次仿真过程中等间距选取10次评估结果，并将其表示在同一坐标系内，如图4所示。

根据局面评估函数所得到的系统评估值，可以定量的描述电网运行的风险等级。评估值越大，说明电网的风险等级越高。从图4可以看到，在评估值小于2.5时，电网局面评估值变化不大，说明此时系统的抗干扰能力较强，电网运行在安全状态；当评估值在[2.5,3]时，电网局面评估值有了显著的变化，此时系统受到较大扰动，抗干扰能力下降，但还不至于发生大停电事故，本研究定义该状态为预警状态；随着仿真的不断演化，一旦电网的局面评估值超过3，则系统进入危险状态，此时电网濒临或已经发生停电事故。因此将电网运行的风险等级分为三级，如表4所示。

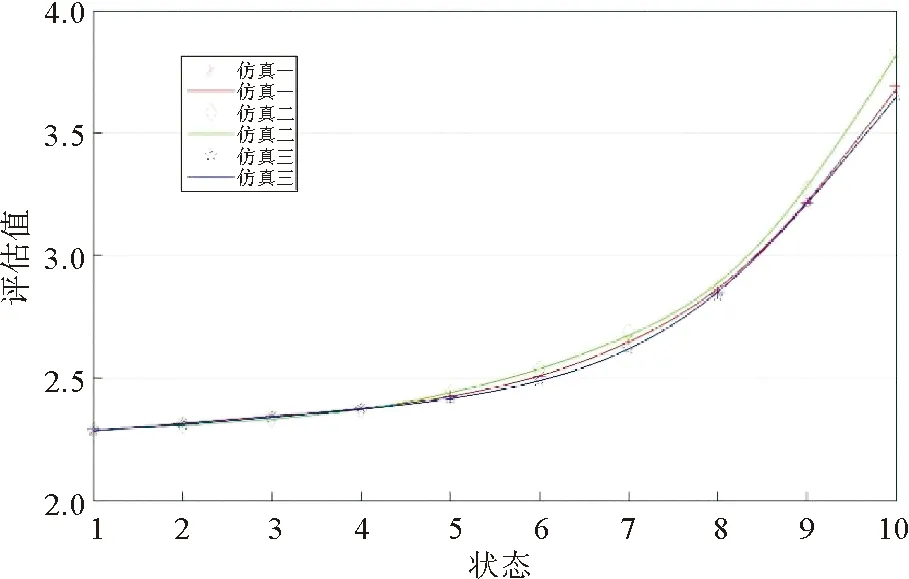
图4 多次仿真过程中电网局面评估函数值变化曲线

表4 电网运行风险等级表

3.2 局面评估函数有效性检验

负荷是电网中主要且易变的变量，对连锁故障的发生有重要影响。电力系统中线路过载所造成的跳闸是连锁故障的主要表现形式，因此利用电网运行中线路负载率来描述系统当前所处状态，同时验证局面评估函数的有效性。定义线路的负载率

(22)

式中：Plmax为系统中线路l的极限传输功率；Pl为系统中线路l当前运行时的有功潮流。

电力系统的运行是复杂多变的，从调度人员的角度考虑，最为关注的是系统在不同时刻的运行状态下是否存在发生大停电事故的可能性。作为判断电网安全运行的局面评估函数，其判断的准确性就显得尤为重要。因此，为了验证本研究所提方法的有效性，在3.1节的仿真过程中，每增加一次扰动，就利用式(22)计算出各条线路的负载率并按照从大到小的顺序排列起来，然后通过最小二乘法拟合后将负载率分布曲线绘制在双对数坐标图中。随着扰动的增加，观察负载率分布曲线的变化情况。

选择仿真过程中不同时期的四次负载率曲线如图5所示。图5(a)～5(d)标出了不同时期相应的负载率分布曲线斜率k及局面评估函数值E(t)。

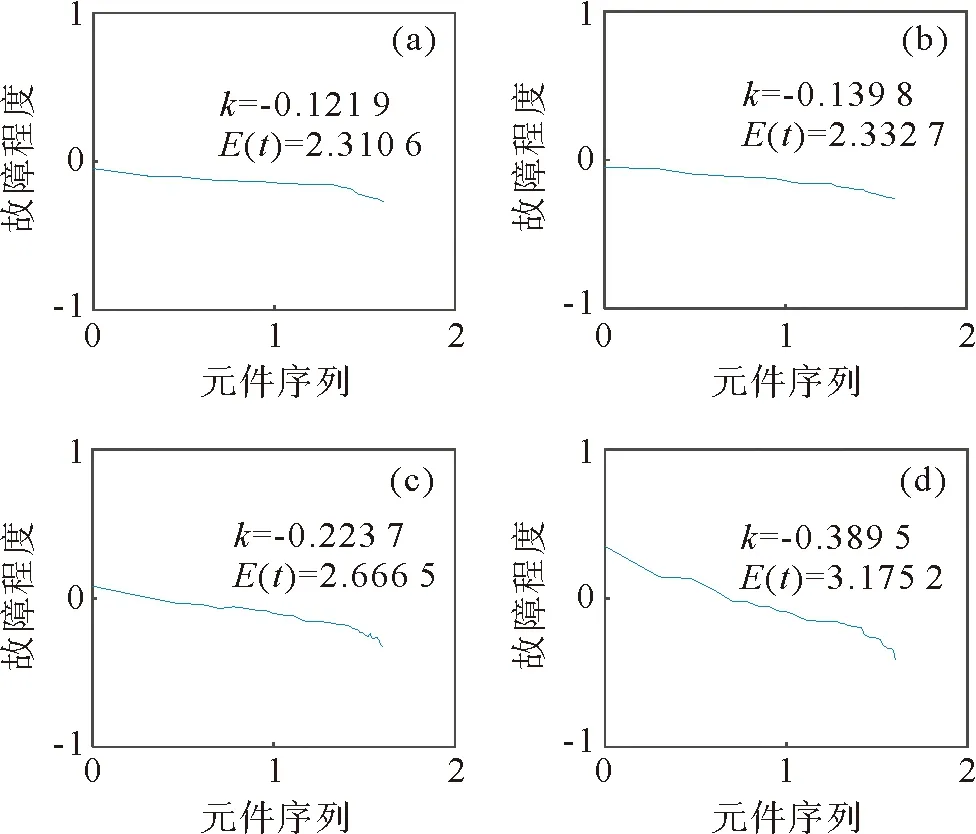
图5 仿真过程中电网线路负载率变化曲线

初始状态时，取系统负载率为0.7，则分布曲线的斜率k=0。随着仿真迭代次数的增加，系统不断受到扰动，负载率分布曲线斜率k的绝对值不断增大但幅度较小。当局面评估函数值为E(t)=2.310 6和E(t)=2.332 7时，系统运行在安全状态，如图5(a)和图5(b)所示，分别对应于图3中A点和B点。电网中可能会出现过载现象，但不会造成大停电事故，此时系统运行在预警状态。当局面评估函数值为E(t)=2.666 5时，如图5(c)所示，对应于图3中C点。过载元件切除后，系统负载率继续增大，分布曲线斜率的绝对值也不断增大，且变化更为显著。图5(d)所示为系统中多条线路出现过载时，局面评估函数值为E(t)=3.175 2，此时系统运行在危险状态，对应于图3中D点。当过载的元件切除后，大停电事故发生，一次事故的演化过程结束。通过仿真演化过程中负载率分布曲线的变化可以看出，系统的演变是符合实际情况的，同时也说明本研究构建的局面评估函数的有效性。

由于电网线路负载率分布越均匀，其抵御各种不确定性冲击的能力越强[21]，因此可以根据负载率的分布得到系统的运行情况。因此，将IEEE39节点系统图放于直角坐标系中(如图1所示)，利用Lowess拟合法[22]，将图5所示线路的负载率利用三维图的形式表现出来(如图6所示)，以便于直观地表示图5所示的运行状态。其中，x轴与y轴确定IEEE39节点系统图中各线路的相对位置，z轴表示拟合后的线路负载率。

图6 仿真过程中电网线路负载率分布图

图6(a)～6(d)分别对应图5(a)～5(d)运行状态下拟合后的线路负载率分布情况。通过对比可以看到，图6(a)和图6(b)中线路负载率的分布相对较均匀，符合图5(a)和图5(b)所示系统运行在安全状态的结论；而对于图6(c)，线路负载率已经出现分布不均现象，部分线路的负载率可能会出现过载，故系统运行在预警状态，与图5(c)所示状态吻合；当系统演化到图5(d)时，系统中多条线路出现过载，且图6(d)中线路负载率分布极其不均匀，系统处于危险状态。图5线路负载率变化曲线与图6线路负载率分布相互对应，反映了符合实际情况的系统演变过程，共同验证了本研究构建的局面评估函数是有效的。

4 HN电网实例分析

采用HN电网电压等级为525 kV以上的节点进行实例分析，其地理接线图如图7所示。

图7 HN电网系统图

初始状态下随机选取10个节点，各个指标归一化后的熵值如表5所示。

表5 各指标归一化后的熵值

应用前文所述的权重计算方法，得到HN电网不同指标的权重值如表6所示。

表6 各指标权重值

利用熵权法分配权重后使用局面评估函数进行系统安全性评估，由于在HN电网中电压等级为525 kV的节点占据主导地位，则Vs=525 kV。利用式(17)计算该状态下系统的局面评估值E(t)=2.343 2。根据表4中的电网运行风险等级划分可以判断，此时系统运行在安全状态。

利用上述方法，在仿真过程中等间距选取10次评估结果，所得评估值如表7所示。根据表7可得局面评估函数值拟合曲线，如图8所示。

表7 仿真过程中HN电网局面评估函数值

由图8可以看到，使用局面评估函数对HN电网进行评估时所得曲线与IEEE39节点系统所得曲线相似，同时满足表4的电网运行风险等级。因此，所得结果符合实际电网的运行情况。

图8 仿真过程中HN电网局面评估函数值变化曲线

5 结论

本研究基于熵理论，从系统的结构特性和实际运行特征出发，统筹考虑网络结构熵、有功裕度熵和电压裕度熵三种指标，提出一种通过构建局面评估函数来评估电网运行状态的方法。利用该评估函数对IEEE39节点系统进行仿真与评估，可以得到各种局面下电网运行状态的评估值，并根据评估值的变化曲线划分电网运行的风险等级。同时，通过仿真过程中产生的线路负载率验证了局面评估函数的有效性。最后，将本研究定义的局面评估函数应用到实际的HN电网中，所得结果符合电网的实际运行情况，对电网的安全运行具有借鉴意义。