基于改进型非奇异终端滑模控制的光伏 MPPT实现*

何 宁 肖文勋

(华南理工大学电力学院 广州 510641)

1 引言

在全球能源紧张、碳排放和环境污染问题等严峻背景之下，大力发展光伏、风力、水力等可再生能源发电技术，实现传统能源向可再生能源的过渡，是中国乃至全球实现“双碳”与绿色可持续发展目标的重要途径。然而，光伏发电具有随机性和间歇性，光伏阵列的输出功率受到外界环境和负载的影响[1]。为提高光伏发电系统的效率，设计合适的最大功率点跟踪(Maximum power point tracking，MPPT)控制方法显得至关重要。经典控制方法主要有扰动观察法[2]和电导增量法[3]等，但存在振荡和误判等问题。随着现代控制理论的发展，基于智能算法的MPPT控制策略被相继提出，例如模糊控制[4]、遗传算法控制[5]、神经网络控制[6]等。这些控制算法可以精确寻找最大功率点，提高系统的鲁棒性，但同时也存在算法原理复杂、内存消耗大、成本昂贵等不足。

滑模控制凭借控制原理简单、大信号稳定、鲁棒性强等优势[7]吸引了众多学者的关注，已有大量的文献将滑模控制技术应用至光伏MPPT方案中。文献[8]和文献[9]根据光伏电池的输出特性设计切换面，得到的仿真结果与扰动观察法进行对比，具有稳态精度高等优势。文献[10]则将最大功率点连线近似为一条直线，并设计光伏电压和电流的线性函数作为滑模面。虽然控制方法简单，但实际上光伏电池输出特性曲线的最大功率点连线并非一条理想直线。文献[11]结合变步长电导增量法和传统线性滑模控制算法，可有效缩短动态调节时间，降低稳态抖振幅度。针对滑模控制在稳态容易出现的抖振现象[7]，文献[12]提出一种基于超螺旋二阶滑模控制的MPPT实现方法，并设计了一种简单无抖振控制器，具有良好的控制效果。

研究表明，传统线性滑模控制在收敛时间和动态特性上都不是最优，为此，将终端滑模控制应用至光伏MPPT中可改善系统向平衡状态收敛速度，并且可在有限的时间内到达平衡点[13]。文献[14]设计了基于光伏电压误差的非奇异终端滑模双环控制，与PI控制系统相比功率提取增加了10%。但该算法需要一个不确定性的上限，并且必须在鲁棒性和抖振效应之间进行折衷。文献[15]则设计基于功率误差的终端滑模控制器，使单相光伏并网系统具有更低的谐波含量，但控制器的计算量较大。文 献[16]则选取光伏输出电流设计终端滑模控制器，虽然控制效果比传统方法优异，但没有考虑到滑模控制律趋于无穷大导致系统进入奇异区域的问题，同时没有详细说明参数的选取。现如今，终端滑模控制在风力发电和电机驱动应用比较广泛[17]，但在光伏发电系统中仍有待继续深入研究。

本文提出了一种基于改进型非奇异终端滑模控制的MPPT实现方法，并以独立光伏发电系统为研究对象进行单峰MPPT验证。在分析了独立光伏发电系统特性后，针对传统终端滑模控制的奇异问题，设计了改进型非奇异终端滑模切换面。为降低控制系统的复杂程度，简化了非奇异终端滑模控制律并验证了系统的稳定性。仿真和试验结果表明，本文所提方法能够获得更快的响应速度，更高的跟踪精度和更大的功率输出。

2 光伏系统模型特性

独立光伏发电系统不与公共大电网相连，只满足小范围内电力的供应，适用于电网较难覆盖的偏远山区、海岛、高原等地区[1]。图1为独立光伏发电系统结构图，系统由光伏阵列、Boost变换器、控制器以及负载组成。

图1 独立光伏发电系统结构图

2.1 光伏电池模型

光伏电池利用光伏效应直接把太阳能转化为电能，保证了光伏发电的实时性和高效性。多个光伏电池单体组成光伏组件，光伏组件通过串并联方式组成光伏阵列。根据文献[2]建立的光伏电池模型，求解光伏电池输出电流Ipv为

式中，Isc为光生电流；Ido为无光照时二极管的反向饱和电流；q为电子电荷；K为玻尔兹曼常数；A为常数因子；Rs为串联电阻；Rp为旁漏电阻。由于光伏电池的串联电阻很小，并联电阻很大，在实际工程中可忽略不计。因此，光伏输出电流可简化为

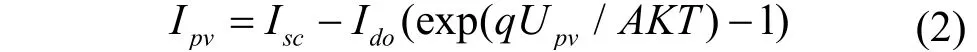
根据式(2)可求解光伏电池的输出功率Ppv为

由式(2)和式(3)可知，光伏电池的输出电压和电流之间具有典型的非线性输出特性，并且当外界环境变化时，光伏电池的输出特性也将发生变化。MPPT控制方案的设计正是结合光伏电池输出功率与电压、电流的关系，不断调整步长并最终达到最大功率点。

2.2 Boost变换器模型

图1所示的Boost变换器由电感L、功率开关管VT、二极管VD以及输出电容C2组成，变换器的输入端接入前置电容C1以提供瞬态的电流需求，同时作为滤波电容吸收影响电感电流的开关纹波。当系统处于稳态且电感电流连续时，光伏阵列的输出电流Ipv可近似认为与电感电流IL相等。定义α为功率开关管的离散控制输入，当系统开关频率足够高并且纹波很小时，可以将离散输入考虑为占空比。因此，定义系统的状态变量为x=(x1x2)T=(IL Uo)T，采用非线性滑模控制理论描述Boost变换器的状态空间平均模型可得一般性表达式为

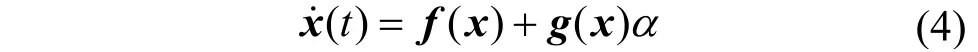
式中，α为控制信号输入，亦为PWM占空比值。式(4)中各项参数计算可得

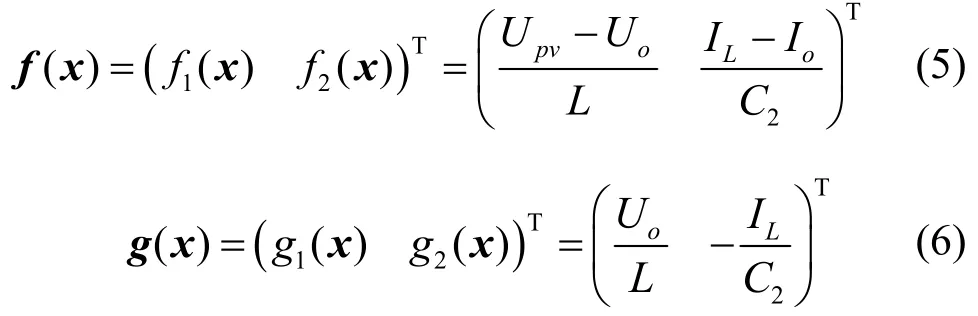
3 MPPT控制系统设计

根据电路最大功率原理，通过调节Boost变换器的占空比使光伏阵列输出阻抗和变换器输入阻抗相匹配，从而实现最大功率点跟踪。图2为所设计的MPPT控制方案，该方案由内、外环两部分构成。外环通过检测光伏阵列的输出电压和输出电流，采用电导增量法获取参考电流Iref；参考电流与电感电流的误差作为内环控制器的输入，构成改进型非奇异终端滑模切换面。根据非奇异终端滑模控制原理求取系统控制律，并结合实际工况改变占空比大小，进而实现光伏MPPT控制。

图2 MPPT控制方案逻辑框图

3.1 电导增量法设计

电导增量法可根据光伏阵列输出功率和输出电流的关系曲线，对输出电流Ipv求微分后得到。由于数字控制检测及控制精度的限制，以ΔPpv/ΔIpv近似代替微分运算后可得到

式中，ΔIpv为扰动电流步长；ΔUpv为变化的光伏电压。

在固定环境条件下，光伏阵列的输出功率和电流是以最大功率点为极值的单峰二阶可导函数，如图3所示。在最大功率点处满足控制要求，此时不需要进行扰动，对应的输出电流即为参考电流。而在其他情况下，无论工作点处于曲线上的哪一点，它们都将通过改变扰动步长逐步朝最高点靠近。

图3 电导增量法原理图

3.2 非奇异终端滑模控制器设计

传统终端滑模控制在光伏MPPT控制过程中出现的奇异问题，会直接影响系统控制器设计以及控制效果。奇异问题指滑模控制律趋于无穷大，存在不连续或不可导的情况，系统进入奇异区域[18]。在现有研究基础之上，针对非线性二阶系统设计的非奇异终端滑模切换面为

式中，p＞q＞0且p、q都为正奇数，β＞0。符号函数sgn()的引入是为了解决当x2≤0时控制表达式出现的奇异问题。当x2=0时，式(8)中非线性函数部分为0且整个表达式也为0，此时系统到达滑模面。因此，改进后的表达式可使非线性函数部分有意义。

所设计控制方案应快速达到最大功率点并且在稳态时应尽量减少误差，同时在受到外界环境干扰或者系统内部不确定因素影响时，也要保持良好控制效果。改进型非奇异终端滑模控制是一种有效的控制方法，主要包括滑模面设计、控制律计算以及稳定性分析。当光伏发电系统运行于最大功率点时，滑模控制系统到达滑模面，此时满足IL-Iref=0。定义x1为电感电流误差积分，然后分别求其一阶、二阶导数后可得到

非奇异终端滑模控制系统可在有限的时间内到达平衡点，根据系统状态不同的运动阶段，有限时间由到达时间和调整时间组成[13]。根据文献[14]推导可知，非奇异终端滑模控制的到达时间与传统终端滑模控制相同。定义系统任意初始状态到滑模面s=0的时间为tr，当t=tr时，满足s(tr)=0并且≤η|s|，因此可计算到达时间tr为

式中，η＞0。

当系统状态处于滑模面上时，调整时间ts可计算为

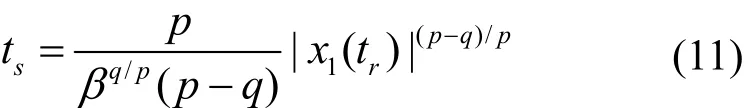
滑模控制律由等效控制律αeq和切换控制律αsw构成[14]，前者作用于滑动阶段，后者作用于到达阶段。为提高系统的动态响应速度和稳态精度，选取式(12)指数趋近律作为切换控制

式中，ε＞0，k＞0。为防止出现较大抖振，ε的取值一般较小。

对非奇异终端滑模表达式(8)求一阶导数并将式(4)、式(9)和式(12)代入其中可求解系统的整体控制律α为

下面利用Lyapunov第二法证明，对于式(4)系统，所设计的切换面式(8)和简化后的滑模控制律式(14)，系统满足可达性和稳定性要求。因此，选择如下Lyapunov函数

式(15)对时间进行求导后，代入式(8)和式(14)后得到

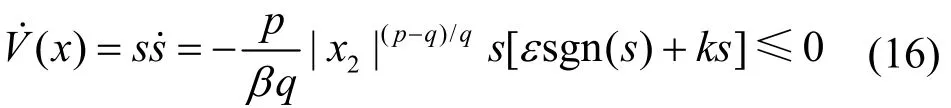
从式(16)中可以看出，由于p＞q＞0且为正奇数，p-q为偶数，0＜(p-q)/q＜1。当x2≠0时，|x2|(p-q)/q＞0恒成立；当x2=0时，式(16)为0。因此，所设计的控制律满足Lyapunov稳定性条件。

此外，为研究外部干扰和参数不确定性对系统控制器的影响，将式(4)修正为

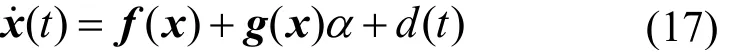
式中，d(t)表示所有不确定性干扰且满足|d(t)|≤lg，lg＞0。选取相同的Lyapunov函数求导之后，可得到与式(16)相同的表达式。由此可见，所设计的改进型非奇异终端滑模控制是一种鲁棒性强的控制方法。综合所有分析可知，所提出的非奇异终端滑模切换面和简化的控制律满足Lyapunov稳定性条件，跟踪误差可在有限时间内收敛至零，系统满足稳定性要求。

4 特性分析

4.1 仿真分析

在理论分析和控制器设计的基础上，为了验证所提控制方法的可行性，首先在Matlab/Simulink中搭建了独立光伏发电系统模型，光伏阵列由5块TrinaSolarTSM-220PA05光伏面板串联而成，系统参数如表1所示。所设计的电导增量法将每一步的增量值ΔI设定为0.001 A，以确定参考电流Iref。为加快系统动态响应速度和减小稳态误差，结合目前对终端滑模控制系数的研究，通过进行一系列比较试验[20]后，最终确定合适的非奇异终端滑模控制器参数如下：β=1 000，p=5，q=3，ε=0.001，k=800。由于滑模控制中的开关控制信号普遍存在切换频率不固定的问题，容易引起系统的抖振，因此将控制信号与三角波进行比较后产生频率固定的PWM脉冲，减小系统抖振，增加系统稳定性。

表1 光伏发电系统参数

首先讨论标准环境条件下，系统启动时的最大功率点跟踪特性。设置仿真条件如下：温度25 ℃、光照强度为1 000 W/m2，仿真时间0.2 s。图4为系统启动时MPPT特性曲线图，可以看出系统约在80 ms内达到最大功率点，具有非常快的响应速度。稳态时光伏系统输出的最大功率稳态平均值约为1 102.6 W，与光伏阵列标称值的偏差很小，表明所提方法能很好地跟踪最大功率点，在稳态精度方面具有优势。

图4 系统启动时MPPT特性

其次讨论光照强度变化下最大功率点跟踪的效果。设置仿真条件如下：温度25 ℃，仿真时间为2 s，在1 s时光照强度从1 000 W/m2降至700 W/m2。为了验证所提控制方法的优越性，保持光伏阵列规格、Boost变换器模型、负载以及仿真环境相同，采用不同的控制方法进行对比分析：传统电导增量法[3]、传统滑模控制法[8]、基于电导增量法和滑模控制结合法[11]、传统终端滑模控制法[16]以及本文所提非奇异终端滑模控制法。图5为光伏阵列输出功率随光照强度变化的曲线对比图。从图5中可以看出，当温度不变而光照强度降低时，光伏阵列的最大功率点降低并且幅度很大，这也说明光照强度对最大功率点的影响较大。对比五种控制方法的仿真结果可知，传统电导增量法虽然控制简单，但输出功率在稳态时振荡较大。传统滑模控制法的启动特性较慢，需要较长时间才能达到稳态，并且条件改变时暂态切换时间较长。而基于线性滑模切换面的电导增量法则具有优异的响应时间和跟踪特性，但无法避免滑模控制本身性质所造成的抖振和超调。本文所提的控制方法的启动响应速度是最快的，并且在到达最大功率点时能保持稳定，整体无波动、无误跟踪。

图5 光伏阵列输出功率对比图

表2为五种控制方法的对比仿真数据，其中Pavr为实际功率平均值，ΔP为与参考功率的误差值，t1为系统启动至最大功率点的时间，t2为光照强度变化时重新达到稳态的时间。从表2中可以看出，本文所提方法的稳态波动值小，启动时间和动态切换时间相对较短，整体控制效果具有极大的优势。

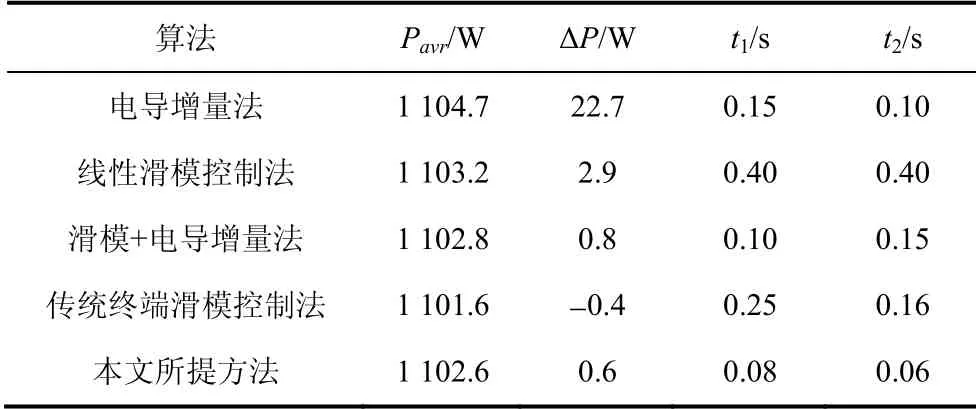
表2 五种控制方法仿真对比数据

另外，当光照强度从1 000 W/m2降至700 W/m2，五种方法均呈现出波动，但电导增量法在转换瞬间出现如图6a所示的误判和振荡行为，具有不稳定性。图6b为采用本文改进型非奇异终端滑模控制法得到的P-V仿真结果，由图6b可知振荡和误判的程度极大减少，具有较好的鲁棒性。

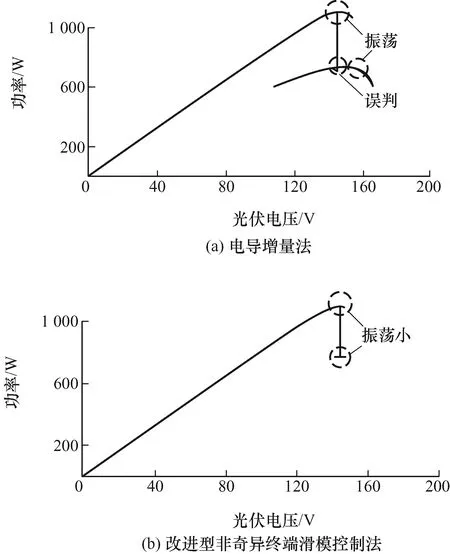
图6 P-V曲线仿真结果对比图

4.2 试验分析

为验证所提方案的可行性，搭建了如图7所示功率为1.1 kW的试验平台，该平台由Chroma 62150H-1000S直流电源、Boost升压电路、直流电子负载和DSP28335控制系统组成。可编程光伏模拟电源工作于“SAS_MODE”模式。MOSFET选用英飞凌IPW65R019C7，开关频率为20 kHz；二极管选用SiC FFSH2065A；直流电子负载工作于定电阻模式；主电路其他参数与仿真参数相同，如表1所示。试验内容如下所示：固定光照强度和温度、光照强度变化和温度变化，然后观察光伏电流Ipv、光伏电压Upv以及变换器输出电压Uo的变化过程。

图7 试验平台

首先，稳态条件25 ℃、1 000 W/m2下的试验结果如图8所示。图8a表明系统在最大功率点的光伏电流为7.56 A，光伏电压为146 V左右，电流和电压的波形略有波动。图8b为变换器的输出电压Uo，可知系统在稳态情况下误差小。

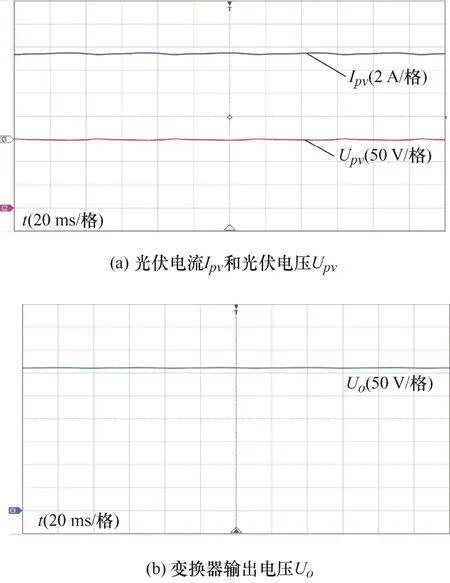
图8 稳态试验结果

其次，观察光照强度的改变对光伏发电系统的影响。保持温度不变，光照强度从1 000 W/m2变化为500 W/m2瞬间，图9a中光伏电流波形突变较大，但又重新到达稳态，动态切换时间为180 ms，稳态电流波动小。图9b表明随着环境的改变，通过改变Boost变换器的占空比，输出电压也改变，从而跟踪最大功率点，保证光伏阵列提供最大功率。

图9 光照强度变化动态试验结果

最后，观察温度的改变对光伏发电系统的影响。保持光照强度不变，模拟温度从45 ℃变为10 ℃，随后从10 ℃变为45 ℃，得到图10所示的系统动态响应曲线。同理分析可得，条件变化时的动态响应时间约为40 ms，温度变化瞬间光伏电流和输出电压的变化幅度比较小，远不如光照强度的影响大，这与光伏阵列的输出特性相符。

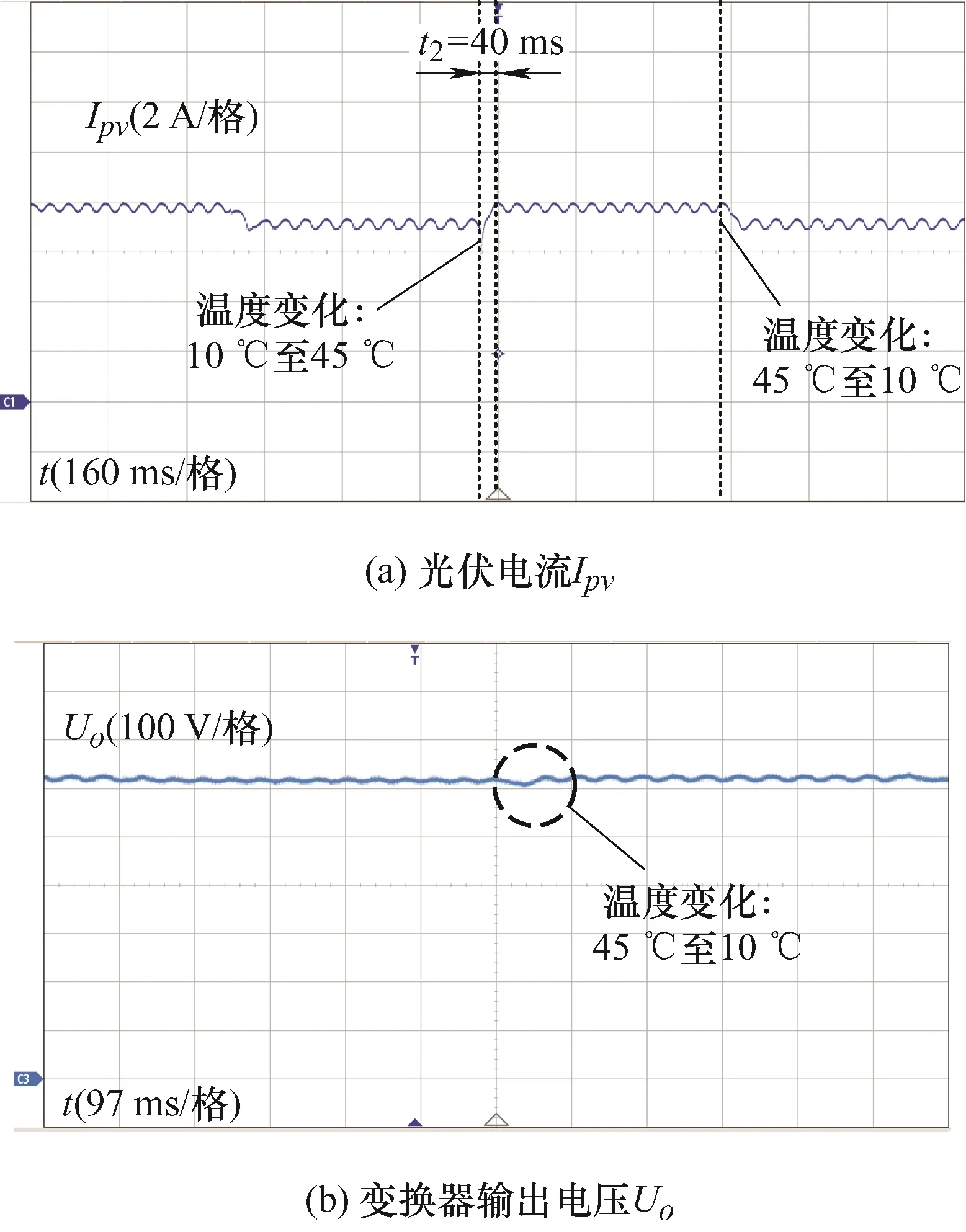
图10 温度变化动态试验结果

5 结论

针对传统滑模控制MPPT方法存在响应速度较慢和抖振较大等不足，提出了一种基于改进型非奇异终端滑模控制的实现方法。该方法通过结合电导增量法与改进型非奇异终端滑模控制器，极大提升了独立光伏发电系统中单峰MPPT的控制性能。仿真与试验结果均表明，与传统控制方法相比，本文所提的控制方法具有以下特点。

(1) 具有更好的响应速度和稳态精度，系统可以在有限的时间内到达最大功率点。

(2) 保持快速响应的前提下，简化后的控制律便于控制器的设计，解决了传统终端滑模控制器的奇异问题，具有可行性。

(3) 外界环境发生变化时，系统的动态特性优于传统控制算法，具有较强的鲁棒性。