计及流-热耦合热网络模型的IGBT结温计算*

许智亮 葛兴来 李 金 柯倩霞 朱 丹

(1. 西南交通大学电气工程学院 成都 611756； 2. 中车大连机车车辆有限公司 大连 116022)

1 引言

绝缘栅双极型晶体管(Insulated gate bipolar transistor，IGBT)因其高效的电能转换效率被广泛应用于轨道交通、新能源发电和电动汽车等领域[1-2]，广泛的应用工况对IGBT模块的可靠性提出了更高的要求。相关工业统计表明，温度因素是造成功率器件失效的主要原因[3]，包括最高结温、平均结温、基板壳温和散热器温度在内的温度因素会对IGBT模块的损耗计算、剩余寿命和可靠性评估产生重要影响[4-5]。因此，IGBT模块的结温计算对于保障电力电子变换器的可靠运行具有重要意义。

IGBT模块的结温计算方法大致可分为直接测量法、热敏电参数法和热网络法[6]。其中，直接测量法主要利用热敏元件或者红外成像设备对IGBT模块进行结温监测，通常受限于模块类型或需要破坏模块封装完整性[7]。热敏电参数法通过离线校正模块电参数与结温的映射关系，并以此监测结温，但是多数热敏电参数不易在实际器件高速开关的工况中获取[8]。热网络法根据模块数据手册或是对实际IGBT模块进行有限元仿真，提取热网络参数，然后根据实际温度参考点计算IGBT结温[9]，在电气化交通领域具有较好的应用前景。

目前国内外关于利用热网络法进行IGBT结温计算已有大量研究[10-13]。其中，文献[10]利用IGBT模块的数据手册拟合得到器件热网络模型，用以计算牵引变流器中的IGBT结温，但是数据手册中的热网络数据与实际器件具有一定误差。进一步，文献[11-12]对IGBT模块进行有限元分析(Finite element analysis，FEA)，同时考虑模块内各芯片自热和耦合热阻抗，提取更精准的热网络参数。文献[13]更加深入地考虑实际工况中的IGBT全桥模块的热耦合作用，利用FEA评估了芯片之间、芯片与桥臂以及相与相之间的热耦合作用，但是缺乏对散热条件的考虑。为此，文献[14]单独考虑散热器与环境的对流热阻，利用小波包变换和马尔科夫链对对流热阻实现随机模拟，并将对流热阻与实际器件损耗匹配。然而利用统计学方法模拟得到对流热阻依赖于算法准确性，未曾从实际传热过程中的热耦合进行考虑。尽管热网络法结温监测已考虑热耦合效应和散热器条件，但是与真实模拟模块内热耦合以及模块与散热器热耦合仍存在一定差距。

综上，本文在已有研究的基础上，利用考虑IGBT模块与散热器之间传热影响的有限元仿真，提出一种计及流-热耦合的热网络模型的IGBT结温计算方法。第2节对1 200 V/50 A模块及相应水冷散热器进行有限元仿真，考虑流体与温度场耦合对IGBT结温的影响，分别提取IGBT模块的热网络模型和计及流-热耦合的IGBT模块和散热器热网络模型。第3节搭建功率循环试验平台，提取壳温及散热器水温分别代入热网络模型计算结温，并与试验结温对比验证。结果表明，所提方法计算所得IGBT结温更贴近真实结温，且更易于实际应用。

2 有限元仿真和热网络模型搭建

2.1 IGBT模块及散热器

本文用以仿真及实物验证的IGBT模块选用Infineon公司焊接型模块FF50R12RT4，该模块在中小功率场合应用较广，其封装内部结构和纵向结构示意如图1和图2所示。

图1 IGBT模块实物内部结构图

图2 IGBT模块纵向结构示意图

为了简化封装模块的结构，本文忽略了封装外壳、电气端子、绝缘硅胶和键合线。IGBT模块封装结构中各层材料的三维尺寸根据实际测量及Infineon公司提供的数据手册[15]得到，IGBT模块各层三维尺寸参数及材料特性如表1和表2所示。

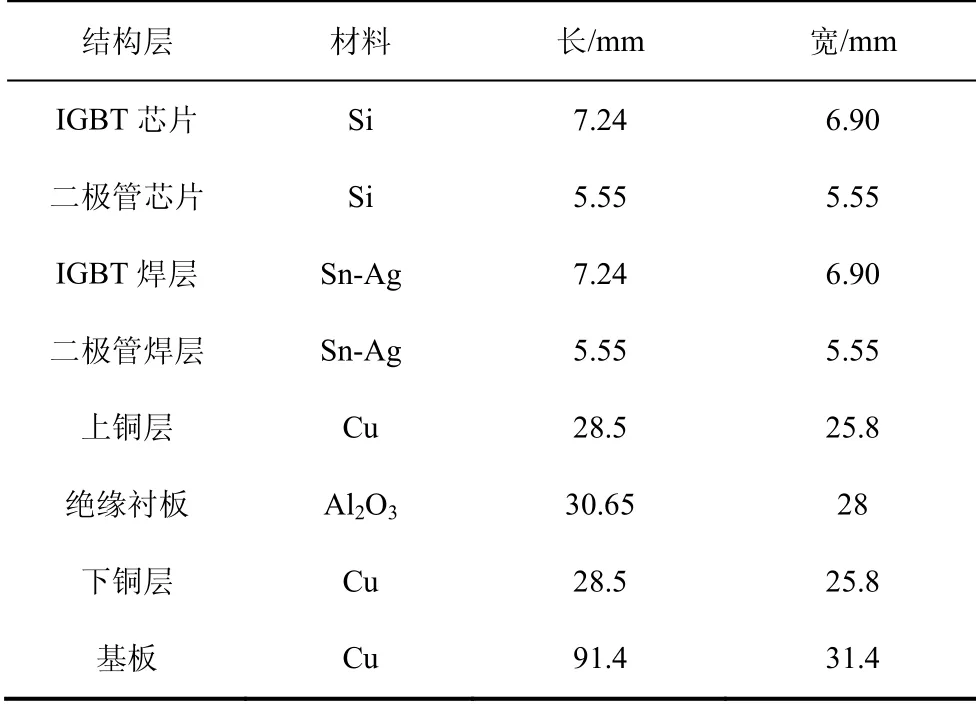
表1 IGBT模块三维尺寸参数

表2 IGBT模块及散热器的材料特性

散热器采用水冷强迫对流散热，根据IGBT模块尺寸设计容纳两个IGBT模块的Al材料散热器，Al材料的相关特性如表2所示，散热器尺寸为125 mm×125 mm×25 mm，内部水道设计为10 mm水道，水冷散热器具体结构如图3所示。

图3 水冷散热器的结构示意图

2.2 有限元仿真

根据IGBT模块与散热器的结构及三维尺寸，利用有限元仿真软件ANSYS Workbench搭建IGBT及散热器的三维有限元模型。其中IGBT模块及散热器的网格划分选用Mechanical选项，折中考虑仿真精度与仿真时间成本，本文在IGBT芯片等对仿真结果影响较大的部分采用精细化密集网格划分，在模块其他部分采用较粗略的扫掠式网格划分，流道及流体采用CFD物理选项进行网格划分，网格划分的结果如图4所示。

本文分别对IGBT模块进行双向流-热耦合仿真和瞬态热仿真，其中双向流-热耦合仿真为散热器施加1.5 m/s、15 ℃的冷却水，根据数据手册中IGBT的功率损耗及芯片三维尺寸，直接分别为IGBT芯片加载30 A和60 A负载电流下的生成热载荷4.5×109W/m3、9×109W/m3，同时借助Workbench中的System Coupling模块，实现流体仿真与瞬态热仿真之间传热界面数据的双向传输更新。瞬态热仿真中，需要为IGBT模块基板底部设置与实际散热器相当的散热条件。

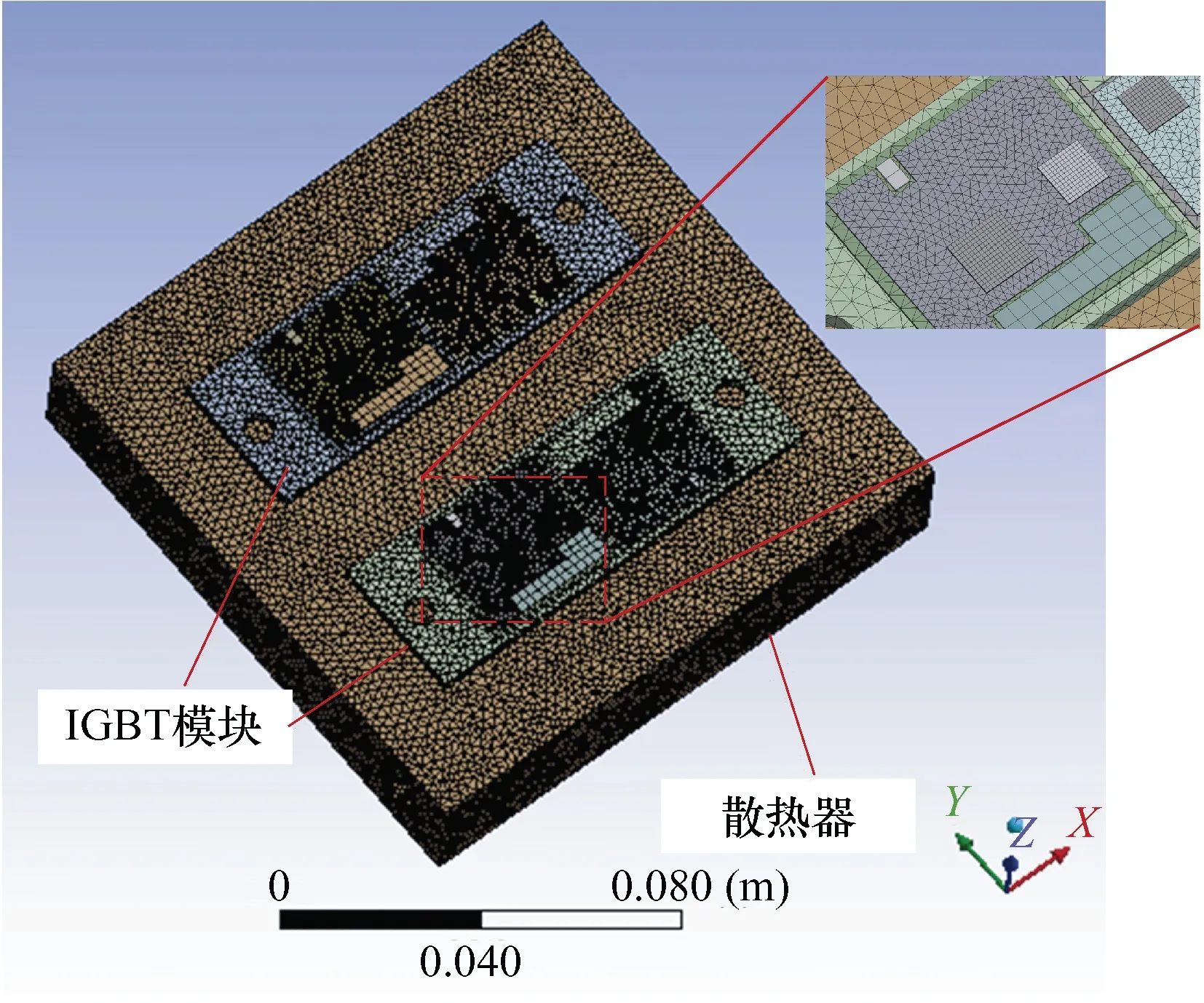
图4 IGBT模块及散热器网格划分结果

对流换热过程中的定性温度tm为

式中，tw为水冷散热基板的平均壁温，参考环境温度设置为25 ℃；tf为冷却水的温度，设置为15 ℃。 根据定性温度tm查阅水物性参数表可知，水的运动黏度υm为1.008 7×10-6m2/s，水的导热系数为λm=0.599 W/(m·K)，普朗特数Prm=7，为了确定管道内的冷却水流体状态，需要计算散热器中冷却水纵掠管道内壁的雷诺数。

式中，v为冷却水流速，根据已选型的水冷机计算得出为1.5 m/s；L为纵掠平壁情况下平壁板长，本文中该参数为散热基板中水道的长度，即100 mm。

在根据工程经验临界雷诺数取Rem=5×105，由于Rem＜5×105且0.6＜Prm＜60，故整个纵掠平壁可均视为层流强迫，纵掠平壁时整个平壁表面的努谢尔数Num计算公式按POHLHAUSEN[16]给出的平均对流换热系数关联式计算

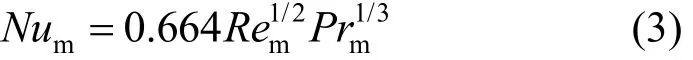
将式(2)和式(3)代入对流换热系数求解公式可得，纵掠平壁时的对流换热系数为

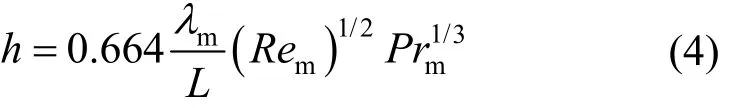
故水冷基板中的冷却水与IGBT基板的对流换热系数h为2 937 W/(m2·K)。因此，在瞬态热仿真中为IGBT基板底部设置3 000 W/m2的对流换热 系数。

IGBT芯片在导通过程中表现为焦耳热效应，因此可将IGBT芯片等效为内热源，根据热力学传热微分方程，可得在有限元仿真软件中模块温度分布求解公式为

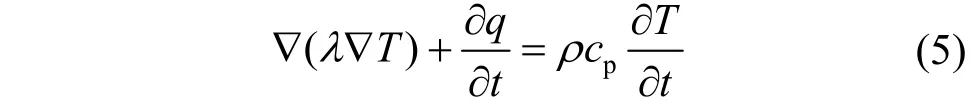
式中，λ为材料热导率；T为模块内部温度；q为热流量；ρ为材料密度；cp为材料热容。

设置仿真时长为5 s，确保IGBT模块结温达到稳态，得到IGBT达到最高结温时的模块温度分布如图5和图6所示。

图5 30 A等效电流下IGBT稳态最高结温时的温度分布

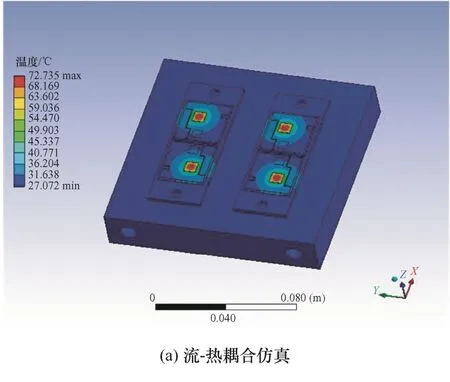
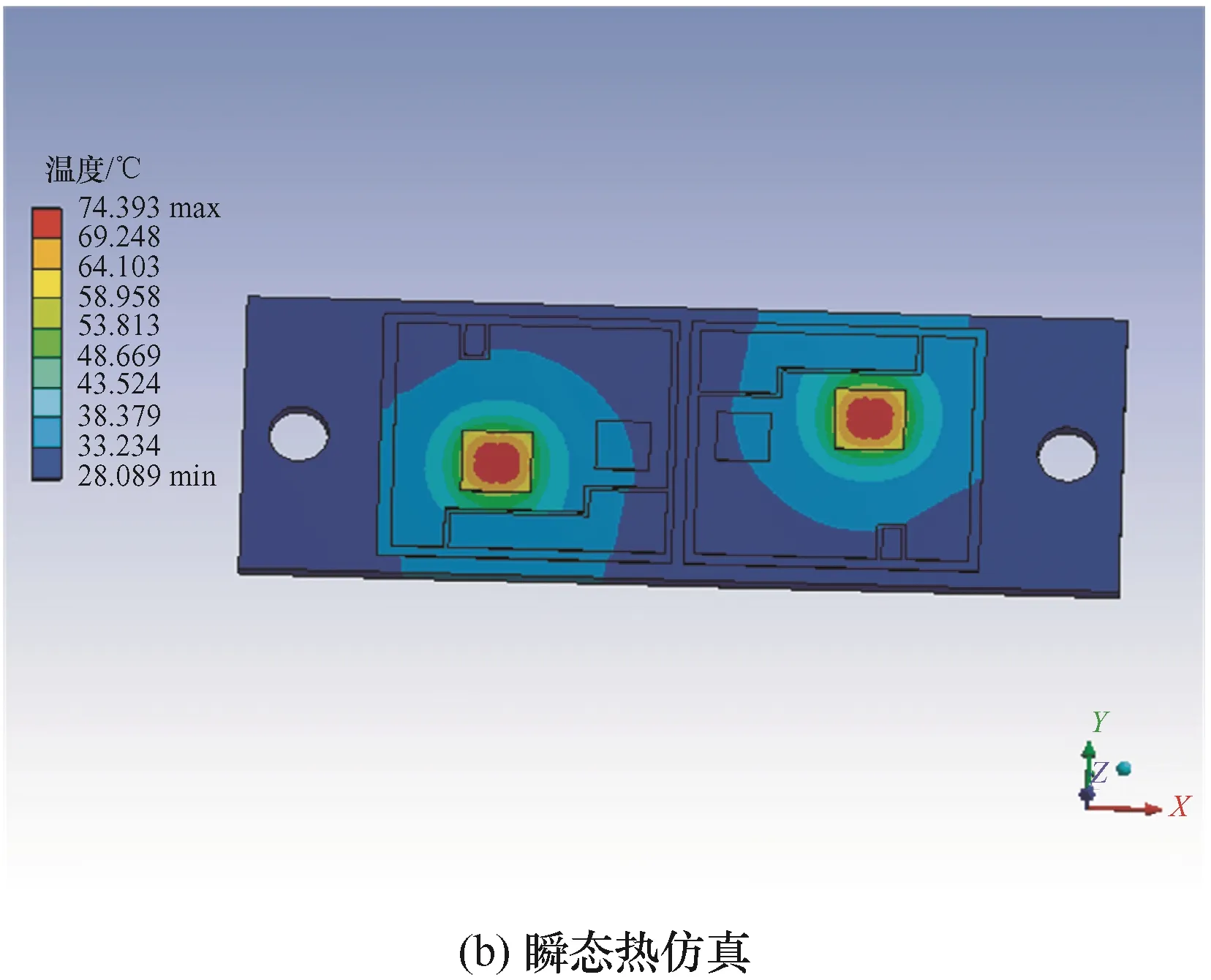
图6 60 A等效电流下IGBT稳态最高结温时的温度分布

根据不同电流等级下的温度分布云图可知，流-热耦合仿真和瞬态热仿真最高结温存在较大差异，根据IGBT模块的加热过程提取模块的升温曲线如图7所示。

图7 流-热耦合仿真与瞬态热仿真中的IGBT模块升温曲线

对比流-热耦合仿真与瞬态热仿真中的升温曲线可知，由于流-热耦合仿真中存在IGBT模块与底部散热器的实时热交换，而瞬态热仿真中将散热条件利用集中参数法等效为一个对流换热系数，缺乏对真实环境的模拟，两种仿真中的IGBT模块升温曲线变化趋势存在较大差异，这将影响提取得到的热网络参数，进而影响结温计算的准确性。

2.3 热网络提取

为了根据壳温或环境温度等易于获取的温度参考点计算结温，需要对IGBT模块或IGBT模块及散热器整体建立热网络模型。

常用的热网络模型有Foster热网络和Cauer热网络模型，相较于需要根据IGBT模块实际结构及各层材料物理参数搭建的Cauer热网络模型，本文选用更易于在实际中应用的四阶Foster热网络模型，Foster热网络模型不具备实际物理意义，根据IGBT模块的温度变化曲线与热网络定义式即可拟合得出，图8为IGBT模块与散热器的热网络模型示意图。

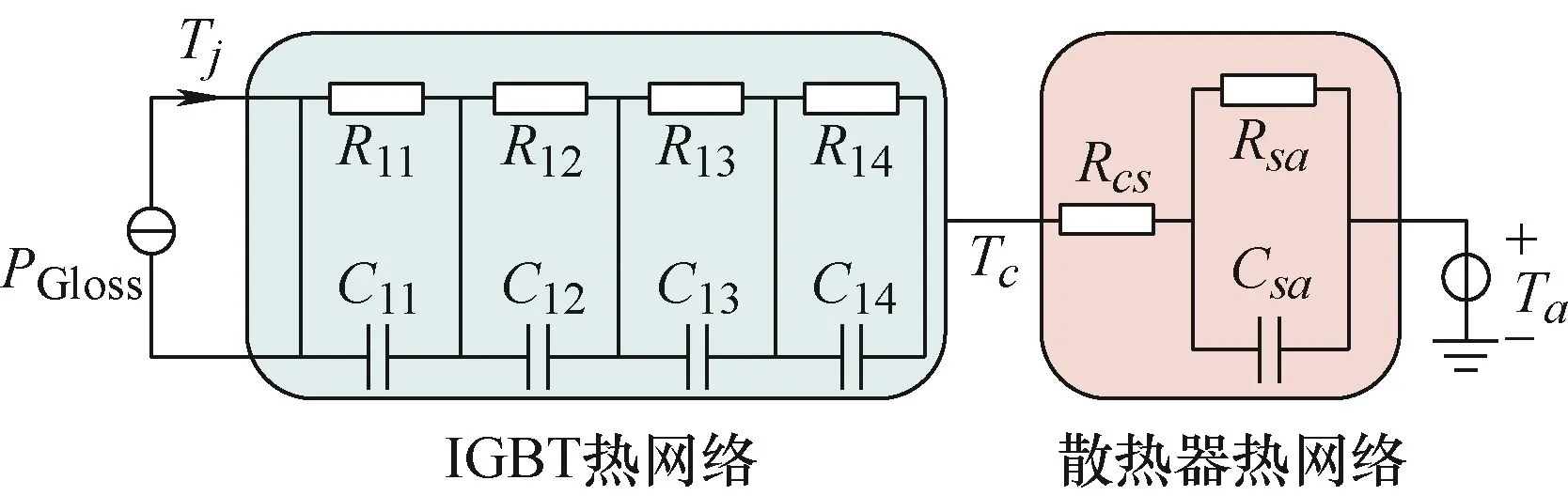
图8 IGBT模块与散热器的Foster热网络模型

通常对IGBT模块与散热器分别建立热网络，但是实际应用中壳温变化数据不易提取，因此本文拟利用散热器中的冷却水温作为温度参考点，在考虑流-热耦合的基础上，建立包含IGBT模块和散热器的四阶热网络模型。四阶热网络模型中热阻抗计算公式如式(6)所示

式中，Zth为热阻抗；Ri为第i阶热阻；Ci为第i阶热容；t为时间变量。

结合第2.2节中提取的IGBT结温升温曲线，同时提取流-热耦合仿真中的冷却水温变化曲线，瞬态热仿真中的壳温变化数据，利用Matlab软件拟合得到流-热耦合仿真和瞬态热仿真中的四阶热网络模型，具体参数如表3所示。

表3 流-热耦合仿真和瞬态热仿真中的热网络模型参数

3 试验验证及结果分析

3.1 加速老化试验平台搭建

本文根据IEC标准(IEC60749-34)搭建直流功率循环加速老化试验平台，试验原理如图9所示。

待测器件(Device under test，DUT)栅极的直流电源产生足够的驱动电压与驱动电流使其开通，加热电流利用陪跑IGBT模块S1控制，当陪跑IGBT模块开通时，较大的加热电流通过待测DUT的IGBT芯片，而后陪跑IGBT模块S1转换为截止状态，进而使待测IGBT模块不再流经负载电流。同时对待测IGBT芯片通入较小的测量微电流(100 mA)，通过测量IGBT芯片的热敏电参数获取IGBT芯片结温。当加热电流断开时，对IGBT芯片进行散热处理，当IGBT芯片下降至指定最低结温时，使陪跑IGBT模块S1再次导通，开始新一轮的结温波动，以此模拟IGBT芯片在实际工作环境中受到的热冲击。

图9 直流功率循环加速老化试验原理

试验平台主电路如图10所示，本文将4个10 Ω/10 kW的小阻值大功率铝壳电阻并联接入主电路，将电压源与电阻串联等效为加热电流源，利用直流电源保持DUT器件恒定导通，在不加负载电流时通入微电流利用小电流下的饱和压降法进行结温监测[17]，基于小电流下的饱和导通压降Vce(T)法结温监测电路原理如图11所示。

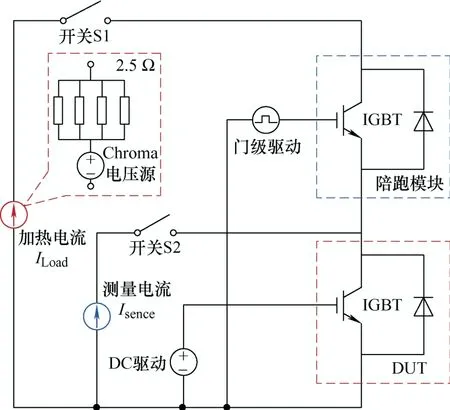
图10 功率循环试验加热主电路示意图

图11 基于Vce(T)法的结温测量电路原理图

当两个二极管D1和D2具有相同的特性时，选择合适的放大器增益时，可利用放大器输出电压Vop表示IGBT饱和导通压降Vce。

加速老化试验平台装置如图12所示，包括可编程直流源Chorma，待测模块FF50R12RT4和陪跑模块FF75R12RT4，工业水冷机和红外测温仪。

图12 加速老化试验平台

3.2 结温波动曲线提取

基于Vce(T)法对IGBT模块进行结温监测时，需要建立IGBT芯片结温Tj与IGBT饱和导通压降Vce之间的线性关系式，故在对IGBT模块进行结温在线监测前，需要对IGBT结温Tj与IGBT饱和通态压降Vce的线性关系进行校正，并拟合得到两者之间的结温系数。对DUT进行离线结温系数校正的试验如图13所示。

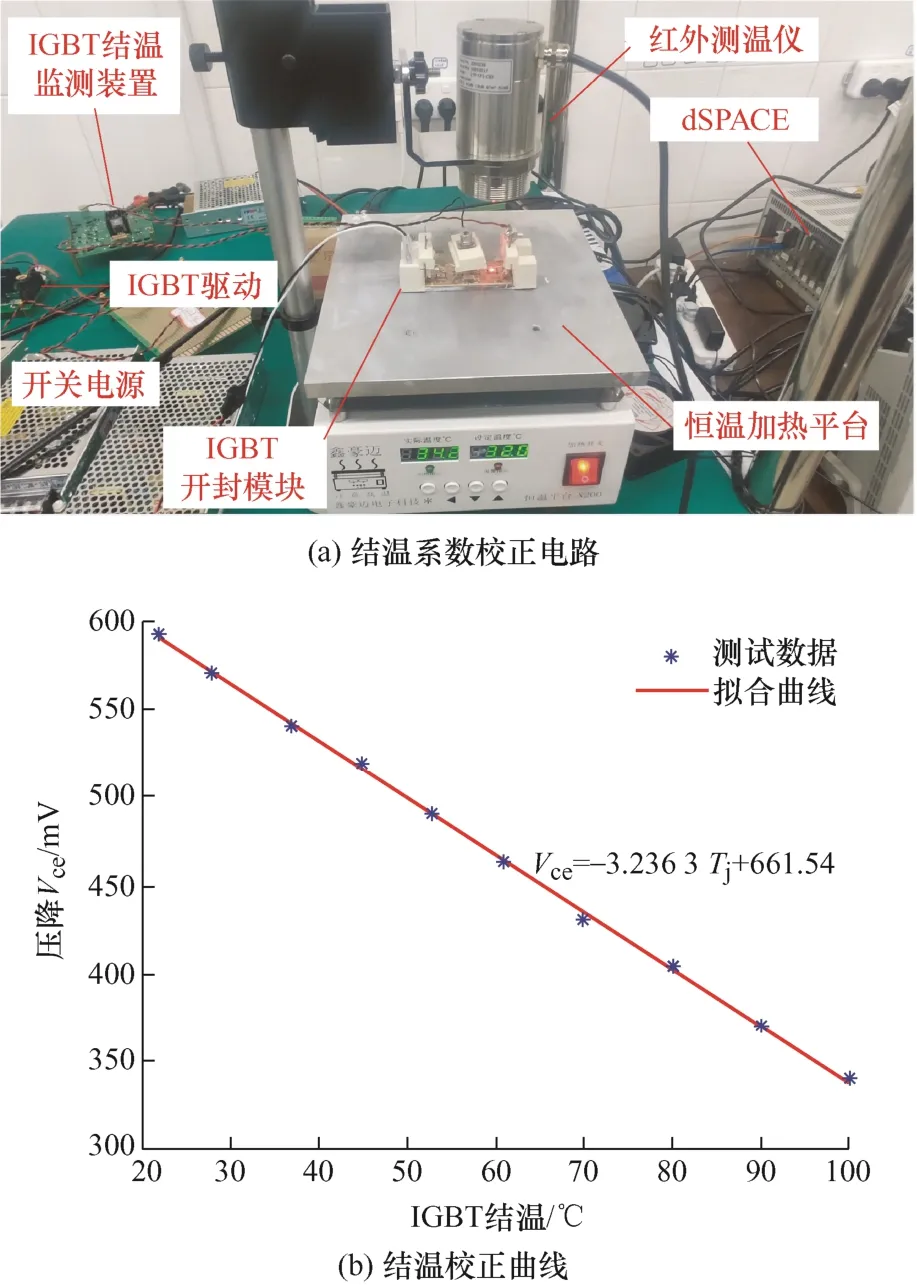
图13 IGBT温度系数校正

本文利用恒温加热平台将IGBT模块加热至指定温度，并利用使IGBT芯片处结温保持稳定，此时IGBT驱动模块输出栅极控制信号，并利用IGBT结温监测电路板为IGBT模块通入100 mA微电流，确保IGBT模块处于开通状态且不会产生较大热损耗对结温测量造成影响，并利用红外测温仪得到IGBT结温，最后利用Matlab软件将IGBT结温与饱和通态压降进行数据拟合，以一阶线性函数为作为拟合函数，拟合得到结温校正曲线，拟合结果表明IGBT结温与饱和导通压降Vce具有较好的线性函数关系。

3.3 热网络法结温计算验证

利用可编程直流源分别输出30 A电流和60 A电流，并分别采集升温阶段5 s内待测IGBT模块的结壳温变化曲线，利用热电偶提取试验平台中IGBT模块的壳温变化曲线，同时与FEA中的壳温变化曲线对比。

由图14可知，试验中的壳温变化曲线与FEA中的相接近，因此将试验中IGBT模块的壳温变化数据输入第2.3节中根据瞬态热仿真所建立的热网络中，同时将散热器水温输入根据流-热耦合建立的热网络中，计算得到IGBT模块的结温变化曲线。

图14 试验中与FEA中IGBT模块的壳温变化曲线

由图15可知，计及流-热耦合的热网络模型计算的结温更接近实物试验结温，基于瞬态热仿真建立的热网络模型的结温计算高于实际结温，这是由于集总参数法等效散热条件时，对真实参数存在一定程度的简化，导致搭建的热网络模型与真实情况存在一定差异。此外，基于瞬态热仿真的热网络模型需要以壳温作为温度参考点进行计算，而计及流-热耦合的热网络模型可以选用散热器内冷却水温作为温度参考点，在电气化交通领域无疑具有更大的应用前景。

图15 流-热耦合与瞬态热仿真热网络结温计算对比

4 结论

为了方便准确地获取IGBT模块结温，本文在传统热网络法的基础上，考虑散热器流体散热效果，提出一种计及流-热耦合的热网络结温计算方法。基于有限元仿真软件实现流-热耦合仿真并提取热网络模型，搭建了功率循环加速老化试验平台，对所提方法与传统方法进行对比验证。对仿真及试验结果分析得到以下结论。

(1) 所提计及流-热耦合的热网络模型在不同负载电流下对IGBT模块的结温计算均具有较高的 精度。

(2) 所提计及流-热耦合的热网络法基于散热器冷却水温作为参考温度计算IGBT结温，在实际工程应用中更易于选取温度参考点，具有较好的工程应用前景。