叶表静压孔对平面叶栅性能的影响

张永超, 陆华伟, 孙震宇, 陈志龙

(1.中国航发上海商用航空发动机制造有限责任公司， 上海 201306； 2.大连海事大学船舶与海洋工程学院， 大连 116033)

平面叶栅试验过程中，为测量叶片表面静压，通常在叶片压力面和吸力面沿流向开设静压孔。为减少静压孔对流场干扰，提高静压测量精度，要求壁面静压孔设置在相对平直的位置，以降低气流离心力影响。然而，随着叶栅负荷提高，叶身曲率增大，在离心力与逆压共同作用下，静压孔会对流过叶表的气流产生干扰，造成测量误差。

已有的研究表明，叶表静压测量精度与开孔直径[1-2]以及来流马赫数相关，孔径越大，流线弯曲越严重，因而误差也就越大，而且随马赫数的增大而增大，但孔径太小不但制造加工困难，使用时容易被灰尘堵塞，而且会引起测量反应迟缓，延长试验时间[3]。此外，孔轴方向及孔的形状均会对静压测量结果产生影响，为降低开孔形状影响，孔口应光滑无毛刺，保持尖锐边，其轴线应与壁面垂直。同时为消除孔深的影响，一般要求开孔深度与孔径比值l/d≥3[3]，然而高压压气机中叶片尺寸小、厚度薄，在叶栅试验器尺寸一定情况下，为保证周期性，叶栅放大系数受到约束，因此该比值也难以绝对保证。

目前，对静压测量误差的研究不多，王宁等[2]开展了壁面静压小孔压力测量的雷诺数效应研究，获得了雷诺数与静压测量误差关系。随着新的叶型设计方法的应用[4]，叶型设计指标提高，载荷分布对叶型性能影响明显[5]，高马赫数、强湍流度、强逆压梯度等对静压测量精度的影响不应被忽略，测压孔的位置、形式的影响也不能简单采用以往经验进行评估。

1 问题导出

在某亚声速压气机叶栅试验过程中，为验证流场周期性，测量了中间四个叶片栅后尾迹，得到总压损失曲线随节距分布图，如图1所示，图中节距指相对值，为无量纲单位，比较发现，中间开设静压孔的两个叶片尾迹宽度与高度均大于相邻叶片。考虑到该试验叶片叶高只有100 mm，保证展弦比情况下弦长选取较小(约38 mm)，静压孔尺寸为φ0.6 mm，相对较大，推测静压孔破坏了原有型面轮廓，导致流动失真。为得到更接近实际的流动情况，对试验叶型进行放大，弦长增大至50 mm，并设置了不同尺寸的叶表静压孔，探究其对流场的影响程度与原因，为后续试验提供借鉴。

图1 栅后尾迹分布Fig.1 Distribution of wake

2 研究对象及数值方法

2.1 研究对象

研究对象为某亚声速压气机叶栅，该叶栅最大厚度<2.5 mm，如图2所示，具体几何参数及气动参数见表1所示。

β1为进口气流角，β2为出口气流角，βs为安装角，C为弦长，t为栅距图2 叶型示意图Fig.2 Sketch map of blade

叶片表面静压孔沿弦长14.4%～79.6%均布于吸力面侧，共20个静压孔，孔径分别为0.4、0.6、0.8、1.0 mm，分别以h0.4、h0.6、h0.8和h1.0表示，不带静压孔叶型以BL表示。

表1 叶型气动及几何参数

2.2 数值方法

建立平面叶栅计算模型，计算域进口取3倍弦长，出口取5倍弦长，采用Numeca划分结构化网格，如图3所示，前缘、尾缘及叶片表面网格进行加密，保证近壁面网格Y+<1。数值计算用ANSYS CFX求解器求解，为准确模拟近壁面流动状态，获取叶片表面附面层转捩特征，选择耦合γ-θ(间歇方程-雷诺数方程)转捩模型的剪切应力输运SST(shear stress transport)湍流模型，计算域进口边界条件设定来流总压、总温、入射角及湍流强度，出口设定静压值，叶片表面及上、下端壁设定无滑移绝热条件，节距方向设周期性边界条件。

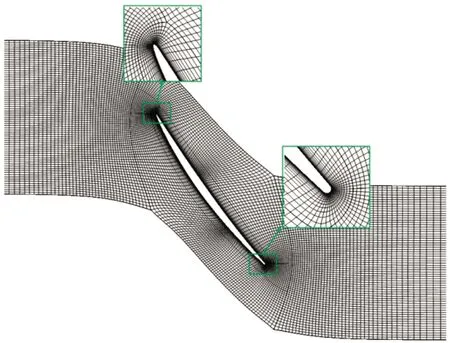
图3 网格示意图Fig.3 Sketch map of mesh

2.3 数值方法校核

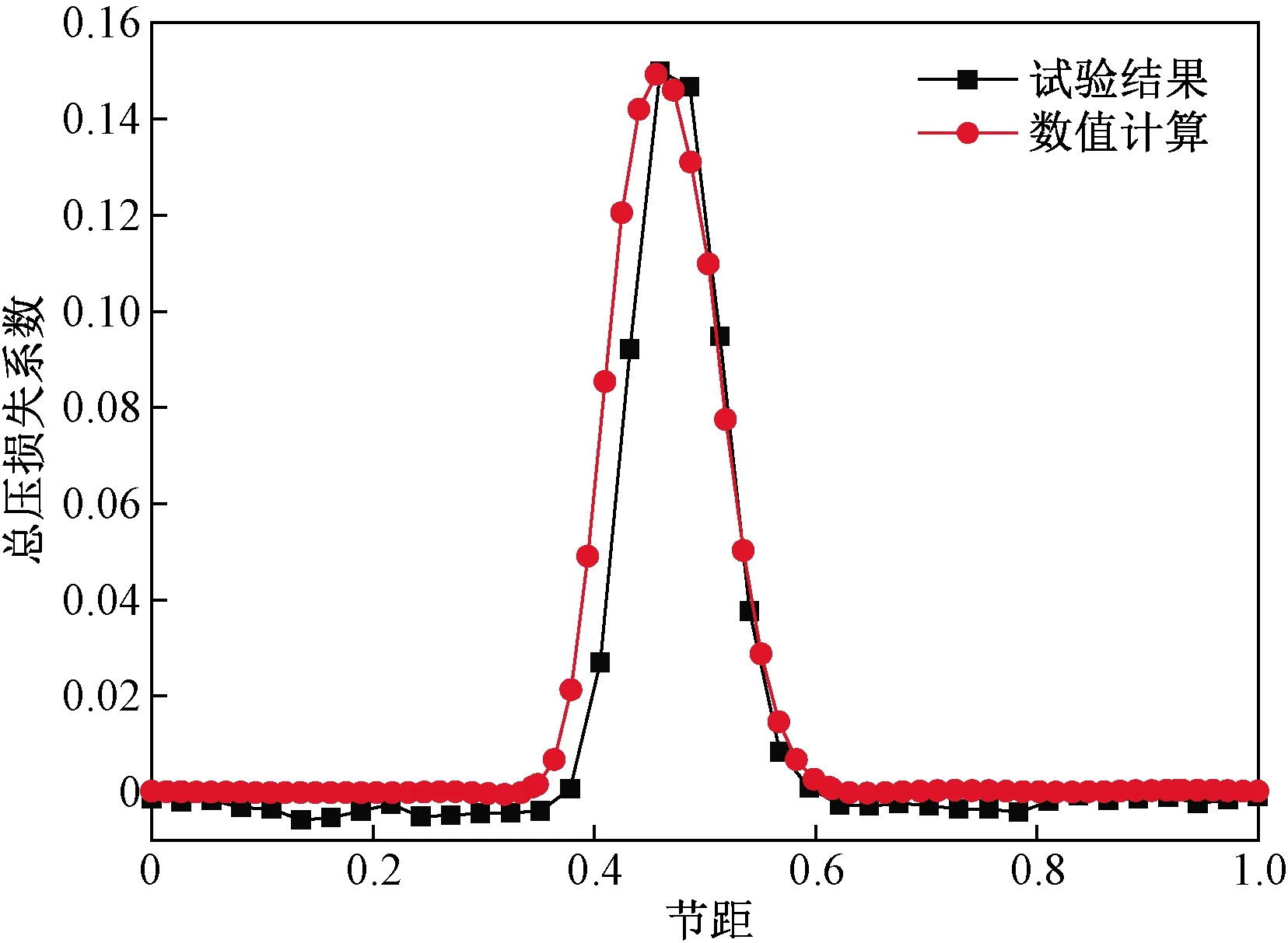
图4 数值校核Fig.4 Numerical verification

图4给出了无静压孔叶栅栅后总压损失的试验与计算结果，其中试验结果为展弦比2.6叶片栅后尾迹，数值结果为展弦比2.0叶片栅后尾迹，可以看出，计算与试验结果吻合较好，从而认证了数值计算结果的可靠性，同时说明了当前展弦比对叶栅性能影响较小。

3 结果分析与讨论

3.1 静压孔尺寸对叶表流场影响

叶片表面极限流线及静压分布可以表征近壁面流动特性，与附面层形态密切相关。如图5所示为计算所得叶片表面极限流线及静压分布结果，对于无壁面静压孔的叶栅(BL)而言，吸力面流动以角区分离及型面分离为主要特征，其中角区分离为端壁附面层“上洗”与吸力面附面层“下洗”形成集中脱落涡导致[6-8]。由型面分离线与再附线可知，在55%弦长位置处，吸力面附面层在强逆压作用下分离形成脱落涡面，随着逆压继续增大，该分离附面层在弦长80%位置处再附，脱落涡面回绕形成径向闭式分离泡[9]。

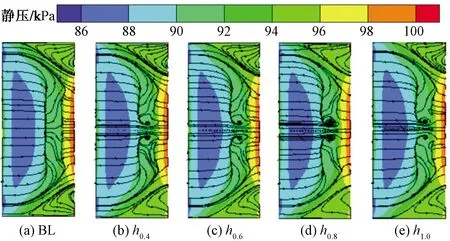
图5 叶片表面极限流线及静压Fig.5 Limit streamline and static pressure on blade surface

以来流总压和壁面静压计算得到叶栅50%叶高处等熵马赫数分布结果，如图6所示，压力面(pressure surface,PS)无静压孔影响，所有计算模型等熵马赫数分布完全重合，BL在吸力面(suction surface,SS)55%～80%弦长范围内存在马赫数平台，文献[10-11]指出，叶片表面马赫数平台的出现意味着流动分离的产生，附面层的分离点通常就是马赫数平台的开始位置，这与图5中叶型存在分离泡结果一致。静压孔对叶表等熵马赫数的影响表现为在55%～80%弦长范围内平台消失，取而代之的则是波浪形静压分布，而在80%弦长至尾缘段，叶栅表面等熵马赫数要高于BL，原因为叶栅中径处分离导致的堵塞效应消除，气流轴向速度得到提升。

提取各静压孔测量结果，得到图7所示的静压孔处等熵马赫数分布结果，0.4 mm静压孔测得的静压值略低于其他孔径结果，0.8 mm和1.0 mm静压孔测量结果中存在马赫数平台，但相比于BL结果，该平台向前缘方向移动，分布于55%～64%弦长位置，而0.4 mm和0.6 mm静压孔则未捕捉到这一细节，推断原因为相邻两个静压孔之间的附面层发生了分离与再附。

为量化表征各测压孔处静压偏离大小，定义静压相对偏差公式为

δ=(Ps-Ps,ref)/Ps,ref

(1)

式(1)中：Ps为静压孔处静压；Ps,ref为BL叶表静压值。

计算结果如图8所示，可知，自前缘至60%弦长位置处，静压孔处静压偏低，最大偏离度达到1%，在60%～75%弦长范围内，静压孔处静压偏高，偏离度在0.5%以上，最大达到2%，不同静压孔比较发现0.4 mm时偏差大于其他孔径结果。

图6 叶表等熵马赫数Fig.6 Isentropic Mach number of blade surface

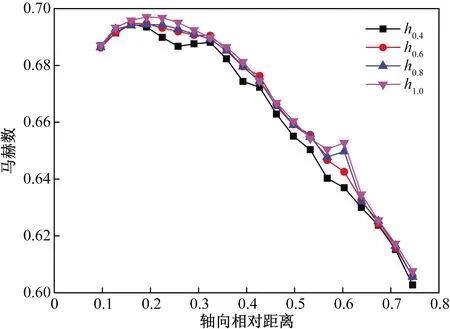
图7 静压孔等熵马赫数Fig.7 Isentropic Mach number of pressure holes

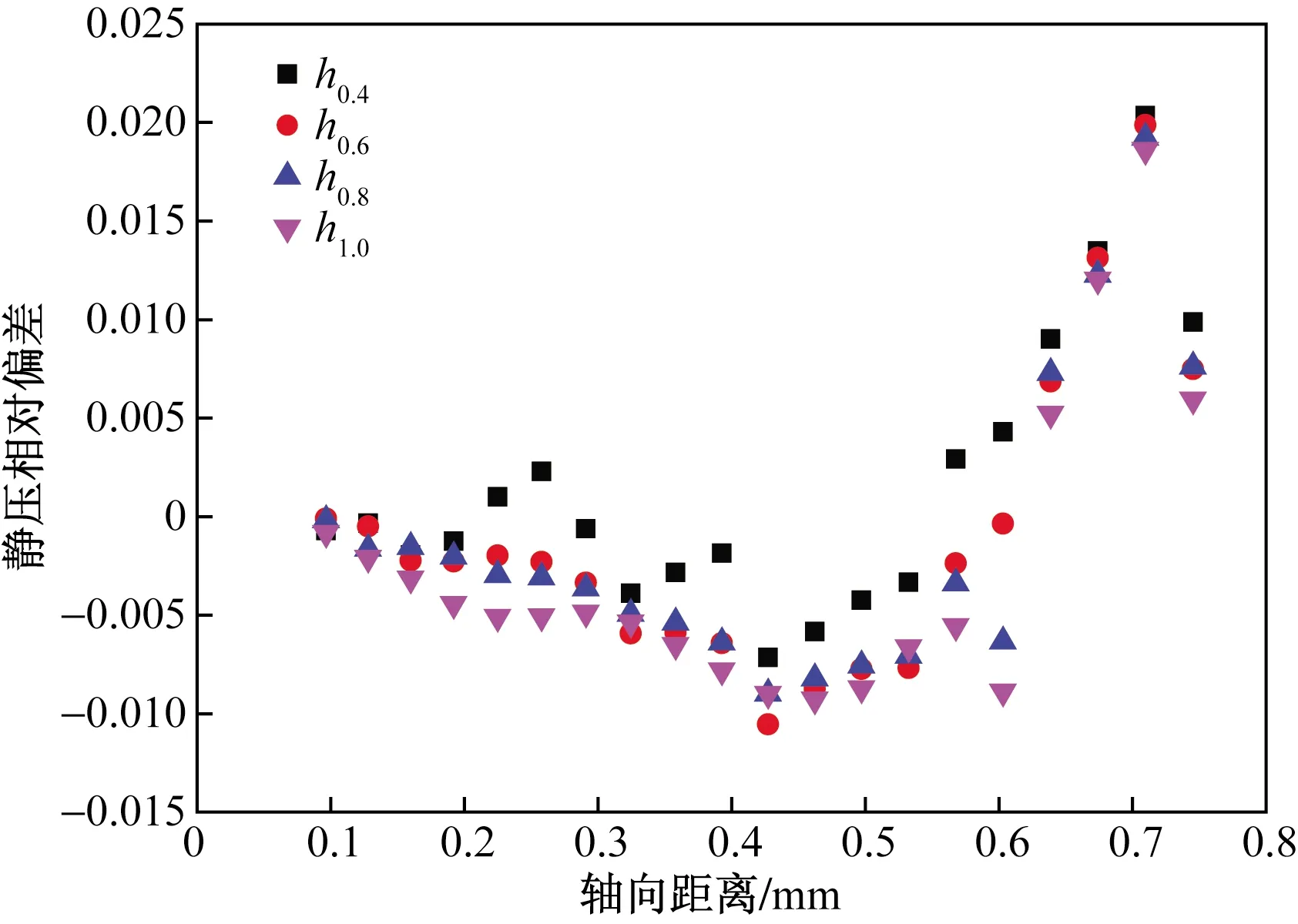
图8 静压相对偏差Fig.8 Static pressure relative deviation

3.2 静压孔尺寸对栅后流场影响

总压代表了气流做功能力，栅后总压损失是评估叶型的重要参数之一，通常以总压损失系数来表征，公式定义为

w=(Pt0-Pt)/(Pt0-Ps0)

(2)

式(2)中：Pt0为叶栅进口总压；Ps0为叶栅进口静压；Pt为出口当地总压。

图9所示为叶栅出口总压损失系数云图，由图9(a)可知，栅后总压损失以角区损失和型面损失为主，角区集中脱落涡向下游发展过程中，不断卷吸主流，气流掺混、扭旋、碰撞形成低能流体团[12-13]，中径处吸力面分离泡强烈的“位移效应”致使尾缘堆积大量低能流体，尾迹高损失区域较宽且损失峰值较大[14-15]。由壁面极限流线结果已知，静压孔的引入主要改变了叶栅中径处流场形态，对应于栅后损失，图9(b)～图9(e)，集中体现在型面损失的不同，表现为径向不连续，损失径向分布不均匀度增大，随着静压孔尺寸增大，中径位置处的损失核心随之增大。

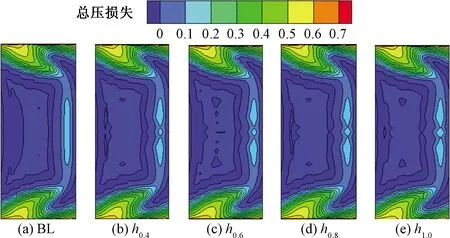
图9 栅后总压损失系数云图Fig.9 Counters of total pressure loss coefficient

为详细分析静压孔对栅后总压损失的影响程度，提取栅后50%和60%叶高处参数，得到其总压损失系数沿节距方向分布曲线，如图10所示，与BL结果相比，在50%叶高处，静压孔导致栅后尾迹宽度和高度不同，0.4 mm和0.6 mm静压孔下栅后尾迹中心向吸力面移动，宽度和峰值减小，0.8 mm和1.0 mm则正好相反，结果表明，静压孔影响了吸力面附面层，使得叶片吸力面的附面层厚度增大，由此造成的叶片出口的流动损失增大，口尾迹偏离叶片尾缘的中心位置，向吸力面方向偏离。在60%叶高位置处，不同尺寸静压孔对栅后尾迹影响规律一致，均表现为向尾迹中心远离吸力面，峰值增大。

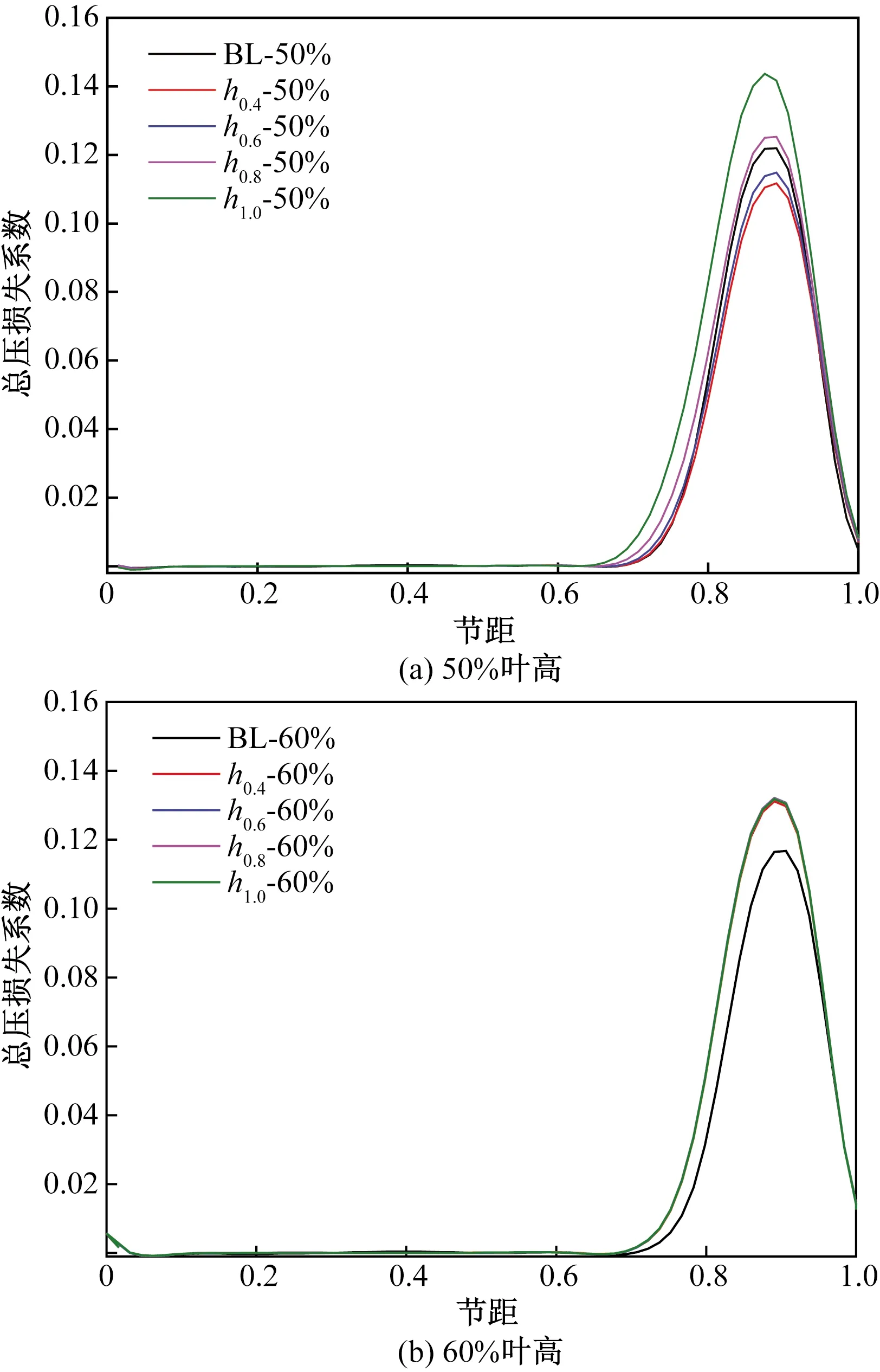
图10 栅后总压损失曲线Fig.10 Curve of total pressure loss coefficient

图11所示为栅后50%和60%叶高处气流角分布，与栅后尾迹变化类似，在50%叶高处，不同静压孔尺寸对气流角影响不同，表现为1.0 mm时偏大，其余孔径下偏小，而在60%叶高位置，静压孔导致气流角整体偏大。

为衡量总压损失系数和气流角变化量，定义相对总压损失系数Δw和相对气流角Δβ为

Δw=(w-wref)/wref

(3)

Δβ=(β-βref)/βref

(4)

式中：w为栅后总压损失系数节距平均值；wref为BL栅后总压损失系数节距平均值；β为栅后气流角节距平均值；βref为BL栅后气流角节距平均值。

图12所示为相对总压损失系数Δw和相对气流角Δβ随静压孔径变化情况，静压孔对总压损失系数的影响远远大于对气流角的影响，对于50%叶高，0.4 mm和0.6 mm静压孔分别使得栅后总压损失系数平均值降低6.5%和2.6%，气流角减小0.11%和0.12%，0.8 mm和1.0 mm静压孔则导致损失增大9.5%和30%，气流角分别减小0.05%和增大0.11%。在60%叶高处，0.4、0.6、0.8、1.0 mm孔径静压孔分别导致总压损失增大19.4%、20%、20.1%和19.9%，气流角增大0.17%、0.17%、0.17%和0.19%。

图11 栅后气流角曲线Fig.11 Curve of flow angle

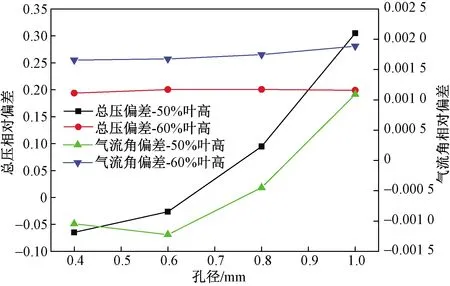
图12 相对总压损失系数和气流角Fig.12 Relative total pressure loss coefficient and flow angle

3.3 静压孔流场分析

图13所示为叶栅中径截面55%～80%弦长范围内叶片近壁面总压云图及速度分布，在BL中，可以见到清晰的涡核结构，即叶片表面闭式分离泡，涡致掺混导致该区域总压较低。叶片表面开设静压孔后，气流流经孔口时，流线会向孔内弯曲，并在孔内引起旋涡，该旋涡即是产生静压偏差的根源，此时静压孔扮演了类似旋涡发生器的角色，其内部旋涡的生成与脱落，产生了促进附面层分离泡转捩所需的扰动[16-17]，可达到抑制分离的目的，然而随着孔径增大，该旋涡强度随之增强，紧贴叶片表面的气流持续卷入、流出，导致气流沿程阻力增大，进而造成附面层厚度增加，因此叶片表面低能流体堆积，形成更大的型面损失。

壁面剪应力会对近壁面气流产生阻力，导致沿程附面层堆积，进而引发分离，图14所示为不同静压孔尺寸对应的壁面剪应力分布，在静压孔附近存在局部高剪应力区域，且随着静压孔尺寸增大，该区域减小，剪应力峰值降低，表明气体沿流向所受阻力逐渐增加，附面层厚度随之增长，叶片表面低能流体汇入尾迹，形成更大的尾迹损失。

图13 静压孔流线Fig.13 Streamline in pressure holes

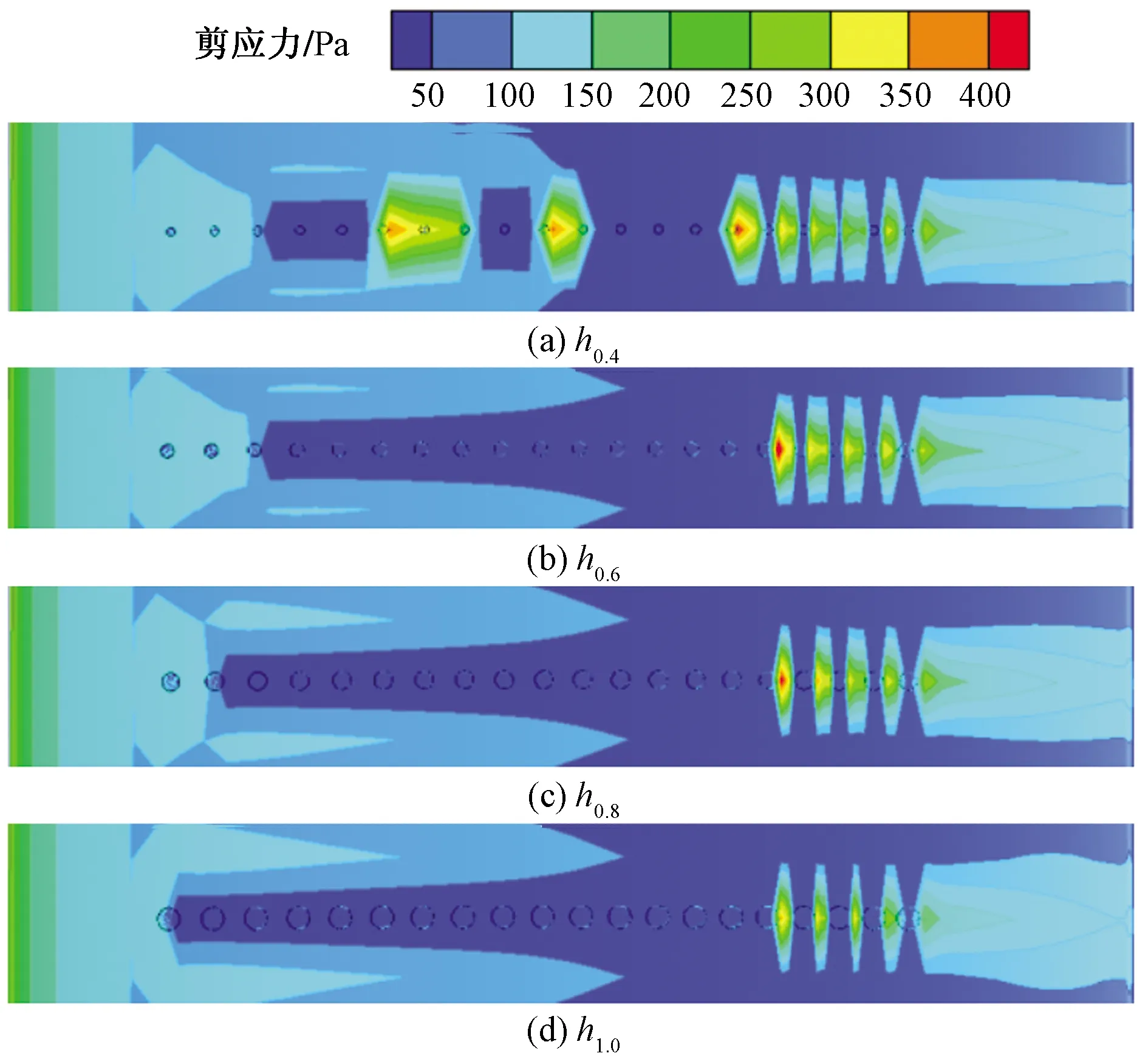
图14 壁面剪应力分布Fig.14 Wall shear on surface

4 结论

针对某试验用高压压气机叶栅，采用数值方法研究了不同尺寸静压孔对其性能影响，得出如下结论。

(1)叶栅中径处开设静压孔改变了原有叶栅型面流场形态，闭式分离泡被以螺旋结点为主要特征的径向涡所取代，分离泡造成的中径处等熵马赫数平台消失，静压分布呈现波浪形。

(2)与实际当地静压相比，静压孔测量结果偏离0.5%～2%，不同孔径比较，0.4 mm孔径造成的偏离最大。

(3)静压孔对栅后损失的影响远大于对气流角的影响，栅后尾迹中心发生偏离，在50%叶高处，0.4、0.6 mm静压孔导致栅后总压损失系数平均值降低6.5%和2.6%，0.8 mm和1.0 mm则导致损失增大9.5%和30%，在60%叶高位置处，所有静压孔均导致损失增大，最大20.1%。

(4)对静压孔内流场分析得知，静压孔内旋涡是产生静压偏差的根源，随着孔径增大，旋涡强度增大，有旋气流的生成与脱落对流体产生扰动，进而造成附面层厚度增加，叶片表面低能流体堆积，形成更大的型面损失。