基于模糊故障树的建筑施工高处坠落全面风险评估

安慧, 黄艾, 安敏, 范历娟, 金镁

(1.三峡大学水利与环境学院， 宜昌 443002； 2.三峡大学水库移民研究中心， 宜昌 443002； 3.三峡大学经济与管理学院， 宜昌 443002； 4.葛洲坝集团交通投资有限公司， 武汉 430000)

建筑行业面临许多职业伤害和死亡风险，因其户外作业和高空作业的特点，高处坠落是具有高发性和高危害性的建筑事故[1]。发生高处坠落事故不仅对企业的经济、声誉、发展产生巨大影响；同时对人员的生命安全产生威胁，给家庭带来重大打击；甚至会影响社会稳定[2-3]。相比于传统建筑，超高层建筑是一个更为复杂的系统，其高度更高、规模更大、结构形式更多样、功能更繁多、建设标准更高。对于这样一个复杂系统，其事故原因涉及人、机、料、法、环、测等多重要素，每个要素在现场又是复杂多变、环环相扣的，从建筑设计、施工过程、材料、设备到人员工作，任何一个要素出现问题都可能引发安全事故[4]。因此，深入分析高处坠落事故产生的原因，开展建筑施工高处坠落风险评估及风险后果分析，通过采取安全管理措施可减少伤亡事故发生，提高高处作业的可靠性。

目前，学者们对于高处坠落事故的风险评估分为定性分析和定量分析，在定性分析方面，众多学者通过事故分析法、文献挖掘法、因果分析法或采用故障树分析法等深度分析了事故原因。如李钰等[5]利用文献挖掘法，以事故调查报告为基础，构建了高处坠落事故的致因集合，并明确出28项事故致因因素。张淑玲等[6]通过因果分析方法，从人、物、方法、环境和管理方面分析了建筑施工高处坠落事故的原因。刘朝阳等[7]以事故树为架构，针对桥梁工程从定性角度分析了高处坠落事故发生的影响因素。以上学者都从定性的角度分析了高处坠落事故的致因因素，但仅从定性的角度无法估量风险大小，于是有学者从定量的角度对高处坠落事故风险进行了分析。采用的主要分析方法有“2-4”模型、解释结构模型、故障树分析法等。孙世梅等[8]采用行为安全“2-4”模型从行为原因方面研究了事故的发生规律。郑霞忠等[9]通过建立高处坠落事故人因失误结构方程模型研究人因事故的产生机理，识别了关键人为失误因素和关键路径。李永清等[10]、张玉明等[11]通过构建建筑施工高处坠落解释结构模型分析了各影响因素间的相互关系，并根据分析得出的影响因素的作用路径提出相应对策。高姝蕾[12]利用故障树分析法确定了高处坠落事故底事件的结构重要性，同时计算了关键因素重要度和发生概率。Shi等[13]基于“人-机-环境-管理”的复杂系统，建立了高空坠落危险性评价的层次模糊评价模型，给出了风险评估。

可以看出，学者们针对高处坠落事故进行了大量研究，但是以上研究没有将定性分析与定量计算有效结合起来；且在构建事故致因评估模型时，多以专家主观判断为基础，但事故致因因素存在模糊性与不确定性，专家的经历与经验也不尽相同，使得判断结果具有一定的误差，从而导致分析结果缺乏客观性与准确性；另外，现有研究大多只识别出关键致因要素，但并未针对这些关键致因要素进行风险后果分析，评估结果无法全面表征出实际风险大小，使得管理人员因仅对风险存在片面的认识而忽略了对风险的防范与控制。为解决以上问题，现拟将模糊集理论与故障树分析法相结合，对超高层建筑施工高处坠落事故成因进行分析，寻找主要的风险因素，进而运用建筑施工高处坠落风险矩阵来评估风险后果，评定风险等级，从而更精确地表征风险大小。以期为管理人员制定高处坠落预防措施并对现场管理提供更具针对性建议，有效防范此类事故的发生。

1 高处坠落模糊故障树风险分析模型

1.1 基于模糊集理论的故障树分析流程

使用模糊故障树模型对建筑施工高处坠落事故发生可能性评价的流程如图1所示。

图1 风险评估流程Fig.1 Risk assessment process

1.2 故障树分析法

故障树分析(flaut tree analysis,FTA)法是一种逻辑演绎推理方法，其思想是选取系统中需要分析的事件作为顶事件，通过因果关系逐层分析找出引起顶事件发生的直接原因作为中间事件，继续分解到无法进行分解的故障原因作为底事件，各层事件之间通过逻辑门连接[14-15]，即得到一个故障树。故障树分析法具有直观、因果关系清晰、逻辑性强的特点，是安全系统工程中被用来分析重大安全事故因果关系的重要方法之一[16-17]。传统的故障树分析需要精确的底事件概率才能有效计算出顶事件失效概率，但是，对于施工项目来说，很难获得各底事件的精确概率，其主要原因：一是项目建设周期长，外界环境易发生重大变化导致项目建设发生突发情况，无法准确进行预测；二是项目建设具有一次性和独特性，历史事故的统计数据不能完全用于评估当前项目事故的发生率，且由于时间和成本的限制往往无法统计大量的历史事故获得可靠性数据；三是由于造成事故发生的各种因素相互交错，定义界限不明确，且人为判断有误差和不一致性，使得大量事件存在模糊不确定性。这种情况下，纯概率法得出的结果并不精确。然而，引入模糊综合评判法可有效解决以上问题。模糊故障树分析法既可进行定性分析[18]，通过因果结构关系找出所有能使故障事件发生的底事件组合，并依据结构重要度排序确定各致因因素对故障事件产生影响的大小，为管理人员确定采取防范与整改措施的优先顺序提供基本的依据；又可进行定量分析和系统评价[19]，识别出关键致因因素，为制定有针对性的管理措施提供定量分析依据。其分析结果对于管理人员来说相当于一个形象的管理维修指南，有助于他们及时发现问题，进行有针对性的防范与整改，可提高建筑施工高处坠落系统的安全性和可靠性。因此，应用模糊故障树分析法可以简单有效地对建筑施工高处坠落事故进行风险评估。

故障树定性分析包括最小割集与结构重要度，两者关系式为

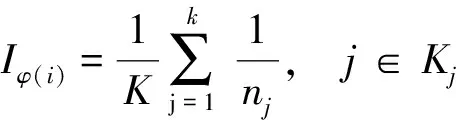
(1)

式(1)中：Iφ(i)表示第i个底事件的结构重要度；K表示最小割集总数；Kj表示第j个最小割集；nj表示第i个底事件所在的第Kj最小割集中的底事件总数。

故障树定量分析包括概率重要度系数[IP(Xi)]和临界重要度系数[C(Xi)]，计算公式分别为

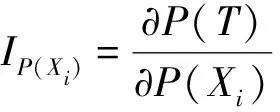
(2)

(3)

式中：P(T)为顶事件T的概率；P(Xi)为底事件Xi发生的概率。

1.3 基于模糊理论和专家评判法的模糊概率求解

传统的故障树分析需要精确的底事件概率才能有效计算出顶事件失效概率，但是由于工程项目的特殊性，大多底事件是不确定且模糊的，无法有效获得其失效概率。因此，通过经验丰富的专家对底事件进行人为判断是一种行之有效的方法。另外，模糊集理论[20]可以平衡事故致因因素的模糊性与不确定性[21]。因此，可利用模糊集理论并结合专家综合评判的方法来量化高处坠落事故的失效概率。

有研究显示专家在综合评判2个元素时，评判标准划分在5～9具有更高的准确性和有效性[22-23]。因此，邀请专家采用5种语言值对建筑施工高处坠落事故的底事件进行评估，评估语言包括：小(L)、较小(RL)、中等 (M)、较大(RH)、大(H)，分别表示事故致因因素对故障事件的影响程度。当使用自然语言进行不确定描述时，需要采用模糊隶属函数[24]将其定量表述出来。因为梯形模糊函数具有距离较为宽广的属性，计算过程简单、高效，因此采用梯形模糊隶属函数(图2)来映射专家评判语言。表达式为

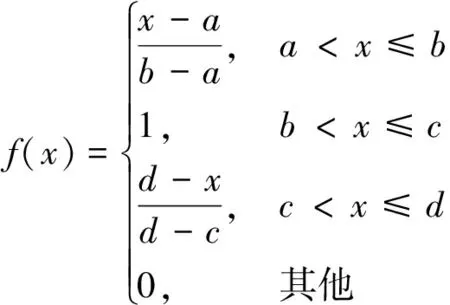
(4)

式(4)中:a和d分别表示梯形模糊数的上下界；区间[b，c]表示梯形模糊数的中值。

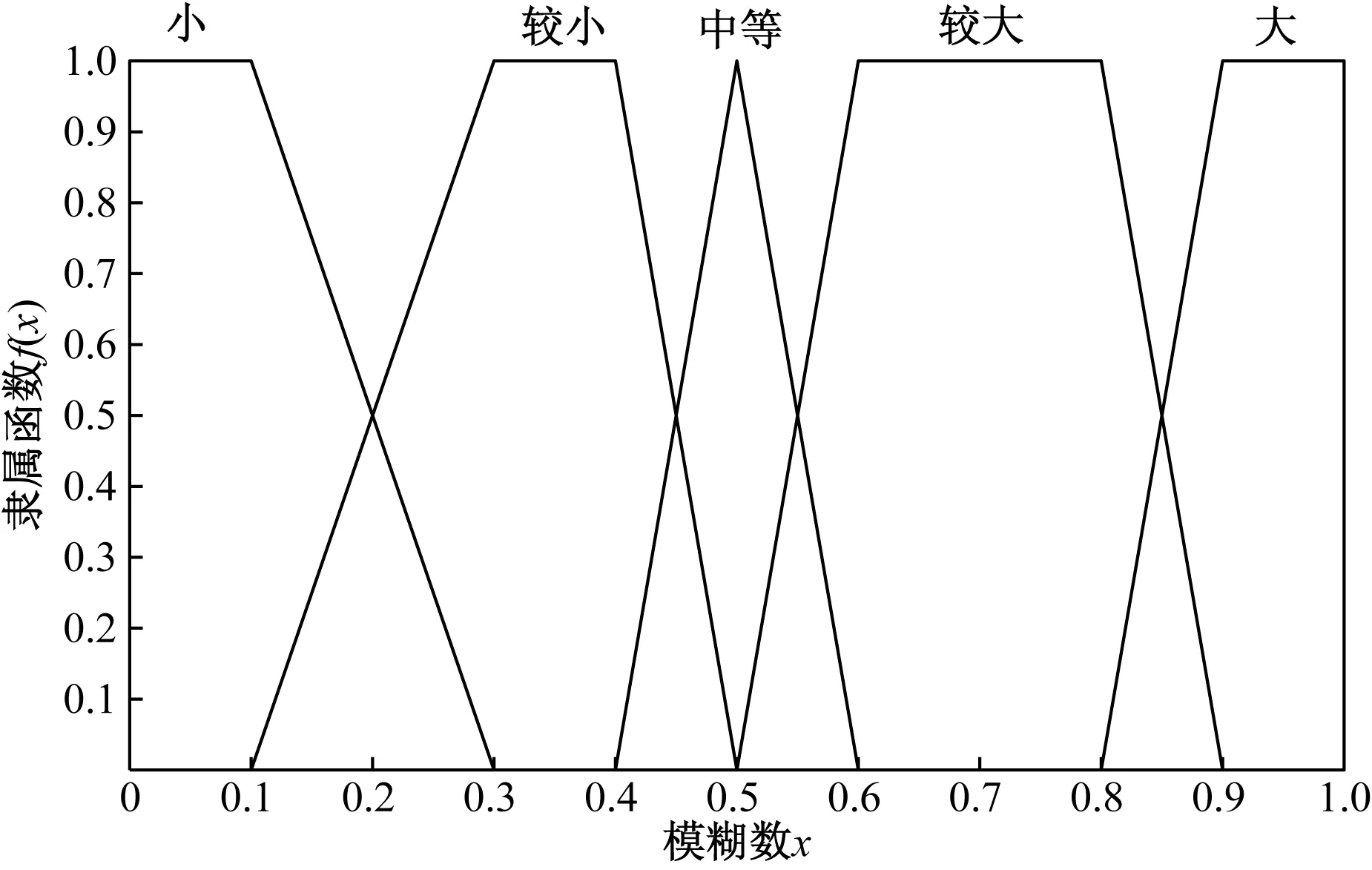
图2 专家判断的自然语言模糊数Fig.2 Natural language fuzzy numbers of expert judgment

不同的专家对同一事物的看法往往与其经历和经验相关，也就可能出现专家的判断存在冲突和一致的情况，但由于造成高处坠落事故发生的事件本身具有模糊、难以量化的特点，也就无法明确专家判断的正确与否。 Hus和Chen提出的算法[25]是一种将个体模糊意见聚合成一组模糊一致意见的方法，可消除以上专家判断出现矛盾的情况，降低主观性。因此，将采取该算法对专家意见进行聚合处理，步骤如下：

(1)确定相似度。

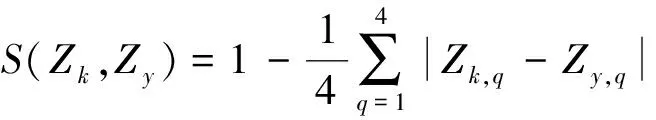
(5)

式(5)中：Zk、Zy分别为第k、y位专家的评估语言；q为模糊数；S(Zk，Zy)为两个专家评估语言的相似度，0≤S(Zk，Zy)≤1。

(2)确定平均一致程度。

(6)

式(6)中：N为专家总数。

(3)确定相对一致程度。

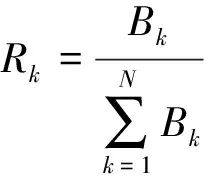
(7)

(4)确定聚合权重。因各专家的经历和经验不同，所作评估的权威性也不同，需对各专家分配不同的权重值。通过职称、学历和工龄三方面对专家进行不同的赋值[26-27]，给出不同专家的权重值φk，具体赋值情况如表1所示。则聚合权重为

Wk=βφk+(1-β)Rk

(8)

式(8)中：β为松弛因子，反映看重个体意见还是群体意见，β∈[0,1]。

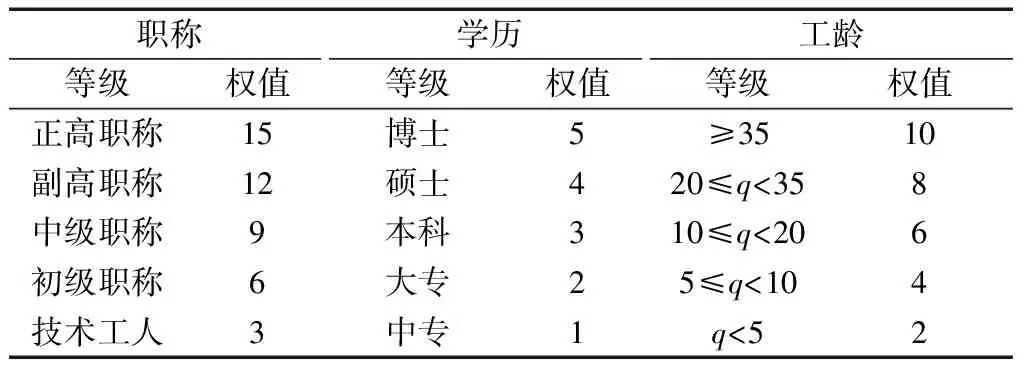
表1 专家能力指标体系

(5)汇总不同的专家意见，确定底事件的模糊数。为便于模糊数的合成运算，应用模糊集合中的α截集理论将模糊数转化为区间数再进行计算，梯形模糊数Fα的α截集区间数计算公式为

Fα=[a+(b-a)α,d-(d-c)α]

(9)

模糊数形式和α截集见表2。

表2 模糊数形式和α截集

则应用α截集下专家组评价的平均模糊数为

(10)

(6)计算模糊可能性值。专家给出的评判语言量化后仍是模糊数，具有不确定性，采用左右模糊排序法[28]将其转化为模糊可能性值FPS[29]，首先需要获得模糊最大化集和最小化集，分别为

(11)

(12)

则左右模糊可能度分别为

(13)

(14)

模糊可能性值为

(15)

(7)计算模糊失效概率。最终计算的模糊失效概率是一个精确地概率值，本文中通过Onisawa公式[30]进行计算，即

(16)

(17)

2 风险后果分析模型

建筑施工高处坠落事故会造成多种风险后果，选取发生事故后直接影响最大且具有普遍性的风险后果进行分析，即从人员伤亡、经济损失和社会影响3方面来评估[2]。城镇化建设的工作原则是以人为本、安全第一，因此将人员伤亡放在第一位；其次安全事故的发生会让一个家庭直接失去经济来源，会给企业造成重大利益损失，与民生息息相关，因此将经济损失放在第二位；相比于人身安全和民生问题，发生安全事故造成的社会影响可放在第三位，将其权重分别设为0.5、0.3、0.2[31]。根据生产安全事故等级的分类标准建立建筑施工高处坠落的风险后果分级标准[32]，如表3所示。风险后果的综合评价值计算公式为

Ri=0.5d1i+0.3d2i+0.2d3i

(18)

式(18)中：dij为人员伤亡、经济损失和社会影响的风险评估。

依据梯形模糊数的运算法则求出各底事件的风险概率，建立建筑施工高处坠落各个风险因素的概率定量分级标准，如表4所示。

然后，构建5×5的风险矩阵[32]，如表5所示。其中，假定Ⅰ为低风险记2分，Ⅱ为一般风险记4分，Ⅲ为中等风险记6分，Ⅳ为较高风险记8分，Ⅴ为高风险记10分。

表3 风险后果分级标准

表4 风险概率分级表

表5 模糊风险矩阵

图3 建筑施工高处坠落故障树Fig.3 Fault tree of falling accidents of building construction

最后，将所有得分相加得到建筑施工高处坠落的风险总值C[31]，即

(19)

式中：m为风险事件的总数;Ri为各风险事件的风险后果得分。

将建筑施工高处坠落风险评价值占风险总评价值的比例记为Q=C/(10m)，并按照如表6所示的标准对建筑施工高处坠落风险等级进行划分。

表6 模糊风险分级

3 实例分析

以上模型可以量化高处坠落的风险，下面通过实例进行验证。宜昌市某地区在建超高层建筑主楼高230 m，是一栋45层的综合体，是目前宜昌在建最高楼。此建筑一旦发生高处坠落事故，将会产生严重的风险后果，对生命安全和经济财务的危害性极大，需进行风险评估并采取相应的措施来避免事故发生。针对该案例实况并咨询参与该项目的业内专家意见对可能造成建筑施工高处坠落事故的风险因子进行识别，最终确定的风险因子如表7所示。然后在风险识别的基础上构建该工程建筑施工高处坠落的故障树，如图3所示。假设建筑施工高处坠落的底事件是相互独立且仅有发生与不发生两种状态。然后根据已建立故障树引入模糊集理论对该案例高处坠落风险事故作如下分析。

3.1 定性分析

3.1.1 求最小割集

通过布尔代数分配法求解，得到该案例共有630组最小割集：K1={X1,X11,X20}，K2={X1,X11,X21}，…，K630={X10,X19,X26}。说明建筑施工高处坠落事故发生的潜在组合共有630个，数量较大，体现了施工现场的危险源较多，易发生事故，应采取一定的措施进行预防。

3.1.2 结构重要度分析

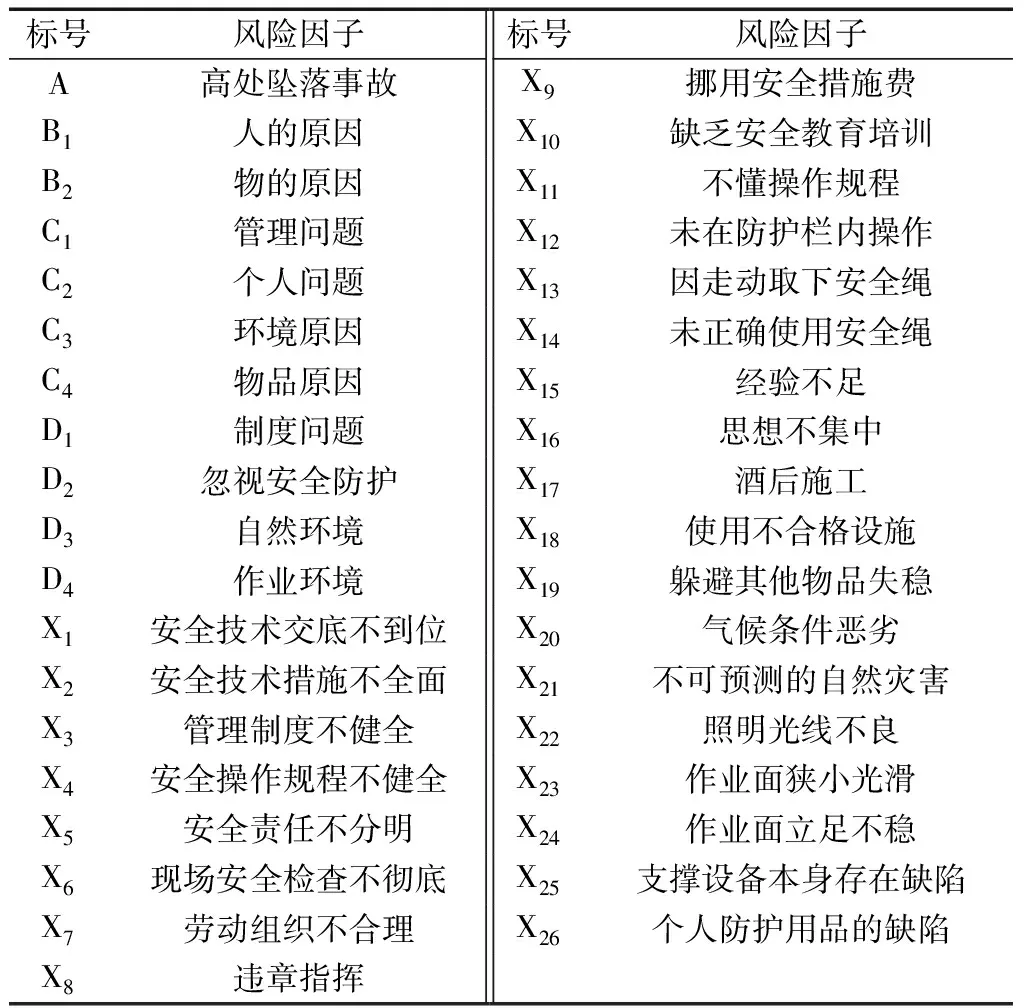
表7 建筑施工高处坠落事故风险因子

Iφ(12)=Iφ(13)=Iφ(14)=Iφ(15)=Iφ(16)=Iφ(17)=Iφ(18)=Iφ(19)>Iφ(1)=Iφ(2)=Iφ(3)=Iφ(4)=Iφ(5)=Iφ(6)=Iφ(7)=Iφ(8)=Iφ(9)=Iφ(10)。

由以上排序可看出底事件X20～X26对建筑施工高处坠落事故的发生影响最大，其次是X11～X19，集中在个人因素和环境因素。为了降低建筑施工高处坠落风险，更要针对以上因素提出防治对策。

3.2 模糊概率求解

首先计算出各底事件的失效概率，以安全技术交底不到位X1为例进行介绍。通过电子邮件发送调查问卷向三位涉及该项目建设的行业专家[一位资深专家(职称：正高，学历：博士，工龄：≥35)、一位教授(职称：副高，学历：博士，工龄：20≤q<35)、一位资深建筑事故调查官(职称：副高，学历：本科，工龄：20≤q<35)]获取评估语言，三位专家对该事件的评估语言分别为较小、大、较大，利用式(5)～式(8)可以求出三位专家意见的平均一致程度B1=0.562 5，B2=0.637 5，B3=0.700 0，相对一致程度R1=0.296 1，R2=0.335 5，R3=0.368 4；三位专家的能力权重φ1=0.384 6，φ2=0.320 5，φ3=0.294 9，对评估意见进行聚合，式中α取0.5，则W1=0.340 3，W2=0.328 0，W3=0.331 7。然后，根据式(9)～式(15)得出左右可能性值为FPS,R(W)=0.739 2，FPS,L(W)=0.498 3 ，FPS,T(W)=0.620 5。最后，利用式(16)、式(17)去模糊化，求得模糊数FFR=0.011 1，即发生安全技术交底不到位的概率为0.011 1。

依次类推可计算出其他模糊事件的失效概率，如表8所示。

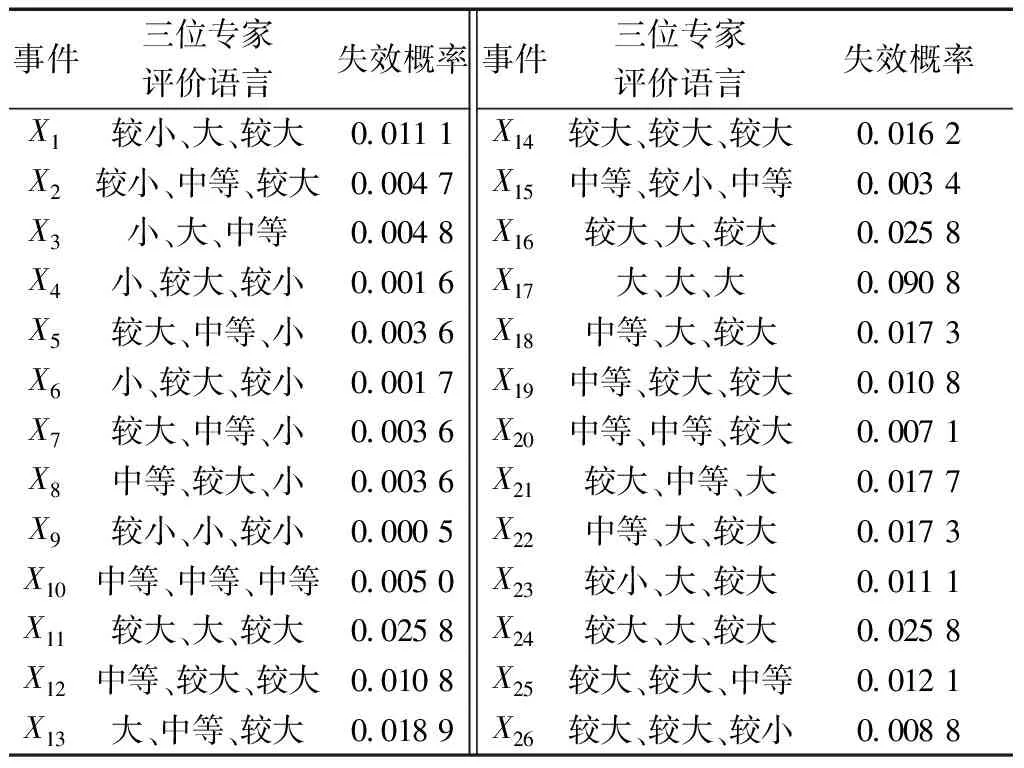
表8 底事件失效概率

3.3 定量分析

首先计算出每个最小割集发生的概率：P(K1)=2.036×10-6，P(K2)=5.074×10-6，…，P(K630)=6.57×10-7。进而求得该建筑施工高处坠落事故的失效概率为P(T)=P(K1)+P(K2)+…+P(K630)≈8.849×10-4。

根据式(2)、式(3)分别计算出各底事件的概率重要度系数IP(Xi)和临界重要度系数C(Xi)，如表9所示。

表9 底事件重要度系数

临界重要度系数反映了底事件的重要程度，它是制定建筑施工高处坠落防范措施的一个重要依据。通过以上计算可以看出，结构重要度相同的不同底事件对顶事件发生的敏感程度也不一样，尽管事件X1和事件X23的发生概率相同[P(X1)=P(X2)=0.011 1],但是X1在系统中比X23重要[IP(X1)>IP(X23)],而虽然事件X17和事件X18在敏感度系统中对顶事件的影响相同[IP(X17)=IP(X18)=0.004 0]，但是X17要比X18更容易导致顶事件的发生[C(X17)>C(X18)]，因此X17要比X18优先解决。结合临界重要度系数与概率重要度系数可更加精确识别出风险因子的重要程度，其中，临界重要度系数大于0.1的共有12项风险因子，排除其中两项概率重要度系数为0.004的风险因子，确定出X1、X2、X3、X10、X17、X21、X22、X23、X24、X25为主要导致高处坠落事故的底事件，需要优先解决。

通过建筑施工高处坠落风险定性与定量分析可以了解到：高处坠落事故的发生并不是单一因素造成的，往往是多个因素共同作用的结果，单个风险因子在整个系统中的重要度不是取决于它本身的概率大小，而是在于它所在的最小割集在整个体系中所处的位置，对于处于同一地位的风险因子，则可以通过临界重要度系数划分优先级。尽管风险因子发生的概率差不多，它们在系统中的作用类似，依然可以划分出哪些风险因子属于应尽早修改的，哪些风险因子可以放缓一段时间，而且可以很清晰地了解到各风险因子之间的逻辑关系。通过该案例识别出的缺乏安全教育培训、安全技术交底不到位、支撑设备本身存在缺陷、恶劣的自然环境等事故致因要素为管控重点，要优先进行排查与防范。

3.4 风险后果分析

针对以上主要导致高处坠落事故发生的底事件计算其风险后果，结合表3可知X1、X2、X3、X10、X17、X21、X22、X23、X24、X25的风险概率等级。再请以上3位专家对这10个风险事件可能导致的风险后果进行评分，根据式(18)处理得到风险等级，如表10所示。

表10 风险分级表

将以上各风险事件的得分进行汇总，由式(19)得到建筑施工高处坠落风险分值C=79.7，进而得到建筑施工高处坠落风险评价值占风险总评价值得比为Q=0.797。对照表6模糊风险分级表得出建筑施工高处坠落风险后果等级为四级，属于较高风险。

针对事故致因要素进行风险后果分析，更准确地表征了实际施工过程中的风险大小，尽管该案例发生高处坠落事故的概率较小，但是引起的后果很严重，提示管理人员不可松懈对施工安全的管理，在实际操作过程中要多加防范。

4 结论

运用故障树分析法、模糊数学理论和风险矩阵建立建筑施工高处坠落系统可靠性分析模型，并利用工程实例对所建评估模型的可行性进行验证，得到如下结论。

(1)将故障树分析法和模糊集理论结合运用到建筑施工高处坠落事故成因及风险分析中，从定性和定量的角度评估高处坠落事故致因要素及失效概率。该方法克服了传统分析法中难以获得底事件精确概率以及专家评判法存在误差的问题，使得评估结果更加准确。

(2)针对定性与定量分析确定的建筑施工高处坠落事故致因要素运用风险矩阵来评估风险后果，更准确地表征了实际施工过程中的风险大小，有助于管理者及时根据评估结果加强监管。

(3)通过案例实证方法的可用性和有效性。研究发现该案例发生高处坠落事故的概率较低，风险后果评估等级为较高风险，缺乏安全教育培训、安全技术交底不到位、支撑设备本身存在缺陷、恶劣的自然环境等事故致因要素为管控重点。因此，管理人员需要高度重视，加强现场监管。同时表明，模糊故障树分析法结合了概率不精确性和工程不精确性，使复杂的问题变得简化，提高了灵活性，在可靠性工程中有很大的应用价值。