基于行为经济学前景理论的出行决策

汤静妍, 胡明伟，2，3，4*, 何国庆

(1.深圳大学土木与交通工程学院， 深圳 518060； 2.深圳大学滨海城市韧性基础设施教育部重点实验室， 深圳 518060； 3.深圳大学未来地下城市研究院， 深圳 518060; 4.深圳市地铁地下车站绿色高效智能建造重点实验室， 深圳 518060)

随着中国汽车保有量的增加，交通拥堵问题日益严重。居民出行方式选择是交通拥挤问题重要的原因之一，私人交通方便、舒适，但道路使用率低，且费用较高，而公共交通运量大、占用道路资源少，提高公共交通的分担率能有效缓解这一难题。张介诚[1]探讨了在不同影响因素下的私家车与公共交通出行的选择函数，并通过卡方检验分析出行时间与出行方式的内在联系。

行为经济学将心理学与经济学有效结合，通过分析个体或群体的心理研究其经济行为特征。行为经济学中前景理论(prospect theory)适用于有限理性出行者的决策行为。前景理论的一大改进就是用价值函数替代了传统的期望效用理论(expected utility theory)中的效用函数，克服了期望效用理论认为决策者是完全理性的不足。提高其解释力的同时拓宽了应用范围，得到国内外学者的广泛推崇。Chirag等[2]利用前景理论将新闻销售商处于损失框架时会以一种寻求风险的方式行事的现象。Chang等[3]通过前景理论研究金融市场上不确定的投资问题，发现不同投资者对风险的不同态度。Ghader等[4]利用前景理论研究出行方式的选择如何受到出行时间可靠性的影响。姚兰[5]运用累积前景理论研究了出行者在不确定环境下对出行方式的选择。郭鸿钧等[6]提出一种基于前景理论和灰色关联方法的运输通道出行决策方法，分析不同定价策略和速度对运输通道分担率造成的影响。

在计算各种出行方式的前景值时，很多研究将其本身的期望成本看作参照点，因此采用同一个期望成本进行计算。陈磊等[7]从外部竞争优势与内部自身特点两个方面提出了参照点的设置方法，构建了反映决策者偏好的交叉效率模型。徐君翔等[8]选取运输时间和路段动态风险度为参照点，构建基于双参照点的应急物流路径选择模型，研究了运输者决策行为和风险度差异对应急物流路径的选择影响。但在实际出行中，出行者往往是衡量其出行成本对比其他交通方式的期望出行成本是收获还是损失进行决策的。因此，本文以其他交通方式的期望成本作为参照点来计算该交通方式的前景。

交通政策可以通过经济调控手段影响出行者的出行选择，缓解交通压力。目前在运用前景理论对出行方式选择的研究中，主要集中在出行者主观属性、交通方式客观特性等微观影响因素，较少从宏观层面考虑交通政策对出行者决策行为的影响。国外已有新加坡、伦敦等国家和城市实施拥堵收费政策，Anas[9]描述了洛杉矶拥堵定价为交通和经济带来的可观收益。中国有学者对此进行探讨，但尚未在实际生活中应用。胡严艺等[10]通过引入Logit模型理论，构建不同碳排放收费率下居民出行模式的选择。王敏等[11]通过对简化的MNL模型进行数学仿真，分析拥堵收费对居民出行方式的影响。贾书伟等[12]利用系统动力学与灰色系统相结合的方法(system dynamics-grey model, SD-GM)，构建了交通拥堵收费模型，并通过仿真实验，分析环境出行的可行策略。总的来说，过去的研究所选取的参照点较为单一，且未区分政策前后对居民出行决策的影响，同时缺乏对不同政策情境下改进出行决策的相关研究。

基于以上研究，现根据服务对象的区别，将公交车、地铁、私家车、出租车四种交通方式，划分为公共交通(public transportation)和私人交通(private transportation)两类，且以其他交通方式的期望成本作为参照点用以计算前景值。同时根据两种政策，建立拥堵收费和票价折扣的混合策略。通过算例研究不同标准下的拥堵收费和票价折扣对出行者决策行为的影响。为缓解交通拥挤问题及相关部门设置合理的城市交通需求管理政策标准提供参考，稳定既有公共交通出行人群的同时吸引更多私人交通出行者也转向公共交通。

1 基于前景理论的出行决策建模步骤

基于前景理论将出行决策建模步骤(图1)分为编辑阶段和评价阶段。编辑阶段是对各出行方案进行基本的分析，为评价阶段奠定基础。首先出行者需要主观感知各交通方式的出行成本，根据设置的参照点来衡量所选交通方式的决策结果是“收益”还是“损失”，再确定价值函数和权重函数的参数设置。评价阶段是在编辑阶段的基础上，通过价值函数和概率权重函数计算各出行方案的前景值并做出评价的过程，选择前景值最大的交通方式作为出行决策结果。

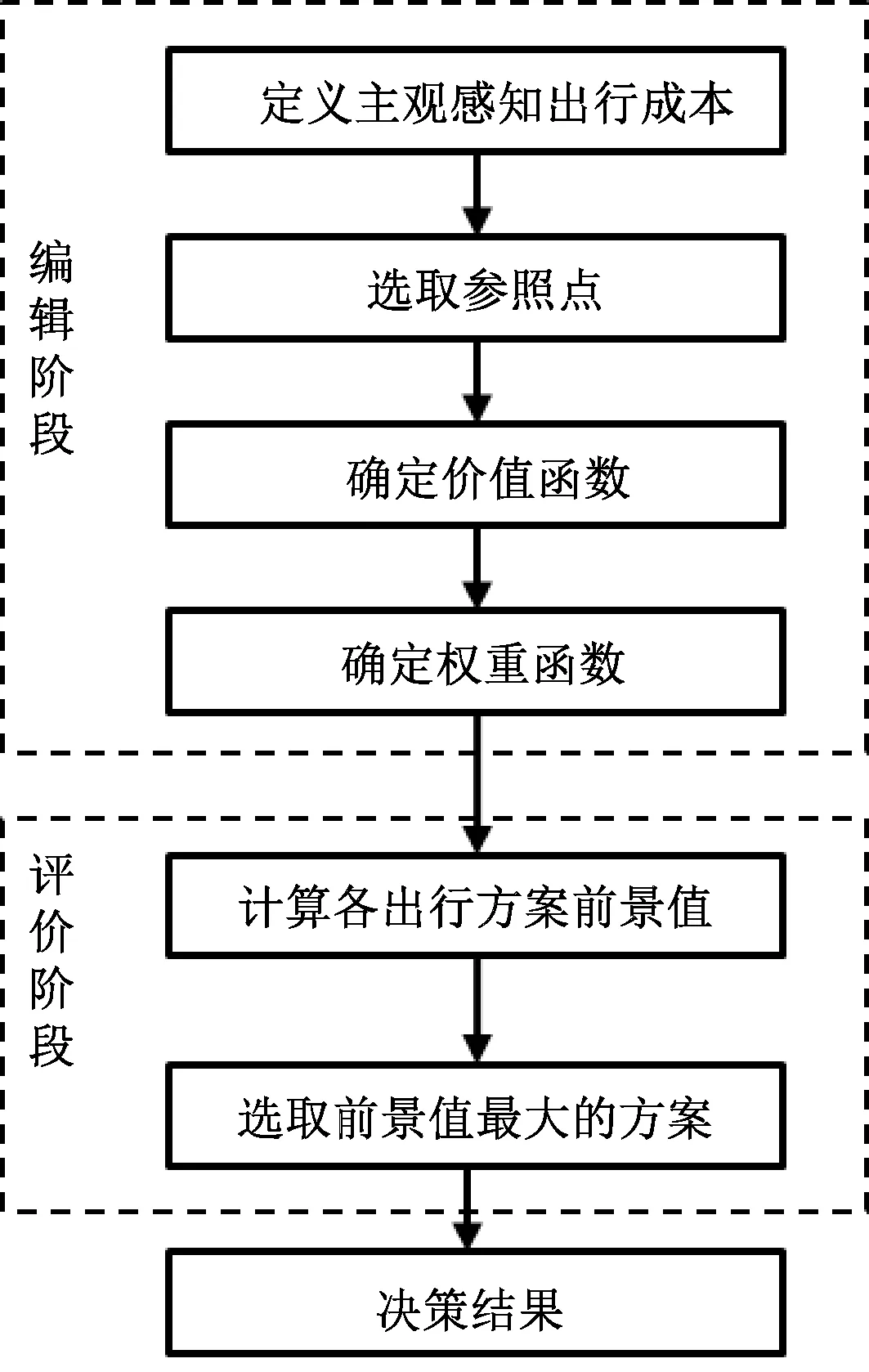
图1 前景理论的建模步骤Fig.1 The modeling steps of prospect theory

2 基于前景理论的出行决策建模过程

2.1 考虑交通政策的主观感知出行成本

出行方式的主观选择是一个复杂的心理活动，受到出行者个体属性和外界环境的共同影响。为了方便研究，将地铁、公交划分为公共交通；考虑私家车、出租车个性化的运输属性会降低道路使用率，划分为私人交通。为了提高公共交通的分担率，本文考虑两种交通政策，对公共交通实施票价折扣政策，对私人交通实施拥堵收费政策。

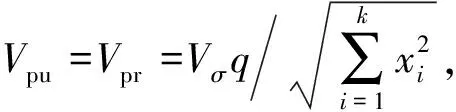
针对私人交通和公共交通，考虑不同政策下的出行方式选择，定义主观感知出行成本包括货币成本Uc、时间成本Ut、拥堵成本Uf三个部分。

2.1.1 公共交通的主观感知出行成本

本文中公共交通指公交和地铁，对其实施票价折扣政策，则出行成本包括票价、时间成本和拥挤成本。与以往研究相比，做的改进是增加了票价折扣费率η以体现票价折扣政策对出行决策的影响。定义的主观感知出行成本为

Upu=Uc+Ut+Uf

=ηPpu+θputpu+πd(Xpu)

(1)

式(1)中：η为公共交通票价的折扣费率；Ppu为公共交通的票价；θpu为公共交通出行时间的时间价值；tpu为公共交通的出行时间；π为公共交通不舒适度的单位成本；d(Xpu)为拥挤度函数，拥挤程度取决于需求量。公共交通空间的拥挤度是乘客对乘车舒适度的一种空间主观感受，也是影响出行决策的重要因素，因此拥挤成本不容忽视。

采用关于出行人数的二次函数形式对公共交通进行拥挤成本评估[14]，即

(2)

式(2)中：m,n为拥挤度函数的参数。

2.1.2 私人交通的主观感知出行成本

对私人交通实施拥堵收费政策，出行者选择私人交通的出行成本包括停车费和燃油费、时间成本以及收取的拥堵费用。引入了货币成本和拥堵收费乘数μ，考虑拥堵收费政策对出行选择的影响。因此，私家车、出租车的主观感受出行成本为

Upr=Uc+Ut+Uf

=Uc+θprt(Xpr)+uPpr

(3)

式(3)中：Uc为货币成本，私家车是停车费和燃油费，出租车是乘车费用；θpr为私人交通出行时间的时间价值；t(Xpr)为私人交通的出行时间，表示出行时间是关于交通流量Xpr的函数；μ为拥堵收费乘数；Ppr为私人交通的拥堵收费。采用广泛使用的美国联邦公路局的BPR函数计算出行时间阻抗函数，即

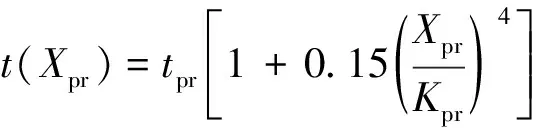
(4)

式(4)中：tpr为私人交通在路段的自由流行驶时间；Kpr为道路通行能力。出行时间随交通量Xpr的增大而递增，并未限制交通量的取值范围，因此不能表示拥堵状态下的实际出行时间。

2.2 选取参照点

参照点是一种评价标准，也是直接影响出行者选择决策结果是“收益”或“损失”的唯一指标。目前很多研究都以出行者期望的出行成本作为参照点，假设出行者具有相同的参照点，但在实际出行中，出行者往往是衡量其出行成本U对比其他交通方式的期望出行成本是收获还是损失进行决策的。因此本文中参照点的设置以其他交通方式的期望出行成本作为依据，将其他交通方式的期望出行成本加权平均得到参照点ED(U)。即令ΔU=ED(U)-U，当ΔU>0时，结果为“收益”；当ΔU<0时，结果为“损失”。将出行成本的均值分为公共交通E(Upu)和私人交通E(Upr)两类，并进行计算[13]。

公共交通的期望出行成本为

E(Upu)=ηPpu+θputpu+πE[d(Xpu)]

=ηPpu+θputpu+

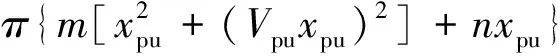
(5)

私人交通的期望出行成本为

E(Upr)=Uc+θprE[t(Xpr)]+uPpr

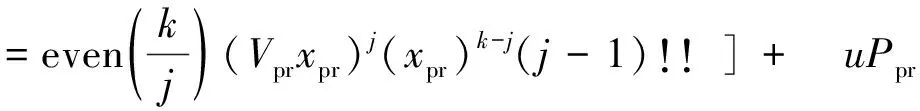
(6)

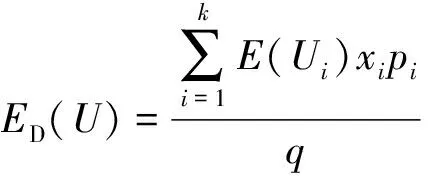
(7)

式中：even()表示沿绝对值增大方向取整后最接近的偶数，如even(1.5)=2、even(-1)=-2；p为各个出行方案可能出现结果的个人主观概率；i为其他交通方式的种类。

2.3 确定价值函数

价值函数v(U)是一种描述各交通方案对决策者所具备的价值的函数，它通过将出行者的主观感知成本与设定的参照点相对比，将出行成本转化为感知价值函数。把决策结果区分为“收益”或“损失”，并按区间的不同分别赋予各自价值的函数形式。

根据价值函数的特点以及参照点的选取，交通方式的价值函数具体表达式为

(8)

式(8)中：α1和α2为风险态度系数，α1表示收益情况下的风险规避程度(0<α1<1)，α2表示损失情况下的风险偏好程度(0<α2<1)。本文假设风险规避和偏好程度相同，即α1=α2=α。λ为损失厌恶系数，当λ≥1时表示出行者对面临损失的规避程度要大于面临收益时的追求程度，出行者对损失比收益更加敏感。

不同风险态度系数下的价值函数曲线如图2所示。

图2 价值函数曲线(α不同)Fig.2 Value function curve (different α)

图2显示了风险态度系数对价值函数的影响，根据图中各曲线的形状可以发现，价值函数的图像呈“S”形曲线，且在收益区间比损失区间的曲线斜率小。因此，在相同条件下，人们面对收益时是厌恶风险的；面对损失时是偏好风险的。α的值越接近于1，函数曲线越接近直线，表示决策者的风险倾向程度越大；值越接近于0，函数图像曲率越大。综上所述，本文假设选择私人交通方式的人群与选择公共交通的出行者对出行成本的敏感度相同，标定α=0.7。

不同损失厌恶系数下的价值函数曲线如图3所示。

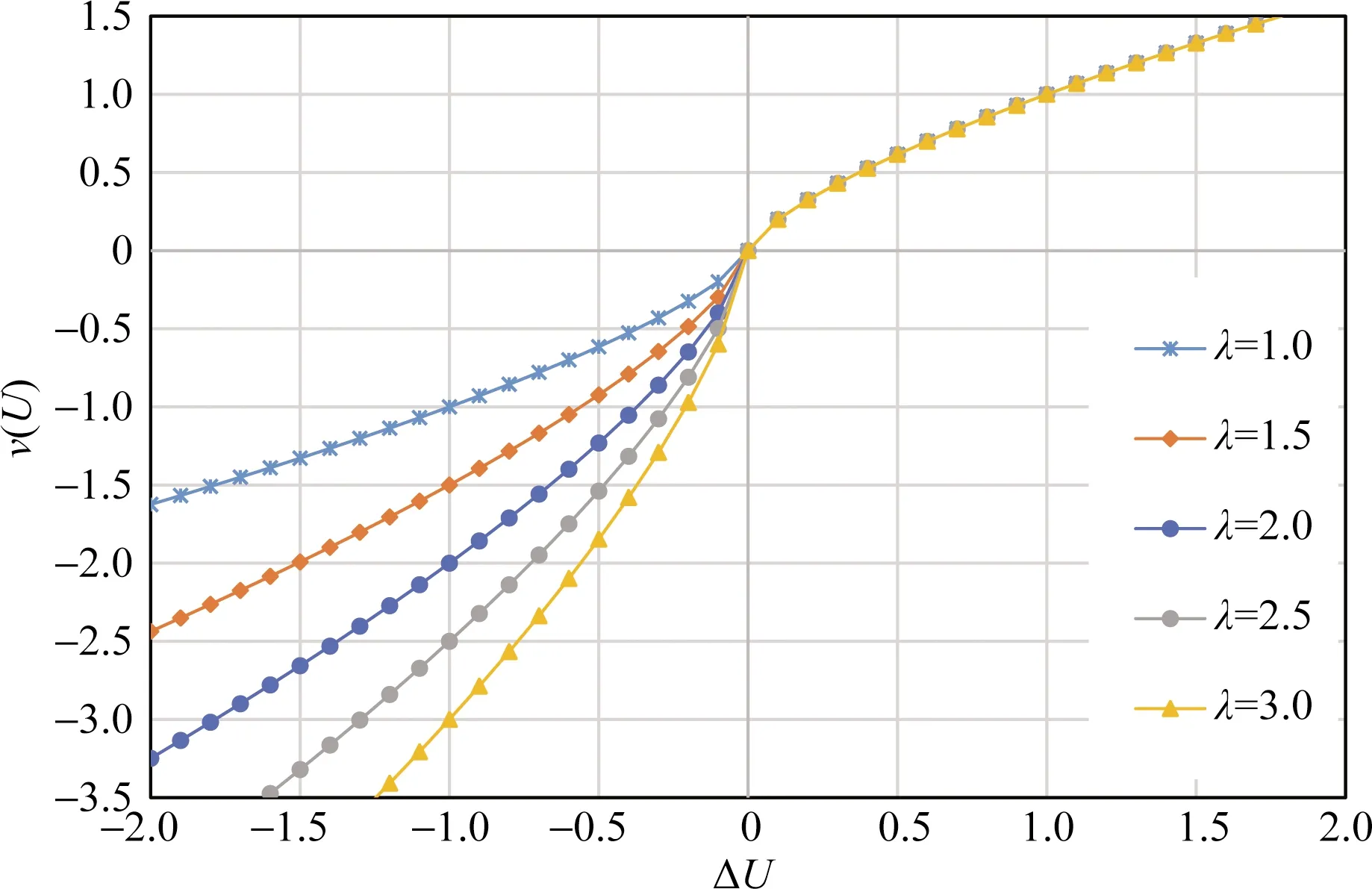
图3 价值函数曲线(λ不同)Fig.3 Value function curve (different λ)

图3展示了不同为损失厌恶系数λ下关于出行成本的价值函数的图像关系。当λ=1时，函数曲线关于ΔU=0的点对称，表示决策者对面临损失的规避程度与面临收益时的追求程度相同。通常情况下λ>1，决策者对损失比收益更敏感，这是由决策者面对风险的态度特性决定的。根据文献[15]的实验结果，标定λ值为2.25。

2.4 确定权重函数

权重函数是决策者对出行方案可能出现的结果做出的主观感知判断函数，以不确定事件发生的概率表示效用权数，将客观概率p转变为主观决策权重w(p)。

目前使用最广泛的概率权重函数的表达式为

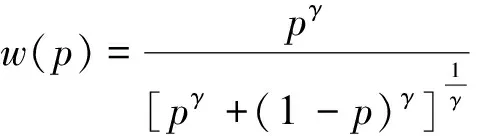
(9)

式(9)中：p为实施各个方案可能出现结果的个人主观概率，在实际出行选择行为中，概率p是决策者通过自身的经验感知判断得到的；γ为风险态度系数。

图4描述了不同参数γ下概率与权重函数的关系。由图4可知，w(p)呈倒S形。一般而言，0<γ<1，因此概率权重函数可以扩大小概率事件的影响，缩小大概率事件的影响。为了贴近实际情况，估计参数γ=0.6。

图4 权重函数曲线(不同γ)Fig.4 Weighting function curve (different γ)

2.5 前景值计算与出行决策

前景值的计算是将价值函数和权重函数结合，将出行方式的主观成本与参照点的期望成本做对比，当ΔU>0时，代表结果为“收益”，前景值为正，当ΔU<0时，代表结果为“损失”，前景值为负，出行方式前景值的计算公式可综合表达为

PVi=∑w(pi)v(xi)

=∑w+(pi)v+(xi)+∑w-(pi)v-(xi)

(10)

可能所有w(pi)v(xi)的结果都是收益，也可能所有的结果都是损失，或者是收益和损失的混合。当k种出行方式的前景值都计算出来后，出行者选择其中前景值最大的作为最佳出行方式，则第i种出行方案的前景值为

PVi=max[PV1,PV2,…,PVk]

(11)

3 不同交通政策下决策结果分析

依据某城市交通出行成本的实际情况，通过一个算例对上述模型进行验证。设置公共交通出行时间的时间价值θpu=0.2元/min，不舒适度的单位成本π=0.01，公交车的拥挤成本系数m、n取值分别为0.04和0.25，地铁由于运量更大，取值0.03和0.25；私人交通的时间价值θpr=0.3元/min，私人交通在路段的自由流行驶时间tpr=15 min，道路通行能力Kpr=600辆/15 min，私家车的拥堵收费乘数μ=1，而出租车与私家车不能一概而论，设定拥堵收费乘数μ=0.8。需要指出的是，这些参数可能并不符合实际情况，但是说明了本文模型所需的逻辑。

定义4种主要交通方式的属性如下(包括行程时间及其分布概率、货币成本)。

方案一私家车方便舒适，但易造成拥堵，停车既会花费时间还要支付停车费，主观感知出行时间70%的概率为18 min，30%的概率为28 min，出行过程中产生的货币成本为10元。

方案二出租车与私家车类似，但无需寻找停车位，步行和等车需要花费时间，预估80%概率在20 min到达，20%的概率在30 min到达，需支付乘车费用14元。

方案三公交车虽开设了公交专用道，但沿途需要停靠站点且行驶速度较慢，客流高峰期不确定性较大，预计90%的概率30 min到达，10%概率45 min到达，票价2元。

方案四地铁方式出行最稳定，线路和时间较为固定，受外界环境影响的可能性较小，高峰期舒适性较差，25 min到达的概率为100%，票价4元。

下面采用本文方法对决策者在多种交通方式中的选择行为进行分析，由于交通政策会对决策结果产生影响，因此分析不同交通需求管理措施下出行者的决策行为。

3.1 政策一：不同拥堵收费标准对出行决策的影响

结合上文建立的出行方式选择模型，若政府仅对私人交通出行者收取不同标准的拥堵费用，不给公共交通出行者票价补贴。决策原则是选择前景值最大的作为决策结果。

表1显示随着拥堵收费增加，私人交通出行者的前景值逐渐减小。当不实施任何政策时，决策结果为私家车。当拥堵收费为8元时，出行者由私家车转向出租车；当拥堵收费为25元时，由出租车出行转变为地铁出行，此时由于拥堵收费导致私人交通的出行成本越来越高，出行者更倾向选择公共交通出行。由此可知，拥堵收费达到不同额度时，出行决策的结果不同。拥堵收费是通过增加私人交通出行成本来影响出行者选择意愿的，因此私人交通对这种政策更为敏感，相对而言公共交通的前景值变化不大。

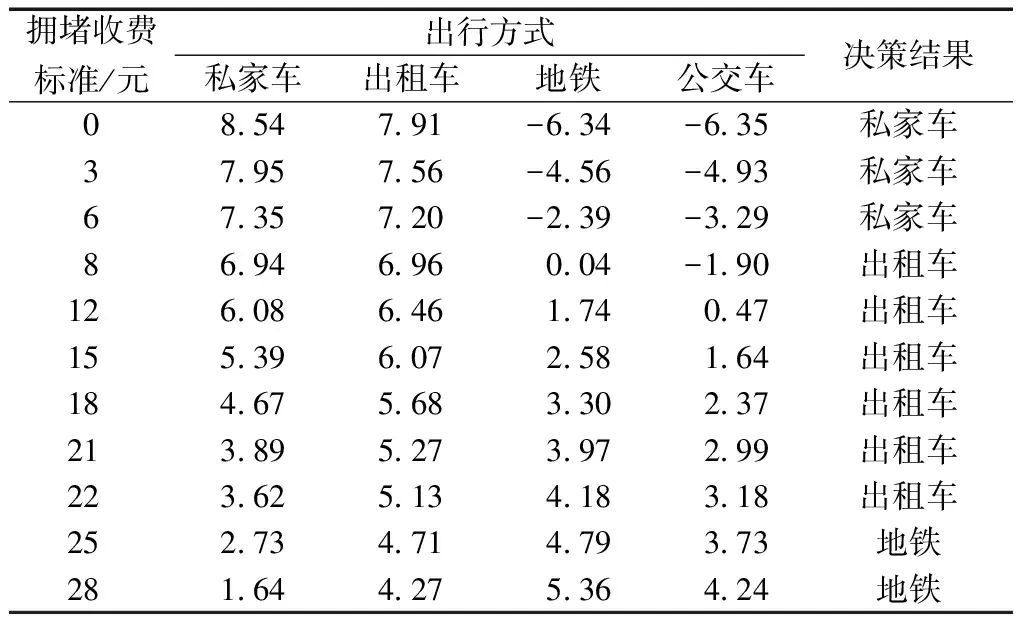
表1 不同拥堵收费标准下各种出行方式的前景值 和决策结果

3.2 政策二：不同票价折扣费率标准对出行决策的影响

结合上文建立的出行方式选择模型，若政府对私人交通不收取拥堵费用，仅对公共交通出行者补贴不同的票价折扣。

表2表明随着票价折扣费率降低，公共交通票价减少，因此总体上公共交通的前景值是增加的。由于地铁的票价比公交高，前景值的增加尤为明显，其对票价的变化更敏感。但票价折扣对私人交通出行者出行决策的影响非常小，一方面，公共交通票价只是影响主观感知成本的一部分，由于票价水平并不高，所以票价折扣费率对决策结果影响不大。另一方面，对于保有私人交通以及能够接受私人交通出行费用的出行者来说，对于地铁、公交票价的主观感知并不强烈，所以在决策结果上，私人交通用户很难因为票价折扣费率的改变发生从私人交通到公共交通的转变。可以说，折扣费率政策并未触及其痛点，这也决定其最终的选择依旧是私人交通的主要原因。因此总体上来看，票价折扣费率降低并未对决策结果造成影响，出行者依然倾向选择私人交通出行。

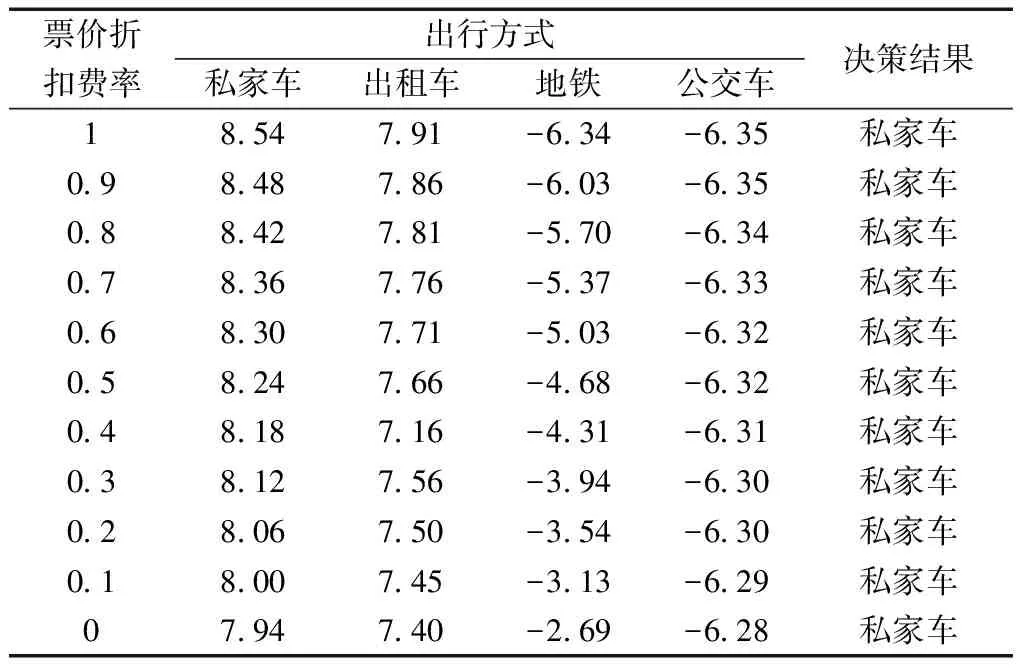
表2 不同票价折扣费率标准下各种出行方式的前景值和 决策结果

3.3 政策三：引进拥堵收费和票价折扣政策对出行决策的影响

结合上文建立的出行方式选择模型，政府同时对私人交通出行者收取不同的拥堵收费，对公共交通出行者返还票价。

由表3可以清楚地看到，随着票价折扣费率降低和拥堵收费增加，私人交通出行的前景值逐渐减小，公共交通的前景值逐渐增大，表明决策者的出行态度发生转变。当拥堵收费为8元时，出行者由私家车转成出租车；当拥堵收费为22元时，出行者不再选择私人交通，而是选择公共交通，由出租车出行转变为地铁出行，这也是实际中拥堵收费制定标准的关键。

分别对有拥堵收费无票价折扣、无拥堵收费有票价折扣、有拥堵收费有票价折扣三种交通需求政策干预下各种交通方式的前景值进行分析可知，拥堵收费和票价折扣政策对出行决策结果产生了显著影响。三种政策的对比结果表明：出行者对不同政策的敏感程度不同，拥堵收费较票价折扣政策对决策结果的影响更显著。对于有拥堵收费无票价折扣政策，出行者的出行选择由私人交通转变为公共交通的临界值为25元；无拥堵收费有票价折扣政策表明仅改变票价折扣费率不会对私人交通偏好者的选择结果造成大的影响；而对于同时引进拥堵收费和票价折扣政策，拥堵收费超过22元时，出行者就会选择公共交通，较有拥堵收费无票价折扣政策的拥堵费用标准降低了3元。

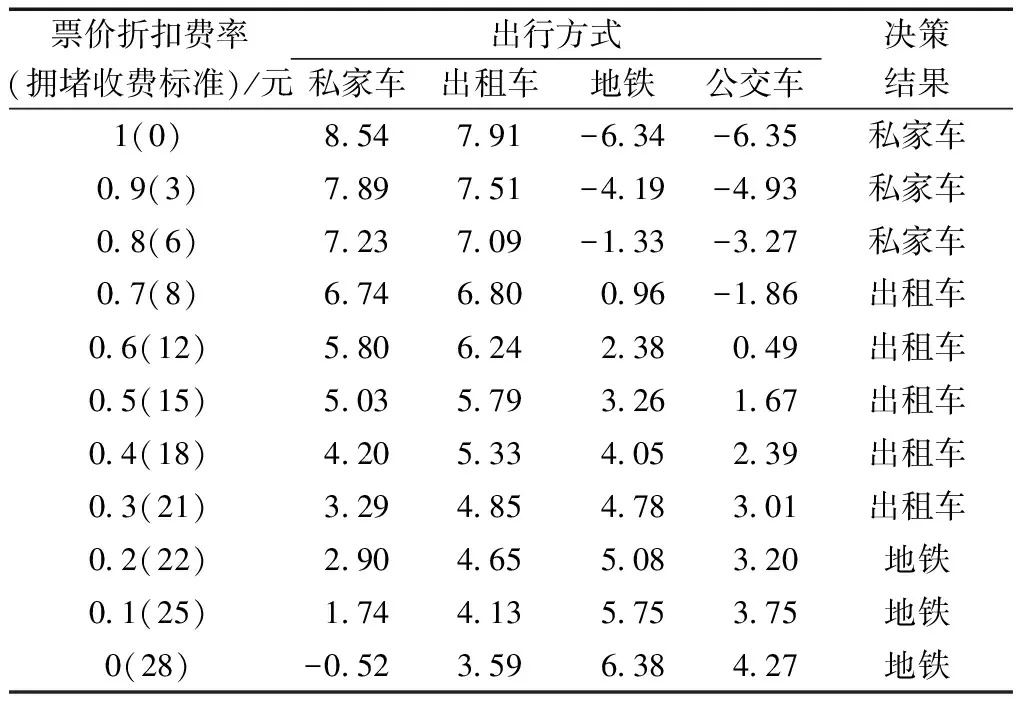
表3 引进拥堵收费和票价折扣政策的各种出行方式的 前景值和决策结果

4 结论

运用前景理论分析了出行者的出行决策行为，将出行方式划分为公共交通和私人交通两类，在此基础上建立了出行方式选择模型。与以往的相关研究相比，考虑了拥堵收费和票价折扣政策对决策行为的影响，选取其他交通方式期望出行成本的加权平均值作为参照点，并对价值函数和权重函数的参数取值进行分析和调整，提高模型的预测效果。最后通过算例验证了模型的有效性，对比分析了拥堵收费和票价折扣政策实施前后，不同政策标准对出行者出行方式选择产生的影响程度。结果表明，综合考虑实施拥堵收费和票价折扣政策情形下的基于前景理论的出行方式选择模型能有效引导居民更多的选择公共交通出行，缓解城市交通拥挤。希望能通过本文研究为城市相关部门制定合理的政策标准提供参考依据，稳定既有公共交通出行人群的同时吸引更多私人交通出行者也转向公共交通，从而缓解城市道路拥堵所带来的压力。