基于网格框架的非结构附面层网格生成技术

王 硕， 庞宇飞， 肖素梅， 刘 杨， 齐 龙， 何雨阳， 谢冬香

(1.西南科技大学 制造科学与工程学院,绵阳 621010； 2.中国空气动力研究与发展中心 空气动力学国家重点实验室,绵阳 621000)

1 引 言

随着计算机科学的发展，计算力大幅度提高，使得计算流体力学(computational fluid danamics)在各个行业中变得越来越重要，而网格生成在CFD中扮演着重要的角色，且是数值计算的重要步骤。网格中附面层网格是为了更好地捕捉近物面薄层的流动物理特性，影响着CFD计算的精度。目前生成附面层网格的自动性及可靠性较差，而且需要大量的人工交互来完成，使得附面层网格的生成费时费力。近年来，很多学者采用混合网格的策略生成半结构化的棱柱网格，以完成附面层网格的生成[1-5]。

前沿层进法[6-10]为经典附面层网格生成方法。该方法先选取物面网格为前沿层，然后基于该前沿层逐层沿法向推进，生成的网格作为前沿层，继续重复上述操作。文献[11]基于前沿层进法，发展了一套附面层网格生成方法，其中包括前沿法向和附面层生成高度的调整方法。

张来平等[12]针对附面层三棱柱网格进行了研究，提出了一种聚合的方法。首先生成各向异性的四面体网格，然后再将四面体网格进行聚合，从而生成三棱柱网格。但是聚合后会有少数质量较差的网格单元。孙岩[13]提出一种交互式棱柱网格生成方法,通过人工交互生成附面层边界点的空间推进网格，然后利用径向基函数插值方法，得到附面层每一层内部的网格点。该方法利用人工交互生成边界点作为约束条件，有效避免了附面层网格交叉，并可以对局部网格进行调整，最终生成高质量的棱柱网格。但该方法需要人工交互生成附面层网格的边界，且附面层推进过程中会存在一定的误差，需要后期进行优化。孙岩等[14]提出了一种基于约束框架的棱柱网格生成方法。首先，利用TFI(Transfinite Interpolation)生成粗背景结构框架网格，再通过背景网格和表面网格的对应关系插值得到附面层网格。该方法在附面层网格质量控制和局部修改方面有较高的效率和显著的优势，但背景框架网格生成比较困难。Lu等[15]提出一种结构多块附面层网格自动生成技术,是一种由外而内的附面层网格生成技术。首先，从表面网格中提取几何特征，再基于几何特征构造附面层网格框架，然后在框架约束内通过TFI生成结构附面层网格。该方法能够快速生成结构附面层网格，但结构网格的生成由于需要进行网格拓扑设计，不仅费时，且对软件使用者的经验有一定要求。

本文在前文的研究基础上，针对非结构附面层网格生成的自动性和局部网格质量控制能力进行研究，提出了一种棱柱附面层网格生成方法。

2 附面层棱柱网格生成方法

本文发展了文献[15]的以分而治之的附面层网格生成思想，用构造的方法生成非结构附面层网格。该方法生成的网格精度和全局一致性较高，能够有效避免复杂外形附面层网格局部及全局交叉现象。

2.1 方法思路

引进自动化的表面网格分片算法[16]，自动将表面网格分成区域可控的多个网格面片，并以此生成多块网格框架；利用结构网格附面层自动生成技术[15]的框架线算法，并加以改进，利用径向基函数插值[17]方法生成框架线中的轮廓线；在框架线的基础上，利用径向基函数插值方法构造附面层顶面网格；通过线性插值生成附面层顶层网格点与表面网格点之间的附面层内部网格点，进而生成附面层网格。避免了文献[13]在外形变化剧烈的复杂条件下，精细附面层网格生成的插值精度扰动抑制难题。图1为附面层网格生成算法的流程。

图1 附面层网格生成示意图

2.2 径向基函数插值

径向基函数插值在动网格中已经有较好应用。该方法通过选取基点之间的距离构建插值基，能够适应复杂边界。径向基函数插值的一般表现形式为[18]

(1)

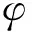
根据式(1)得到关于插值系数αi的线性方程组，表示成矩阵的形式为

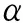
(2)

求解矩阵方程(2)可以得到插值系数αi。然后通过式(1)能得到任一点r的函数值及位移。

2.3 生成流程

算法的详细说明如下。

(1) 输入表面网格R。

(2) 支撑线的生成。按照一定的几何特性选取部分边界点作为支撑点，如图1(a)选取A，B，C和D四个支撑点。按照网格点的法向方向和输入的附面层高度h，算出支撑线AE，BF，CG和DH。可以通过平均支撑点周围网格单元的法向得到每个支撑点的法向方向，

(3)

式中np为支撑点的法向方向，Nf为支撑点p相邻网格单元总数，ni为第i个网格单元的法向。

该方法在个别点法向生成存在一定问题，这是附面层生成求法向所面临的共同难题。

(3) 轮廓线的生成。定义径向基函数插值的被插值函数f(r)为选取基点的位移，r为表面网格边界点。点A和点B的位移变形量为h，将点A和点B作为径向基函数插值的基点，首先计算出插值系数αi，然后将线AB上的非支撑网格点进行插值计算，得到线AB上非支撑网格点的位移变形量，从而得到EF上对应的网格点。同理得到FG，FH和HE上对应的网格点，生成轮廓线上的网格点Ro。

对比文献[15]轮廓线的生成是线性连接两个相邻的支撑线端点，这需要较好的网格边界。而本文方法可以处理比较复杂的网格边界的轮廓线生成，对网格拓扑要求较低。

(4) 附面层顶层网格点的生成。求解插值系数αi时，径向基函数插值中f(r)为表面边界网格点的位移ΔR，r为表面网格边界点，已知N个边界点Rb为基点，边界点的位移变形量为

ΔR=Ro-Rb

(4)

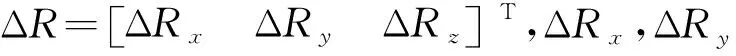
利用径向基函数插值可以得到求解插值系数的线性方程组

ΔRx=Mαx， ΔRy=Mαy， ΔRz=Mαz

(5～7)

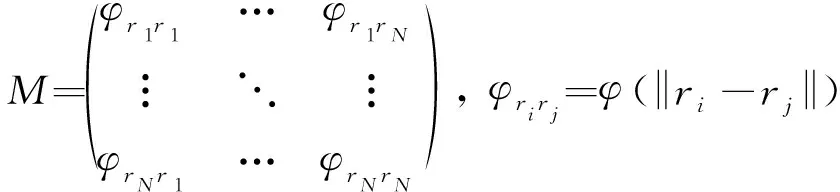
在求解表面网格内部点的位移时，被插值函数f(r)为待求值，内部网格的位移表示为ΔV。

ΔV=Dα=DM-1ΔR=HΔR

(8)

式(8)写成矩阵的形式为

(9)

求解矩阵方程(9)计算出表面网格内部点的位移值ΔV，然后得到附面层顶层网格点Rt。把表面网格点的拓扑关系映射到附面层顶层网格点上，得到附面层顶层网格的拓扑关系，生成附面层顶层网格。

(5 )附面层内部网格点的生成。连接RtR，将其按照一定的增长率分成k份，得到内部网格点Rp，通过表面网格拓扑关系和附面层顶层网格的链接关系，生成三棱柱附面层网格。

2.4 算法测试

图2所示为法向推进法和构造法的二维算法。图2(a)表明法向推进法在局部因推进过高会出现网格交叉的现象，一般通过降低附面层高度来避免，而图2(b)通过框架线的约束，能有效解决此问题。

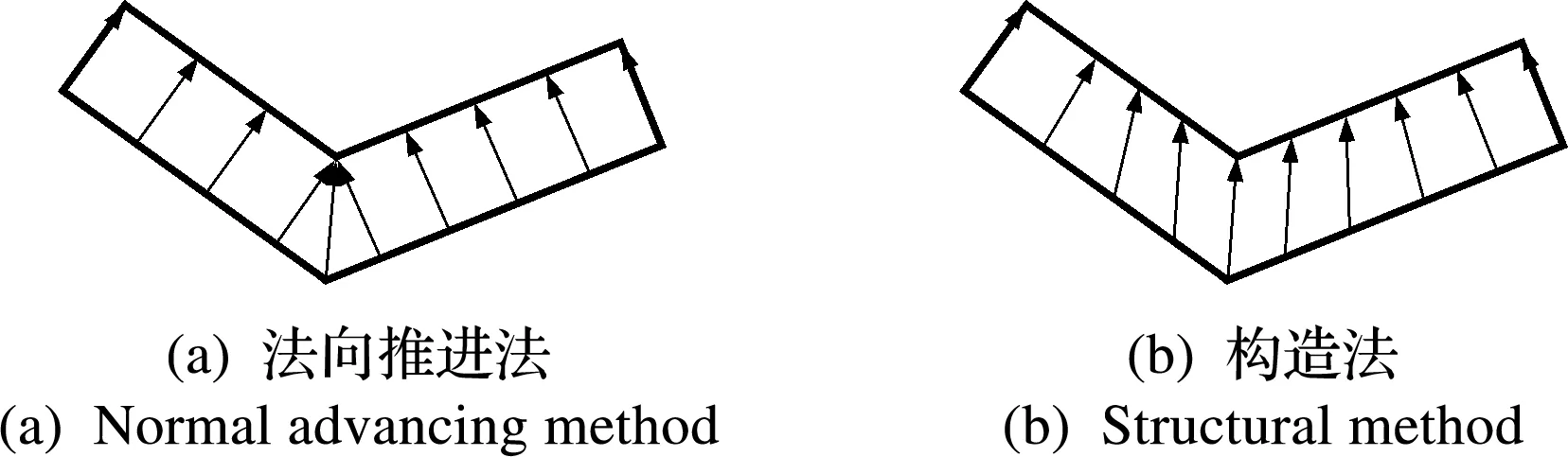
图2 法向推进法和构造法

3 算例验证

通过4种典型几何外形验证本文提出的附面层网格生成方法，分别是V型槽、圆球、吊舱和F6机翼。测试在3.5 GHz主频、16 GB内存的计算机上进行。

3.1 V型槽

V型槽是各种几何形体中的一种常见结构。如飞行器的机翼与机身连接处等。图3为V型槽的附面层网格，图中V型槽槽底附近的附面层网格不是沿着法向生长，而是在框架线和附面层顶层网格的约束下，沿着与法向有一定角度的方向生长，保证了附面层网格生成时不会出现交叉现象。

V型槽表面网格共有1074个网格点。设置20层附面层层数、0.001 mm的首层高度和1.2的增长率。附面层的网格单元最小角为22.5°，最大角为135.3°，生成时间为0.4 s。

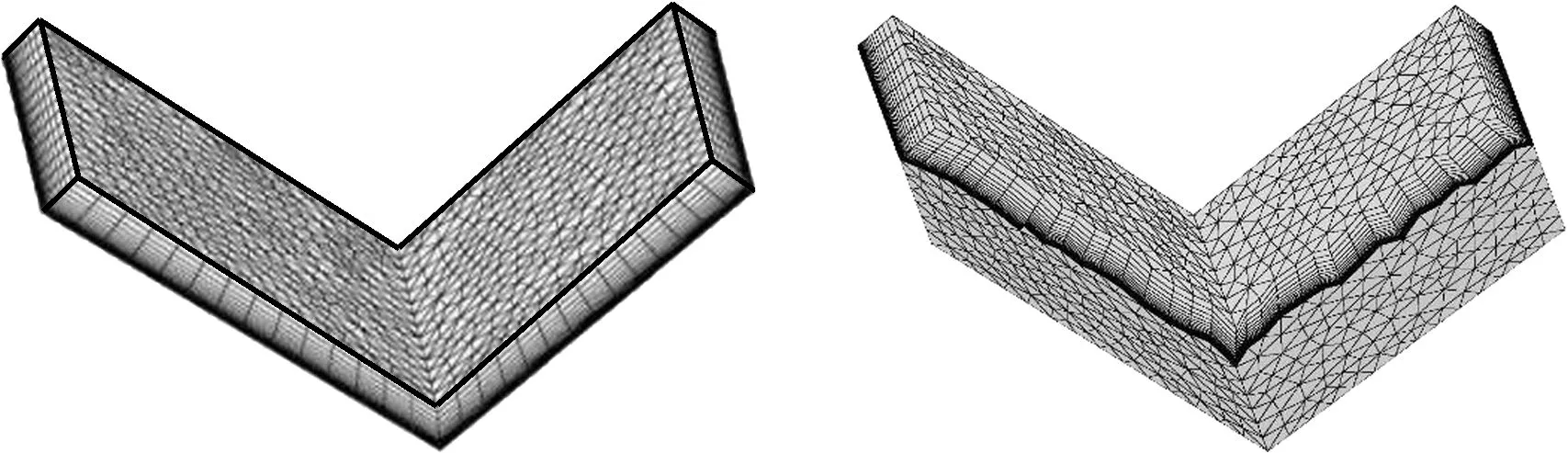
图3 V型槽的附面层网格

3.2 圆球

球面是最基本的几何曲面。图4所示为圆球的附面层网格，可以看出附面层网格的正交性较好，整体附面层网格质量较好。

圆球表面网格共有5024个网格点。设置20层附面层生长层数、0.001 mm的首层高度和1.2的增长率。附面层的网格单元最小角为25.4°，最大角为124.3°，生成时间为1.2 s。

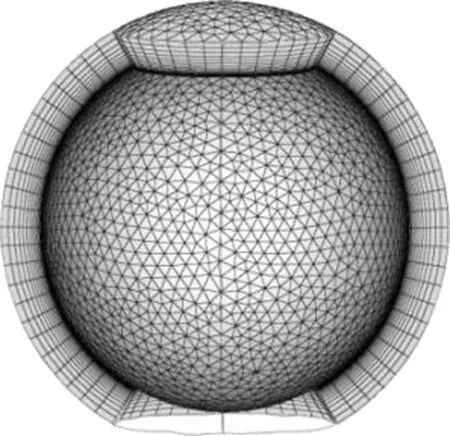
图4 圆球的附面层网格

3.3 吊舱

吊舱是外凸面和内凹面都存在的几何形体。前缘是环形的凸曲面，后缘是个环形薄片。图5(a)为吊舱表面网格和轮廓线。图5(b,c)分别为吊舱的切片图，图5(d)为局部切片图。从图5(b～d)可以看出，采用本文方法生成的附面层网格，在吊舱特殊位置处，有效地避免了附面层网格生成过程中网格点法向量交叉的问题，提高了附面层网格质量。

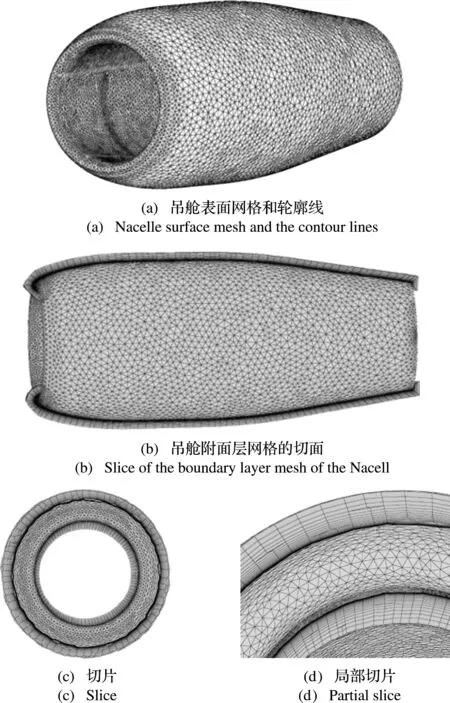
图5 吊舱的附面层网格

吊舱表面网格共有19097个网格点。设置20层附面层生长层数、0.001 mm的首层高度和1.2的增长率。附面层的网格单元最小角为6.5°，最大角为171°，生成时间为21 s。

3.4 F6机翼

图6(a)所示为F6机翼的表面网格和轮廓线。图6(b)为F6机翼附面层的切片图。图6(c)为F6局部切片图。从图6(b,c)可以看出，通过本方法进行附面层网格生成，在F6机翼的前后缘以及机翼边界处，可以有效避免利用法向推进法带来的法向交叉问题。因为本方法选取少数网格点作为基点进行法向生成，所以避免了交叉现象，较好地提高了网格质量。

图6 F6机翼的附面层网格

机翼表面网格共有12970个网格点。设置20层附面层生长层数、0.001 mm的首层高度和1.2的增长率。附面层的网格单元最小角为5.2°，最大角为161°，生成时间为31.4 s。

4 结 论

本文提出了一种基于框架的附面层棱柱网格生成方法，并通过几种典型外形对该方法进行了测试，成功生成了附面层网格，得到以下结论。通过构建的框架线和附面层顶层网格点对附面层内部网格点的约束，有效避免了附面层网格的交叉现象，保证了附面层网格的生成；表面网格发生变化时，仅需要对发生变化的局部区域重新生成附面层网格，即可快速重新生成整体的附面层网格，大幅降低了修改附面层网格的时间；大量减少了人工交互的工作，为进一步附面层网格生成自动化提供了参考。

本文在生成附面层内部的网格点时，运用了简单线性插值。表面网格形状比较复杂的时候，会造成附面层网格正交性较差的现象。将复杂的表面网格进行合理网格分区,达到复杂表面网格简单化的目的，或者选择一种合适插值方法能有效地解决这个问题，下一步工作将进一步尝试和完善。