双均值逼近屈服准则解析含腐蚀缺陷管道爆破压力
邓 磊, 章顺虎, 覃诗卉, 刘欣滢
(苏州大学 沙钢钢铁学院,苏州 215021)
1 引 言
随着现代工业的迅速发展,管道在石油和天然气的运输中起着重要作用。随着我国西气东输和川气东送等重大工程的实施,各大单位对管道的技术要求也越来越严苛,既希望可以提高管道的安全性,同时也期望尽可能发挥材料的承载能力以节省材料。因此,准确预测管道的爆破压力对于管道的选材、结构设计以及安全评估具有重要意义。
需要指出的是,长时间服役的管道,将不可避免地会出现腐蚀缺陷,使得自身承载能力下降。在此方面,国内外开展了不少关于腐蚀管道极限压力的研究工作。Kiefner等[1]通过一系列的试验研究,提出了一种评估含腐蚀缺陷管道爆破压力的方法。其后,以Kiefner的研究为基础,美国标准协会[2]率先建立了评估含腐蚀缺陷管道爆破压力的准则,即ASME B31G准则。然而,在实际应用中发现,ASME B31G准则所预测的爆破压力远小于实际压力,预测保守。为此,Cunha等[3,4]导出了受内压作用的含腐蚀缺陷管道爆破压力的解析解。但由于忽略了管材的应变硬化效应,导致预测精度仍然不足。Ma等[5]考虑材料的应变硬化指数,基于Mises屈服准则获得了适用于含缺陷高强度钢的爆破压力解析解,但该解析解高于实验结果。
随着计算机技术的快速发展,有限元模拟因其具有解决复杂问题的能力得到广泛应用。Yang等[6]使用有限元法模拟出了含沟槽形缺陷管道爆破压力的数值解。该数值解与实测值较接近,具有一定的精度。Yeom等[7]利用非线性有限元法模拟了包含单个腐蚀缺陷的管道,建立了爆破压力的评估方程。与试验结果比较发现,该评估方程具有较高的预测精度。罗懿[8]借助ANSYS Workbench软件,模拟了含有不同形状缺陷管道的等效应力,分析了缺陷参数对管道失效压力的影响。然而,需要指出的是,以上有限元模拟只能给出具体材料与结构参数下爆破压力的数值解,难以拓展到其他情况。
综合以上研究可见,含腐蚀缺陷管道的研究主要集中在数值模拟上,为数不多的解析研究还不能满足精度的要求。为此,本文拟建立一个逼近非线性Mises屈服准则的线性屈服准则,并利用该准则进行塑性极限分析,以期导出一个较为合理的爆破压力解析解。
2 双均值逼近屈服准则
2.1 新轨迹的几何描述
在π平面上,如图1所示,Mises轨迹是一个圆,Tresca为圆的内接正六边形,TSS轨迹为圆的外切正六边形。由于对称性,将其中的1/12进行局部放大,可得误差三角形OB′B,如图2所示。可以看出,上述准则的偏差应力矢量在OB′共线且模长相等,在OB上共线但模长不等。图2中,B′F和B′B分别为Tresca轨迹和TSS轨迹的边,而OF和OB′分别为Tresca轨迹和TSS轨迹的边心距。对其边和边心距的均值同时逼近,则可确定新的屈服边长B′E与边心距OI。根据这一设想,可以建立如下方差形式的数学表达式。
(1)

(2)


图1 π平面上的双均值屈服轨迹

图2误差三角形内的双均值屈服准则
(3)
x=B′E=0.415σS
(4)
于是,OE,DE,OI,EF以及∠FB′E,∠OB′E,∠OEB′,∠B′OI可确定为
(5)
(6)
由式(5,6)可知,新轨迹是一个边长为0.415σS的等边非等角十二边形,6个内接顶角为140.71°,另6个伪内接顶角为159.29°。
新轨迹与Mises弧在E点与I点的误差分别为
(7)
同时,新轨迹的周长和面积与Mises圆相比,相对误差分别为
(8)
由此可见,新轨迹居于Tresca轨迹与Mises轨迹之间,从内侧靠近Mises圆。

图3 σ1在π平面上的投影
2.2 新准则的数学表达式
根据主应力σ1在π平面上的投影关系[9],如图3所示,可得
(9)
假设A′E满足式(10),即
σ1-a1σ2-a2σ3-c=0
(10)
当材料屈服时有c=σs,a1+a2=1,将式 (9)代入式(10)可得
a1=0.191,a2=0.809
(11)
于是,式(10)可确定为

(12)
同理,轨迹B′E可确定为

(13)
式(12,13)即为新准则的数学表达式,称为双均值逼近屈服准则,或简称为DM屈服准则。该准则表明,若应力分量σ1,σ2和σ3按系数1,0.191,0.809 或0.809,0.191,1进行线性组合,则材料发生屈服。
2.3 屈服准则的验证
当约定σ1≥σ2≥σ3时,为评价中间主应力的影响,Lode[10]引入的应力参数表达式为
μ=(2σ2-σ1-σ3)/σs
(14)
将式(14)分别代入Tresca,Mises,TSS以及DM屈服准则,可得其相应的Lode应力参数转换式为
(15,16)
(17)
(18)
利用转换式(15~18),并结合已有的实验数据[10-13],可得图4所示结果。可以看出,Tresca屈服准则为实验数据的下界,而TSS屈服准则为上界;DM屈服准则介于TSS准则与Tresca准则之间,位于Mises准则下方。总体而言,DM屈服准则与实验数据较一致,提供了较为合理的中间结果。

图4 屈服准则实验结果对比
3 管道爆破压力
3.1 材料硬化模型
当管道受内压作用而超过屈服强度时,管道进入塑性状态。继续加压,管材发生应变硬化,管道的承载能力提高;同时,壁厚变薄,又使承载能力下降。当内压达到一定值后,管道将发生爆破,此时的极限内压力称为爆破压力。对此情况,通常使用幂律应变硬化曲线来描述管道的应力-应变关系[14,15]
σ=Kεn,K=(e/n)nσT
(19)
式中σ为单向拉伸时的真应力,ε为单向拉伸时的真应变,K为强度系数,σT为抗拉强度,n为应变硬化指数,e=2.71828为自然对数。
屈强比(σY/σT),即材料的屈服强度与抗拉强度的比值,决定材料的应变硬化指数。Zhu等[16]曾给出各种不同管材的拟合表达式,即
(20)
式中σY为屈服强度,σT为抗拉强度。
3.2 爆破压力
假设某一无缺陷且两端封闭的薄壁长管道,承受内部压力,其主应力可表示为[17]
(21)
式中θ,r和z代表管道的周向、径向以及轴向;D为管道瞬时直径,t为瞬时壁厚,P为管道内压。将式(21)代入式(12),可得基于DM屈服准则的等效应力为
(22)
对应的管道主应变可表示为
(23)
式中D0和t0分别为管道初始内径和初始管壁厚度。在塑性变形时,满足体积不变条件,即ε1+ε2+ε3=0,则由式(23)可得
(24,25)
根据Hill塑性功假设[18]有
(26)

将式(22)代入式(26)得
(27)
将式(27)代入式(25)得
(28)
由式(19,22,28)可得
(29)
(30)

(31)

(32)

(33)
(34)
式中f为缺陷几何形状和材料的函数,L为缺陷长度,C≈-0.157[19],R=D/2为管道半径。
联立式(20,33,34),腐蚀管道爆破压力的表达式为
(35)
从式(35)可看出,当缺陷深度比d0/t0=0时,Pd与式(30)表示的Pb相同。
3.3 对比与验证
为了验证式(35)的合理性,对比文献[5]含腐蚀缺陷X70管道的模拟结果,其中材料参数、管道几何参数以及缺陷参数列入表1。对比结果如图5所示。

表1 X70管道的几何参数和缺陷参数Tab.1 Geometirc defect and defect parameter for X70 pipeline

图5 本文爆破压力与模拟值的比较
式(35)预测的爆破压力与爆破压力模拟结果较接近,且最大误差不超过10.11%,具有较高的预测精度。
为进一步验证,也将式(35)的预测结果与已有关于X80和X100两种管线材料的实验结果[5]作了对比。同时,为反映不同屈服准则的影响,也给出了按照本文推导方法得到的Tresca准则预测值和TSS准则预测值。以表2为两种实验材料的实验条件,表3为实验值以及不同准则计算值的对比结果,其中ΔTSS,ΔTresca和ΔD M分别表示3准则计算值与实验值的相对误差。
由表3可知,使用TSS屈服准则得到的管道爆破预测值普遍偏大,而使用Tresca屈服准则的预测值则偏小。使用本文提出的DM屈服准则所得的预测值不仅介于TSS和Tresca之间,而且更加靠近实验结果,最大误差不超过12.7%,可见双均值逼近屈服准则在实际应用中具有较大的应用潜力,对于求解其他金属结构件的力学参数具有参考意义。

表2 X80和X100管线爆破实验条件Tab.2 Experimental conditions of the burst tests for X80 and X100 pipelines

表3 实验值与不同准则预测值的比较Tab.3 Comparison between the predicted value and the experimental one
4 结果与讨论
图6为式(30)在σT=614 MPa下确定的爆破压力。可以看出,当t0/D0不变时,管道的爆破压力随σY/σT的增大而增大;当σY/σT不变时,管道的爆破压力随t0/D0的增大而增大。
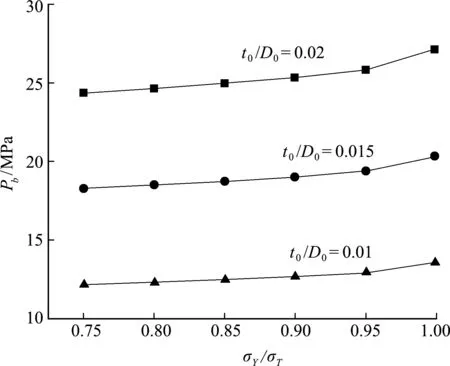
图6 爆破压力与σY/σT和t0/D0的关系


图7 爆破压力随径厚比与屈强比的变化规律
5 结 论
(1) 建立了双均值逼近屈服准则,其表达式是主应力分量的线性函数,其轨迹介于Tresca轨迹与TSS轨迹之间。在π平面上,双均值逼近屈服准则是一个边长为0.4150σS的等边非等角十二边形,顶角分别为140.71°和159.29°。通过对比发现,该屈服准则的预测结果与实验数据吻合较好,给出了较为合理的中间结果。
(2) 基于双均值逼近屈服准则对管道进行塑性极限分析,导出了含腐蚀缺陷管道的爆破压力解析解。与已有实验数据对比表明,该解析解预测的爆破压力与实验实测数值吻合较好,最大误差不超过12.7%。
(3) 影响参数的定量分析表明,爆破压力随屈强比(σY/σT)的增加而增加,随缺陷深度比(d0/t0)的增加而降低。

