一种预测层合板层间剪应力的新后处理方法
杨胜奇, 刘书田
(大连理工大学 工程力学系 工业装备结构分析国家重点实验室,大连 116024)
1 引 言
层合板是由不同材料属性的薄片通过某种工艺(如粘接)复合而成,具有轻质、参数可设计性强和比强度比刚度高等优点,广泛应用于航空航天领域。在层合板中,通常不同材料之间连接界面的力学性能最为薄弱。过大的层间剪应力会导致层合板界面处发生分层破坏。分层破坏是层合板的主要失效形式[1],如纤维增强复合材料层合板损伤失效50%以上是由分层引起[2]。因此,准确预测层合板的层间剪应力尤为重要。
现已提出了大量的层合板分析理论[3-8],如一阶剪切变形理论[3]、高阶剪切变形理论[4]和锯齿理论[5-6]等。这些理论能够准确地预测层合板的面内应力,然而大都无法直接通过本构方程获得准确的横向剪应力[9]。为了获得更准确的横向剪应力,Whitney[10]提出了三维平衡方程后处理方法(TPM),其广泛应用于层合板的横向剪应力预测[5,11-13]。然而,三维平衡方程后处理方法(TPM)需要计算面内应力的一阶导,使得简单的低阶单元无法使用TPM计算横向剪应力。以线性单元为例,其为常应变单元,面内应力的一阶导恒为零。因此,基于线性单元和三维平衡方程后处理方法得到的横向剪应力也恒为零。为了使用TPM获得更准确的横向剪应力,常使用高阶单元,如六节点三角形单元[11]、八节点四边形单元[12]和九节点四边形单元[13]。但高阶单元的使用往往会造成节点数目的增多和计算效率的降低。此外,还可以通过使用局部应变光顺[14]或局部应力光顺[15]的方法来获得面内应力的一阶导。这类方法能够使用TPM有效地获得少量节点的横向剪应力。然而,如果想要获得所有节点的横向剪应力,需要花费非常多的计算时间。因此,需要发展一种高效的新后处理方法来预测层合板的横向剪切应力。
本文提出了一种新后处理方法来预测层合板的横向剪应力。其优点在于可以使用低阶单元来预测层合板的层间剪应力。基于修正锯齿理论(RZT)[5]和新后处理方法,本文构造C0连续的三节点三角形线性板单元。几个典型算例验证了新后处理方法的计算精度以及提出板单元的计算效率和精度。
2 修正锯齿理论(RZT)
修正锯齿理论(RZT)是一种C0型锯齿理论,基于RZT,层合板的位移场[5]可表示为


w(x,y,z)=w0(x,y)
(1)

(2)

3 三维平衡方程后处理方法(TPM)
基于修正锯齿理论,直接通过本构方程得到的横向剪应力精度低。为了获得更为精确的横向剪应力,常使用三维平衡方程后处理方法。忽略体力,三维平衡方程可表示为
(3)
应用自由表面条件,由三维平衡方程得到的横向剪应力表达式可表示为
(4)
对于正交铺层层合板,可以使用两个独立的圆柱弯曲[16]来进一步简化式(4),式(4)可以重写为
(5)
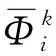
4 新后处理方法(NPM)
为了消除式(5)位移参数的二阶导,提出一种虚功等效法。虚功等效法假定由本构关系获得的横向剪应力在虚剪应变上做的功等于由三维平衡方程获得的横向剪应力在虚剪应变上做的功。基于虚功等效法,可得
(6)

将本构方程和式(5)代入式(6),可得到由新后处理方法(NPM)获得的横向剪应力的表达式为
(7)

5 C0连续的三节点三角形单元
基于修正锯齿理论和新后处理方法,构造一种有效的C0连续的三节点三角形线性板单元。对于三节点三角形单元,位移参数可以离散为
(8)
式中Li为面积坐标。
基于几何方程,单元应变向量可以表示为
ε=Bδe
(9)
式中节点运动变量参数向量δe和单元应变矩阵B分别为
(10)
B=(B1,B2,B3)
(11)
基于新后处理方法,将式(8)代入由新后处理方法获得的横向剪应力式(7),可得
(12)

6 算 例
采用不同的复合材料层合板和复合材料测试所提出的新后处理方法的计算精度以及基于该方法提出板单元的计算效率和精度。选用层合板算例的材料特性和铺层顺序分别列入表1和表2。为了便于对比研究,横向剪应力的无量纲化为

表1 材料特性(单位:GPa)
6.1 新后处理方法的计算精度评估
为了评估新后处理方法的计算精度,选取具有三维弹性解(Exact)的承受双正弦载荷的简支层合板(Laminate A)进行研究。为了避免网格密度的影响,用解析法研究新后处理方法的计算精度。基于修正锯齿理论(RZT),分别由本构方程(CE)、三维平衡方程后处理方法(TPM)和新后处理方法(NPM)得到层合板的横向剪应力,如图1所示。可以看出,新后处理方法和三维平衡方程后处理方法具有相同的计算精度。与三维弹性解(Exact)[17]对比可知,由本构方程获得的横向剪应力存在较大误差,修正锯齿理论(RZT)结合后处理方法能够获得高精度的横向剪应力。
6.2 提出板单元的计算效率和计算精度评估
本文基于修正锯齿理论(RZT)和新后处理方法(NPT)构造一种C0连续的三节点三角形单元,为了评估提出单元的计算效率,与基于三维平衡方程后处理方法的六节点三角形单元[11]进行对比。表3给出了不同网格下两个单元的节点数目和计算耗时。对于相同的网格(12×12),六节点三角形单元的节点数目是三节点三角形单元的3.7倍,六节点三角形单元的计算时间是三节点三角形单元的11.43倍。并且随着网格的加密,倍数呈现逐渐增大的趋势。本文进一步比较了在相同计算精度下两种单元的计算耗时。由表4可知,当单元的最大误差为0.8%时,三节点三角形单元网格数为20×20,计算耗时为1.74 s(表3),六节点三角形单元的网格数为12×12,计算耗时为3.20 s(表3)。通过对比可知,基于新后处理方法构造的三节点三角形板单元比基于三维平衡方程后处理方法构造的六节点三角形单元具有更高的计算效率。

图1 层合板的横向剪应力对比(Laminate A,a /h=4)
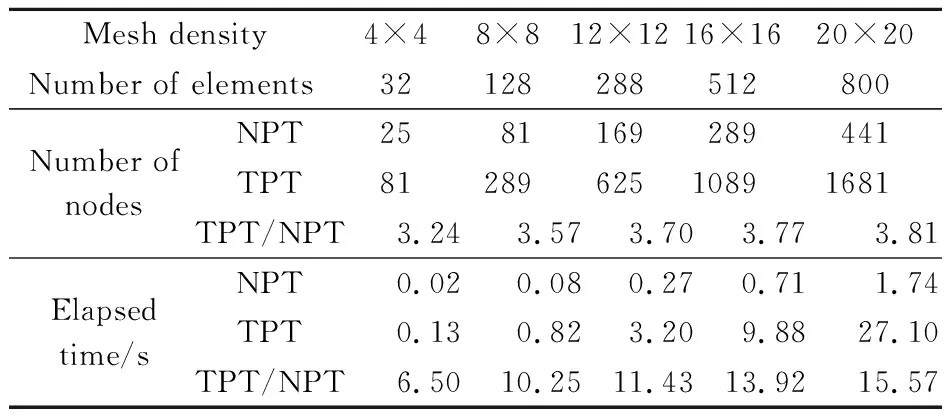
表3 两种板单元自由度数及计算时间的比较
图2和图3给出了由提出的线性板单元获得的不同夹层板的横向剪应力。Laminate B是由单层面板和芯层构成的三层夹层板,Laminate C的面板是由多层复合材料层合板构成。可以看出,提出的板单元结合新后处理方法(NPM)获得的横向剪应力与三维弹性解(Exact)[17]吻合较好,而由本构方程(CE)获得的横向剪应力具有较大误差。
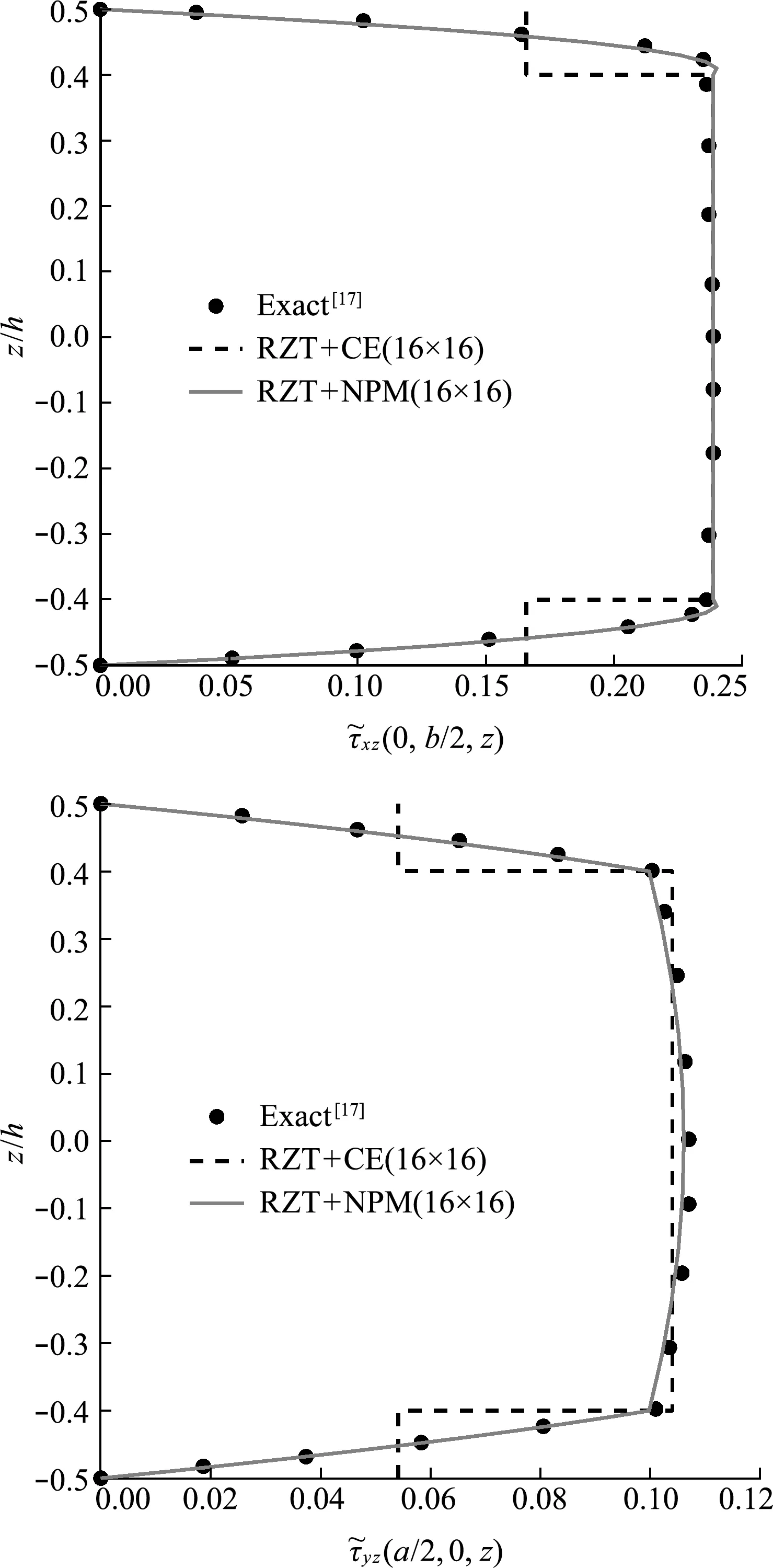
图2 三层夹层板的横向剪应力对比(Laminate B,a /h =4)

图3 多层夹层板的横向剪应力对比(Laminate C,a /h =10)
6.3 基于新后处理方法和商用软件预测层合板的层间应力
工程中常用3维单元计算层合板的层间应力,该方法存在计算效率低的缺点。而使用商用软件中现有的板壳单元,只能准确预测层合板的变形和面内应力,无法准确预测层间剪应力。由于使用新后处理方法计算层间剪应力具有无需提高单元阶次的优点。因此,可以结合商用软件和新后处理方法来预测层合板的层间剪应力。本文结合Abaqus和新后处理方法,验证上述思路的可行性。首先,基于Abaqus的S4R5薄壳单元(对应一阶剪切变形理论),获得层合板的节点位移;然后使用获得的节点位移和新后处理方法,获得层合板的层间应力。本文以承受正弦载荷(q=q0sin(πx/a))的对边简支对边自由的层合板(Laminate A)来验证该方法的精度。层合板厚度为3 mm,长和宽为 60 mm。图4给出了不同方法预测的层合板的横向剪应力。3D -FE表示由Abaqus软件使用3维单元(C3D8R)预测的结果。FSDT+NPM表示先由Abaqus软件使用薄壳单元(S4R5)获得节点位移,然后由新后处理方法获得的横向剪应力。在划分相同面内网格情况(60×60)下,3D -FE自由度数为692106,壳单元自由度为18605,3D -FE的自由度数是壳单元的37.2倍。可以看出,FSDT+NPM的预测结果与3D -FE结果和三维弹性解(Exact)[17]吻合较好,证明基于新后处理方法和商用软件预测层合板的层间应力是可行的。此外,由于针对特定单元,由新后处理方法获得横向剪应力的表达式(7)可以显式给出,新后处理方法也可以很容易集成到商用软件中。
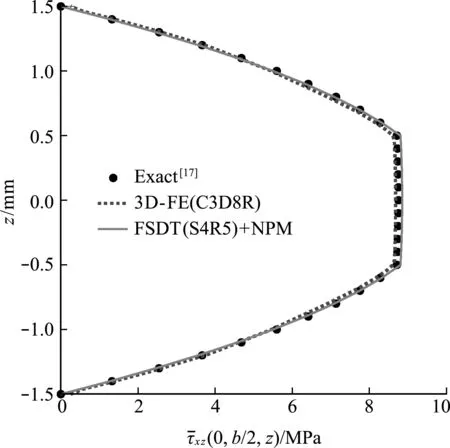
图4 层合板的横向剪应力对比(Laminate A,a /h =20)
7 结 论
为了实现使用低阶单元准确预测层合板层间剪应力的目的,本文提出了一种新后处理方法。该方法使用虚功等效法消除了三维平衡方程后处理方法中产生的位移参数高阶导,解决了三维平衡方程后处理方法无法使用低阶单元计算层间剪应力的难题。基于修正锯齿理论和新后处理方法,构造了一种C0连续的三节点三角形线性单元。通过经典算例验证了新后处理方法的计算精度以及提出线性单元的计算效率和精度,可得到如下结论。
(1) 新后处理方法和三维平衡方法后处理方法具有相同的计算精度。
(2) 基于新后处理方法和修正锯齿理论,仅使用线性单元就可以获得高精度的横向剪应力。
(3) 新后处理方法结合现有的有限元商用软件,可以高效高精度地预测层合板的层间剪应力。
附录A:
(A1)



(i=1~3)(A2)
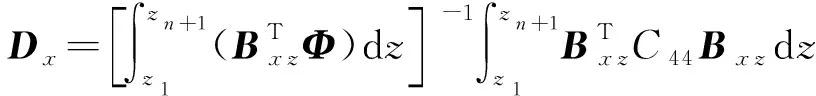

ei为三维单位列向量。

