一种新型的高分辨率通量差分裂格式

胡立军， 赵昆磊， 袁海专

(1.衡阳师范学院 数学与统计学院，衡阳 421002；2.中国科学院数学与系统科学研究院 计算数学与科学工程计算研究所，北京 100190；3.湘潭大学 数学与计算科学学院,湘潭 411105)

1 引 言

数值模拟高马赫数流动问题需要精确鲁棒的数值格式。无论在理论研究还是在工程应用中，迎风格式都是最受欢迎的激波捕捉方法。根据反映控制方程组物理特性的不同方式，通常可将其分为通量差分裂(FDS)格式和通量向量分裂(FVS)格式。流行的通量差分裂格式主要包括Roe格式[1]、Osher格式[2]和HLL-类格式[3-5]。其中，利用系统的特征值和特征向量构造的Roe格式计算代价小并且能够精确捕捉各类间断。但是，由于Roe格式不满足熵条件，故在计算中会产生非物理的膨胀激波。在计算强激波问题时，低耗散的Roe，Osher，HLLEM 和HLLC格式还会遭遇红玉(carbuncle)现象的困扰，这极大地影响了对于高超声速流动问题的精确模拟。消除低耗散通量差分裂格式激波异常现象的一些工作主要包括，与耗散格式进行混合[6-8]、对Roe格式进行熵修正[9]、构造旋转格式[10]、反扩散控制方法[11]、多维耗散方法[12]、添加人工粘性[13]以及增加剪切粘性[14]等。这些方法通过局部增加格式的数值耗散成功地抑制了激波不稳定现象，但是在计算复杂流动问题时，不合适的数值耗散可能会影响接触面和剪切层的精度。

以Steger-Warming格式[15]和van Leer格式[16]为代表的通量向量分裂方法在计算中具有很好的鲁棒性，但是其主要的缺点是不能精确分辨接触间断和剪切波。此外，基于对流-压力通量分裂方法构造的混合迎风格式也吸引了许多研究人员的关注。Liou等[17]将动量方程中的压力项分裂出来，并且构造了一种可以精确分辨接触间断的对流迎风分裂方法(AUSM)。目前，AUSM格式已经发展成为具有广泛应用前景的AUSM-类格式[18-20]。Zha等[21]将动量方程中的压力项以及能量方程中速度与压力的乘积项分裂出来进而构造了一种混合迎风格式。此外，Toro等[22]提出了一种新的对流-压力通量分裂方法，其特点是对流通量中完全不含压力项。基于对流-压力通量分裂方法构造的混合迎风格式形式简单并且能够精确捕捉接触间断，但是在计算某些问题时仍然会出现红玉现象和激波波后振荡[23]。

本文基于Zha-Bilgen对流-压力通量分裂方法来构造一种精确鲁棒的新型通量差分裂格式。压力子系统具有一组完备的线性无关的特征向量，因此可以构造传统的通量差分裂格式来进行计算。弱双曲的对流子系统采用文献[24]添加广义特征向量的方法构造通量差分裂格式来进行计算。为了提高接触间断的分辨率，利用界面变差下降(BVD)算法[25]来减小对流通量耗散项的密度差。稳定性分析和数值实验证明了新的通量差分裂格式比Roe格式具有更好的鲁棒性和更高的分辨率。

2 预备知识

二维无粘可压缩流的控制方程组可以表示为

(1)

式中

(2)

(3)

除非特别说明，否则比热比γ取1.4。将计算区域划分成结构化的四边形网格并且采用有限体积方法对式(1)进行空间离散,

(4)

(5)

Roe格式[1]数值通量的表达式为

(6)

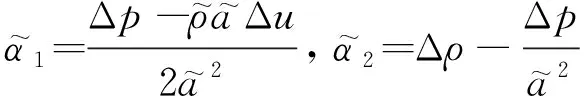
(7)

(8)

(9)

Roe格式能够精确捕捉各类间断，但是不满足熵条件，在计算中会产生非物理的膨胀激波。在计算强激波问题时还会遭遇红玉现象。

3 一种新型的通量差分裂格式

基于Zha-Bilgen分裂方法来构造一种精确和鲁棒的通量差分裂格式。

3.1 Zha-Bilgen分裂

Zha等[21]将欧拉方程的通量分裂成对流通量和压力通量两部分。

(10)

对流通量Fc的雅可比矩阵为

(11)

Ac的特征值为

(12)

其线性无关的特征向量为

(13)

压力通量Fp的雅可比矩阵为

(14)

Ap的特征值为

(15)

其线性无关的特征向量为

(16)

从式(12，15)可以看出，对流子系统的四个特征值都等于流体在该方向的速度，从而表现出很好的对流特性。而压力子系统的特征值等于声速的常数倍，很好地反映了声速波的特性。

3.2 FDS -ZB -BVD格式

3.2.1 压力数值通量

从式(16)可以看出，压力子系统有一组完备的线性无关的特征向量，因此可以构造传统的通量差分裂格式来计算压力数值通量,

(17)

(18)

(19)

3.2.2 对流数值通量

对流子系统满足微分关系式,

(20)

将式(20)改写成有限差分形式,

(21)

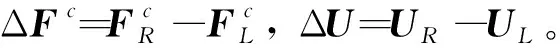
从式(13)可知，对流子系统没有一组完备的线性无关的特征向量，因此无法直接将ΔU分解成对流子系统特征向量组的线性组合。采用文献[24]的约旦标准型理论来添加广义特征向量，并且注意到对流子系统有四个相等的特征值u，可以得到：

(22)

因此，对流子系统的数值通量可以表示为

(23)

为了减少数值耗散，利用THINC函数来重构界面两侧的密度[25]，

(24)

式中ρmin=min(ρi -1,ρi +1), Δρ=|ρi +1-ρi -1|

A=[B-cosh(β)]/sinh(β)

θ=sgn(ρi +1-ρi -1),ε=10-20

(25)

数值实验表明，耗散控制参数β取1.1～2.0，都可以得到理想的结果，β越大耗散越小。后面的数值实验β均取1.5。

(26)

因此，基于Zha-Bilgen分裂方法并且结合BVD算法构造的通量差分裂格式(命名为FDS -ZB -BVD)数值通量的表达式为

(27)

本文将通过稳定性分析和数值实验来证明该格式比Roe格式具有更好的鲁棒性和更高的分辨率。

3.3 稳定性分析

低耗散的数值格式在计算强激波问题时会遭遇激波不稳定现象。采用矩阵稳定性分析方法[26]对Roe格式和FDS -ZB -BVD格式进行稳定性分析。

将计算区域[0,1]×[0,1]划分成20×20的笛卡尔网格，马赫数M0=7的稳态驻激波位于第10列和第11列网格单元共有的网格界面上。激波的上游状态为

(28)

下游状态通过Rankine -Hugoniot关系式来得到

(29)

本文研究不同格式的数值误差随着时间的发展趋势。整个区域的流场可以分解为

(30)

(31)

将线性化的通量函数代入式(4)，可以得到

(32)

将式(32)改写成矩阵形式，

(33)

式中q=20×20为网格单元总数，S为稳定性矩阵。求解式(33)，得到数值误差的演化方程为

(34)

误差发展有界的条件为

max{Re[λ(S)]}≤0

(35)

式中Re[λ(S)]表示稳定性矩阵S的特征值的实部。

图1展示了稳定性矩阵S的特征值在复平面上的分布。可以看出，本文构造的FDS -ZB -BVD格式是稳定的，而Roe格式是不稳定的。在计算强激波问题时，FDS -ZB -BVD格式会比Roe格式表现出更好的鲁棒性。第4节的数值实验也证明了这一点。

4 数值结果和分析

通过数值实验来检验FDS -ZB -BVD格式的精度和鲁棒性。采用二阶MUSCL格式获得空间的二阶精度，时间离散采用二阶Runge -Kutta格式。

4.1 一维算例

计算几个经典的算例来比较FDS -ZB -BVD格式和Roe格式捕捉间断的能力。

4.1.1 孤立的接触间断

计算马赫数M0=0.1的孤立接触间断。将计算区域[0,1]均匀划分成100个网格，初始条件为

(36)

图2展示了t=2.0时的密度分布。可以看出，FDS -ZB -BVD格式可以更加精确地捕捉该接触间断。

图1 稳定性矩阵S的特征值在复平面上的分布

图2 孤立的接触间断的密度分布

4.1.2 Lax问题

将计算区域[0,1]均匀划分成100个网格，初始条件为

(37)

该算例由一个左行的稀疏波、一个右行的接触间断和强激波构成。图3展示了t=0.15时的密度分布。可以看出，FDS -ZB -BVD格式在接触间断处比Roe格式的耗散更小，捕捉激波和稀疏波时与Roe格式具有相同的分辨率。

图3 Lax问题的密度分布

4.1.3 慢行激波问题

将计算区域[0,1]均匀划分成500个网格，初始条件为

(38)

该算例由一个孤立的右行慢激波构成。图4 展示了t=1.5时的密度分布。可以看出，Roe格式在波后出现了明显的振荡，而FDS -ZB -BVD格式有效地抑制了波后的振荡，表现出了更好的鲁棒性。

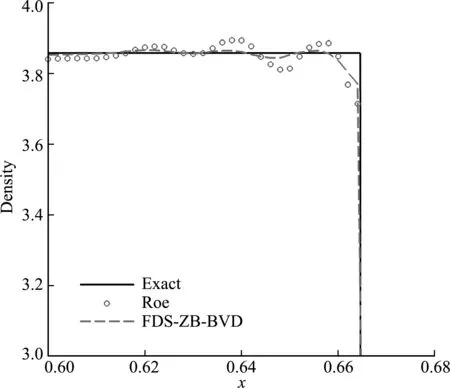
图4 慢行激波问题的密度分布

4.1.4 一维爆轰波问题

将计算区域[0,1]均匀划分成500个网格，初始条件为

(39)

该算例包含了复杂的间断结构和波系间的相互作用。图5展示了t=0.38时的密度分布。可以看出，FDS -ZB -BVD格式对于各个波系具有更高的分辨率。

4.1.5 激波-熵波相互作用问题

将计算区域[-5,5]均匀划分成1000个网格，初始条件为

(40)

该算例涉及到马赫数为3的激波和密度扰动产生的余弦波相互作用，产生了包含光滑和间断结构的流场。图6展示了t=1.8时的密度分布。可以看出，FDS -ZB -BVD格式比Roe格式具有更高的分辨率。

图6 激波-熵波相互作用问题的密度分布

4.2 二维算例

通过算例检验FDS -ZB -BVD格式在计算二维问题时的精度和鲁棒性。本文仅考虑用结构化四边形网格来划分规则的矩形区域，对于不规则的计算区域，可以使用非结构网格(如三角形网格)进行区域的划分，然后利用本文构造的数值格式结合旋转不变性式(5)计算界面的数值通量，最后应用有限体积方法来离散控制方程组。

4.2.1 二维黎曼问题

将计算区域[0,1]×[0,1]划分成512×512的正方形网格，初始条件为

(41)

图7展示了t=0.23时的密度等值线。可以看出，FDS -ZB -BVD格式比Roe格式具有更高的分辨率。该算例表明，本文构造的新型通量差分裂格式在计算二维问题时，可以有效地改善接触间断和相关流场结构的分辨率。

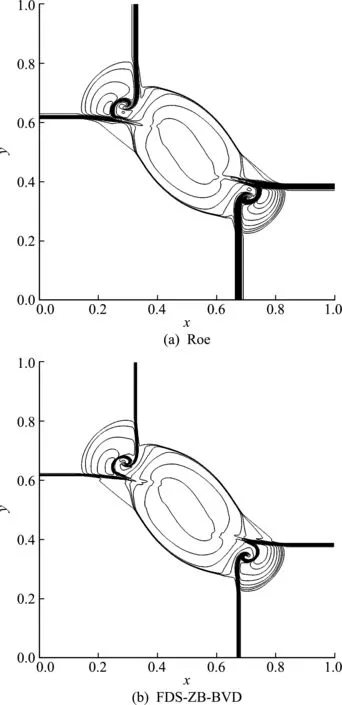
图7 二维黎曼问题的密度等值线

4.2.2 移动接触面问题

将计算区域[0,1]×[0,1]划分成200×200的正方形网格，初始条件为

(42)

该算例涉及到以(0.5,0.5)为圆心，0.3为半径的圆环接触面以速度(u,v)=(1,1)匀速运动。图8展示了t=0.15时的密度等值线，此时圆心的位置为(0.65,0.65)。可以看出，FDS -ZB -BVD格式大大改善了接触面的分辨率。

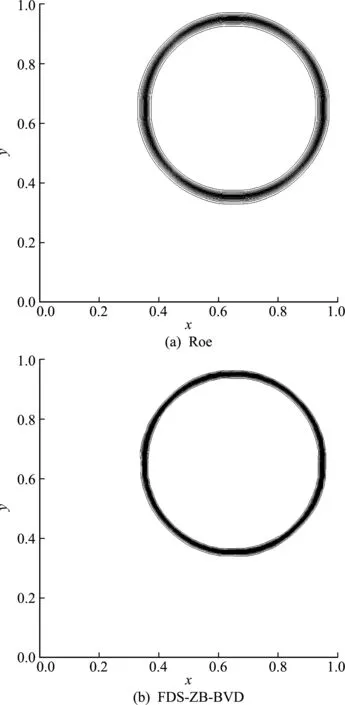
图8 移动接触面问题的密度等值线

4.2.3 Rayleigh-Taylor不稳定性问题

将计算区域[0,0.25]×[0,1]划分成120×480的正方形网格。区域上下部分两种流体的初始条件为

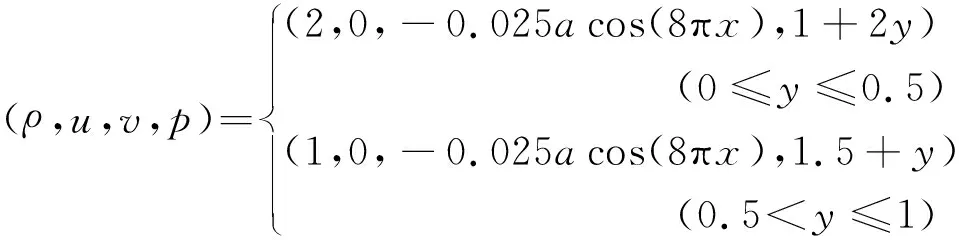
(43)

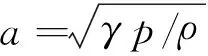
图9 Rayleigh-Taylor不稳定性问题的密度等值线

4.2.4 奇偶失联问题

能够精确捕捉接触间断的低耗散数值格式(如Roe和HLLC)在计算强激波问题时会遭遇红玉现象[11-14]。计算经典的奇偶失联问题来检验FDS -ZB -BVD格式的鲁棒性。初始时位于x=5处马赫数为10的平面激波沿x-方向传播。将计算区域[0,1500]×[0,20]划分成1500×20的均匀笛卡尔网格，除了y-方向的网格中心线处存在如下奇偶对称扰动,

(44)

激波右侧流体的密度为1.4，压力为1，两个方向的速度均为0。图10展示了t=120时的密度等值线。可以看出，Roe格式出现了明显的红玉现象，激波面完全破坏，而FDS -ZB -BVD格式有效地抑制了激波异常现象，得到了清晰和准确的激波面，表现出了更好的鲁棒性。

4.2.5 二维Sedov爆轰波问题

该问题涉及大压力比和强激波，常用来检验低耗散数值格式的鲁棒性。将计算区域[0,2.4]×[0,2.4]划分成480×480的正方形网格。初始时，区域中心高压区的压力为3.5×105，其余地方的压力为10-10，整个区域流体的密度为1，两个方向的速度均为0。图11展示了t=0.1时的压力等值线。可以看出，FDS -ZB -BVD格式消除了Roe格式非物理的红玉现象，表现出了更好的鲁棒性。

图10 奇偶失联问题的密度等值线

图11 二维Sedov爆轰波问题的压力等值线

5 结 论

基于Zha-Bilgen对流-压力通量分裂方法构造了一种新型的通量差分裂格式。由于压力子系统具有一组完备的线性无关的特征向量，因此构造传统的通量差分裂格式来进行计算。对于弱双曲的对流子系统，通过添加广义特征向量构造通量差分裂格式进行求解。为了提高接触间断的分辨率，利用界面变差下降(BVD)算法来减少对流通量耗散项中的密度差。激波稳定性分析表明新格式可以有效抑制数值误差的增长。一系列数值实验证明了本文构造的新型通量差分裂格式比传统的Roe格式具有更高的分辨率和更好的鲁棒性。因此，本文方法是一种精确和鲁棒的数值方法，可以广泛应用于可压缩流的数值模拟。