基于轴承座振动特性的大型同步调相机偏心故障程度诊断方法

李永刚， 贺鹏康， 马明晗， 岳文亭

(1. 华北电力大学 新能源电力系统国家重点实验室，河北 保定 071003；2. 国网甘肃省电力公司刘家峡水电厂，甘肃 永靖 731600)

近年来，随着高压直流输电的快速发展，大型同步调相机因具有响应速度快、无功补偿能力强等特点而得到广泛的应用[1-4]。因此，调相机自身的安全运行对提高电网动态电压稳定性、保证高压直流输电工程的电能质量高效率输送具有重要意义[5-7]。

同步调相机作为大型旋转设备，由于制造工艺、安装、运行、网侧故障冲击等原因，导致气隙之间分布不均匀，称作气隙偏心故障[8-10]。大量研究认为，当转子气隙偏心长度超过气隙总长度的10%时，则存在较严重的偏心故障。当调相机存在偏心故障时，会影响气隙磁场，从而加剧定转子与轴承座振动，严重时将会导致轴振超标[11-13]，对调相机安全运行与高压直流输电的稳定性产生影响。

对于气隙偏心故障，前人已有大量的研究。文献[14]较早地提出了气隙偏心的概念，并对气隙偏心的诊断、形成原因做了一定的研究。文献[15]通过分析发电机气隙偏心故障后的磁场与定子绕组环流特征，得出气隙偏心故障将会导致定子绕组基波环流增加，并提出利用环流特征来检测发电机的偏心故障。文献[16]提出了一种利用偏心故障后定子振动特性对发电机故障偏心程度进行识别的方法，但是由于试验的局限性，只对静偏心故障做了试验验证。文献[17]通过搭建发电机二维有限元模型，计算了动偏心故障后发电机定转子之间的不平衡电磁力，得出不平衡电磁力随着偏心故障程度的增大而增加的结论。目前，对于转子气隙偏心故障的研究对象多为大型汽轮发电机，并且研究主要集中在如何识别偏心故障，对于偏心故障程度的精确诊断方案提出较少。由于大型同步调相机并联在高压直流输电系统的送受两端，运行方式与大型发电机有较大的区别，机网的频繁交互容易对其产生冲击。同步调相机并网不久，对其气隙偏心故障研究较少，尤其是针对其精确的偏心程度诊断未见报道，并且对于现场运行调相机设置故障试验难度较大。因此对大型同步调相机的偏心故障程度的仿真分析与研究十分必要。

本文分析了动、静偏心故障后调相机轴承座振动特性，并利用轴承座二倍频振动与振动幅度对气隙偏心进行理论推导。通过有限元仿真验证了所提偏心故障程度诊断方案的正确性。本文主要改进在于，通过轴承座振动变化量对调相机动、静气隙偏心故障严重程度进行了原理分析与仿真验证，该鉴定方案为同步调相机的偏心故障程度的在线监测诊断具有极大的参考价值。

1 偏心故障前后轴承座振动特性

1.1 正常情况下轴承座振动特性

正常情况下，调相机气隙磁场分布均匀，气隙磁密可表示为

(1)

式中：f为气隙磁势；Λ为气隙磁导；F1为磁势幅值；αm为调相机的机械角；g为径向气隙长度。

正常情况下，轴承座所受单位面积电磁力为

(2)

将式(1)代入式(2)化简可得

(3)

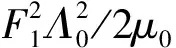
1.2 偏心故障下轴承座振动特性

如图1所示，调相机气隙偏心故障时，转子旋转中心发生偏移，与轴承座几何中心不再重合。

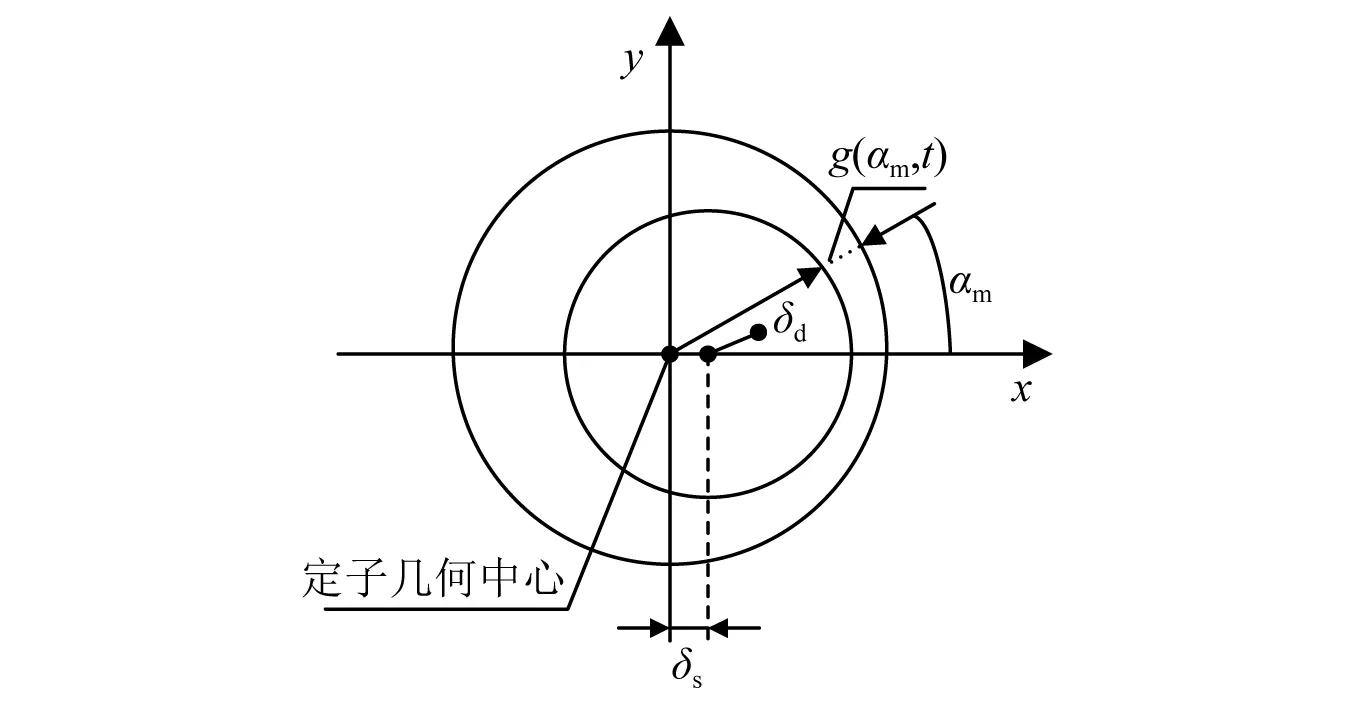
图1 调相机气隙偏心示意图Fig.1 Schematic diagram of static eccentricity

偏心故障下气隙表达式为

g(αm,t)=g0[1-δscosαm-δdcos(ωrt-αm)]

(4)

式中：g0为平均气隙；δs为相对静偏心值；αm为调相机的机械角；δd为相对动偏心值；ωr为机械角频率。对于同步调相机而言，ωr=ω(ω为电角频率)。

偏心故障后气隙磁密为

(5)

式中：Λ0为常值分量；Λs为静偏心引起的磁导分量，Λs=Λ0δs；Λd为动偏心引起的磁导分量，Λd=Λ0δd。

将式(5)代入式(2)可得轴承座单位面积所受电磁力为

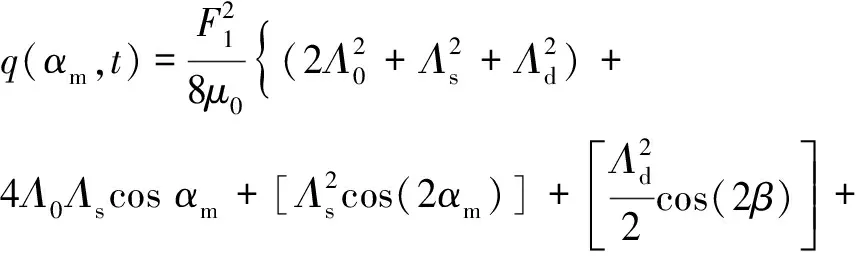
(6)

由式(6)可见，静偏心故障时(Λd=0，Λs≠0)调相机轴承座产生二倍频振动，动偏心故障时(Λd≠0，Λs=0)，调相机轴承座1倍、2倍、3倍、4倍频振动均会产生。

正常与偏心故障下对应各倍频频率成分的不平衡电磁力幅值，如表1所示。

表1 不同类型偏心故障下各倍频电磁力幅值Tab.1 Magnitude of magnetic pull force of each frequency multiplication under different types of eccentric faults

2 偏心故障程度鉴定方案

由于影响轴承座振动的因素很少，在调相机无缺陷情况下，轴承座的振动只与气隙不平衡电磁力有关。各频率成分振动幅值理论上与所受不平衡电磁力对应频率成分幅值成正比[18]。

由表1可知，偏心故障与正常情况下均使调相机轴承座产生二倍频振动，因此可利用二倍频振动幅值作为衡量偏心程度的一个指标。

根据前文推导可知，偏心故障后轴承座振动取决于气隙磁导的大小，因此偏心故障后气隙磁导与正常情况下气隙磁导的比值应等于偏心故障后轴承座振动幅度与正常情况下轴承座振动幅度的比值。

定义振动幅度计算公式为

s=max(si)

(7)

式中：si为第i个数据点的振幅值；s为振动幅度。由式(7)可知，振动幅度实际是不同状态下，轴承座振动的最大幅值，可反应在此状态下对轴承座的影响程度。

2.1 静偏心故障鉴定方案

静偏心故障后轴承座二倍频振动幅值与正常运行时轴承座二倍频振动幅值比值关系为

(8)

根据式(8)可得二倍频故障严重程度可表示为

(9)

静偏心故障后轴承座实测振动幅度与正常运行时的振动幅度比值关系为

(10)

根据式(10)可得振动烈度故障严重程度可表示为

λj2=yj/yz-1

(11)

将上述两种计算方法的故障严重程度取平均值可得

(12)

式中：d2j为轴承座二倍频实际测量值；d2z为正常运行的二倍频振动幅值；λj1为二倍频振动引起的静偏心故障程度；yj为轴承座实际振动幅度；yz为正常运行时轴承座振动幅度；λj2为振动烈度引起的静偏心故障程度；λj为静偏心故障程度。

2.2 动偏心故障鉴定方案

动偏心故障后轴承座二倍频振动幅值与正常运行时轴承座二倍频振动幅值比值关系为

(13)

根据式(13)可得二倍频故障严重程度可表示为

(14)

动偏心故障后轴承座实测振动幅度与正常运行时的振动幅度比值关系为

(15)

根据式(15)可得振动幅度故障严重程度可表示为

λd2=yd/yz-1

(16)

将上述两种计算方法的故障严重程度取平均值可得

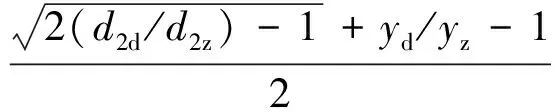
(17)

式中：d2d为轴承座二倍频实际测量值；λd1为二倍频振动引起的动偏心故障程度；yd为轴承座实际振动幅度；λd2为振动幅度引起的动偏心故障程度；λd为动偏心故障程度。

3 仿真验证

3.1 调相机基本参数

本文以某换流站一台TTS-300-2型双水内冷调相机为研究对象，其主要参数如表2所示。

表2 调相机的基本参数Tab.2 Adjust the basic parameters of the camera

3.2 调相机场路耦合仿真模型

如图2所示，为了计算调相机偏心故障后不平衡电磁力，本文采用Maxwell搭建了调相机二维有限元物理模型，在此模型当中可设置转子偏心故障，本文设置最小气隙处为调相机最右侧。图3为调相机外电路，定子绕组施加三相电压源激励，励磁绕组施加直流源激励，当设置不同程度偏心故障时外电路不需要更改。

图2 调相机二维有限元模型Fig.2 The finite element physical model of the SC

图3 外电路Fig.3 External circuit

网格剖分后的每个网格单元都满足式(18)所示的调相机二维磁场数学模型。

(18)

式中：AZ为矢量磁位；μ为磁导率；JZ为Z轴电流密度分量；AZ0为边界T的已知值，符合第一类边界条件。

3.3 不平衡电磁力仿真结果

大量文献研究表明，不平衡电磁力是影响机组振动的主要因素[19]。本文采用Maxwell应力张量法计算了正常情况、不同程度静偏心、不同程度动偏心故障下轴承座所受不平衡电磁力，结果如图4所示。

图4 不同程度偏心故障下轴承座所受不平衡电磁力Fig.4 Unbalanced magnetic tension on the stator under different degrees of eccentricity faults

由图4可见，气隙正常时轴承座所受不平衡电磁力较小；当气隙发生偏心故障时，无论静偏心还是动偏心，随着偏心程度的增大，轴承座所受不平衡电磁力的幅值也越大。动、静偏心14 mm时轴承座所受不平衡电磁力的最大值均超过了300 kN。

不同类型偏心故障时轴承座所受不平衡电磁力的谐波分析，如图5所示。其中，静偏心故障时二倍频幅值随着故障程度的加深而增大，动偏心故障时各个倍频幅值随着故障程度的加深均增大，这与前文理论推导结果一致。对应的二倍频幅值与振动幅度数值，如表3所示。由于本文进行故障诊断只用轴承座二倍频振动，表3只给出二倍频电磁力幅值。

图5 不同程度偏心转子所受电磁力的谐波分析Fig.5 Harmonic analysis of electromagnetic force on rotors with different degrees of eccentricity

表3 偏心故障前后轴承座所受二倍频电磁力与振动幅度Tab.3 Double-frequency electromagnetic force and vibration amplitude suffered by the bearing seat before and after the eccentric fault

3.4 偏心故障程度诊断结果

将表3中所列出的不同程度的偏心故障的二倍频电磁力幅值与振动幅度采用式(8)～式(17)计算所得调相机偏心故障程度诊断结果与实际运行状态对比，如表4所示，结果所示的静偏心诊断误差最高为4.5%、动偏心诊断误差最高为10.8%，可见诊断结果较准确。

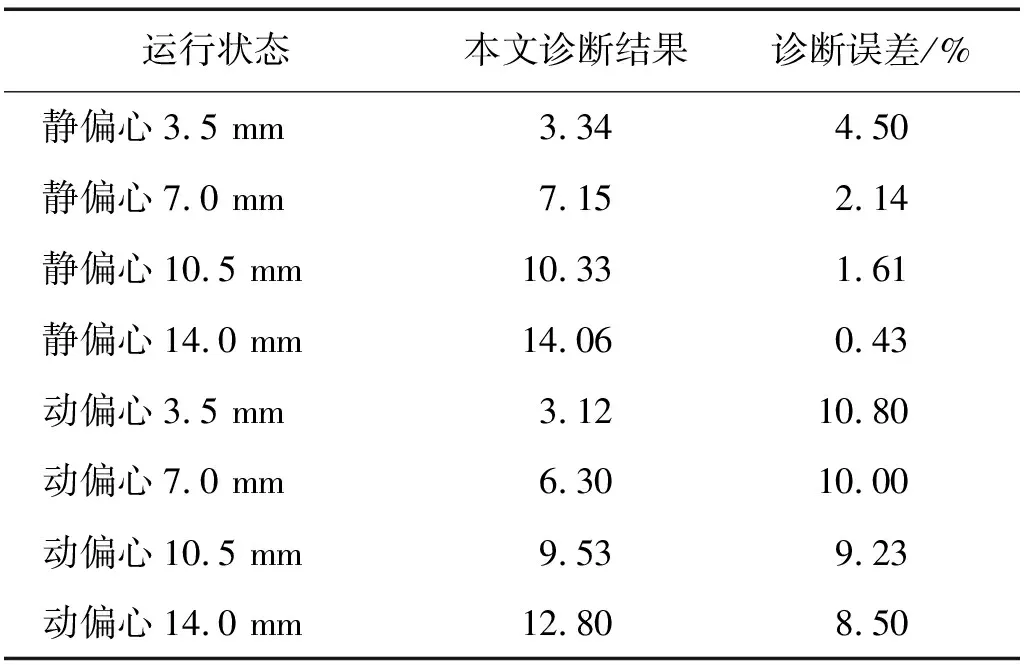
表4 本文所提方法诊断结果与实际偏心程度对比Tab.4 Comparison of calculation results of the method proposed in this paper and actual degree of eccentricity

如图6所示，本文所提故障程度判断方法较实际故障程度误差较小，并且静偏心故障程度诊断结果较动偏心更接近于实际值。

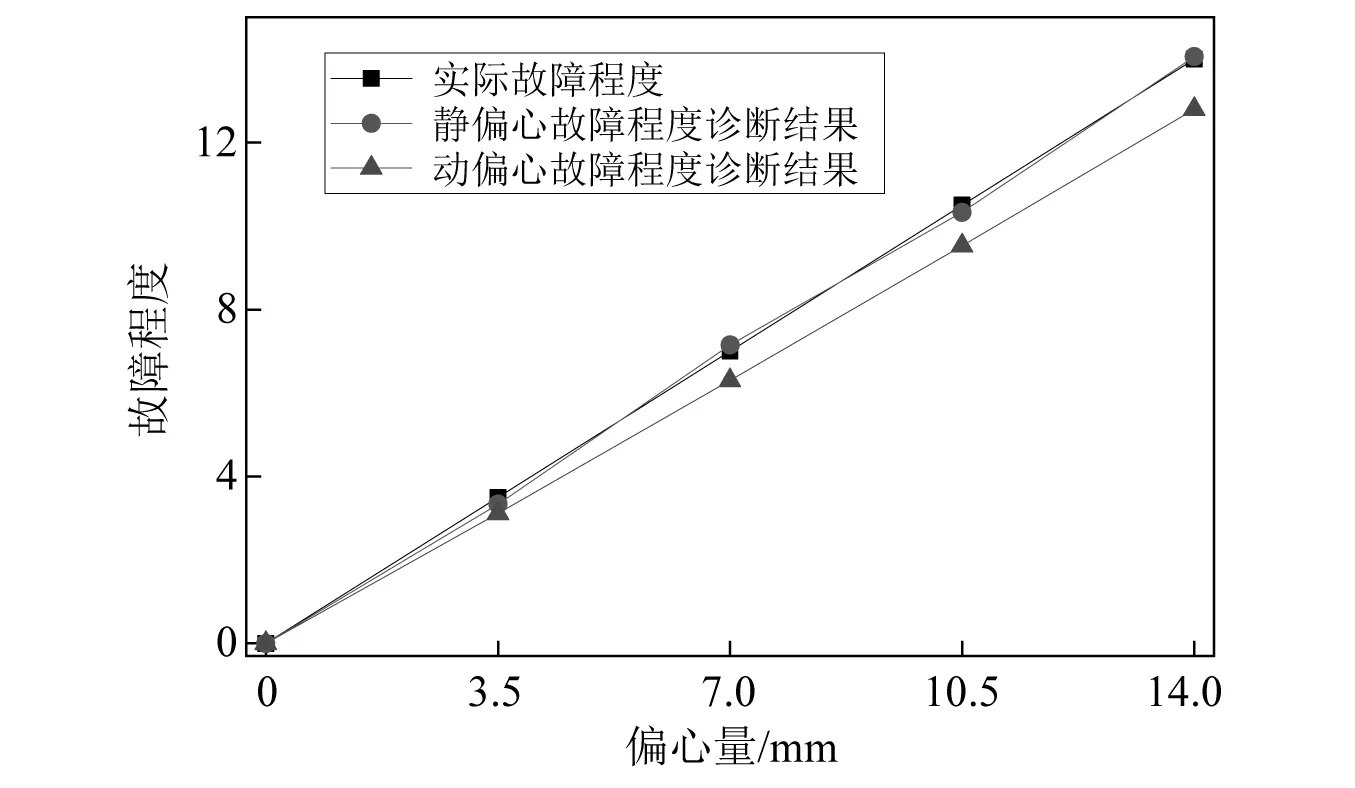
图6 本文方法与实际故障程度对比曲线Fig.6 Comparison curve between the method in this paper and the actual failure degree

从图7所示的不同故障程度诊断误差曲线当中可以看出，偏心故障程度越大，本文所提故障诊断方案的诊断结果误差越小，越接近实际值。在静偏心14 mm时，诊断误差值为0.43%。

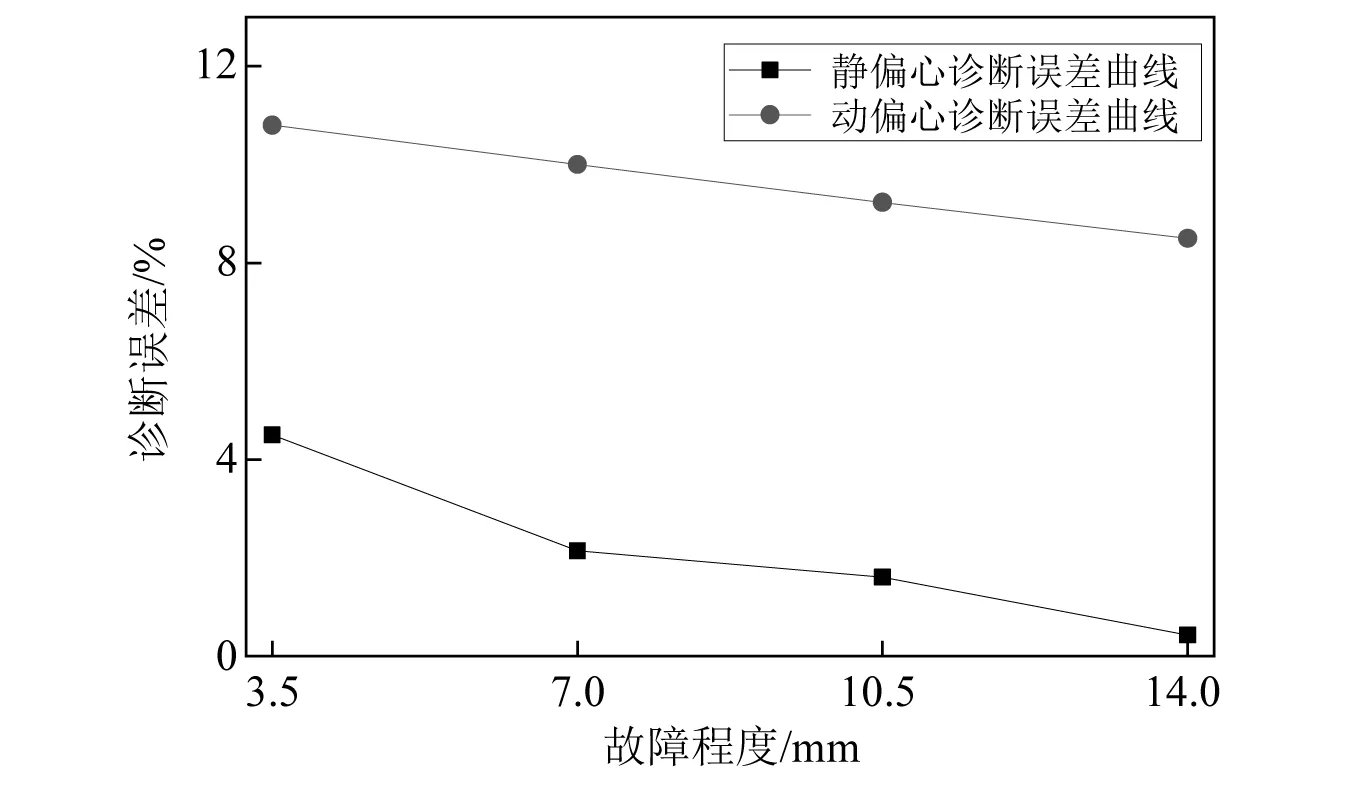
图7 不同故障程度诊断误差曲线Fig.7 Diagnosis error curve of different fault levels

4 可行性分析

由于300 Mvar大型同步调相机挂网运行时间尚短，缺乏现场的实际故障数据，且对大型调相机设置偏心故障试验是不可行的。因此，本文基于Maxwell构建了场-路耦合仿真模型计算了偏心故障前后调相机的振动特性，实现了提取故障特征数据的目的。实际上，在调相机出厂时已安装位移传感器[20]用来监测轴承振幅。某300 Mvar调相机轴承座振动测点布置图，如图8所示，在轴承座水平方向和垂直方向均安装CYQ-9250型位移传感器，用来检测轴承振动数据。由于位移传感器安装方便、成本低，因此该方法可以在现场得到具体验证和应用。

图8 轴承座振动测点布置Fig.8 Vibration measuring point arrangement of bearing seat

5 结 论

本文针对于大型同步调相机提出了一种利用轴承座振动特性判定调相机转子偏心故障程度的方案，并利用有限元仿真进行了验证，得出以下结论：

(1) 正常情况下调相机轴承座只存在二倍频振动，静偏心故障导致二倍频振动幅值增大，动偏心故障导致各个倍频振动幅值均增大，并且振动幅值随着偏心故障程度的增加而增加。

(2) 利用振动幅度与二倍频振动诊断结果的均值计算方法能够客观的鉴别出偏心故障程度，提高鉴别精度，并且偏心故障程度越大，该方案的鉴别精度越高，鉴别误差越小。当偏心为14 mm时，静偏心故障的诊断结果误差为0.43%，动偏心故障的诊断结果误差为8.5%。

(3) 利用该鉴定方案的静偏心故障程度诊断误差整体低于动偏心故障程度诊断误差。

本文所提大型调相机偏心故障程度在线诊断方法具有诊断精度高、方法简单等优点。通过对转子偏心故障程度的诊断，以及同时采取相应的应对措施能够将故障带来的危害控制在最小的同时也对调相机的安全稳定运行有着很大的积极意义。