基于改进低秩稀疏正则化的CFRP电阻抗层析成像算法研究

马 敏， 于 洁， 范文茹

(中国民航大学 电子信息与自动化学院, 天津 300300)

碳纤维复合材料作为一种新型复合材料，具有高比强度、高比模量及稳定性好等优点，已被广泛应用于航空航天领域[1-2]。碳纤维复合材料结构复杂，由于其导电性存在各向异性的特点[3]，常用的铺设方式有[0°/90°]和[0°/45°/90°]。碳纤维复合材料在生产制造和使用过程中可能造成结构损伤，损伤可能出现在材料的表面或者内部，一旦出现损伤对于工业应用来讲可能是致命的[4]。因此，对碳纤维复合材料进行有效的损伤检测十分必要。随着碳纤维复合材料的广泛使用已经出现了很多检测方法。其中，电阻抗层析成像技术以其无创性、可视化、无辐射、操作简单、成本低等优点已被广泛研究应用[5]。电阻抗层析成像(electrical impedance tomography，EIT)检测通过在被测区域周围施加电流激励获取测量电压信号，计算电导率分布情况，进而反演出被测区域图像[6]。但是，EIT逆问题求解具有病态性和不适定性，重建算法的好坏一定程度上决定了图像重建质量。常用的逆问题的求解算法包括线性投影法[7]、Tikhonov正则化算法[8]和Landweber算法[9]等。它们适用于简单损伤的检测，但在复杂损伤检测中会出现严重的电极伪影且其重建时间一般较长。

为了有效提高重建质量，改进重建算法是相当重要的。基于L2范数作为凸优化的算法因其计算简单、求解稳定被广泛采用，但其过于平滑没有产生更多稀疏的解，使图像分辨能力较差[10]。而L0范数可以克服L2范数正则化的缺点，增强成像目标的稀疏性，但L0范数的求解属于NP-hard问题[11]。在求解EIT逆问题时，采用L0范数的替代模型近似求解稀疏重建算法受到广泛应用[12-13]。Lp伪范数模型[14]通过增加一个自由度可以更好地逼近真实解L0，增强解的稀疏性的同时，也可以更好地呈现图像的局部信息，提高算法地抗噪声能力。此外，近年来，低秩矩阵约束在图像重建领域也受到了广泛关注与应用。核范数[15]一直被用于解决低秩问题。由于EIT重建图像呈现出低秩特征，若有效利用先验信息用于图像重建过程将有益于提高重建精度[16]。

目标函数一旦构建，选择合适的求解器进行求解也格外重要。分裂布雷格曼方法[17-18]已被广泛应用于求解L1范数的凸优化问题，它将目标函数分裂成几个子问题进行求解，在取得良好的重建效果的同时，进而缩短重建时间。

综上，本文提出的改进低秩稀疏正则化算法主要进行了三点优化：

(1)引入Lp伪范数模型，获得更逼近L0范数模型稀疏解，有效提高图像重建质量同时增强算法的鲁棒性；

(2)引入核范数作为低秩约束项，有效利用图像重建过程中的先验信息以提高图像重建的分辨率；

(3)利用分裂布雷格曼方法对泛函进行求解，增强算法的实时性。

1 CFRP损伤基于EIT重建原理及传统算法

1.1 CFRP层压板电学性质

CFRP复合材料是由导电碳纤维和绝缘树脂聚合物复合而成。由于碳纤维是导电材料，并且碳纤维的纤维方向的电导率较高，纤维方向的垂直方向和层压板的厚度方向的电导率较低，以致CFRP的导电性具有各向异性的特点。因此，CFRP层压板通常被简化为多层叠加的均质连续各向异性材料[19]，电导率张量Σ为

(1)

式中：σ11为纤维方向电导率；σ22为纤维方向的垂直方向电导率；σ33为材料板厚度方向的电导率。

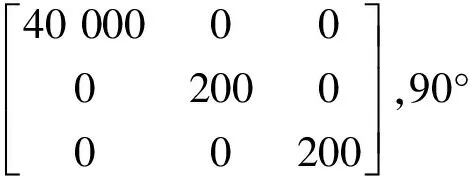
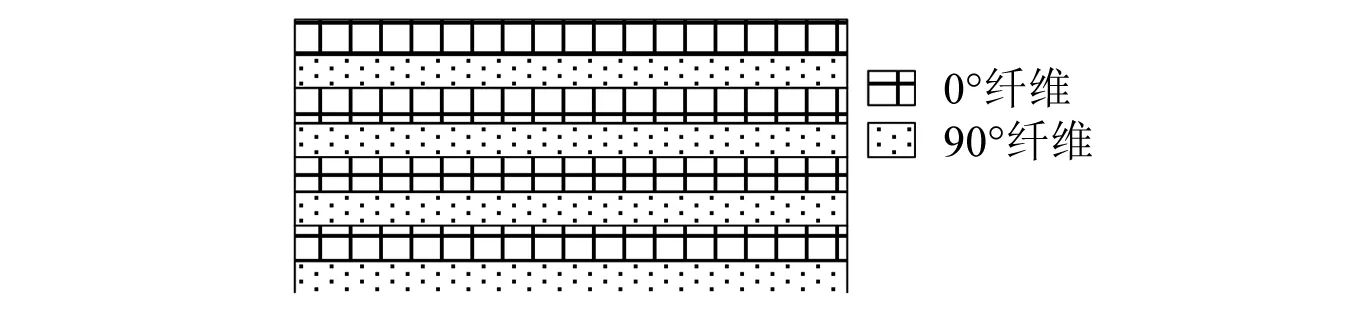
图1 CFRP 层压板模型Fig.1 The model of CFRP

1.2 EIT图像重建原理

EIT图像重建是通过激励电流I和边界测量电压V反演场域内部电导率σ的分布情况[20]。 EIT图像重建过程如图2所示。

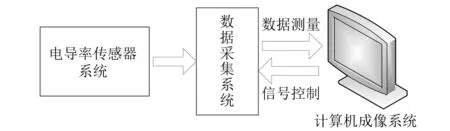
图2 EIT图像重建过程Fig.2 EIT image reconstruction process

电导率分布通过建模和有限元离散化对应的动态EIT测量值可表示为

V=U(σ;I)=R(σ)I

(2)

式中：U(·)为σ和I～V映射的正演模型；R(σ)为σ到电阻的映射模型。

在电导率σ变化很小的情况下，通过线性化方程组的方法可以来精确地求解EIT逆问题。

δU=U′(σ0)=Jδσ

(3)

式中： δU∈Rm×1(m为独立电压测量值个数)为材料损伤前后电压测量差值；δσ∈Rn×1(n为重建图像中的像素数)为电导率张量模值变化量的分布矩阵；J∈Rm×n为Jacobian矩阵。

1.3 EIT传统算法

1.3.1 Tikhonov正则化算法

Tikhonov正则化算法根据最小二乘法和平滑准则将EIT的不适定逆问题转化为一个优化问题。

(4)

式中：L为正则化算子，通常选为单位矩阵I；λ为正则化系数。

由此，可获得Tikhonov正则化算法的解为

x=(JδTJδ+λI)-1JδTδU

(5)

1.3.2 稀疏正则化算法

为了增强解的稀疏性，L1范数作为解的惩罚项被广泛应用于EIT图像重建。

(6)

传统L1算法是应用稀疏正则化(SpaRSA)方法[21]求解式(6)得出如下解估计值序列

(7)

(8)

式中，α为迭代步长，采用自适应谱分析法[22]更新。

根据split Bregman方法求解式(6)，可得如下迭代方案

(9)

2 改进低秩稀疏正则化算法

受电极数量、位置和“软场”效应的影响，EIT逆问题求解是一个欠定、病态问题。正则化方法是处理不适定问题的一个常用方法，它通常由两个部分组成，即解的精确测度和稳定泛函，即惩罚项。目前，L1范数作为惩罚项来刻画解的稀疏性被广泛应用，但L1正则化与真实的稀疏解仍有很大差距，在复杂损伤模型中，难以取得令人满意的成像结果。

近年来，低秩正则化在图像重建领域受到了广泛关注，通过利用成像目标数据结构中的低秩特性以提高重建质量。但是，当仅考虑低秩特征时，重建结果仍欠佳。因此，本文采用低秩正则化和稀疏正则化的有效结合方式，以提高重建质量。首先引入Lp伪范数，通过增加一个自由度来增强重构目标解的稀疏性，更好的刻画图像的局部信息，其次，引入核范数作为低秩正则化项，通过描述重建对象的多个特征的先验信息来提高重建精度，最后，引入分裂布雷格曼方法对新的目标泛函进行求解，通过将目标泛函分裂成多个子问题来提高成像质量和缩短成像时间。

利用分裂布雷格曼方法求解稀疏正则化问题的EIT重建过程可被描述为

s.t.d1=δσ,d2=X

(10)

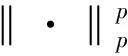
式(4)可依据分裂布雷格曼方法分裂成如下几个简单问题

(11)

(12)

(13)

分裂布雷格曼算法的好坏主要取决于分裂出来的几个子问题的求解算法的优劣。对于以上三个子问题，采用简单的梯度下降法求解式(11)，式(12)是标准核范数最小化问题，应用奇异值阈值迭代方法进行求解，根据Lp伪范数收缩算子来更新式(13)。

(14)

(15)

(16)

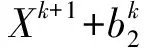
表1 改进低秩稀疏正则化算法

3 试验验证

仿真使用COMSOL5.4软件建立八层各向异性 CFRP 层压板模型，根据CFRP材料的常见损伤，构建三类损伤类型模型：冲击损伤模型、分层损伤模型、裂纹损伤模型。所构建的损伤模型如图3所示。模型a是一个单冲击损伤，损伤为一个半径为5 mm、高度为3.2 mm的圆柱体，位于层压板中心；模型b是一个三冲击损伤，三个损伤均为半径为5 mm、高度为3.2 mm的圆柱体；模型c是一个单分层损伤，损伤为一个半径为5 mm，高度为0.8 mm的圆柱体，位于层压板中心；模型d是一个双分层损伤，左侧损伤为一个半径为8 mm，高1.2 mm的圆柱体，右侧损伤为一个半径为6 mm，高1.2 mm的圆柱体；模型e为一个裂纹损伤，损伤是一个长35 mm，宽1 mm，高3.3 mm的长方体，位于板材中心斜左45°的位置。

图3 层压板损伤模型(mm)Fig.3 The models of CFRP laminates(mm)

每个电极为一个半径1.5 mm，高10 mm的铜质圆柱，嵌入在CFRP层压板四周，电流激励大小为4 500 A/m2。

选取Tikhonov正则化算法、L1正则化算法、分裂布雷格曼算法和改进低秩稀疏正则化算法分别对损伤图像重建并进行对比分析。根据对不同算法的成像效果以及评价指标进行比较分析。评价指标为图像的相关系数(correlation coefficient， CC)[23-24]和损伤面积误差估计Serror[25]。CC值越接近于1，表示重建图像与真实图像的误差越小，相关程度越大，重建质量越高。损伤面积误差估计采用Canny算子和最小二乘椭圆拟合出重建图像的损伤面积大小与真实模型损伤面积大小相比较得出，以更好比较说明重建损伤和真实损伤大小的相似程度。

(17)

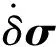
(18)

式中：S′为图像重建损伤面积大小；S为真实损伤面积大小。

3.1 无噪声仿真试验

对理想测量状态进行仿真，可验证算法在求解EIT逆问题中的有效性。此时，EIT系统所获取的电压测量值中不含噪声。CFRP材料损伤重建效果对比如图4所示， CFRP材料损伤重建相关系数对比如图5所示。CFRP材料损伤面积误差估计对比如表2所示。

图4 无噪声下不同算法CFRP材料损伤重建图像对比Fig.4 Comparison of damage reconstruction images of CFRP with different algorithms without noise

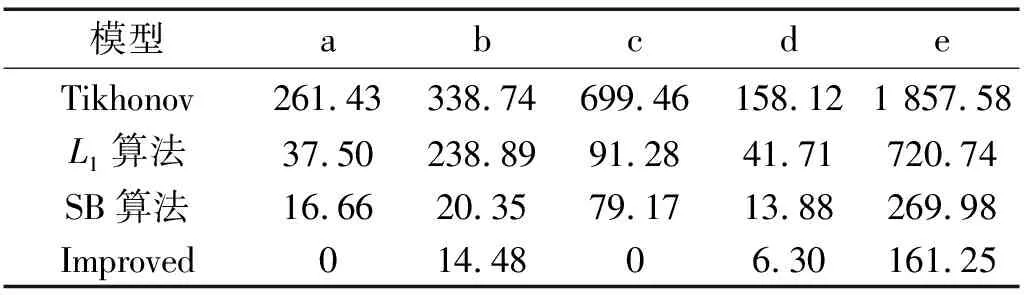
表2 CFRP材料损伤面积误差估计对比

由图4可知，Tikhonov算法能基本确定并显示出损伤的大体位置，但不能准确还原损伤的位置和大小，重建图像边缘受电极的影响严重，所成伪影发生严重粘连现象。L1正则化算法所成图像能较清楚地显示损伤的具体位置但不能准确反映其大小，伪影得到了明显改善，但在三冲击损伤、双分层损伤中存在严重的电极伪影，分裂布雷格曼算法比Tikhonov算法、L1正则化算法更有效地减弱了电极的影响，而且能够准确还原损伤的位置和大小，但仍存在所成损伤轮廓不清晰、图像边缘电极伪影严重的现象，而改进低秩稀疏正则化算法的重建图像在形状、大小及位置方面最接近真实损伤，所成损伤轮廓清晰，重建图像边缘电极伪影明显减少，在双分层损伤模型中，真实反映了不同大小的两处损伤，优势明显。

由图5可知，改进低秩稀疏正则化算法与Tikhonov正则化算法、L1正则化算法和分裂布雷格曼算法相比，图像相关系数的显著提高，所成图像精度更高。在模型a中，改进算法相关系数达0.929 7，也进一步验证了低秩稀疏正则化算法在CFRP复合材料检测中具有良好的应用前景。

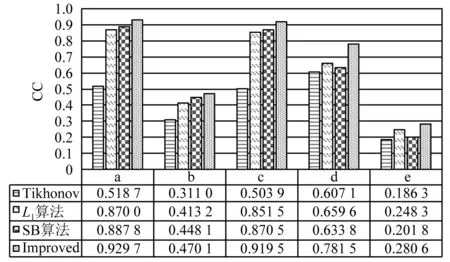
图5 图像相关系数对比Fig.5 Comparison of image correlation coefficient

从表2中可以看出，Tikhonov正则化算法损伤面积误差估计最大，所成损伤面积均是大于真实损伤面积，在裂纹损伤中高达1 857.58%。而L1正则化算法最能在单冲击模型中反映真实损伤面积大小；在单分层中，虽取得了较好的成像效果和较高的相关系数，但是由于电极伪影影响，它的面积误差估计值达到91.28%。 分裂布雷格曼算法的损伤面积误差估计值较Tikhonov正则化算法、L1正则化算法明显减少，但在单分层损伤中也出现了较高的面积误差。而改进低秩稀疏正则化算法所成损伤大小与真实损伤最为相近，均取得了较低的面积误差估计值，特别地，在单冲击损伤和单分层损伤中面积误差可忽略不计。

通过以上比较分析可以得出，改进低秩稀疏EIT算法有效削弱了电极影响，更好反映图像边缘信息，提高了重建图像质量，所成损伤更贴近真实分布情况，具备适用性和应用前景。

3.2 噪声仿真试验

在实际工业测量中，测量数据不可避免地存在随机干扰，即测量噪声。它会增加逆问题的不适定性，使成像结果受到影响。图像重建算法是否具有良好的鲁棒性来减弱噪声的影响也是一项重要的评价指标。比较5%和10%噪声对最终重建结果的影响，分析改进低秩稀疏正则化算法的鲁棒性。5%和10%噪声试验图像重建结果与相关系数对比分别如图6和图7所示。

由图6、图7可知，在5%噪声、10%噪声的干扰下，改进低秩稀疏正则化算法仍能准确反映损伤位置和大小，更好地呈现图像边缘信息，电极影响较小，与无噪声情况下的损伤图像相近。而L1算法、分裂布雷格曼算法在噪声的干扰下所成损伤均发生了不同程度的畸变，所成损伤图像模糊，电极伪影影响严重。此外，在噪声干扰下，改进低秩稀疏正则化算法所成图像仍能保持较高的相关系数。

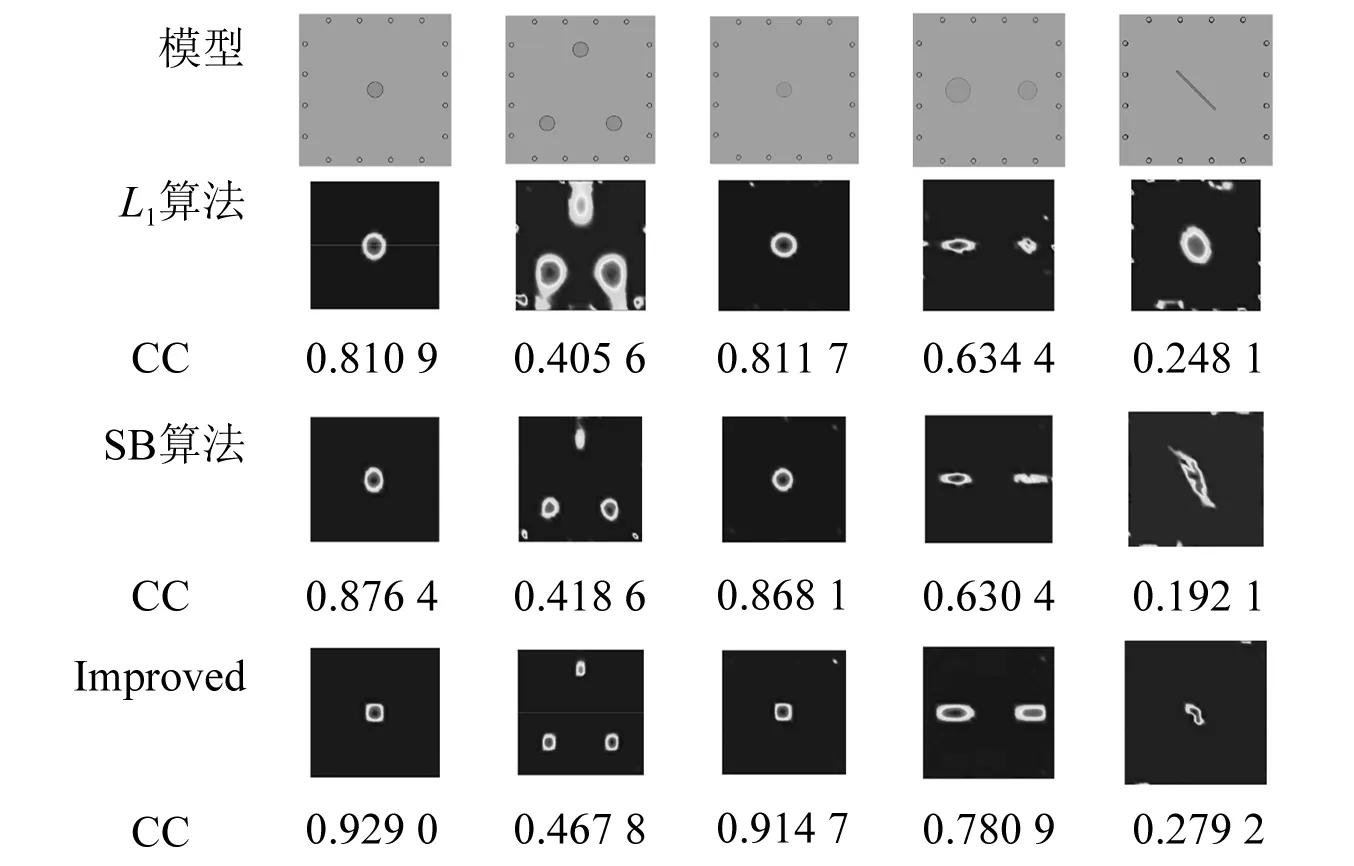
图6 5%噪声试验图像重建结果与相关系数对比Fig.6 Comparison of image reconstruction results and correlation coefficient with 5% noise experimental

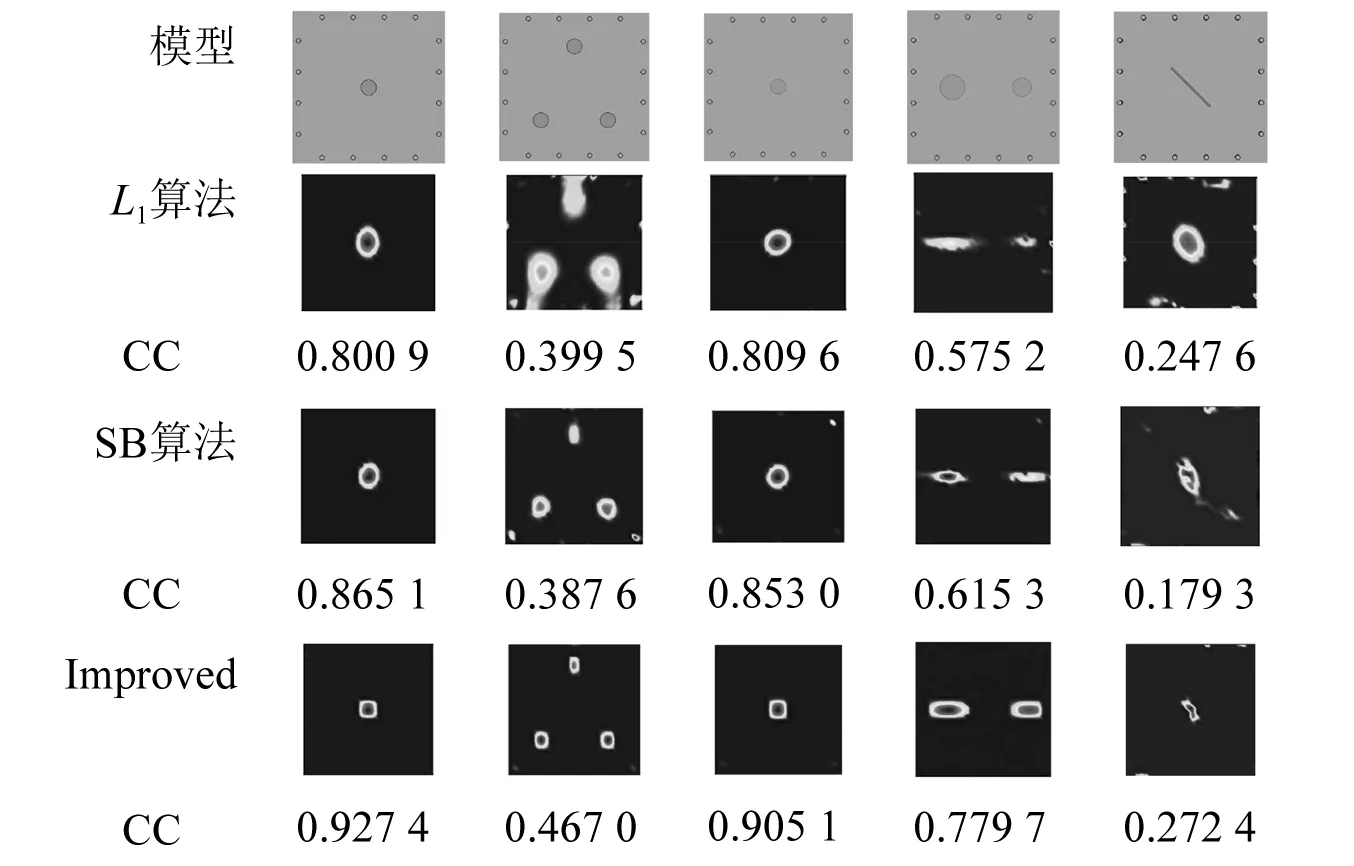
图7 10%噪声试验图像重建结果与相关系数对比Fig.7 Comparison of image reconstruction results and correlation coefficient with 10% noise experimental

由图8可以看出，改进低秩稀疏正则化算法与无噪声情况下的相关系数相近，进一步验证了改进低秩稀疏正则化算法能够有效弱化噪声影响，具有良好的鲁棒性。

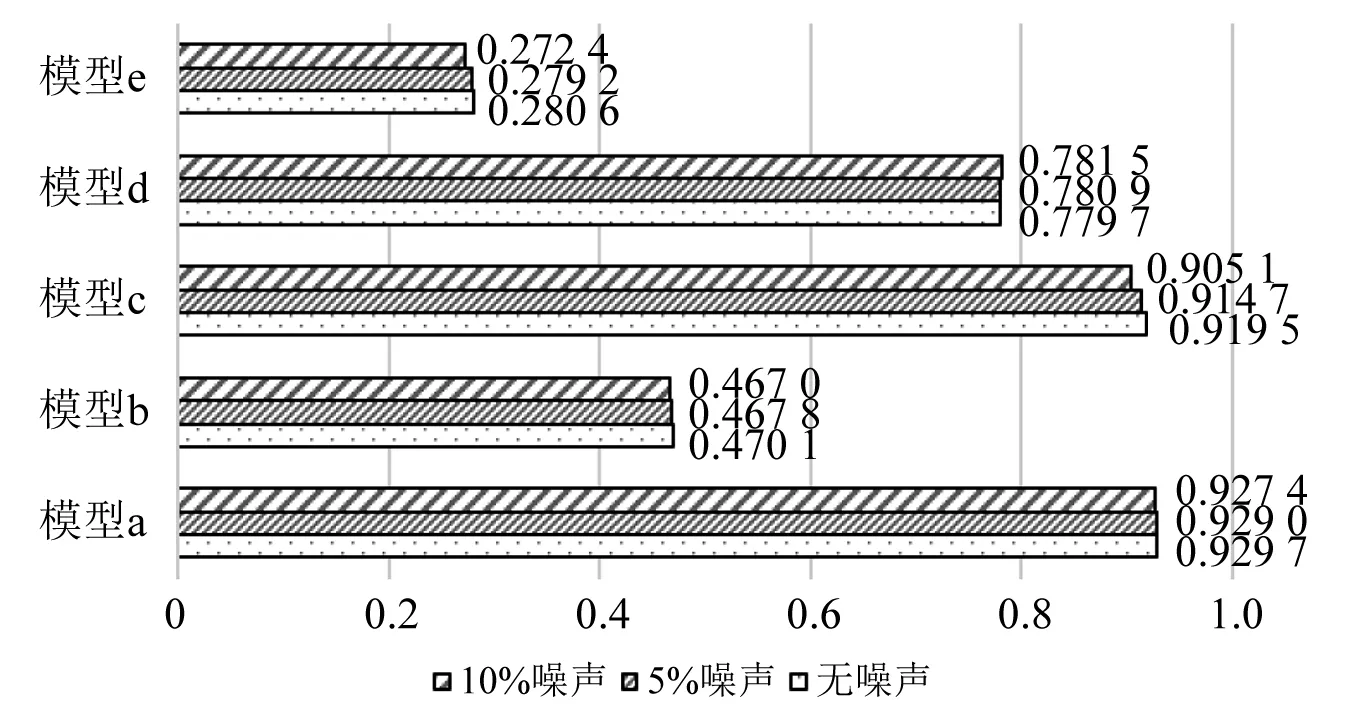
图8 不同噪声下改进算法相关系数对比Fig.8 Comparison of correlation coefficients of the improved algorithm under different noises

由表3可知，在不同噪声干扰下，改进低秩稀疏正则化算法重建损伤的面积误差估计值均相近，对于单冲击和单分层损伤模型，面积误差估计值仍为0%，所成损伤大小与真实损伤大小十分相近，进一步验证了该算法良好的鲁棒性和适用性。

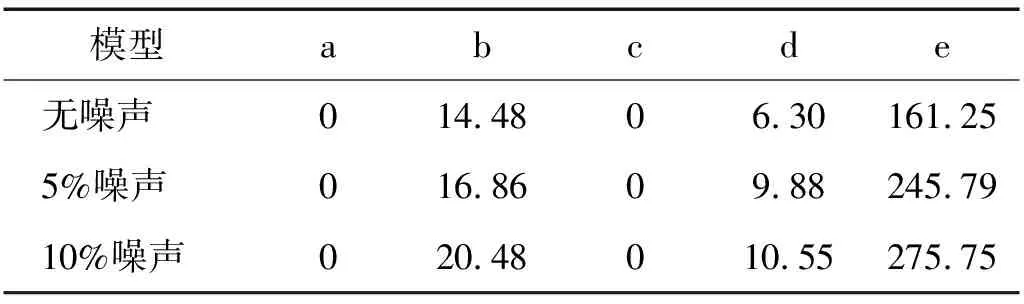
表3 不同噪声下改进算法损伤面积误差估计对比

3.3 系统试验

CFRP复合材料EIT损伤检测试验平台如图9所示。CFRP板材长10 cm，宽 10 cm，高0.32 cm， 将16个电极均匀放置在板材四周，电极连接电流注入和电压测量的多路复用器，以实现对电极的循环激励和循环测量。电流激励由精密电流源(KEITHLEY 6221)提供，给相邻电极施加的激励电流大小为100 mA，使用多功能开关测量单元( KEYSIGHT 34980A)和电枢矩阵开(KEYSIGHT 34932) 采集测量数据，由基于LabVIEW使用系统软件进行开关量的切换。最后，通过接线端子模块(KEYSIGHT 34932T) 将采集到的电位数据导入图像处理程序以得到图像重建结果。

试验所用CFRP层压板大小为100 mm×100 mm，四周镶嵌16个铜质铆钉，每一边四个铆钉，间距为20 mm，铆钉中心到CFRP板材边界距离为5 mm，成像区域为80 mm×80 mm。

试验模拟了三种冲击损伤和一种裂纹损伤。其中，单冲击模型和上下双冲击模型损伤孔半径均为3 mm，斜对角双冲击模型损伤孔半径为5 mm，裂纹模型损伤大小为1 mm×40 mm×1 mm，成像效果如图10所示。

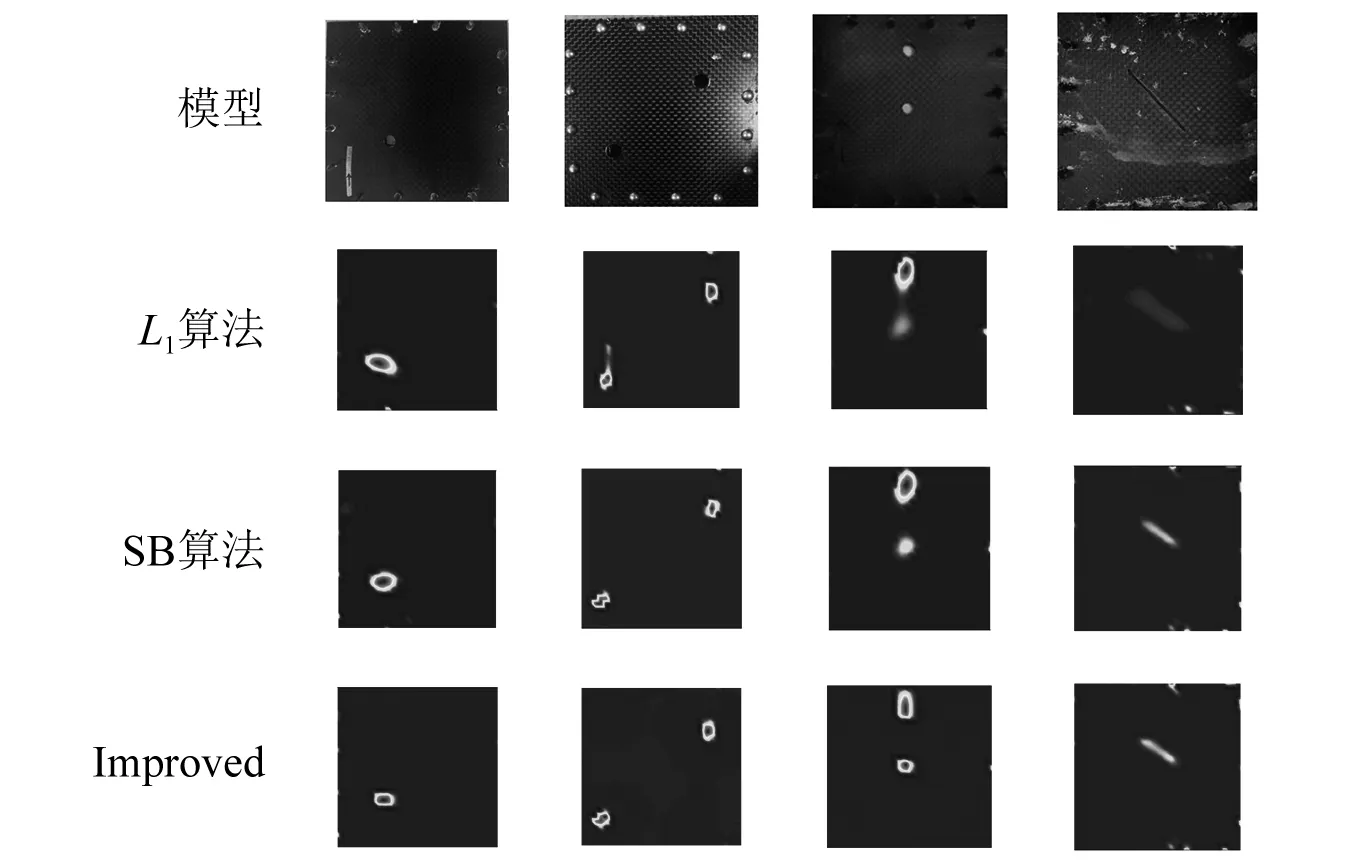
图10 CFRP复合材料检测试验成像效果对比Fig.10 Comparison of imaging results of CFRP composite material detection experiments

由图10可知，L1正则化算法对于单冲击损伤不能较好的反应损伤大小，对于双冲击损伤出现模糊不清现象，裂纹损伤的成像对比度较低，并且出现了电极伪影。分裂布雷格曼算法较L1正则化算法的成像质量有所提高，但损伤仍不够清晰、边缘电极伪影严重，且出现了损伤畸变现象。而改进低秩稀疏正则化算法重建图像电极伪影得到了改善，损伤轮廓清晰明了，能够更准确的反映损伤的大小和形状，对于裂纹损伤也更加清晰明显。试验结果证明，改进低秩稀疏正则化算法具备实用性，为EIT系统应用于CFRP复合材料实际检测提供依据。

4 结 论

本文通过仿真试验反演出的图像及评价指标验证了改进低秩稀疏正则化算法对CFRP材料损伤检测的有效性。

改进低秩稀疏正则化算法重建图像质量能够增强解的稀疏性，改善EIT逆问题的病态性，对于冲击损伤、分层损伤和裂纹损伤均具有良好的反演能力，成像质量均优于传统的Tikhonov算法、L1正则化算法和分裂布雷格曼算法，且成像效果稳定，具有良好抗干扰性，具备CFRP复合材料损伤检测的良好应用前景。