一个(2+1)-维推广KdV6方程的李对称分析
苏 丹
(1.湛江幼儿师范专科学校,广东 湛江 524084;2.岭南师范学院基础教育学院,广东 湛江 524037)
0 引言
作为KdV6方程的一种高维推广,WAZWAZ[1]首次提出了如下形式的(2+1)-维推广KdV6方程:
(1)
基于广田双线性方法给出了该方程的多孤立子解和多奇性解.GORDOA[2]对该方程进行了可积性测试,指出该方程不能通过潘勒韦检验.本文将尝试利用基于无穷小变换的李对称方法对方程(1)的求解问题进行研究.李对称方法由挪威数学家SOPHUS LIE于1870年左右提出[3-4].该方法不需要特别的变换技巧,通过寻找保持方程形式不变的对称群简化原来的方程并获得精确解,不仅适用于线性微分方程,也适用于非线性微分方程,是微分方程研究领域强有力的解析工具之一.
本文将利用李对称方法研究方程(1)的对称约化及精确解.
1 方程(1)的李对称分析
考虑方程(1)的单参数李对称群的无穷小变换:
(2)
其中,ε是单参数,其对应的李代数生成元是
X=ξ(x,y,t,u)∂x+η(x,y,t,u)∂y+τ(x,y,t,u)∂t+ω(x,y,t,u)∂u.
(3)
基于文献[5-8]中的算法,将X的7次延拓作用到方程(1)后为0可以得到对称性决定方程组,利用符号计算软件求解决定方程组得到
(4)
其中,ci(i=1,…,6)是任意常数.
X1=∂x,X2=∂y,X3=∂t,X4=∂u,X5=y∂u,X6=y2∂u,X7=3x∂x+7y∂y+9t∂t-3u∂u.
(5)
表1中给出了这些生成元(5)的交换子.
表1 李代数的交换表
(6)
从交换表(表1)可以看出,只有两个换位运算不为零,即
[X2,X5]=X4,[X2,X6]=2X5.
(7)
所以,
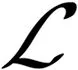
(8)
继续运算,从交换表(表1)中可以看出换位运算均为零,所以有
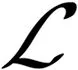
(9)
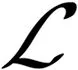
(10)
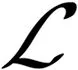
(11)
通过伴随作用可以尽可能地简化系数ki.
经过分析,得到一维子代数最优系统生成元为
(12)
其中,k1,k2,k3,k4是任意常数,ε为±1或0.
表2 李代数的基元素的伴随关系
2 方程(1)的李对称约化
应用优化系统(12)寻找方程(1)的对称约化.这里只以V2=X2+k1X1+εX3为例给出计算过程.限于篇幅,取k1=-1,ε=0,即考虑算子V=∂y-∂x对应的约化.此时,对应的典则坐标为
r=x+y,z=t,u=v(r,z).
(13)
将(13)代入方程(1)得到约化方程:
(14)
可以验证方程(14)拥有的李代数生成元为
Y1=∂r,Y2=∂z,Y3=∂v,Y4=r∂r+3z∂z+(v+z)∂v.
(15)
类似上一节的方法可以得到该李代数的一维子代数最优系统为
U1=m1Y1+m2Y2+m3Y3,U2=Y4,
(16)
其中,m1,m2,m3是任意常数.
不妨取m1=1,m2=-m,m3=1,即考虑算子U=∂r-m∂z+∂v对应的约化,对应的典则坐标为
s=mr+z,v=r+w(s).
(17)
将(17)代入方程(1)积分一次并取积分常数为0,得到
m5w(6)+(1+20m)m2w(4)+20m4w(1)w(4)+120m3(w(1))2w(2)+
12m(1+20m)w(1)w(2)+(121m+8)w(2)+40m4w(2)w(3)=c,
(18)
其中,w(i)(i=1,…,6)分别表示w(s)对变量s的各阶导数.
可以验证该方程(18)通过潘勒韦测试[9-10].
通过截断潘勒韦展开式得到方程(18)如下形式的自贝克隆变换:
(19)
其中,W(s)也满足方程(18).
如果取种子解W(s)=0,并假设:
f(s)=1+eas.
(20)
代入方程(18)可以得到
m5a4+(m2+20m3)a2+121m+8=0.
(21)
由此,得到原方程(1)的一个孤立子解:
(22)
其中,m,a是满足(21)式的任意非零常数.这个解与文献[1]中的已知结果都不同.
3 结语
本文应用李对称方法研究了一个(2+1)-维推广的KdV6方程.首先,找到了保持该方程形式不变的对称无穷小生成元,并借助李代数生成元之间的伴随表示将对应的一维子代数进行等价分类.其次,将原(2+1)-维方程约化为(1+1)维,并进一步讨论了它的对称约化.最终,将原方程转化为一个常微分方程,从而通过求解该常微分方程得到原方程的精确解.限于篇幅,本文只选取特殊的对称约化为例给出计算过程.由于过程的类似性,其余的约化过程可以直接给出结果,将在以后工作中进一步研究.

