基于Adaboost算法的不平衡数据集分类效果研究

董庆伟

(闽南理工学院信息管理学院，福建 石狮 362700)

0 引言

分类问题在实际生活中常见，分类算法的种类也特别多，但由于大多数的分类算法在分类过程中都是针对相对平衡的数据集进行分类，对于数据集不平衡的少类样本没有重点考虑，所以会导致少类样本分类准确率低的现象[1]。而在现实生活中，可能会更需要少类样本分类，比如一万个人中只有几个人患某一罕见疾病，这时候就需要重点分类出这几个样本。因此，需要针对少类样本的特性改善算法，提高不平衡数据集的分类准确率[2]。处理不平衡数据集的分类问题、提高少数类的分类正确率成为当前分类算法设计的研究热点[3]。本文针对不平衡数据集分类过程中产生的不平衡性问题，尝试使用采样技术与传统分类算法相结合的方法，解决不平衡数据集的分类过程中产生的问题。首先使用过采样等技术对数据集进行预处理，产生新的训练样本，在一定程度上解决分类样本的分布不平衡性问题；其次确定基本分类器，采用Adaboost算法对分类器进行学习训练[4]，并输入测试集进行测试，统计分类结果并加以分析(包括准确率和错误率)；最后采用多组数据进行测试，验证此次设计的可行性。

1 Adaboost算法原理与分类方法

1.1 不平衡数据集

不平衡数据集又称非平衡数据集。在一个待分类的样本中，数量较小的一类样本称为少类样本或正类样本，而分布数量较多的那一类样本称为多类样本或负类样本[5]。不平衡数据集因为自身样本分类不平衡的特点，在分类过程中会带来许多问题和难点。

1.2 Adaboost算法

Adaboost算法的思想是：通过改变权值来对基本分类器进行训练和学习，然后把多个分类器算法的核心内容通过改变样本的权重值来实现，对于分类正确的样本就减小权值，对于分类错误的样本则增加权值[1]，这样能在下一次分类过程中着重对分类错误的样本进行分类；将重新分配过权值新训练集送到下层分类器进行新的训练，得到更加精确的分类效果；把每次训练得到的分类器根据一定的原则进行组合，形成一个新的强分类器，作为最后的决策分类器。总体来说，Adaboost算法就是把分类重点放在那些难以分类的样本上面，从根本上解决少类样本的分类难题，提高整体的分类效果。算法整体流程如图1所示。

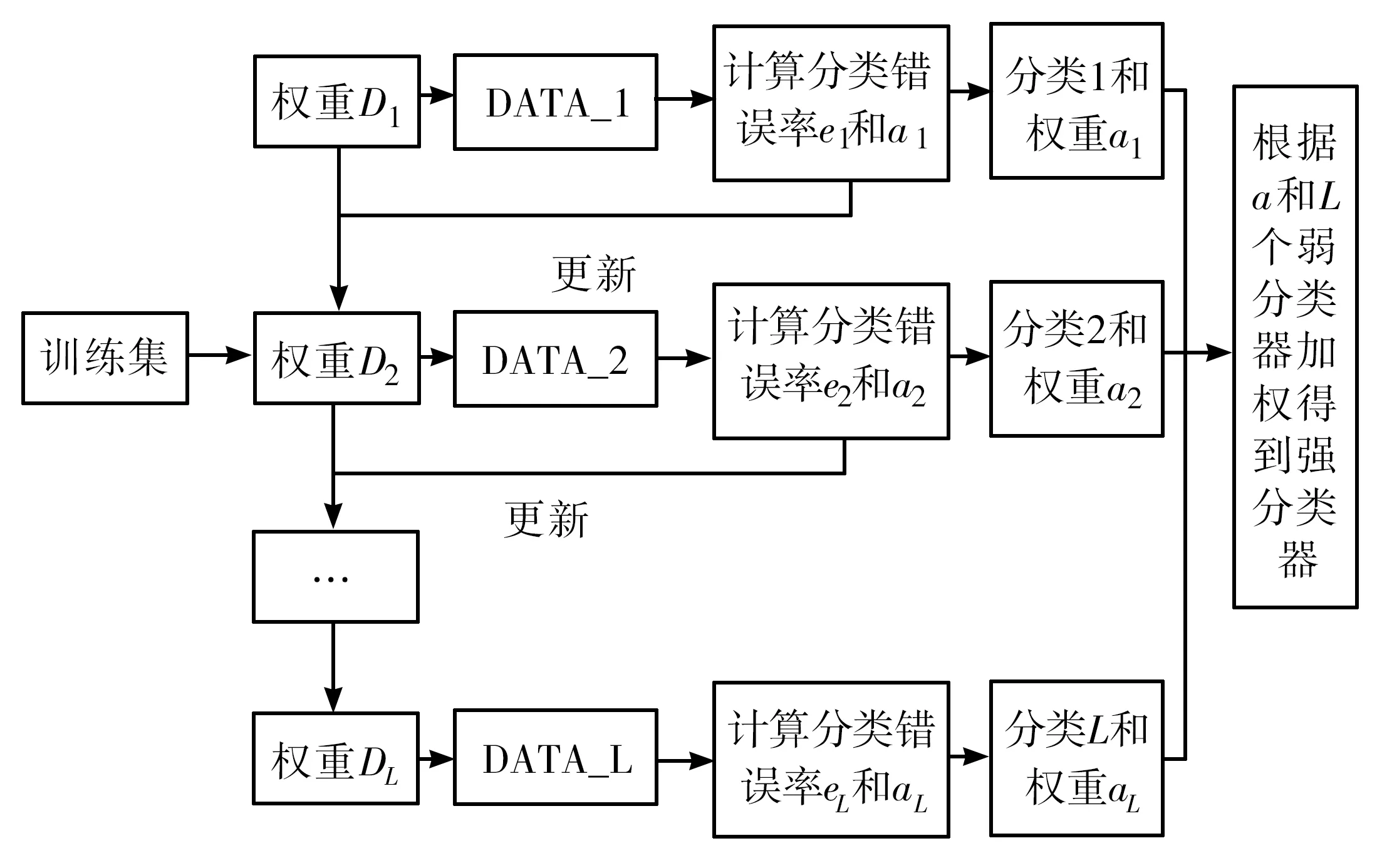
图1 Adaboost算法整体流程图

从图1可以看出，Adaboost算法整个过程可以分为两个部分：第一部分为迭代过程；第二部分为分类器的加权组合过程。第一步，首先将输入的训练集样本权值设为1/N，然后用分类器1进行分类，得出分类错误率和分类权重，根据得到的分类结果和错误率以及权值a来更新样本权值，从而形成新的训练集DATA2；再利用基本分类器2进行分类，同上述一样，再次更新样本权值得到若干基本分类器和权重。第二步就是根据得到的分类器权值a进行加权投票，从而组合成一个强分类器。对不平衡数据集进行一个采样预处理，通过增加少类样本的数量，在一定程度上减缓不平衡数据集的不平衡性，然后用基本分类器学习算法来处理训练集，构建一个强分类器，再用测试集进行测试，得出分类结果并进行分析。

1.3 结果分析指标

1.3.1 精确度

精确度用来衡量一个数据集的总体分类效果，从整体的角度进行衡量，更多地适合用于反应相对平衡的数据集，而不平衡数据集的分类不平衡性则很难进行分类效果衡量。

(1)

其中，TP为被正确分类的正类样本数量；TN为被正确分类的负类样本数量；n+为多类样本数量；n-为少类样本数量。

1.3.2 准确率

准确率是被正确分类的正类样本数量与被分为正类样本数量的比。

(2)

其中，TP为被正确分类的正类样本数量；FP为错误分类的正类样本数量。

1.3.3 召回率

召回率反映的是被正确分类的正类样本数量与所有样本数量的比。

(3)

其中，TP为被正确分类的正类样本数量；FN为错误分类的正类样本数量。

1.3.4 不平衡率

不平衡率是被正确分类的正类样本数量与所有样本数量的比。

(4)

其中，TP为被正确分类正类样本数量；n+为多类样本数量；n-为少类样本数量。

2 实验结果

2.1 实验数据

本文采用Adaboost算法得到实验数据，数据集包括：第一组数据为demo数据集，随机产生200个样本，样本维度为2；第二组为heart数据集，共有100个样本，样本维度为13；第三组为下载的usps数据集，共1 000个样本，样本维度为256。分别对以上数据进行分类测试。

2.2 实验数据测试

分别使用Adaboost算法和单层决策树(decision stump)对三组数据进行测试，测试结果如表1所示。数据不同，其样本分布不同；数据分布的不平衡影响最终的分类准确率。从表1可以看出，不平衡率越大的数据集，分类准确率越低。本文方法在一定程度上能够提高分类效果，由于样本数量不同，所得到的分类效果也不同。总体来说，测试集和训练集的分类准确率会随着迭代次数、样本数量的增大而提高。从实验结果来看，随着样本不平衡率的提高，样本分类准确率会相对降低，这是由不平衡数据集的不平衡特点所引起的，而本文采用的Adaboost算法在一定程度上能够减缓样本不平衡所带来的问题。

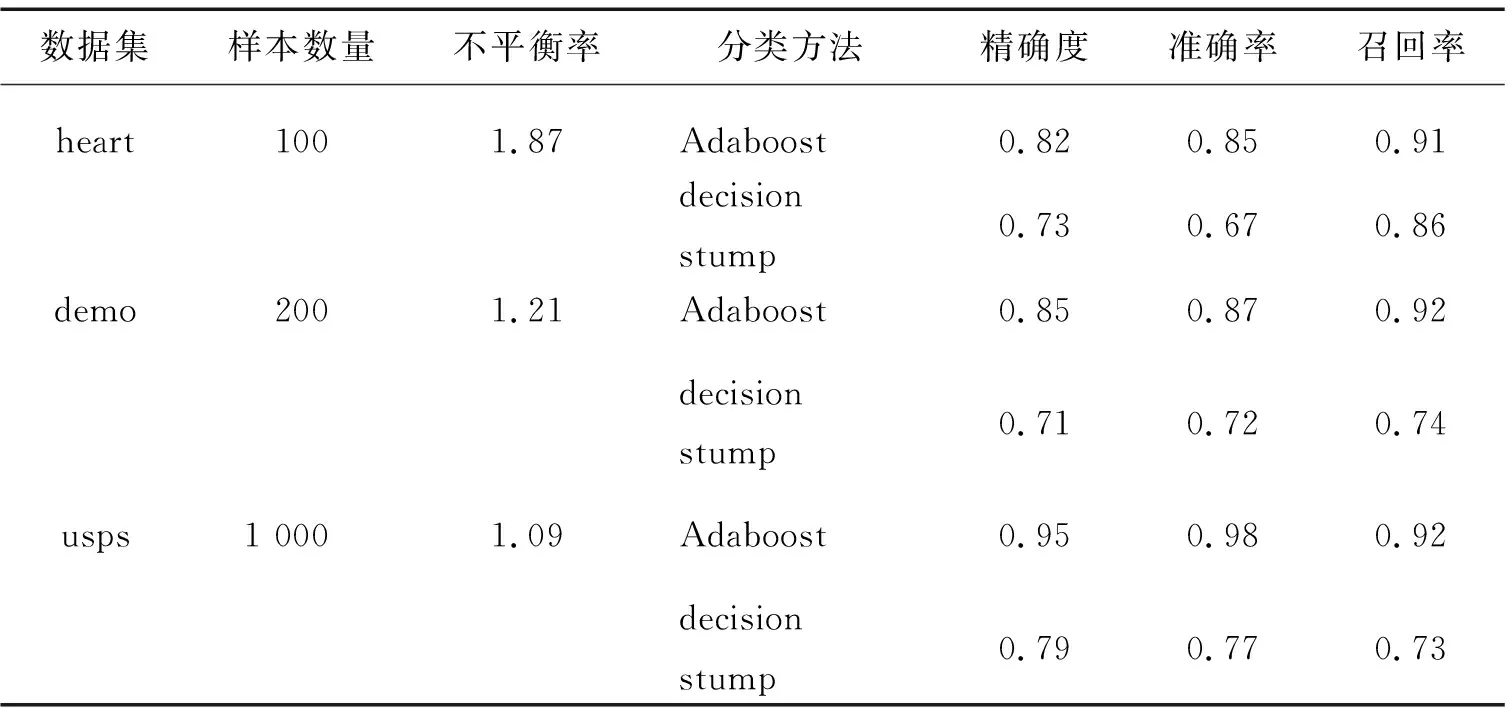
表1 不同样本得到的分类准确率统计结果

2.3 迭代次数对Adaboost算法分类的影响

图2为训练集和测试集错误率变化图，其中，y轴代表训练集和测试集的分类错误率，x轴代表分类器迭代次数。不同的数据集样本平衡度不同，其得到的测试样本分类准确率也不同，而其随着迭代次数的变化而变化。随着迭代次数的增加，训练集错误率总体呈逐渐降低趋势。由于训练集是用来训练分类器学习的，所以其准确率要比测试集的准确率要高[5]。不仅迭代次数能够引起错误率的变化，同样地，训练样本的数量也影响着最终的分类效果：随着样本数的增加，错误率将明显降低。此外，由图2(b)可以看到，分类错误率并不是一直降低，这是由于Adaboost算法在训练过程中特别容易受到噪声数据和异常数据的影响，结合基本分类器加权组合的特性，导致迭代过程中错误率不是一直降低。

(a)demo数据集

(b)heart数据集

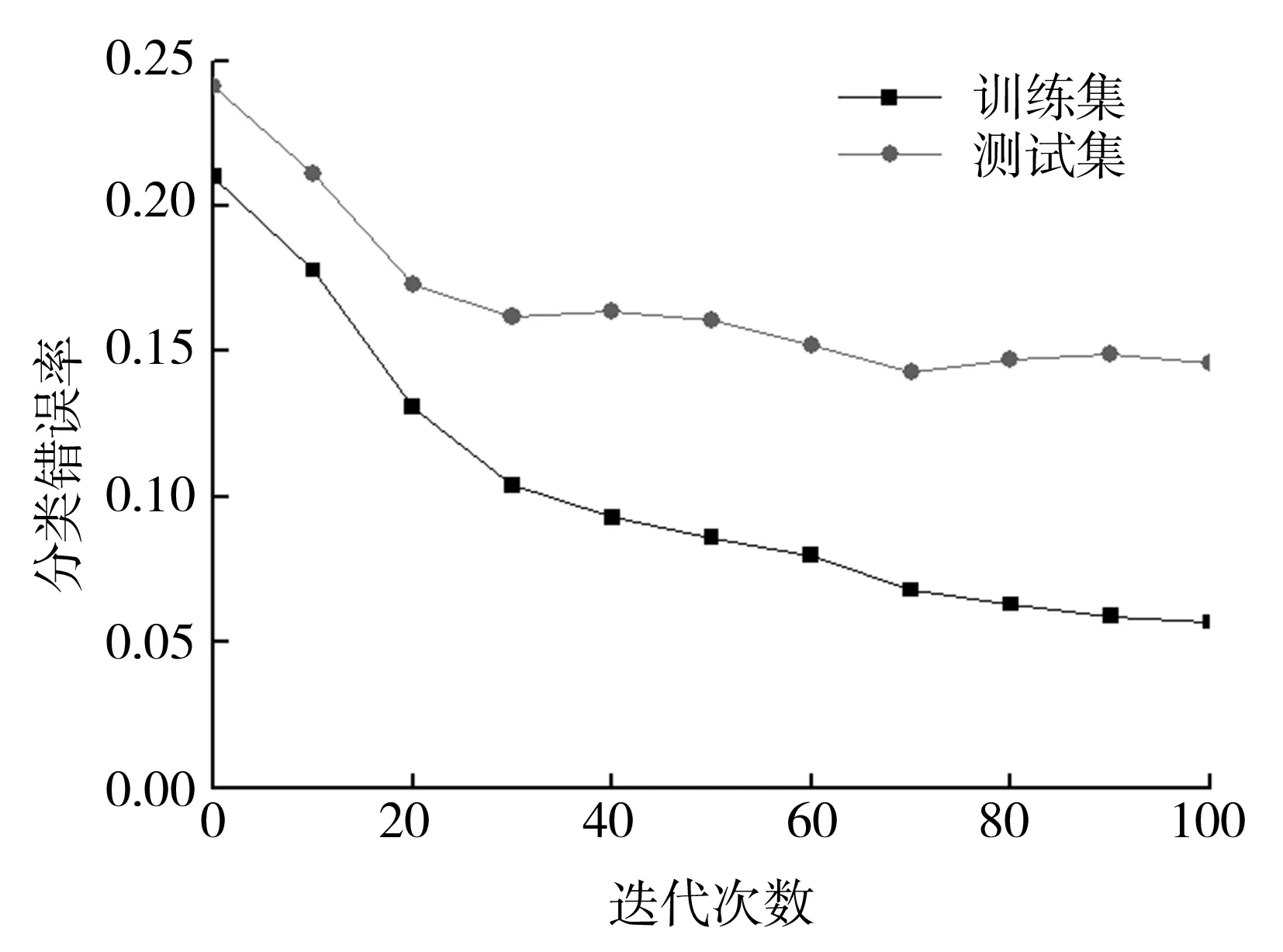
(c)usps数据集图2 训练集和测试集分类错误率变化图

3 结语

本文首先通过SMOTE算法采样对不平衡数据集进行一个预处理，然后确定采用单层决策树作为基本分类器，最后进行Matlab编程，构建Adaboost算法分类器。得到如下结论：随着样本数的增大，数据集的分类准确率升高；随着数据集不平衡率的增大，分类准确率会有所降低，但相较于传统的单层决策树算法而言，准确率有非常明显的提升，平均分类准确率在85%以上；随着迭代次数的增加，训练集错误率总体呈逐渐降低趋势；通过改变正类样本的权值，重视对少类样本的分类，能够在一定程度上提高整体的分类效果。