Ca-RG、Sr-RG与Hg-RG系统约化势的理论研究

魏丽敏

(西安航空学院 理学院，西安 710077)

1 研究背景与主要内容

随着激光技术、天体物理、新材料、光化学等重要学科的发展，分子间势函数的研究引起了学术界越来越多的重视。双原子分子势函数是对双原子分子结构的完全描述，在正确描述双原子分子电子本征能量的同时，又可作为多原子分子势能函数的多体项展式中的两体项，它是研究多原子分子势函数的基础[1]。由两个满壳层原子(第IIA族碱土金属原子Mg、Ca、Sr、Ba，第IIB族原子Zn、Cd、Hg以及第零族稀有气体原子He、Ne、Ar、Kr、Xe)构成的双原子体系，原子间由于瞬时偶极矩相互耦合而形成一个弱相互作用van der Waals键，组成分子的两个原子基本上保持了原来的电子结构，它们基态的结合能很弱，这时应用量子力学从头计算法，由两个大物理量相减来算得如此弱的结合能会造成较大的误差，而且应用量子力学来计算分子势能函数很复杂又很费时。因此，很有必要寻求相对简单而又可靠的势模型对这类分子体系基态的结合能(van der Waals势)进行研究。

1984年，Tang K T和Toennies J P教授从原子间相互作用的物理本质出发，提出了著名的描述van der Waals双原子分子势函数的Tang-Toennies势模型[2](简称TT势)。该模型很好地考虑了双原子体系的库仑排斥作用，电子交换作用，长程色散以及电子云重叠效应等，仅需五个参数就可以描述分子全程区域的势能曲线，已成功的用于计算很多双原子体系准确的相互作用势[3-11]。对于Zn-RG(RG=He、Ne、Ar、Kr、Xe)系统各双原子分子的基态van der Waals势，能找到的相关实验信息特别少，而理论计算结果之间也存在特别大的差距，所以我们很有必要探索是否能够应用TT势来描述各分子的势能曲线。

在文献[7]中，作者得到了这样的结论： Sr2、Ca2和Hg2双原子分子的约化势曲线几乎完全一致，但是不同于Ar2和Kr2的重合约化势曲线；Sr-RG各分子的约化势曲线一致。另外，在文献[6]中，作者计算得到了Ca-RG系统各分子的TT势能曲线，但是约化势曲线未给出。在文献[8]中，作者计算得到了Hg-RG系统各分子的TT势能曲线，并且各分子的约化势曲线几乎完全重合。本文先验证了Ca-RG系统各分子的TT约化势曲线形状相同，然后比较了Ca-RG、Sr-RG与Hg-RG各系统的约化势曲线是否存在差别。如果不存在差距，那么我们就可以假设Zn-RG和Cd-RG系统各双原子分子的van der Waals势能曲线,也可以用TT势模型描述并且满足对应态原理，这些分子约化势分别与Hg-RG系统各分子的约化势共形，就可以从共形分子(约化势形状相同的分子)的约化势参数出发，来得到Zn-RG和Cd-RG系统各分子的约化势参数，并最后转换为各分子的TT势参数。这个想法的来源是约化势要比实际的势能相近得多，应用于约化势参数的组合规则要更为准确。

2 计算方法

2.1 Tang-Toennies势模型

Tang和Toennies教授在1984年提出了著名的描述van der Waals双原子分子势函数的Tang-Toennies势模型[2]：

其中，A、b为排斥势参数，C2n为色散系数，nmax一般情况下取nmax=5就足够，更高阶项对势能的影响很小。势模型中的参数都具有相应的物理意义，排斥势参数A和b也不需要利用从头算来得出，可由Re、De、C6、C8、C10的值反推得到相关结果[12]，其中Re为平衡间距，De为势阱深度。TT势的精确度较高，是一种非常重要的双原子分子势函数模型，也可以推广用于描述原子与离子XY+间的势能函数[13]。直到1991年，Tang和Toennies教授仍在对TT势模型作进一步的改进和完善[14]。 TT势函数是一个解析式，各阶导数都存在，因此可以方便地用于需要解析扩展到复平面的理论。

2.2 对应态原理

对应态原理最早是由van der Waals在1880年提出的，他分别用体积、温度和压力的值除以它们各自的临界值，得到了一个具有普遍性的状态方程。由于一个体系的状态可以由上述三个参数中的任意两个来描述，对应态原理表示所有的物质都遵循相同的由两个约化参数形式给出的状态方程[15]，是一种非常实用的物理研究方法[16]。

1938年，De Boer和Micherls[17]以及稍晚的Pitzer[18]给出这样的结论：如果以V(R)=DeU(R/Re)的势函数形式来描述分子势能时，是满足对应态原理的。其中，U(x)为势能的约化形式，R为核间距，Re为平衡间距，De为势阱深度。例如，大家熟知的Lennard-Jones(12-6)势的约化形式为U(x)=x-12-2x-6。这样，两种不同分子各自的相互作用势可以用不同的Re和De值由LJ(12-6)势模型给出，满足对应态原理，也可以表述为这两种分子的约化势是共形的。后来，通过对精确的实验数据分析，发现并不是所有的物质的势能曲线都满足对应态原理。但是，在高精度范围内，所有稀有气体同核双原子间的势能约化形式是一致的，只是这种约化形式不能用先前使用的简单势函数，如LJ(12-6)或Morse势来描述。

TT势模型能精确地描述稀有气体21种同核及异核双原子间的相互作用势[4]，而且结果还证明这些分子满足对应态原理，它们的约化势相互共形。后来，TT势被用于描述Ca-RG[6]、Sr-RG[7]和Hg-RG[8]系统各分子的van der Waals势，并且Sr-RG与Hg-RG各系统的约化势分别共形。

2.3 Tang-Toennies约化势

在TT势模型中，令：

x=R/Re

(2)

U(x)=V(Rex)/De

(3)

则势函数的约化形式为：

其中：

b*=bRe

(6)

在势阱位置，即R=Re(x=1)处，约化势满足以下条件：

U(x)=-1

(8)

3 结果与分析

研究者已对Ca-RG、Sr-RG与Hg-RG系统各分子基态的van der Waals势作了详细的研究[6-8]，各分子的TT势参数是已知的，本次计算以这些分子的TT势参数作为计算的基础数据，并列于本文的表1～表3中。

表1 Ca-RG系统各分子的TT势参数 单位：a.u.

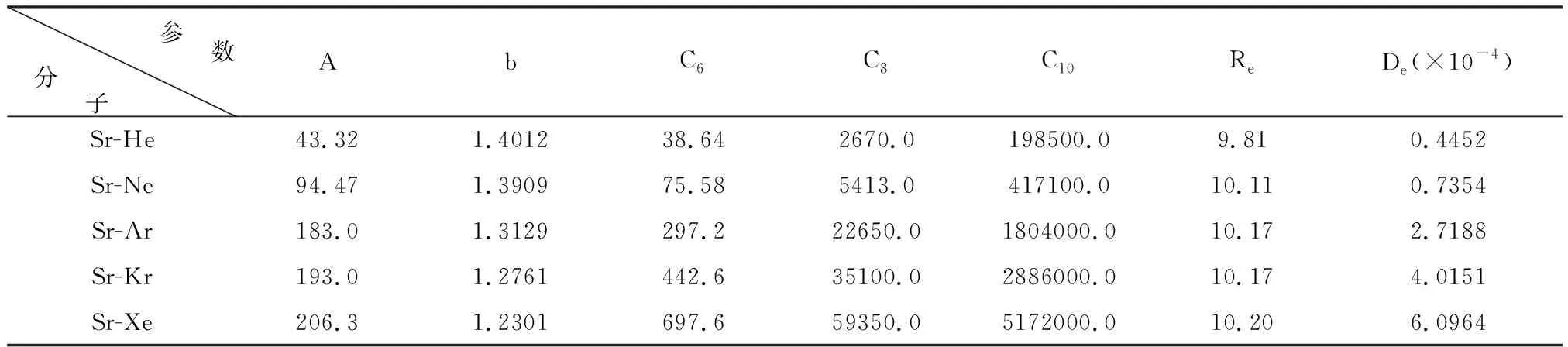
表2 Sr-RG系统各分子的TT势参数 单位：a.u.

表3 Hg-RG系统各分子的TT势参数 单位：a.u.

从表1～表3中可以看到，各个系统中各双原子分子的势能参数差距相当地大，比如说Ca-RG系统中，Ca-He 与Ca-Xe分子的色散系数C6相差16倍之多。表4中列出的是通过(5)～(7)式计算得到的Ca-RG系统各分子的约化势参数，从此表中可以看到Ca-He、Ca-Ne、Ca-Ar、Ca-Kr、Ca-Xe这五种异核双原子分子各对应的约化势参数都基本上相同，比表1中的势参数要彼此接近的多很多，与Ca-He 与Ca-Xe分子的约化色散系数C6*几乎完全一致。尽管它们不是完全相同，但是在排斥区的微小差距可以由吸引区的差别补偿，所以作U(x)-x图时，从图1中可以看到，这五条约化势曲线是完全重叠在一起的，这种势能曲线的不变性并不是使用相同势模型的结果。Sr-RG与Hg-RG系统各分子基态的TT约化势在这里就不再给出，结果与Ca-RG系统的情况一致，各系统的约化势分别重合在一起。

表4 Ca-RG系统各分子的TT约化势参数

图1 Ca-RG系统各分子的约化势曲线

为了比较这三个系统各自重合的约化势曲线有何区别，本文分别给出了它们之间的比较图，为了清晰可辨，分别画在了图2中的五幅图中。从图2中可以看到，虽然是不同的双原子分子的约化势曲线比较图，但这五幅图的曲线形状几乎一模一样，Ca-RG与Sr-RG系统的约化势曲线完全重合，而Sr-RG系统各分子的约化势曲线与Ca-RG、Sr-RG系统对应分子的约化势曲线稍有差别，在长程区范围要稍微深一些。

(a) (b) (c)

(d) (e)

图2Ca-RG、Sr-RG和Hg-RG系统的约化势曲线比较

Ca与Sr原子同属于第IIA族，而Zn、Cd、Hg原子同属于第IIB族，既然Ca-RG和Sr-RG系统各分子的TT约化势曲线完全吻合，我们假设Zn-RG和Cd-RG系统各双原子分子的van der Waals势能曲线也可以用TT势模型描述并且满足对应态原理，那么这些分子约化势分别与Hg-RG系统各分子的约化势共形来构建Zn-RG和Cd-RG系统各分子势函数的计算方法是合理可行的。

本文的计算结果表明，对应态原理的实用价值，同时也期望本文的研究结果能够提供有效的关于更多体系的异核相互作用势的计算方法，对今后势模型的研究以及组合规则的建立起到一定的指导意义。