具有时延的离散二阶多智能体系统的一致性问题
韩摩西,胡卫敏,谢冬梅
(1.伊犁师范大学数学与统计学院,新疆 伊宁 835000;2.伊犁师范大学应用数学研究所,新疆 伊宁 835000;3.天津大学数学学院,天津 300350)
0 引言
HU[1]、TIAN[2]、YANG[3]等考虑领航者和跟随者采用自身状态带有时延的算法,给出了关于时延的一致性条件.受到HU等[1]的启发,韩摩西等[4]研究了在固定拓扑下带有时延的二阶多智能体系统的一致性问题,系统动态模型和控制协议如下:
对于系统中含有1个领航者、n个跟随者的多智能体系统,第i个跟随者的动态为
(1)
领航者的动态可以被描述为
其中,xi(t),vi(t),ui(t)∈R,分别表示第i个智能体的位置、速度和控制输入.因此,对于第i个跟随者,一个基于邻接顶点连接的控制协议可表示为
(2)
最后利用Hopf分支理论得到系统达到一致的充分条件.
1 预备知识及问题描述
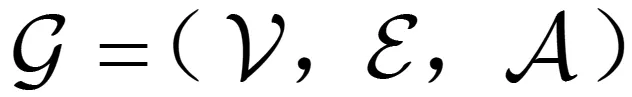
定义B∶=diag{b1,b2,…,bn}为领航者与跟随者之间的邻接矩阵,bi>0表示领航者与第i个智能体之间有连接,否则bi=0.
本文将上述连续时间系统的研究内容推广到离散时间系统,对于系统中含有1个领航者、n个跟随者的多智能体系统,第i个跟随者的动态为
xi(d+1)=xi(d)+vi(d),vi(d+1)=vi(d)+ui(d),i∈I,
(3)
其中,xi(d),vi(d),ui(d)分别表示第个智能体的位置、速度和控制输入.d表示系统在离散时间下的第d时刻,d∈N*.
领航者的动态可以被描述如下:
x0(d+1)=x0(d)+v0,
其中,x0(t)表示领航者的位置,x0(t)∈R;v0表示领航者的速度为常数,v0∈R.
因此,对于第i个跟随者,一个基于邻接顶点连接的控制协议可表示为
(4)
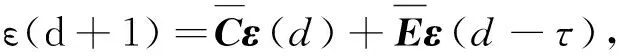
(5)
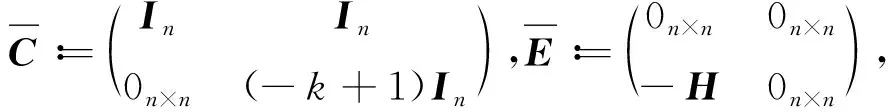
经过变量代换,系统(3)在控制协议(4)下的一致性问题,可转化为系统(5)的稳定性问题,因此,接下来主要研究(5)的稳定性.

注 Jury稳定判据是关于实系数特征多项式的稳定性判据,并不能判断系数是复数的特征多项式的稳定性.
引理2[6]多项式r(σ)是Hurwitz稳定的当且仅当m(ω)和n(ω)的大小是相互交替的,且m(0)n′(0)-m′(0)n(0)>0,其中,m(ω)和n(ω)分别是多项式r(iω)中的实部项的和与虚部项的和组成的多项式(这里r(iω)是令r(σ)中σ=iω得到的多项式).
引理3[7](Jensen不等式) 对于给定的常数d>0,存在正定对称矩阵R>0和函数x(k),y(k),k=1,2,…,其中,x(k),y(k)满足y(k)=x(k+1)-x(k),则有下面不等式成立:
2 主要结果
当系统对应的拓扑图为无向图时,且系统不带有时延,即系统中τ=0时,有
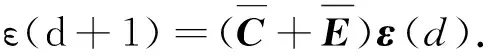
(6)
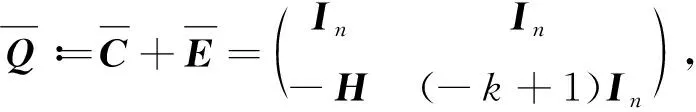

其中,λi∈Λ(H).


(ii)m1 将ri(u)改写成如下形式: 这里只需研究ri(u)的Hurwitz稳定性.令u=iω,可得到 分离上式的实部和虚部m(ω),n(ω),得到 下面利用引理2判别ri(u)的Hurwitz稳定性. 二次方程m(ω)均有两个不同实根,当且仅当m(ω)的判别式Δm(ω)>0,即 根据引理2,还需满足m(ω),n(ω)的根的大小相互交替,求解m(ω),n(ω)得到 因此,应满足m1>n1>m2,即 需满足m(0)n′(0)-m′(0)n(0)>0.由m(ω),n(ω)得到 则有 即满足 当系统对应的拓扑图为有向图时,且系统带有时延,即系统中τ>0时,研究的是系统(5)的稳定性. 定理3 对于系统(5),即存在对称正定矩阵P,S∈Rn×n,满足下述条件: 则可保证系统(5)是Schur稳定的. 证明 根据引理3,定义Lyapunov函数: 其中,P,S均为正定矩阵,因此V(d)是正定的.V(d)的向前差分为 ΔV(d)=V(d+1)-V(d)= εT(d+1)Pε(d+1)-εT(d)Pε(d)+ εT(d)Sε(d)-εT(d-τ)Sε(d-τ)= εT(d)Pε(d)+εT(d)Sε(d)-εT(d-τ)Sε(d-τ)= εT(d-τ)ETPEε(d-τ)= 因此,如果 则ΔV(d)<0.根据李雅普诺夫稳定性理论,系统(5)是Schur稳定的. 定理4 对于系统(5),存在适当维数的正定矩阵P,Q,S,使得 那么系统(5)渐近稳定. 证明 根据引理3,定义变量y(d)=ε(d+1)-ε(d),构造如下形式的Lyapunov-Krasovskii泛函: V(k)=V1(k)+V2(k)+V3(k), 那么, ΔV1(k)=V1(k+1)-V1(k)=εT(d+1)Pε(d+1)-εT(d)Pε(d)= ΔV2(k)=V2(k+1)-V2(k)=εT(d)Qε(d)-εT(d-τ)Pε(d-τ), ΔV3(k)=V3(k+1)-V3(k)= 由引理3可得, ΔV3(k)=V3(k+1)-V3(k)= 则有 ε(d-τ))T. 如果 则ΔV(d)<0.根据李雅普诺夫稳定性理论,系统(5)是渐进稳定的,即系统(3)在控制协议(4)下能达到一致.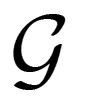



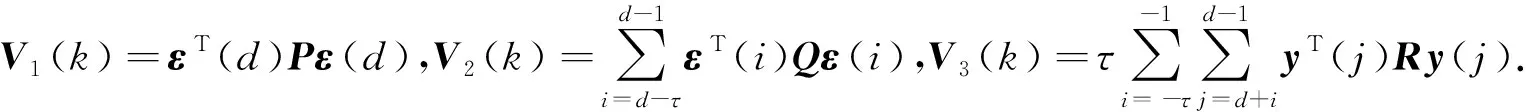
—— 瓮福集团PPA项目成为搅动市场的“鲶鱼”

