NA序列部分和之和乘积的极限定理
李雪峰, 陆冬梅
(长春电子科技学院, 长春 130114)
1 引言及主要结果
定义1[1]如果对于集合{1,2,…,n}的任意两个不相交的非空子集T1和T2, 均有
Cov(f(Xi,i∈T1),g(Xj,j∈T2))≤0,
则称随机向量X=(X1,X2,…,Xn)为负相关的(negatively associated, NA), 其中f和g是任意两个使得协方差存在且对每个变元均非降(或均非升)的函数.如果对任意的n≥1, (X1,X2,…,Xn)为NA的, 则称随机变量序列{Xn,n≥1}为NA序列.
NA随机变量在可靠性理论、 渗透性理论及多元分析中应用广泛[2]. 目前, 关于NA随机变量性质的研究已有许多结果[3-11].设{Xn,n≥1}是均值为1的独立同分布指数随机变量序列, 文献[12]证明了:

(1)
利用Stirling公式, 式(1)等价于


(2)
本文中N均为标准正态随机变量.由定理1可得以下推论:

注1定理1的结果推广了文献[14]的结果, 即从NA序列部分和乘积推广到NA序列部分和之和乘积.
假设条件:
(H1)g(x)为[n0,∞)上具有非负导数g′(x)的正值可导函数, 且g(x)↑∞,x→∞;


定理2在定理1的假设条件下, 如果假设条件(H1)和(H3)成立, 则对于s>0, 有

(3)
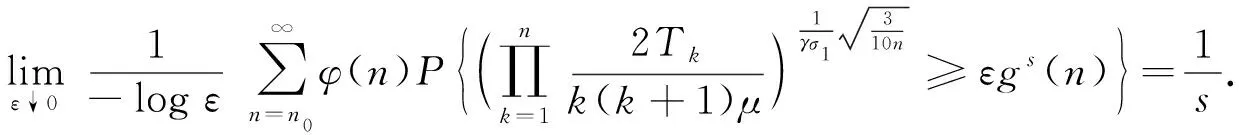
(4)


(5)
由定理2和定理3可得以下推论:

注2定理2和定理3的结果推广了文献[19]的结果, 即从ρ-混合序列部分和之和乘积精确渐近性推广到NA序列部分和之和乘积精确渐近性.
注3满足假设条件(H1)~(H3)的g(x)有很多, 例如g(x)=xα,(logx)β,(log logx)γ, 其中α>0,β>0,γ>0为某些适当的参数, 下列推论是一些经典的实例.
推论3在定理2中取g(n)=n(2-p)/(2p),s=1, 其中1≤p<2, 则有
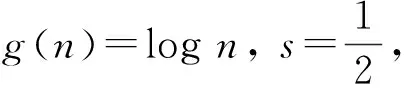
推论5在定理2中取g(n)=log logn,s=d, 其中d>0, 则有


推论8在定理3中取g(n)=loglogn,s=d,t=1-b, 其中0
2 主要结果的证明
2.1 定理1的证明

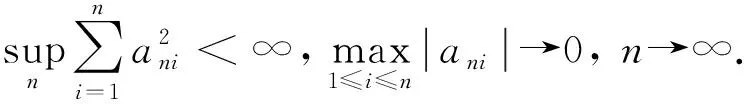

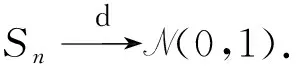
引理2[3]设{Xn,n≥1}为一严平稳NA随机变量序列, 满足

n-1/pTn→0, a.s.n→∞.
引理3[3]在定理1的假设条件下, 有

(6)
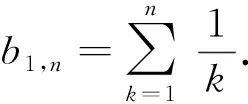
下面证明定理1.当x>-1时, 有
log(1+x)=x+xθ(x),
其中当x→0时,θ(x)→0.则有
由引理2(取p=2)以及θ(x)→0可知, 当x→0时, 有
另一方面, 由引理3可知,
利用Markov不等式, 可得

(8)
从而由式(7)和式(8)以及Slutsky引理知, 要证式(2)成立, 只需证明下式成立即可:

(9)

从而
即引理1的条件都满足, 进而式(9)成立, 定理1得证.
2.2 定理2的证明
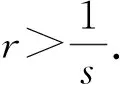
引理4[21]在定理2的假设条件下, 有
引理5在定理2的假设条件下, 有
证明: 只需证明式(10)成立, 式(11)类似可证.由定理1可知
注意到
因此由Stolz定理, 可得
引理6[21]在定理2的假设条件下, 有
引理7在定理2的假设条件下, 有
证明: 显然, 由式(13)成立可推出式(12)成立, 因此只需证明式(13)成立即可.注意到要证式(13)成立, 只需证明下式成立:
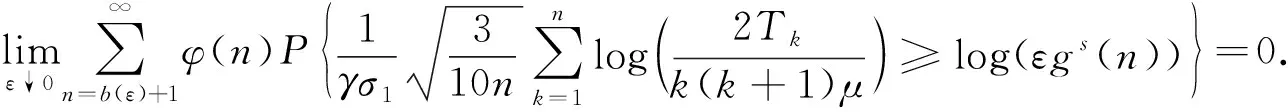
(14)
由于对任意的x>-1, 有log(1+x)≤x, 从而要证式(14)成立, 只需说明下式成立即可:
由n>b(ε)可推出εgs(n)>ε1-rs, 通过简单交换求和次序可知

(15)
下面证明定理2.由引理4~引理7以及三角不等式可知定理2成立.
2.3 定理3的证明
记d(ε)=[g-1(Mε-1/s)], 其中g-1(x)为g(x)的反函数,M≥1.
引理8[21]在定理3的假设条件下, 有
引理9在定理3的假设条件下, 有
证明: 注意到0 注意到 由Stolz定理可得 引理10[21]在定理3的假设条件下, 有 引理11在定理3的假设条件下, 有 (16) 证明: 由于对任意的x>-1, 均有log(1+x)≤x, 因此要证式(16)成立, 只需说明下式成立即可: 下面证明定理3.由引理8~引理11以及三角不等式可知定理3成立.


