Hilbert空间下CAANA序列的完全矩收敛

费丹丹, 付宗魁, 李彩娟

(信阳学院 数学与统计学院, 河南 信阳 464000)

1 引言与预备知识

定义1[1-2]若存在非负序列{q(m),m≥1}满足q(m)→0,m→0, 且对任意的m,k≥1, 有

Cov(f(Xm),g(Xm+1,Xm+2,…,Xm+k))≤q(m)(Var(f(Xm))Var(g(Xm+1,Xm+2,…,Xm+k)))1/2,

则称随机变量序列{Xn,n≥1}是AANA(asymptotically almost negatively associated)的, 其中f,g是关于每个变元单调非降的连续函数, 并且存在方差, {q(m),m≥1}称为该AANA序列的混合系数.

显然, AANA序列包含了独立序列和NA序列[2]. 由于AANA序列在金融保险、 可靠性分析、 多元统计分析和时间序列分析中应用广泛, 因此已得到广泛关注, 并且取得了一系列研究结果. 例如： Wang等[3]研究了AANA序列的强大数律和重对数律； Yuan等[4]得到了AANA序列的Rosenthal型不等式； Shen等[5]讨论了AANA序列的强收敛性； Xi等[6]得到了AANA随机变量的完全矩收敛; Ko[7]将AANA的概念拓展到Hilbert空间. 设(H,‖·‖)为实可分Hilbert空间, 其中‖·‖=〈·,·〉， 〈·,·〉表示内积.设{ej,j≥1}为H中单位正交向量序列, 若X为H值随机向量, 则X(j)=〈X,ej〉.

定义2[7]若存在H中单位正交序列{ej,j≥1}, 使得对任意的d(d≥1)维序列{(〈Xi,e1〉,…,〈Xi,ed〉),i≥1}是AANA的, 则称H值随机向量序列{Xn,n≥1}是AANA的.

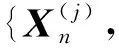
完全收敛性的概念由Hsu等[8]提出, Chow[9]对其进行了深入研究, 给出了完全矩收敛的概念, 这些研究成果目前已成为概率极限理论中的重要内容. 例如： 文献[10-12]研究了独立和混合相依序列实值情形的结果； 文献[13-15]讨论了关于Banach空间值情形的结果； 文献[7,16-19]得到了Hilbert空间H值情形的结果. 特别地, Sung[12]研究了NA序列的完全收敛性, 得到如下结果：

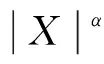
本文在Sung[12]研究结果的基础上, 考虑Hilbert空间下不同分布CAANA序列的完全矩收敛, 所得结果推广并改进了Sung[12]的结论.

定义4[20]设{X,Xn,n≥1}为H值随机向量序列, 若存在正常数C, 使得

则称{Xn,n≥1}正交弱一致有界于X.简记为{Xn,n≥1}X.

本文C在不同之处表示不同的常数, a.s.表示几乎处处,I(A)表示集合A的示性函数, logx=ln max{x,e}, ∀x∈.

2 引 理

引理1[5]设{Xn,n≥1}是混合系数为{q(n),n≥1}的AANA随机变量序列, 若{fn(·),n≥1}为单调不增(或单调不减)的函数序列, 则{fn(Xn),n≥1}仍是混合系数为{q(n),n≥1}的AANA随机变量序列.

引理3[21]设{X,Xn,n≥1}为任意的随机变量序列, 若存在正常数C, 使得

则对任意常数a>0,b>0,C1>0,C2>0, 下列不等式成立：

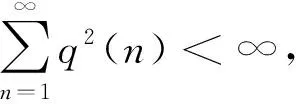
(1)

其中bn=n1/α(logn)1/γ,X(j)=〈X,ej〉.

证明: 对∀n,i,j≥1, 记

首先, 证明

(2)

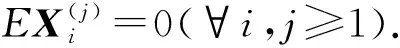
由式(3)和式(4)知式(2)成立.对充分大的n, 有

于是, 为证式(1)成立, 只需证H1<∞,H2<∞.

对H1, 由Markov不等式、 引理3和α/γ>1, 得

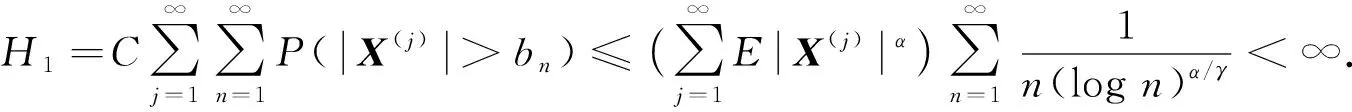
(6)

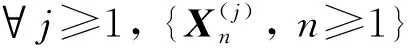
证毕.

3 主要结果

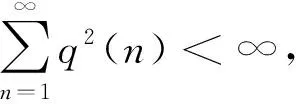
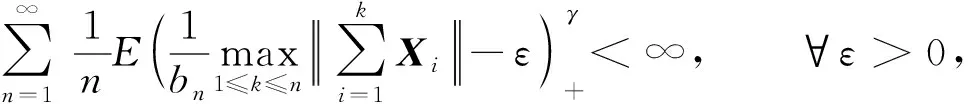
(8)

其中bn=n1/α(logn)1/γ,X(j)=〈X,ej〉.

证明: 对∀n,i,j≥1, 记

对∀ε>0, 由式(8)知

为证式(8)成立, 由式(1)知只需证

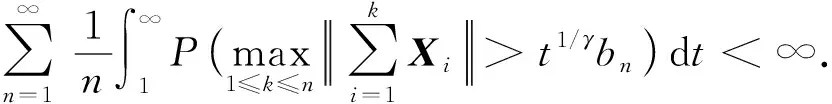
(9)

对式(9), 易得

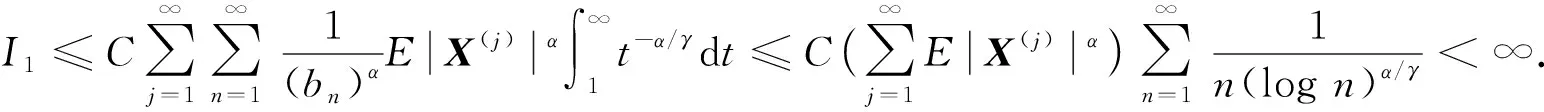
(10)

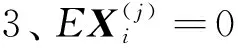
由式(10)～(13)知式(9)成立.证毕.

注1若{X,Xn,n≥1}是混合系数为{q(n),n≥1}的同分布H值CAANA随机向量序列, 则定理2仍然成立.

注2若{X,Xn,n≥1}是同分布H值CNA(coordinatewise negatively associated)随机向量序列和独立随机向量序列, 则定理2仍然成立.

证明: 为证式(8)成立, 只需证式(1)和式(9)成立.先证式(1)成立, 由γ<α和1/2<α<2得

下面证式(9)成立, 由γ<α和1/2<α<2知

因此, 式(8)成立.