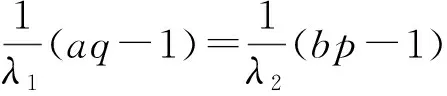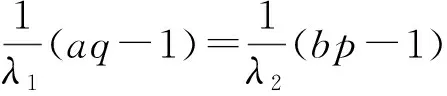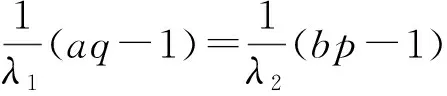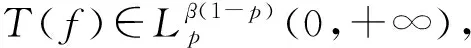非齐次核逆向Hilbert型积分不等式的最佳搭配参数及算子表达式
洪 勇, 陈 强
(1. 广州华商学院 应用数学系, 广州 511300; 2. 广东第二师范学院 计算机学院, 广州 510303)
1 引言与预备知识
设1/p+1/q=1(p>1), Hardy等[1]给出了Hilbert不等式:

(1)
通过引入参数λ将式(1)推广为

非齐次核K(x,y)=G(xλ1yλ2)(λ1λ2≠0)显然具有如下性质: 若t>0, 则
K(tx,y)=K(x,tλ1/λ2y),K(x,ty)=K(tλ2/λ1x,y).
为避免重复, 引入记号:

引理1[23]设Ωn⊆n,x=(x1,x2,…,xn), 1/p+1/q=1(0 当且仅当存在非零常数C, 使得fp(x)=Cgq(x)(x∈Ωn)时等号成立. 与文献[22]相应引理的证明方法类似可得: 引理2设1/p+1/q=1(0 设1/p+1/q=1(0 A(K,|f|,|g|)≥M(a,b)‖f‖p,α(a,b)‖g‖q,β(a,b). (2) 若式(2)的常数因子M(a,b)是最佳值, 则称a,b为最佳搭配参数. 定理1设1/p+1/q=1(0 (3) (4) 其中W0=|λ2|W1(-bp)=|λ1|W2(-aq). 2) 若W1(-bp)<+∞,W2(-aq)<+∞, 且存在σ>0, 使得W1(-bp+σ)<+∞或W1(-bp-σ)<+∞, 则下列命题等价: 证明: 1) 根据逆向的加权Hölder积分不等式和引理2, 有 且经简单计算可得α=apq-1,β=bpq-1, 故式(3)可化为式(4). 当W1(-bp-σ)<+∞时, 取充分小的ε>0, 令 则 于是可得 从而 (5) 当W1(-bp+σ)<+∞时, 取充分小的ε>0, 令 则有 于是有 从而 (6) 则 于是式(3)等价于 由于式(3)的常数因子是最佳的, 故式(7)的常数因子也是最佳的. 因为式(7)的常数因子是最佳值, 故由式(7)和式(8), 可得 从而W1(-b′p))<+∞,W2(-a′q))<+∞.又因为 故根据②⟹①的证明可知, 式(7)的最佳常数因子为 于是可得 (9) 根据逆向Hölder积分不等式, 有 ②⟹③.根据引理2可得. 设1/r+1/s=1(0 若λ2c>0, 则-λ2cs>0, 此时有 令s→-∞, 有W1(-bp)=+∞, 这与W1(-bp)<+∞矛盾.若λ2c<0, 则-λ2cs<0, 此时有 令s→-∞, 得W1(-bp)=+∞, 仍与W1(-bp)<+∞矛盾. 设K(x,y)≥0, 定义积分算子T: (11) 根据Hilbert型积分不等式的基本理论, 逆向Hilbert型积分不等式(2)等价于算子不等式: ‖T‖p,β(a,b)(1-p)≥M(a,b)‖f‖p,α(a,b), 由此并根据定理1, 可得如下关于积分算子的结果. 定理2设1/p+1/q=1(0 (12) 其中W0=|λ2|W1(-bp)=|λ1|W2(-aq). (13) 综上并根据定理2可知, 例1结论成立.


2 最佳搭配参数的等价条件
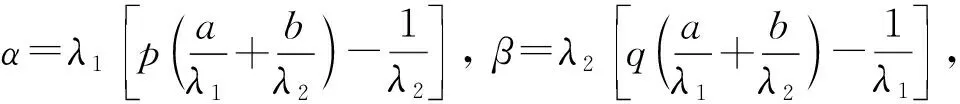
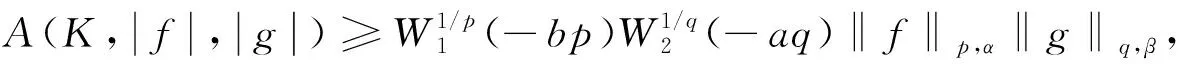

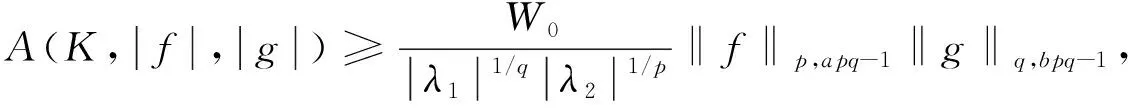






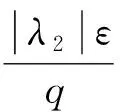



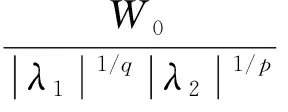

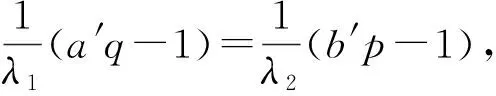



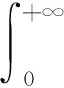

3 在算子理论中的应用