Frobenius扩张下的GC-平坦性

周绪杰, 赵志兵

(安徽大学 数学科学学院, 合肥 230601)

0 引 言

Frobenius扩张作为Frobenius代数的一种推广, 是一类被广泛关注的环扩张, 其基本例子是群代数为其指数有限的子群代数上的一个Frobenius扩张. 目前, 同调不变性质的保持性是Frobenius扩张理论的热门课题[1-3].

对于环扩张A/S, 有一个限制函子R=HomA(SAA,-)(≅-⊗AAS): Mod-A→Mod-S将MA作用为MS.在相反方向有两个函子T=-⊗SAA: Mod-S→Mod-A和H=HomS(AAS,-): Mod-S→Mod-A.易验证, (T,R)和(R,H)都是伴随对.

定义1[4]如果下列等价条件之一成立, 则环扩张A/S称为Frobenius扩张：

半对偶模[5-6]是对偶模的一种推广, 最初要求环总是Noether的. 相对于一个半对偶模, Golod[7]定义了GC-维数, 其统一了经典的投射维数和Gorenstein投射维数. 文献[8]去掉了“Noether”的条件, 考虑一般的交换环上相对于半对偶模的GC-维数, 包括GC-投射、 内射和平坦维数.

定义2[8]如果一个S-模C满足下列条件, 则该S-模C称为半对偶模:

显然, 正则模S本身就是一个半对偶模, 若存在对偶模, 则其是一个半对偶模.由文献[9]中命题2.3可知, 半对偶模在环的Frobenius扩张下是保持的.

命题1[9]设A/S是环的Frobenius扩张, 若C是半对偶S-模, 则C⊗SA是半对偶A-模.

一个模的GC-平坦性在环的优越扩张下是保持的[9].优越扩张一定是Frobenius扩张, 而半对偶模在Frobenius扩张下是保持的, 因此本文考虑GC-平坦模在Frobenius扩张下的保持性, 下面给出GC-平坦模的定义.

定义3设C是一个半对偶S-模.一个S-模M称为GC-平坦模, 是指存在S-模的正合序列

F∶=…→F1→F0→C⊗SF0→C⊗SF1→…,

(1)

使得M≅Coker(F1→F0), 且对于每个内射S-模I, 复形F⊗SHomS(C,I) 都是正合的, 其中Fi和Fi均是平坦模.此外, 上述正合序列F称为M的完全FC-分解.

注1若C=S, 则GC-平坦模与经典的Gorenstein平坦模一致.

如果一个S-模类X包含每个投射S-模, 且对每个S-模正合序列0→X′→X→X″→0, 若X″∈X, 则有X′∈X当且仅当X∈X, 则称该S-模类X是投射预解类.对所有GC-平坦模构成的类, 由文献[9]中命题2.9有如下命题.

命题2若S是凝聚环,C是一个半对偶S-模, 则GC-平坦S-模类是投射预解类, 且对任意直和与直和项封闭.

由文献[10]中引理3.12可得如下命题.

命题3设M是一个S-模, 如果有下列两个正合序列:

本文主要考虑模的GC-平坦性和GC-平坦维数在环的Frobenius扩张下的保持性.若A/S是Frobenius扩张且基环S是凝聚环, 首先证明对于任意的A-模M,MA是GC⊗SA-平坦模当且仅当M作为S-模是GC-平坦模.其次, 证明GC-平坦维数沿着环的Frobenius扩张是不变的, 即对于一个A-模M, 有GC-fdS(M)=GC⊗SA-fdA(M).这些结果均推广或强化了经典(Gorenstein)同调维数的一些相关结论.

1 GC-平坦模

下面讨论GC-平坦模在Frobenius扩张下的保持性.首先, 根据定义3有如下的GC-平坦模特征性质.

命题4一个S-模M是GC-平坦模当且仅当M满足下列条件：

定理1设A/S是Frobenius扩张,M是任意S-模.若S是凝聚环, 则M是GC-平坦S-模当且仅当M⊗SA是GC⊗SA-平坦A-模.

证明： 必要性.由文献[9]中命题4.8直接可得.

充分性.假设M⊗SA是GC⊗SA-平坦A-模.断言M⊗SA作为S-模是GC-平坦模.事实上,SA是有限生成投射模, 对任意内射S-模I, 由文献[11]中定理3.2.9和引理3.2.4可知,I⊗SA≅HomS(AAS,IS)是内射A-模, HomA(C⊗SA,I⊗SA)≅HomS(C,I)⊗SA.故对∀i≥1, 有

其中P·是M⊗SA的删项投射分解.

此外, 有A-模正合序列

Z∶=0→M⊗SA→(C⊗SA)⊗AF0→(C⊗SA)⊗AF1→…,

其中每个Fi都是平坦A-模, 使得对任意的内射A-模I, 复形Z⊗AHomA(C⊗SA,I)正合.注意到Z作为S-模序列也正合, 且对任意的内射S-模I, 有

Z⊗SHomS(C,I)≅(Z⊗AA)⊗SHomS(C,I)≅Z⊗A(HomS(C,I)⊗SA)≅Z⊗AHomA(C⊗SA,I⊗SA)

正合.所以由命题4知,M⊗SAS是GC-平坦模.因为MS是M⊗SAS的直和项, 故由命题2知,M是GC-平坦S-模.证毕.

由定理1充分性的证明过程可得如下推论.

推论1设A/S是Frobenius扩张,M是任意A-模.若M是GC ⊗SA-平坦模, 则M作为S-模是GC-平坦模.

由文献[12]中命题2.15的证明知,M是GC-平坦S-模当且仅当HomS(M,E)是GC-内射S-模, 其中E是任意内射S-模.对偶于文献[8]中推论3.8, 用文献[13]中命题3.8的证明方法, 有以下结论.

定理2设A/S是Frobenius扩张,M是任意A-模.若S是凝聚环, 则M是GC ⊗SA-平坦A-模当且仅当M作为S-模是GC-平坦模.

证明： 必要性.由推论1可得.

(3)

其中F0是平坦A-模,L0是GC⊗SA-平坦A-模.由推论1知,M⊗SA和L0作为S-模都是GC-平坦模.故由命题2知,C⊗SF0作为S-模也是GC-平坦模.

此外, 有映射i:MA→HomS(AAS,MS)(≅M⊗SAA),i(m)(a)=ma, 其中m∈M,a∈A.易验证i是A-模单同态, 且将i限制为S-模同态时是可裂的.令Q0=Coker(fi), 则有A-模短正合列:

(4)

f⊗SHomS(C,I): (M⊗SA)⊗SHomS(C,I) →(C⊗SF0)⊗SHomS(C,I).

(5)

再令N≅Coker(i), 则有A-模短正合列:

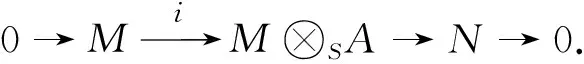
(6)

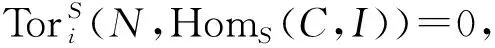
i⊗SHomS(C,I):M⊗SHomS(C,I)→(M⊗SA)⊗SHomS(C,I).

(7)

因此, 由式(5)和式(7)有S-模短正合列：

0→M⊗SHomS(C,I)→(C⊗SF0)⊗SHomS(C,I)→Q0⊗SHomS(C,I)→0,

对Q0重复上述过程, 可得到一个在函子-⊗AHomA(C⊗SA,I)作用下保持正合性的短正合列:

0→Q0→C⊗SF1→Q1→0,

其中F1是平坦A-模,Q1作为S-模是GC-平坦模.归纳地, 可以构造出一个A-模正合序列:

Z∶=0→M→C⊗SF0→C⊗SF1→…,

其中每个Fi是平坦A-模, 且对任意内射A-模I, 复形Z⊗AHomA(C⊗SA,I)正合.证毕.

设C和D分别是Mod-S的两个子范畴.一个函子F: C→D称为Frobenius函子是指存在另一个函子G: D→C, 使得(F,G)和(G,F)都是伴随对[14].根据定义1可知, -⊗SAA≅HomR(AAS,-)是由Frobenius双模AAS诱导的一个Frobenius函子.用GFC(S)表示所有GC-平坦S-模构成的Mod-S的全子范畴, 则有如下推论.

推论2设A/S是一个Frobenius扩张, 则Frobenius双模AAS诱导了一个从GFC(S)到GFC⊗SA(A)的Frobenius函子.

证明： 根据假设,T(=-⊗SAA)≅H(=HomS(AAS,-)): Mod-S→Mod-A是同时以限制函子R为左和右伴随的Frobenius函子.利用定理1和定理2, 分别有T|GFC(S)⊆GFC⊗SA(A)和R|GFC⊗SA(A)⊆GFC(S), 从而T是从GFC(S)到GFC⊗SA(A)的一个Frobenius函子.证毕.

2 GC-平坦维数

下面讨论GC-平坦维数在Frobenius扩张下的保持性.类似于经典同调维数的定义, 定义模的GC-平坦维数如下.

定义4设M是S-模, 定义M的GC-平坦维数GC-fdS(M)为M的GC-平坦分解的最短长度, 即

GC-fdS(M)=inf{n|∃GC-平坦分解0→Fn→…→F1→F0→M→0},

其中n是非负整数.如果M没有有限长度的GC-平坦分解, 则GC-fdS(M)=∞.

记GC-glfd(S)=sup{GC-fdS(M)|M是任意S-模}, 称为环S的整体GC-平坦维数.

定理3设A/S是Frobenius扩张, 且S是凝聚环, 则对于任意A-模M(M自然是一个S-模), 有GC-fdS(M)=GC⊗SA-fdA(M).

证明： 不妨设GC⊗SA-fdA(M)=n<∞, 则M有长为n的GC⊗SA-平坦分解.由定理2可知, 任意GC⊗SA-平坦A-模作为基环S上的模是GC-平坦S-模, 因此GC-fdS(M)≤n=GC⊗SA-fdA(M).

下证GC⊗SA-fdA(M)≤GC-fdS(M).设GC-fdS(M)=m<∞, 则有S-模正合序列:

0→Fm→Fm-1→…F1→F0→M→0,

(8)

其中Fi是GC-平坦S-模.对A-模M, 有A-模正合序列:

(9)

定理3表明, 相对于半对偶模的GC-平坦维数在环的Frobenius扩张下是保持的.

定理4设A/S是Frobenius扩张,S是凝聚环, 则对于任意S-模M, 有

GC-fdS(M)=GC⊗SA-fdA(M⊗SA).

证明： 利用定理1, 类似于定理3的证明方法即可证结论.

由定理3和定理4可得如下推论.

推论3设A/S是Frobenius扩张,S是凝聚环, 则GC-glfd(S)=GC⊗SA-glfd(A).

推论4设A/S是Frobenius扩张,S是凝聚环, 则有下列结论：

1) 对任意的A-模M, GfdS(M)=GfdA(M)； 2) 对任意的S-模M, GfdS(M)=GfdA(M⊗SA)； 3)r.Gglfd(S)=r.Gglfd(A), 其中r.Gglfd(S)表示环S的右整体Gorenstein平坦维数.

设C=S, 则推论4是文献[1]中定理3.7对应的结果.事实上, 本文去掉了文献[1]中定理3.7的可分条件.

注2根据定理2和定理3的证明可知, 推论3和推论4中的S和A可以不交换.