具有细胞内时滞的耦合传染病模型

王 颖, 王灵芝

(陕西师范大学 数学与统计学院, 西安 710119)

0 引 言

研究表明, 在宿主细胞中病毒感染主要有两种途径[1-4]： 病毒感染细胞(间接传播)和细胞间感染(直接传播). 事实上, 细胞间感染比病毒感染细胞更有效[5]. 细胞被病毒感染后, 存在一个较短的细胞内潜伏期, 目前数学上有两种方法模拟该潜伏期阶段： 通过一类显式的潜伏感染细胞[6-7]或通过一个时间延迟[2,4].

基于文献[2,4,8]的工作, 本文考虑含易感细胞的Logistic增长项、 感染期间的时滞和时滞阶段未成熟的已感染细胞死亡率几个因素的病毒感染模型, 模型可描述为如下形式的时滞微分方程：

(1)

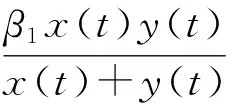
本文首先证明系统解的非负性和一致有界性, 确定可行域； 其次, 通过分析特征方程利用Lyapunov-LaSalle不变性原理[10]证明无感染平衡点P0的全局渐近稳定性, 并通过分析病毒感染平衡点P*的稳定性给出Hopf分岔的存在条件； 最后利用MATLAB软件进行数值模拟以验证所得结论.

1 适定性与可行平衡点

为分析当τ≥0时平衡点的稳定性和系统(1)的动力学行为, 需要考虑一个合适的相空间和可行域.当τ>0时, 记C∶=([-τ,0],), 对于任意的φ∈C, 定义范数为从区间[-τ,0]映射到的连续函数全体构成的Banach空间.记C+∶=([-τ,0],+)为C的非负锥.当t=0时, 系统(1)的初始条件为

φ∈X∶=+×C+×C+.

(2)

定理1在初始条件(2)下, 系统(1)的解具有非负性和一致有界性.

证明： 首先利用反证法证明解的非负性.

假设t1>0,t1是第一次使x(t)=0的时刻, 即x(t1)=0.由系统(1)的第一个方程可知x′(t1)=λ>0, 故存在ε>0, 使得当t∈(t1-ε,t1)时, 有x(t)<0.这与当t∈[0,t1)时,x(t)>0矛盾, 故x(t)≥0.假设t2>0,t2是第一次使y(t)=0的时刻, 即y(t2)=0, 则∀t∈[0,t2), 有y(t)>0.由系统(1)的第二个方程得y′(t2)≥β2e-μτx(t2-τ)z(t2-τ), 由系统(1)的第三个方程得z′(t)=py(t)-δz(t).而在[0,t2)上,y(t)>0, 故∀t∈[0,t2),z′(t)≥-δz(t), 即∀t∈[0,t2),z(t)≥z(0)e-δt2>0; 从而在[0,t2) 上,z(t)>0, 故

y′(t2)≥β2e-μτx(t2-τ)z(t2-τ)>0,

即y′(t2)>0.于是存在ε>0, 使得当t∈(t2-ε,t2)时, 有y(t)<0.这与当t∈[0,t2)时,y(t)>0矛盾, 故y(t)≥0.而由系统(1)的第三个方程有

因此,x(t),y(t),z(t)在+×C+×C+上非负.

其次证明解的一致有界性.

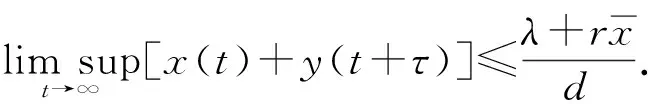
本文在如下有界可行域内分析系统(1)的动力学行为：

其中区域Γ相对于系统(1)是正不变的且系统(1)是适定的.

2 无感染平衡点的全局稳定性

系统(1)在P0处的特征方程[12]为

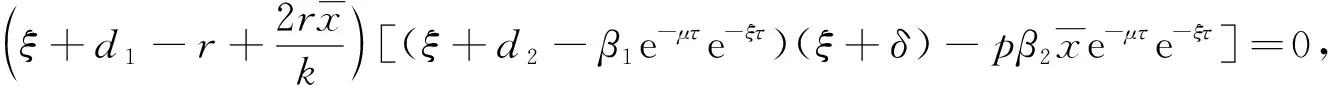
(4)

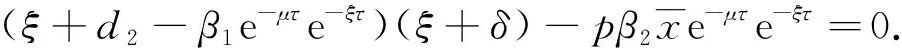
(5)

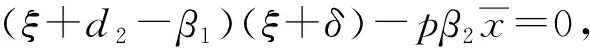
故0不是特征方程(4)的根.下面考虑当τ>0时式(5)根的分布.假设ξ=iω(ω>0)是式(5)的根, 将iω代入式(5)并分离实虚部, 有

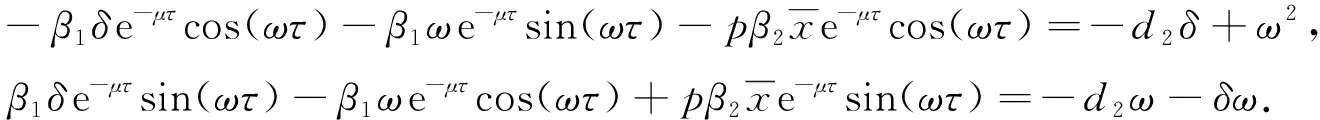
(6)

由式(6)可得

因为R0<1, 所以式(6)的根无正解, 即式(5)没有纯虚根.故方程(5)对∀τ>0无纯虚根, 即方程的根不能穿过虚轴, 并在τ≥0的情形下保持在虚轴左侧.因此若R0<1, 则特征方程(4)的所有根均有负实部, 从而无感染平衡点P0局部渐近稳定.下面利用Lyapunov泛函证明当R0≤1时,P0全局渐近稳定.

定理2若R0≤1, 则无感染平衡点P0全局渐近稳定.

证明： 考虑如下Lyapunov泛函：

(7)

其中xt(θ)=x(t+θ),yt(θ)=y(t+θ),zt(θ)=z(t+θ),θ∈[-τ,0].计算L沿系统(1)的时间导数：

(8)

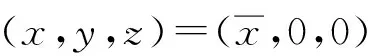
3 病毒感染平衡点的稳定性和Hopf分岔

系统(1)在P*处的特征方程[12]为

ξ3+A2ξ2+A1ξ+A0+(B2ξ2+B1ξ+B0)e-ξτ=0,

(9)

其中,

当τ=0时, 特征方程(9)为

ξ3+(A2+B2)ξ2+(A1+B1)ξ+A0+B0=0,

(10)

其中,

此时平衡点需满足以下条件：

故有

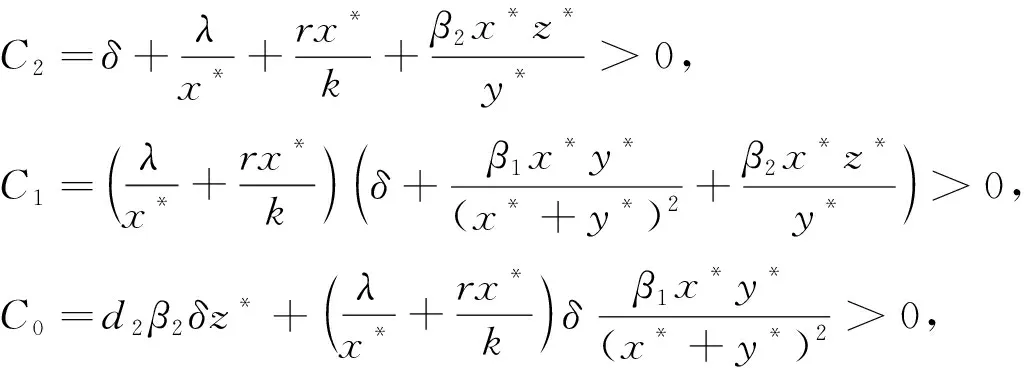
(11)

及

由Routh-Hurwitz准则可知, 当τ=0时, 方程(10)的所有根均具有负实部当且仅当满足下列条件：

(H0)C2C1-C0>0.

从而下列结论成立.

引理1若R0>1且(H0)成立, 则病毒感染平衡点P*当τ=0时渐近稳定.

此外, 对任意的τ≥0, 均有

故0不是特征方程(9)的根.下面考虑当τ>0时, 特征方程(9)纯虚根的存在性.假设u=iω(ω>0)是特征方程(9)的一个根, 将iω代入方程(9)并分离实部和虚部, 得

将方程(12),(13)先平方再相加, 可得

F(ω,τ)=ω6+C2(τ)ω4+C1(τ)ω2+C0(τ)=0,

(14)

其中

从而iω(ω>0)是方程(9)纯虚根的必要条件是ω为F(ω,τ)=0的正根.多项式方程F可以写成如下形式：F(ω,τ)=h(ω2,τ), 其中h是一个三次多项式：

h(v,τ)∶=v3+C2(τ)v2+C1(τ)v+C0(τ).

(15)

由于P*=(x*,y*,z*)满足系统(1), 因此可重写上述表达式为

又因为

(16)

并且h(v,τ)在v-处取得极大值, 在v+处取得极小值,

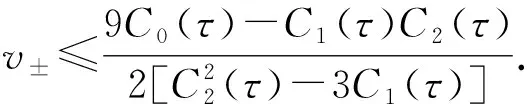
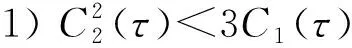
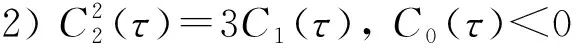
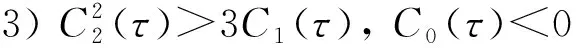
故Hopf分岔存在的充分条件是引理2中条件1)～4)成立.为方便, 记使得引理2中条件1)～4)成立的[0,τmax)的子集为I.当引理2中条件1)～4)成立时, 对于τ∈I, 存在一个ω=ω(τ)>0, 使得F(ω(τ),τ)=0.若iω(τ*)是特征方程(9)的根, 则ω(τ*)必须满足

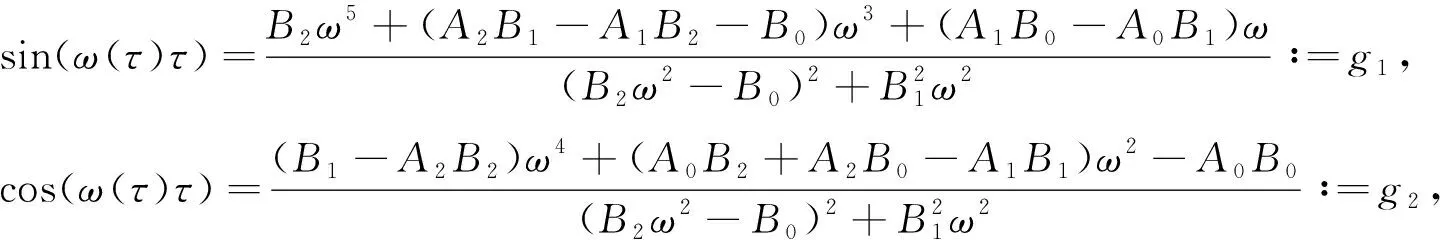
(17)

因为当τ∈I时,F(ω(τ),τ)=0成立.故θ(τ)存在且唯一.

由ω(τ)τ=θ(τ)+2nπ, 可知iω*(ω*=ω(τ*)>0)是特征方程(9)的纯虚根当且仅当τ*为函数Sn的零解, 函数Sn定义为

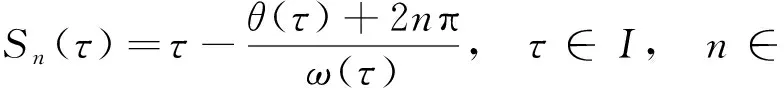
(18)

下面介绍Beretta等[14]关于判断系数依赖时滞的超越方程发生稳定性开关的几何准则.

定理3假设ω(τ)是F(ω(τ),τ)=0在I上的一个正实根.如果存在τ*∈I满足Sn(τ*)=0(n∈0), 则当τ=τ*时, 特征方程(9)具有一对共轭纯虚根ξ(τ*)=±iω(τ*).进一步, 若Sign Reξ′(τ*)>0, 则在复平面上这对纯虚根对应的共轭复根随着τ的变化从左至右穿过虚轴； 反之, 若Sign Reξ′(τ*)<0, 则它们从右至左穿越虚轴, 其中

证明： 由文献[14]可知,

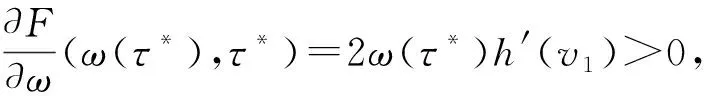
由式(18)可知Sn(0)<0, 且对所有的τ∈I,Sn(τ)>Sn+1(τ), 其中n∈0.因此, 如果S0在I中没有零解, 则对所有的n∈0, 函数Sn在I中都没有零解.另一方面, 若存在n∈0, 使得Sn(τ)有正根, 记为不失一般性, 假设

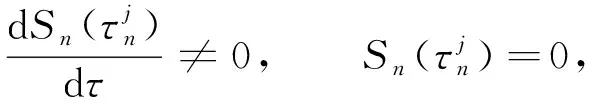
(19)

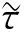
综合上述分析, 利用泛函微分方程的Hopf分岔定理, 可得关于Hopf分岔的存在性定理：

定理4对于系统(1), 如果R0>1且引理2中条件1)～4)成立, 则有下列结论：

(i) 如果函数S0(τ)在I中没有零点, 则对所有的0≤τ<τmax, 病毒感染平衡点P*均是渐近稳定的；

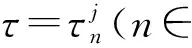
4 数值模拟

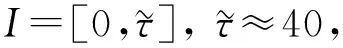
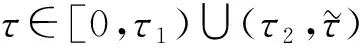
图1 函数S0和S1在区间τ∈I上的图像Fig.1 Images of functions S0 and S1 on τ∈I

图2 系统(1)的分岔图Fig.2 Bifurcation diagram of system (1)

由Hopf分岔的讨论可知, 系统(1)发生Hopf分岔的τ区间为(τ1,τ2).选取时滞参数τ=0.01∈[0,τ1), 此时系统(1)的病毒感染平衡点P*渐近稳定, 如图3所示.选取时滞参数τ=30∈(τ1,τ2), 此时系统(1)的病毒感染平衡点P*不稳定, 如图4所示.模拟结果与定理4的结论相符.

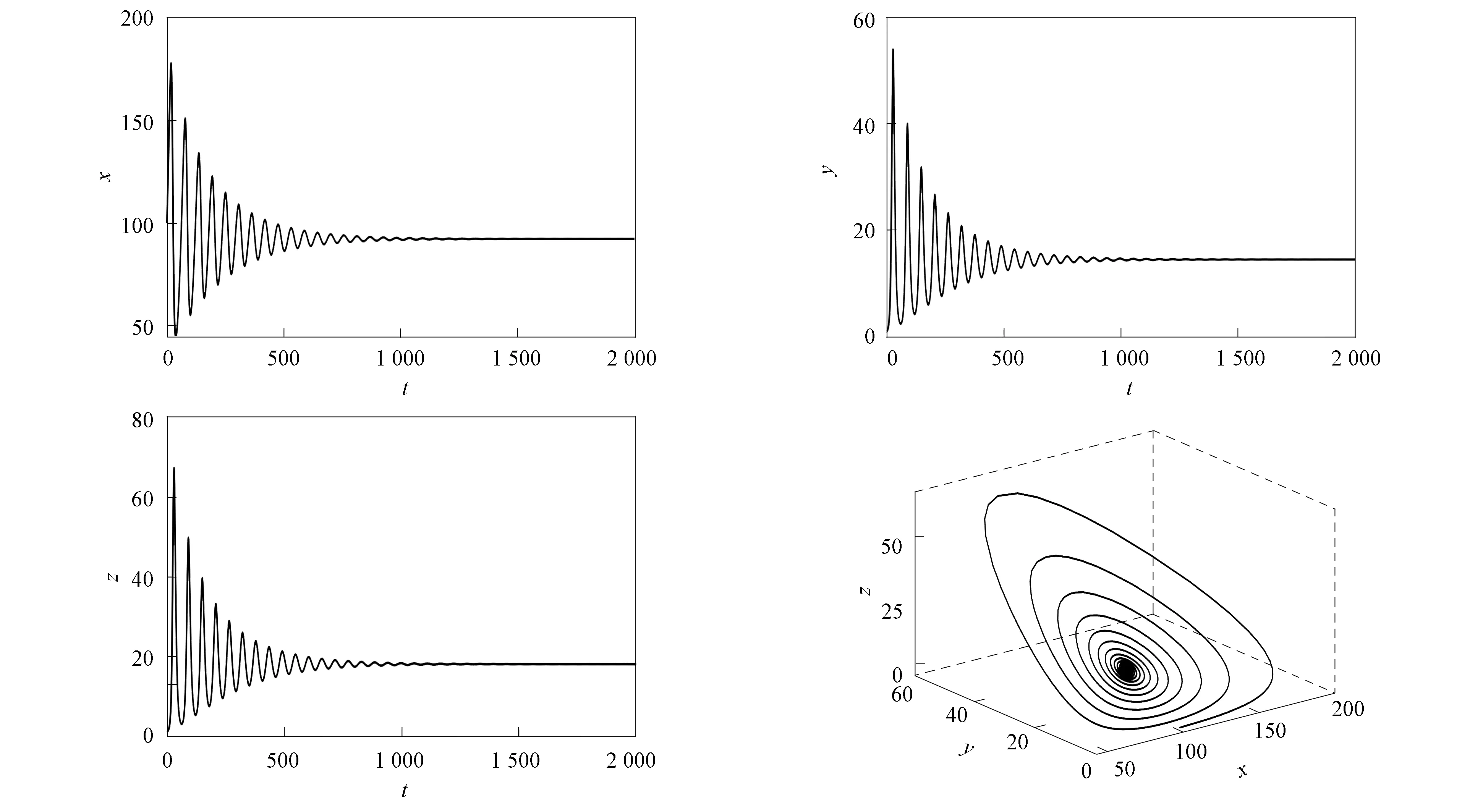
图3 当τ=0.01∈[0,τ1)时, P*渐近稳定Fig.3 P* is asymptotically stable when τ=0.01∈[0,τ1)

图4 当τ=30∈(τ1,τ2)时, P*不稳定Fig.4 P* is instability when τ=30∈(τ1,τ2)

综上所述, 本文研究了一类具有Logistic增长的时滞耦合模型.首先, 通过公式推导得到: 当R0≤1时, 无感染平衡点P0是全局渐近稳定的； 其次, 给出了病毒感染平衡点P*局部渐近稳定的充分条件以及系统(1)发生Hopf分岔的充分条件; 最后, 采用MATLAB软件数值模拟验证了所得结果的正确性.