函数的概念与性质复习导航

张明同

(山东省寿光市教育科学研究中心)

函数的概念与性质是高中数学最基本的知识,这些知识是解决整个高中数学问题的“第一步”,如果没有这“第一步”的知识,整个数学的学习都会步履维艰.因此,牢固掌握函数的概念与性质是数学解题的基石,是高考取胜的法宝,本文将在“函数”这一大概念视域下结合例题引导读者认真复习这一部分内容.

1 函数有关概念及其应用

1.1 函数的定义

1.2 函数的定义域

1.3 函数的最值

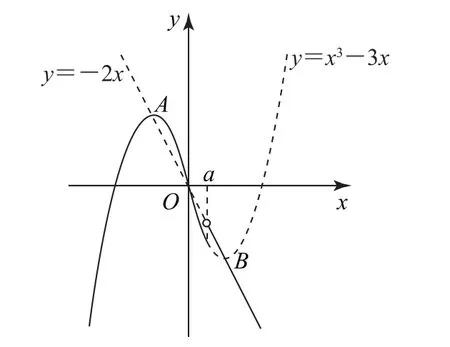
图1

1.4 求函数的解析式

1.5 分段函数问题

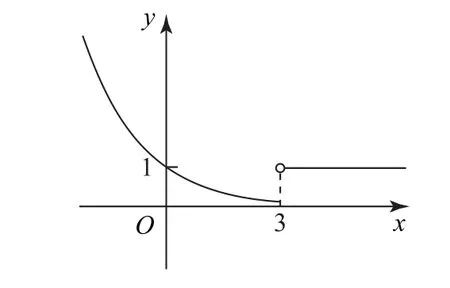
图2

2 函数图像综合问题

2.1 由解析式确定图像

2.2 图像的变换

例9 (1)已知函数f(1－x)的图像如图3所示,则y＝|f(x＋2)|的图像大致是( ).

图3

(2)设函数f(x)的定义域为R,且|f(x)|是偶函数,则( ).

A.f(x)是偶函数

B.f(x)是奇函数

C.|f(x－1)|图像的对称轴是x＝1

D.|f(x)＋1|图像的对称中心是(0,1)

(1)将f(1－x)的图像左移1 个单位得f(－x)的图像,再关于y轴对称可得f(x)的图像,再左移2个单位得到f(x＋2)的图像,再将f(x＋2)的图像在x轴下方的部分沿x轴翻折上去,故选A.

(2)若f(x)＝x,则可判断A 不正确.同样地,若f(x)＝x2,则可判断B 不正确.若f(x)＝x,则|f(x)＋1|＝|x＋1|图像关于x＝－1对称,所以D不正确.函数f(x)的图像右移1个单位,可得f(x－1)的图像,又因为函数|f(x)|是偶函数,关于y轴对称,所以函数|f(x－1)|关于直线x＝1对称.故选C.

对于函数图像的变换问题,应充分利用特殊点和函数的单调性、对称性、周期性等性质及平移、翻折等知识进行综合分析与判断.

2.3 实际情境中的函数图像

例10 如图4所示,圆A的半径为1 m,圆心A在y轴上,将圆A沿y轴匀速向上平移,在t＝0时,圆A第一次经过原点O,平移的速度为1m·s－1.记圆A位于x轴上方的圆弧的长为x,令y＝cosx,则y与时间t(0≤t≤1,单位:s)的函数y＝f(t)的图像可以是( ).

图4

2.4 利用图像研究不等式或方程

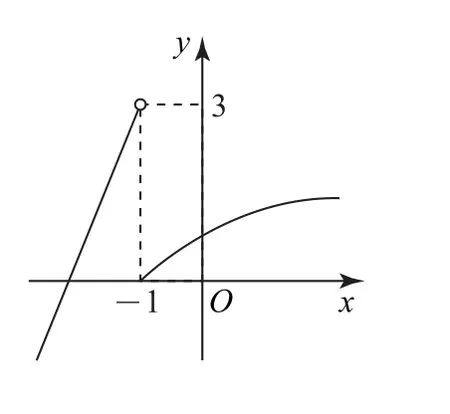
图5

图6

3 函数性质的综合应用

3.1 单调性与奇偶性相结合

3.2 周期性与奇偶性相结合

3.3 由奇偶性确定参数的取值(或范围)