强基计划数学备考系列讲座(6)——集合与函数(上)

王雪芹 王慧兴

(1.北京师范大学第二附属中学 2.清华大学附属中学)

高校强基计划校考试题与高考试题突出互补性,本文基于这种互补性构建“集合与函数”学习辅导.

1 知识与技能

1.1 集合

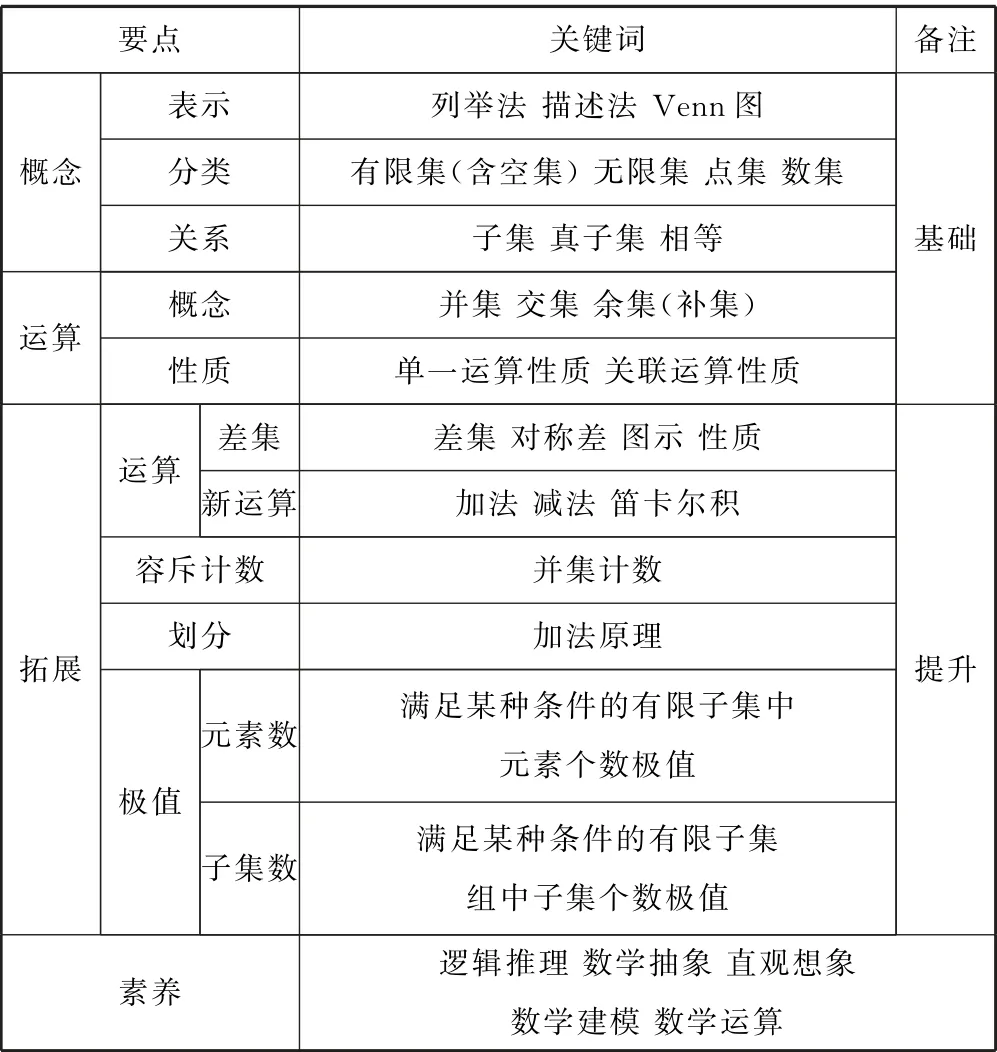
表1

1.2 常用逻辑

表2

1.3 函数

表3

2 要点解析

2.1 反证法

准确提出反证假设,由之出发,经逻辑推理,揭示出矛盾,得出反证假设不成立,从而肯定欲证命题成立.反证法是间接论证命题的一种方法,其本质是证明“原命题的否定”不成立,或论证其“逆否命题”成立；提出反证假设,融入已知,相当于增加一个条件,再进行推理,目标是构建矛盾.

2.2 集合运算关联性质

设U为全集,集合A,B,C⊆U,记集合X(X⊆U)的补集为ˉX＝∁UX.

2.3 差集与对称差

(1)差集:AB＝{x|x∈A,x∉B}.

(2)对称差:AΔB＝(AB)∪(BA)＝(A∪B)(A∩B).

(3)A∩B＝A(AB)；通常A(AB)⊆B,特别地,当B⊆A时,有A(AB)＝B.

(4)记有限集合X的元素个数为|X|,则对有限集合A,B,有|A∪B|＝|A|＋|B|－|A∩B|,特别地,当A∩B＝∅时,有

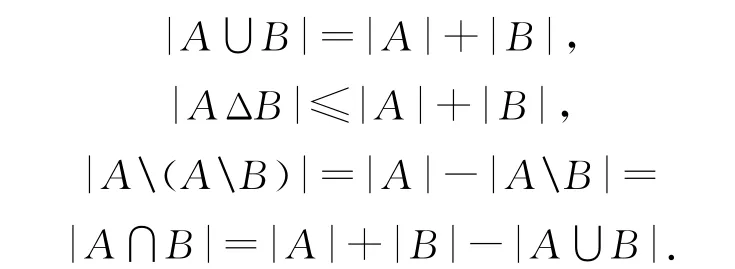
(5)若非空有限集合A,B满足|A∩B|＝1,则|A|＋|B|≥3.

2.4 集合之间定义加法、减法、乘法等新运算

(1)加法:A＋B＝{a＋b|a∈A,b∈B}.

(2)减法:A－B＝{a－b|a∈A,b∈B}.

(3)数乘:kA＝{ka|a∈A}.

(4)乘法:A·B＝{ab|a∈A,b∈B}.

(5)笛卡尔积:A×B＝{(a,b)|a∈A,b∈B},坐标平面点集R2＝{(x,y)|x,y∈R}.

2.5 集合划分与加法原理

(1)集合划分:如果集合S的一组两两交集都是空集的非空子集A1,A2,…,An,满足A1∪A2∪…∪An＝S,则称子集组{A1,A2,…,An}构成集合S的一个n-划分；对任意一子集A⊆S,都有

A＝(A∩A1)∪(A∩A2)∪…∪(A∩An).

加法原理:对有限集合S的任意一n-划分{A1,A2,…,An},都有|S|＝|A1|＋|A2|＋…＋|An|.

(2)容斥计数原理:对任意一组有限子集A1,

2.6 子集极值

(3)子集极值有两类问题,其一是满足某种条件的子集中元素个数最多或最少的问题,其二是满足某种条件的子集组中子集个数最多或最少的问题.

2.7 函数图像

函数图像提供直观想象情境,函数y＝f(x)(x∈D)的图像是指点集Ff＝{(x,f(x))|x∈D}在坐标系中的可视化表现,通常是一条曲线,或一个点列.其基本特征:任意一垂直于x轴的直线至多与这条曲线有一个公共点,要把握各种典型函数的图像.

2.8 数形结合

基于图像建立不等式是不等式证明与多元最值探究的一项基本技能,也是学以致用的根本要求.例如,基于函数y＝sinx图像,可以建立如下不等式:

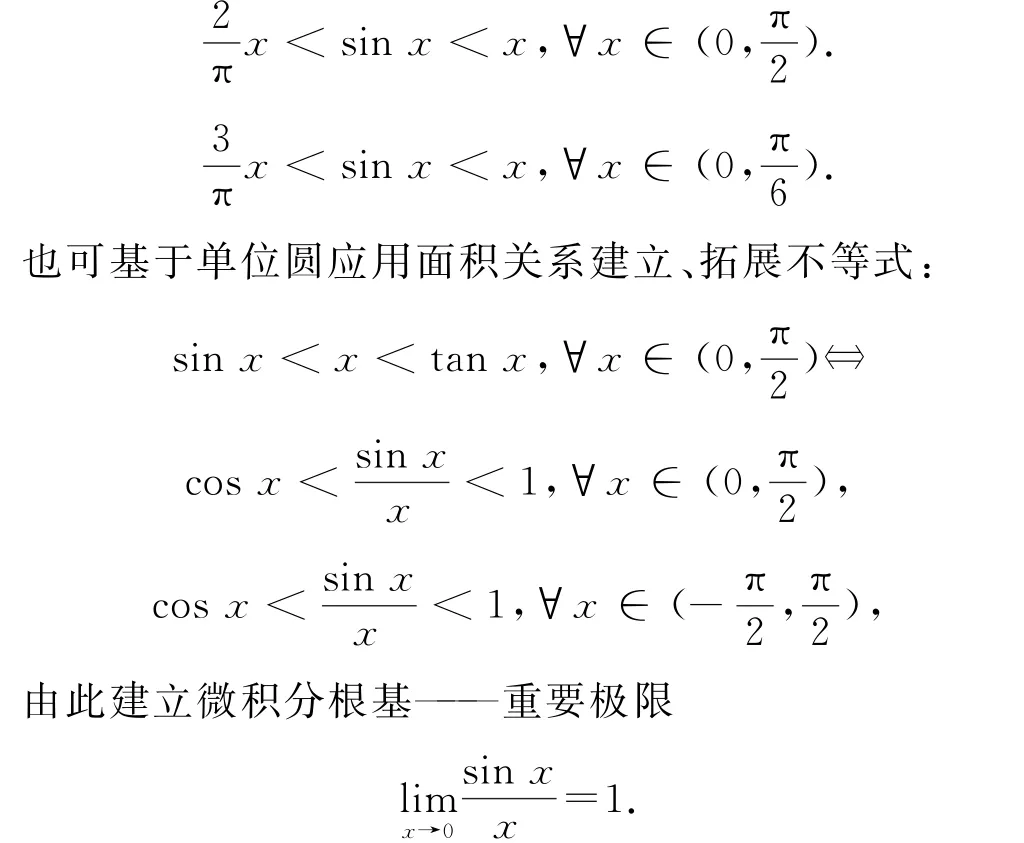
2.9 典型函数

我们在初等函数中提出典型函数概念,它由基本初等函数建构,分为两个层次,把不需要借助导数工具就能理解性质与作图的一些初等函数称为第一类典型函数,而把需要应用导函数才能分析性质与作图的一些初等函数称为第二类典型函数,第一类典型函数分为如下五条主线,如表4所示.

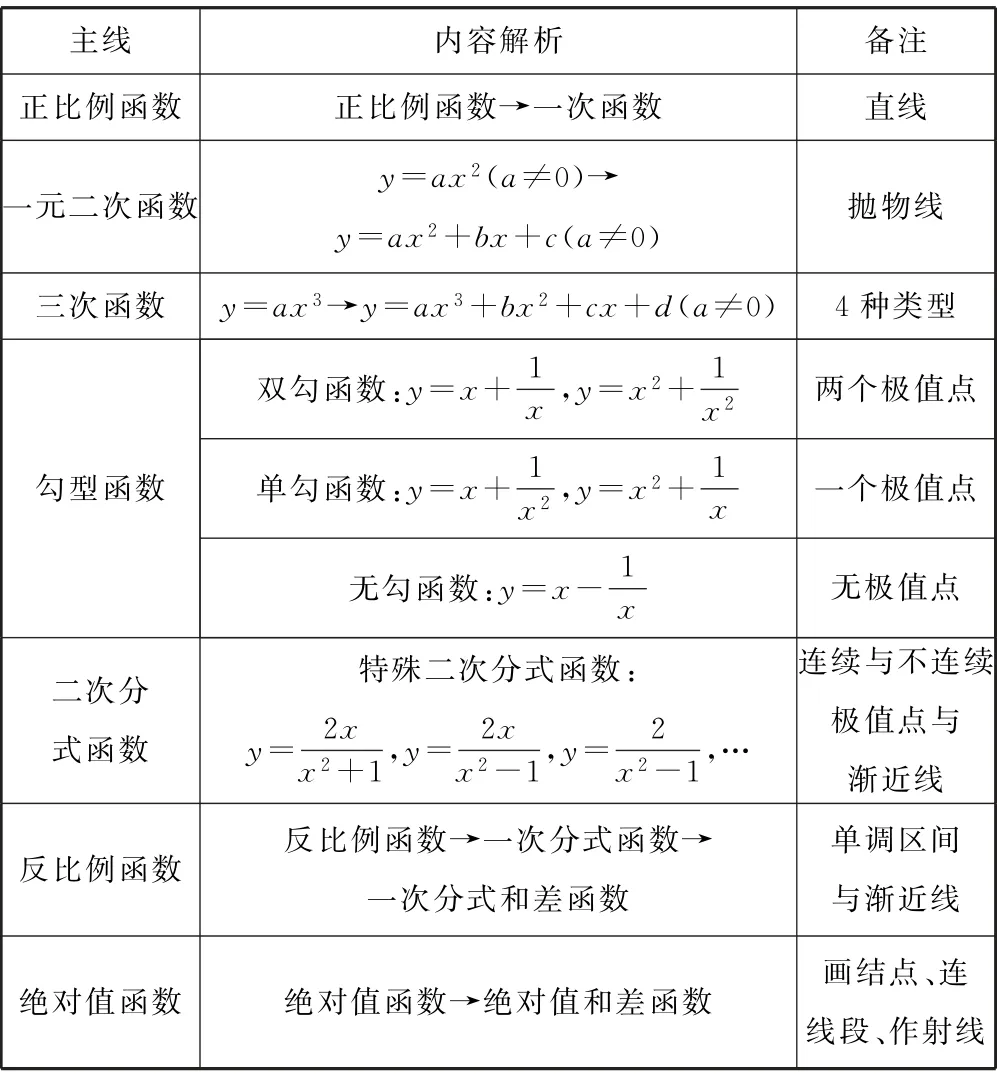
表4

2.10 映射抽象

设函数y＝f(x)(x∈D)的值域记作M,从定义域到值域上的映射f:D→M,当这个映射是双射时,就有逆映射f－1:M→D,由此定义反函数y＝f－1(x)(x∈M).

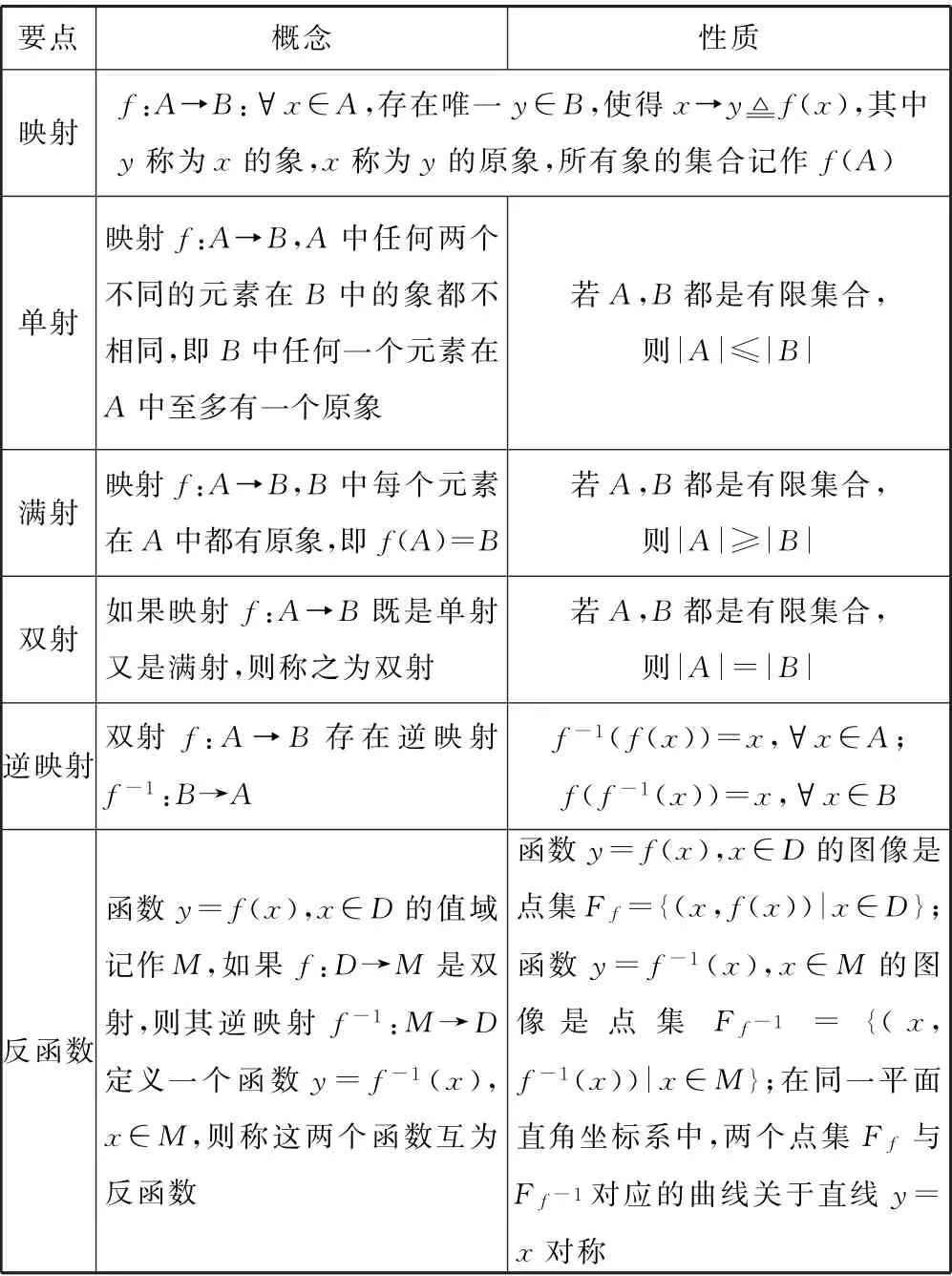
表5

2.11 复合与迭代

表6

2.12 函数方程

(1)函数方程及其解法

表7

(2)柯西方程

表8

要完整掌握柯西方程,从高校自主招生试题与强基计划校考出现过的函数方程题目来看,强基命题十分重视柯西方程这个基本模型.这不仅是因为函数方程是函数分析路径的顶端,即“基本初等函数→初等函数→抽象函数→函数方程→微积分方法→微分方程→……”,另一个重要原因是通过求解函数方程能深刻地培育学生逻辑推理、数学抽象、直观想象、数学运算、数据分析与数学建模等数学素养.因此,同学们要注重历练函数方程求解,尤其是柯西方程及其变式.

(3)柯西方程变式

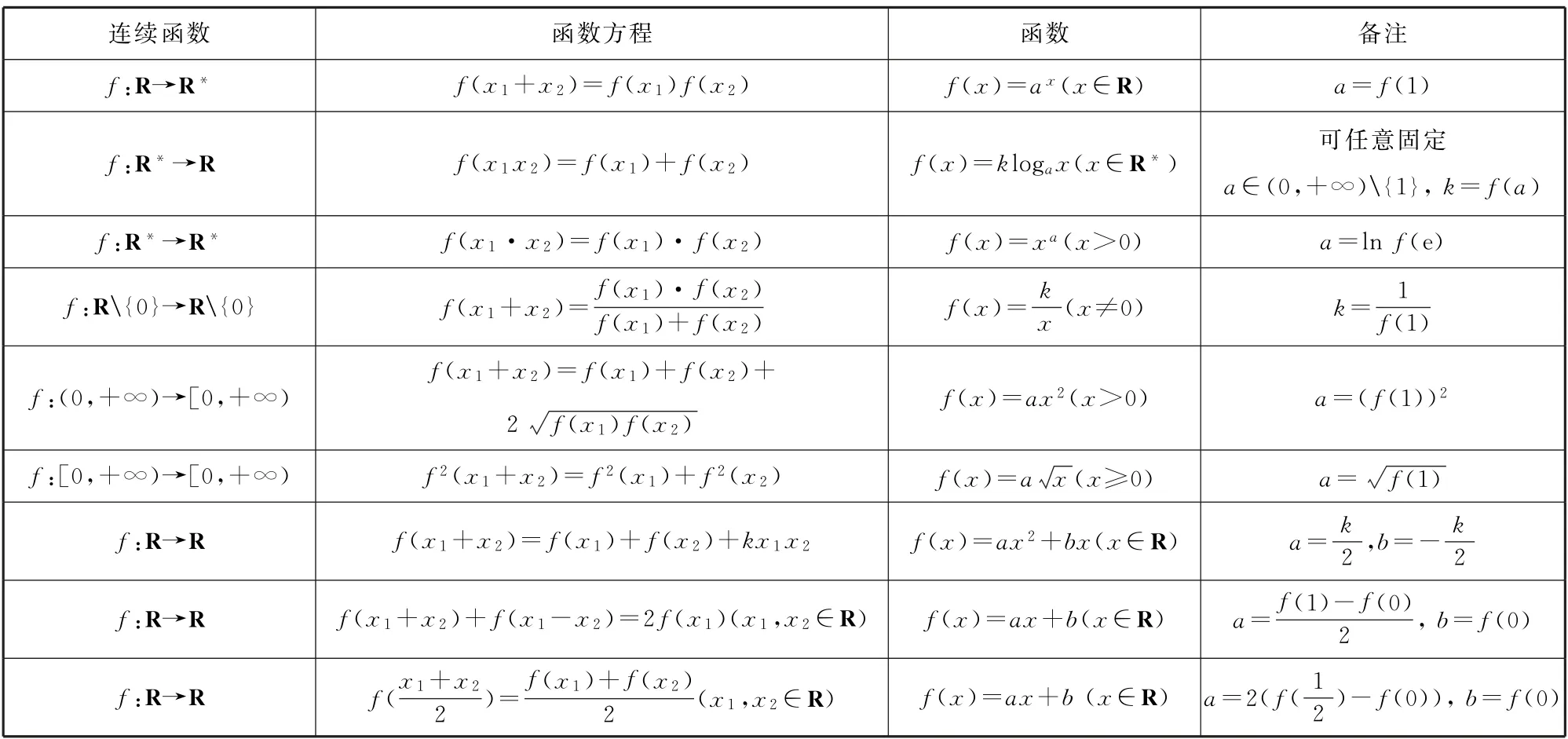
表9

3 典例精析

3.1 集合

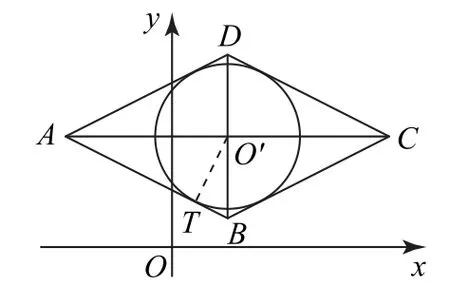
图1

3.2 逻辑用语

3.3 代数式灵活变形

代数式灵活变形既表现在恒等变形又表现在合理放缩,向着目标调结构.

例6 (清华大学)已知实数a,b满足a3＋b3＋3ab＝1,其中a＋b取值的集合为M,则( ).

A.M是单元素集

B.M为有限集,但不是单元素集

C.M是无限集,且有下界

D.M是无限集,且无下界

3.4特型方程求解

3.5 定义与三要素

函数的三要素是理解函数、分析函数的性质、论证函数问题的基础,在各种变式情境中都要准确理解函数三要素.

所以A⊗B＝AΔB＝(－ ∞,－3]∪[0,1)∪(3,＋∞).

3.6 映射与反函数

高校强基计划校考试题提示我们,对函数学习的要求务必上升到映射观点理解函数,清晰理解反函数概念及其双射基础,能够以互为逆映射理解对数恒等式与反三角恒等式,培育抽象素养.

因为f(x)＝3x－3－x是奇函数,所以f－1(x)也是奇函数,从而f－1(4)＋f－1(－4)＝0,故gmax(x)＋gmin(x)＝2.

3.7 函数分析路径

强基计划校考试题注重函数分析,取定一个较复杂的初等函数,以不定项选择题型引领学生分析其性质,试题表现函数分析基本路径是三要素→基本性质(对称、单调、周期)→凹凸性→数形结合,建立函数不等式等.

由①③可知,∀x∈R,都有f(x)＝f(1－x)＝－f(2a－1＋x)＝－f(2－2a－x)＝f(4a－2＋x),

故函数y＝f(x)是周期函数,周期T＝4a－2≠0,且

3.8 典型函数

强基计划校考命题十分注重以典型函数及其变式立意试题,既检测代数变形能力与数学直观,又检测函数分析方法.

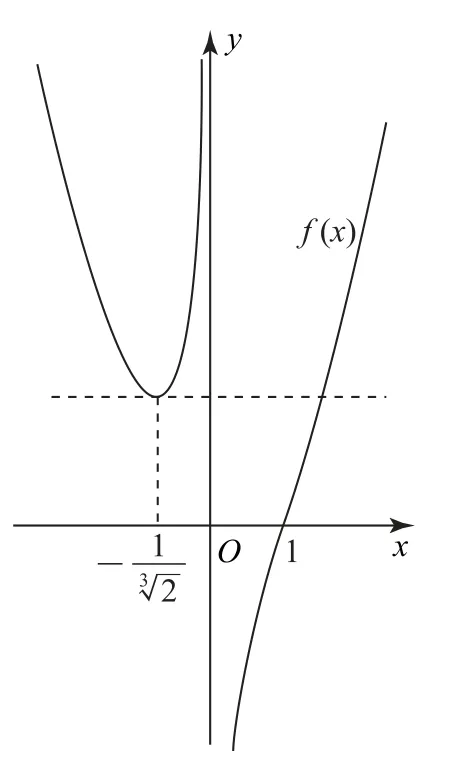
图2

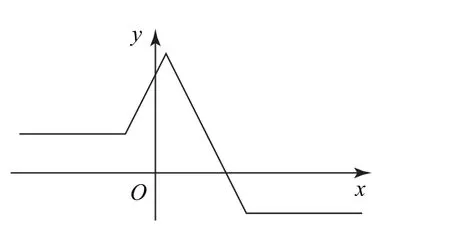
图3