追踪高考中的函数性质问题

李亚军

(河南省郑州市回民高级中学)

函数知识是高中的核心知识,也是高考试题的常考知识点之一.高考中不仅会考查常见的函数三要素,还会涉及函数的图像与性质、函数的应用、函数与方程等.下面以2021年的高考试题为例,追踪高考中的函数性质问题.

1 比较大小

2 函数的单调性

3 函数的图像识别

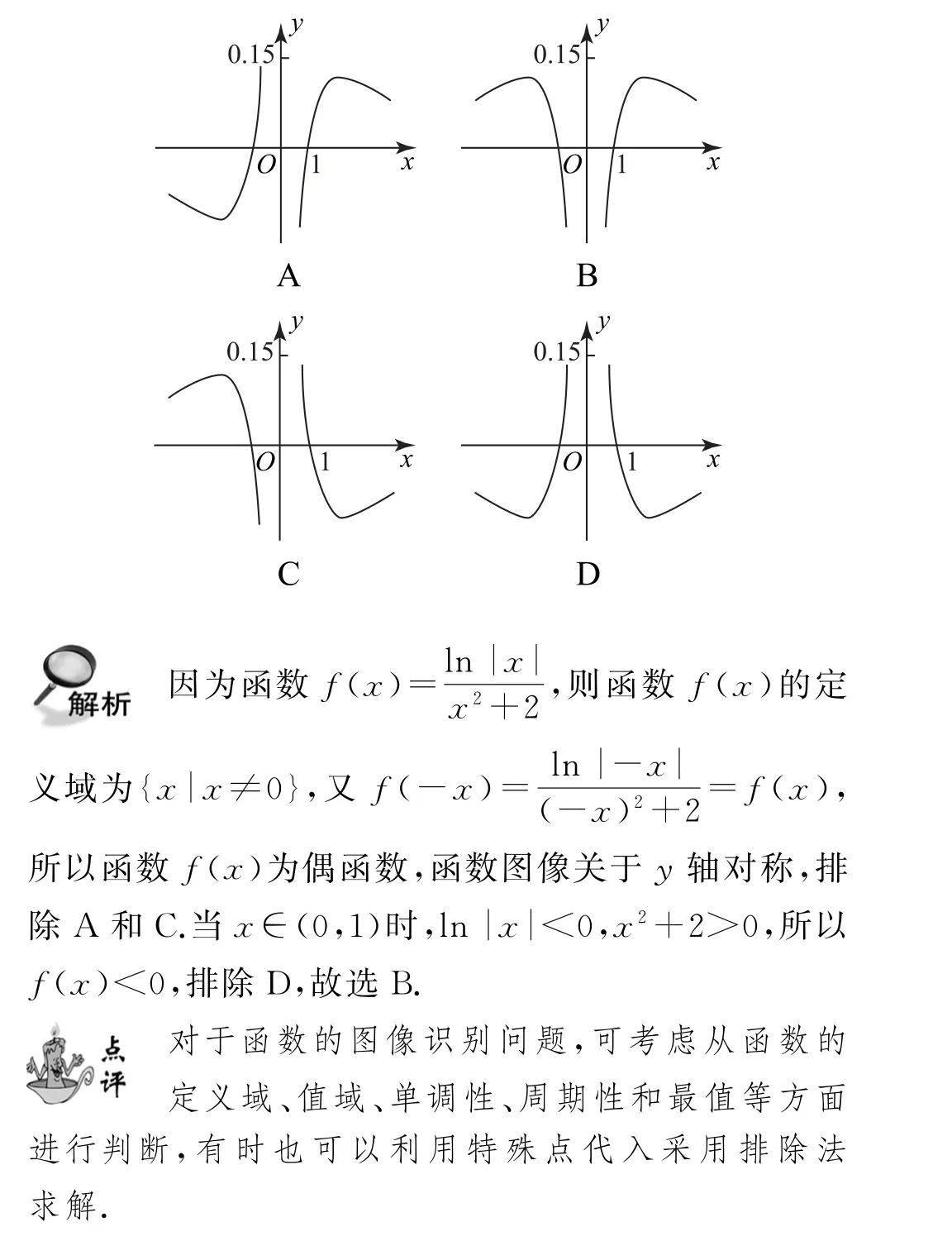
4 函数的奇偶性与周期性

例4 (2021新高考Ⅱ卷8)已知函数f(x)的定义域为R,且f(x＋2)为偶函数,f(2x＋1)为奇函数,则( ).

因为函数f(x＋2)为偶函数,则f(2＋x)＝f(2－x),可得f(x＋3)＝f(1－x).因为函数f(2x＋1)为奇函数,则f(1－2x)＝－f(2x＋1),所以f(1－x)＝－f(x＋1),所以

f(x＋3)＝－f(x＋1)＝f(x－1),

即f(x)＝f(x＋4),故函数f(x)是以4为周期的周期函数.因为函数f(2x＋1)为奇函数,则f(1)＝0,故f(－1)＝－f(1)＝0,故选B.

借助函数周期性解决求函数值或函数零点个数等问题是常考问题,在未明确给出周期的情况下,可先运用对称性与周期性的关系等确定周期,再运用函数的周期性找到解决问题的突破口.

5 函数的应用

6 函数零点

例6 (2021 年北京卷15)已知函数f(x)＝|lgx|－kx－2,给出下列四个结论:

故f(x)在(10－2,10－1)上至少有1个零点.又f(1)＝0,结合图像知,f(x)在(0,1]上有2个零点,即y＝|lgx|与y＝－2x＋2有2个不同的交点,故当直线过点(0,2)且与函数y＝|lgx|相切时,此时f(x)有1个零点,如直线l2,故②正确.

当k＜0时,函数y＝|lgx|与直线y＝kx＋2的图像至多有2个交点,故③不正确.

当k＞0且k足够小时,函数y＝|lgx|与直线y＝kx＋2的图像在(0,1)与(1＋∞)上分别有1个、2个交点,如直线l3,故④正确.

图1

本题考查了函数的零点与函数图像关系的应用,同时考查了命题真假性的判断、化归与转化、数形结合等思想方法的应用,难度较大.根据函数的性质正确画出函数y＝|lgx|与直线y＝kx＋2的图像是解决此题的关键.