长跨中间轴双悬臂转子轴流式引风机振动分析及治理

李卫军，何玉灵，马思聪，蔡文方

（1. 国网浙江省电力有限公司 电力科学研究院，浙江 杭州 310014；2. 杭州意能电力技术有限公司，浙江 杭州 310014；3. 河北省电力机械装备健康维护与失效预防重点实验室（华北电力大学），河北 保定 071003）

0 引言

双级轴流式动叶可调风机广泛应用燃煤电站，特别是660 MW、1 GW燃煤机组中。单列引风机优点是能简化机组烟风系统、降低厂用电、节约运维成本，可节约新建机组的设备采购成本、场地费[1,2]。

汽电双驱引风机[3,4]因具有高效、灵活、安全可靠等特点，而应用于大型发电厂中。部分轴流式动叶可调引风机在调试或运行中，时常发生叶片磨损、裂纹、轴承损坏、流道谐振等故障[5-9]，对机组安全运行造成影响。

文献[10]介绍了在中间轴、风机叶轮上进行动平衡、降低风机振动的方法。文献[11]介绍了在引风机二级叶轮上的双平面动平衡案例。文献[12-14]介绍了在引风机双平面进行动平衡及结构加固的案例；发现在引风机前后轮毂上进行双平面动平衡，可大幅降低残余不平衡量。对于工作转速在1 500 r/min 的轴流式动叶可调一次风机，文献[15,16]均采用双平面动平衡方法来有效降低残余不平衡。

本文对轴流式引风机典型长跨中间轴双悬臂转子结构进行了振动特性分析，讨论了其振动来源及不平衡离心力对轴承的受力影响，提出了振动治理措施。通过一台660 MW 超超临界燃煤机组轴流式引风机的振动处理实例验证了所用方法的可行性。

1 引风机振动特性分析

1.1 结构特征及振动特性分析

双级轴流式动叶可调引风机轴系，一般由电机转子、中间轴和风机转子所组成。风机一级、二级叶轮位于轴承座两侧，为双悬臂结构。因容量、风机烟道布局不同，引风机中间轴的长度会有所不同。引风机轴系如图1（a）所示。发电机、引风机转子均为刚性转子，由电机两侧端盖和风机轴承座作为支撑点。轴系动平衡位置位于风机叶轮轮毂和中间轴（接长轴）两端。轴系典型低阶振型如图1（b）所示。

图1 轴系结构及振型示意图Fig. 1 Diagram of shaft structure and vibration mode

引风机支撑为轴承箱结构，其轴承型式为滚动轴承，忽略阻尼后，其速度响应如公式（1）所示。

式中：Av为振动速度幅值；F为激振力；C为结构刚度；ω为振动频率；ω0为固有频率。

（1）离心力对振动的影响

中间短轴、联轴器以及叶轮存在的不平衡量，体现为作用在转子上的工频离心力。该力致使轴系产生1 倍频振动分量，其频率为fn=n/60（n为轴系转速，r/min），作用于轴系的离心力：

式中：M为转子质量，kg；e为转子偏心值，m；n为风机转速，r/min；t为时间，s。

风机转子在出厂前已经完成高速动平衡试验，所以残余不平衡量较小。在安装、运行后，中间轴、风机叶轮会出现一定的不平衡量，这会导致轴系不平衡量增加。

（2）中心偏差对振动的影响

一方面，联轴器中心安装较差时，轴系通常会出现2 倍频分量的振动，f2n=2n/60。另一方面，单平面配重后，风机转子力偶不平衡，将导致其中心发生变化，也会产生2 倍频分量的振动。

（3）叶片通过频率对振动的影响

若动叶或导叶出现裂纹、调节系统不佳等情况，则在气流激振力的作用下，在动叶上会产生通过频率为fy的振动分量[17]。若叶轮叶片数为y，则通过频率为fy=yn/60。另外，该情况也可诱发叶片共振频率的振动分量。

（4）轴系共振

引风机的工作转速较低，一般为750 r/min，部分为980 r/min；其一阶临界转速设计值均大于工作转速的1.2 倍。引风机转子为刚性转子。引风机与驱动电机间的联轴器较长，故导致其临界转速有所降低。同时，由于膜片式对轮为刚柔联轴器，若安装存在偏差，也会导致引风机临界转速的下降、风机的工作转速和临界转速的偏差较小，进而诱发轴系共振。

（5）风道流场不稳定对振动的影响

若进汽道或排汽烟风流场不稳定，当其激振频率fq和动叶或导叶的固有频率接近或重合时，会产生共振现象[18,19]。排汽烟风流道频率为：

式中：t为烟风温，℃；C为流场声速；k为阶数，取值为1、2、3；H为烟道高度，m。

1.2 引风机不平衡原因分析

由于锅炉烟道布置缘故，电机和风机之间布置的空心中间轴较长，其长度均大于5.6 m。

引风机工作环境的温度通常在90 ℃～130 ℃左右。考虑机械热膨胀，为补偿冷、热态的温度变化，在安装时，会使电机中心比风机水平中心高。

另外，烟气中所含的硫化物、氮化物等，会使叶片结垢、磨损，同样会导致转子出现质量不平衡。

引风机与电机的转子之间通过带有中间轴的膜片式联轴器进行连接，型式为挠性联轴器，可弥补中心偏差的影响。

1.3 离心力对轴承增量力的影响分析

在引风机2 级叶轮轮毂上同时或单侧加重的轴承支撑力增量如图2 所示。

图2 转子配重轴承受力变化示意图Fig. 2 Schematic diagram of bearing loads variation due to balance weight on rotor

若风机轮毂1、2 处存在残余不平衡量m1、m2，轴承A、B 将产生附加反力F1z、F2z。这2个力的根源为不平衡量m1、m2所产生的离心力F1和F2，于是有：

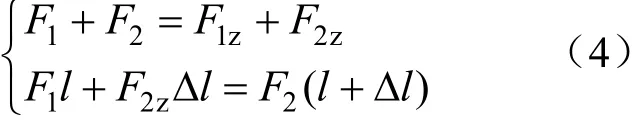
式中：F1=0.011m1r1n2、F2=0.011m2r2n2分别为1 级、2 级轮毂上不平衡量产生的离心力，N；l为轴承中心线至轮毂中心线的水平距离，m；Δl为两轴承中心线水平距离，m。

整理后得：

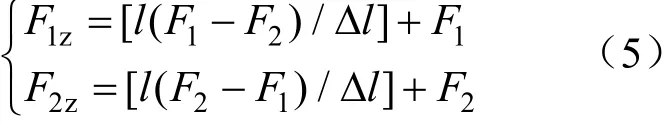
将风机叶轮上的不平衡量分成3 种情况。

（1）一级、二级轮毂上残余不平衡量为对称分量，即m1=m2=m，相位角相同。此情况下，轴承座上的受力变化较小，式（5）化为：

式中：r为离心力半径，m。

对于2 级轴流式引风机，残余不平衡量的半径大小相当。

（2）一级、二级轮毂上残余不平衡量为反对称分量，即m1=m2=m，相位角相反，则式（5）改写为：

由（7）式可知，此情况下，轴承座上承受的增量力变化较大。随着Δl的减小，l/Δl将会增大，即F1z、F2z增幅较大。

对引风机而言，l/Δl值通常在0.8～1.2 之间；A、B 轴承的支撑力变化量为不平衡量的3 倍左右。增幅过大，易导致轴系失稳。

此外，由于2 个轴承受力不均，所以会在2 个轴承上出现较大的力偶Mf=(Δl+2l)mrω2，使轴系产生轴向涡动，并导致风机的径向和轴向振动增大。

电机和风机间的中间轴较长，易产生较大的轴向扭转，这会导致径向振动的2 倍频分量较大。

（3）两端不平衡部位既非对称也非反对称

若一级叶轮、二级叶轮上存在不平衡量m1、m2，则可将其分解为一对对称分量与一对反对称分量。

引风机转子为刚性转子，对称分量占比较大，反对称分量占比较小。若对风机进行单端加重或反对称加重，均会使风机转子出现反对称不平衡分量，导致风机轴瓦的支撑力大幅增加。

综上所述：对于转速较低的内支撑双级轴流式引风机现场动平衡，应采用双面对称加重为主、单面加重为辅的配重方式；这样可大幅降低轴承因动平衡而产生的增量力，避免出现力偶不平衡诱发的轴系不稳定。

1.4 振动监测条件分析

理想监测条件：要实现高效双平面动平衡，应在电机、中间轴、风机的2 轴承上分别加装振动探头，最好是两相互垂直的振动传感器。

因受现场安装条件限制，通常只能在电机、风机轴承座两端加装振动传感器。有些厂家只在电机驱动端、风机轴承座两端加装有振动传感器，也可实现振动测量。

带有装键相信号的引风机振动监测系统，可为振动监测和后期振动分析与处理提供便利。

另外，各类型风机振动监测系统应当规范化，即振动传感器型号、位置均应一致。这样，动平衡后所得到的参数就具有通用性，可提高振动治理效率。

1.5 振动处理流程

在振动测量时，应首先对数据进行频谱分析。若振动频谱以1 倍频分量为主，则进行分量法分解，分析转子振型，进而选择在风机一级、二级叶轮轮毂上、中间轴上配重；若以其他频率为主，则应视情采取相应的治理措施。

将上述分析结果应用于大型轴流式动叶可调引风机振动故障诊断与处理中，流程如图3 所示。

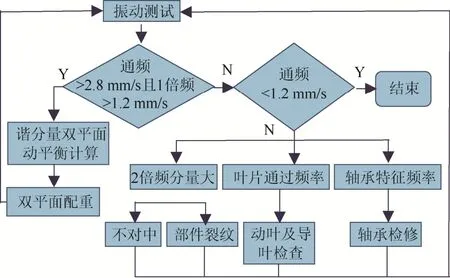
图3 引风机故障诊断及处理流程示意图Fig. 3 Flow chart of fault diagnosis and treatment process for fans

2 660 MW 单列引风机的振动处理

2.1 技术参数

某电站超超临界660 MW 汽轮发电机组：选用东汽D660BM 汽轮机，技术参数为28/600/620。

锅炉侧风机均为单侧配置，其引风机采用转速745 r/min 的AP 风机，其技术参数见表1。

表1 1 号引风机参数表Tab. 1 Parameters of No. 1 fan

配有EPRO600 振动测量系统。系统在电机驱动端、风机轴承上各装有3 个垂直安装的速度传感器。

2.2 振动现象

首次试转中，在风机外壳水平方向上加装2个速度传感器，用于测量风机壳体振动。

测量结果：振动值分别为4.8 mm/s、4.9 mm/s，1 倍频分量分别为3.5 mm/s、3.5 mm/s。诊断为转子存在动不平衡。

初步措施：在第一级叶轮轮毂上配重4.3 kg、逆转向20°后，振动有所减低。

重新配重：经计算，应在第一级叶轮轮毂上配重7.5 kg，逆转向43°。重新配重后，风机振动有所增大，电机驱动端、风机驱动端、自由端振动量分别为2.1 mm/s、4.4 mm/s、3.5 mm/s。

将SK9172 振动测试仪接入EPRO600 振动监测系统进行测试。测试结果为：风机驱动端、自由端的振动1 倍频分量分别为0.86 mm/s、2.4 mm/s，且以反向分量为主；同时，存在大量的2 倍频分量以及高倍频分量。测试结果见表2 和图4。

表2 单侧配重后振动数据Tab. 2 Vibration data after adding unilateral balance weight

图4 单侧加重后振动频谱Fig. 4 Vibration spectra after adding unilateral balance weight

2.3 振动分析

2.3.1 轴承受力分析

在风机一级叶轮轮毂上配重4.3 kg、逆转向20°时，振动有所减小，未见恶化现象；这表明转子上的确存在不平衡现象。

当风机单侧配重7.5 kg 后，虽然1 倍频分量有所下降，但2 倍频分量和叶频通过频率增加。

假设风机2 级轮毂上存在对称不平量为3.5 kg。在一级叶轮上加重3.5 kg，相当于二级叶轮上存在3.5 kg；而在一级叶轮上加重7.5 kg，相当于一级、二级叶轮上出现了反对称不平衡量为3.5 kg。

根据风机结构总装图，l=646 mm，Δl=470 mm，r=940 mm。不同加重下的轴承受力变化计算结果见表3。

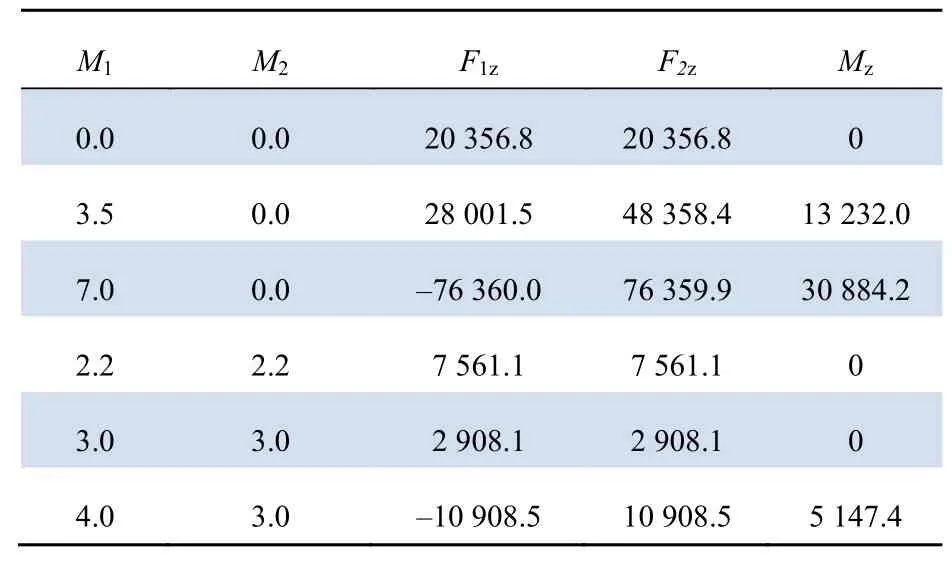
表3 不同配重下轴承受力变化Tab. 3 Bearing load variation under different balance weights N

在一级叶轮轮毂上逐渐增加单端配重量，一号、二号轴承的受力逐渐增加，且在风机转子上出现了较大的力偶不平衡。若把一级叶轮轮毂等分后分别配重到一、二级叶轮上，则一号、二号轴承的受力逐渐减小。轴承增受力增大，诱发转子不稳定状态，体现在1 倍频分量振动有所下降，但2 倍频分量和叶频通过频率增加。

因此，应采用在2 级轮毂上分别加重的方案：将7.5 kg 的不平衡块拆除，在一、二级叶轮轮毂进行对称分量动平衡。

2.3.2 其它部件固有频率分析

在停机期间，使用本特利VB8 振动测试仪，采用敲击法测试对引风机动叶、导叶、转子进行固有频率测试，结果如表4 所示。

表4 风机各部件固有频率测试结果Tab. 4 Results of tested natural frequencies of each fan component Hz

由表4 知，风机动叶一阶固有频率为28.6 Hz，与25 Hz（2 倍频）分量频率接近；且动叶三阶固有频率为251.5 Hz，与叶片通过频率（引风机的叶片个数为20 个，转速为745 r/min，叶片通过频率为250 Hz）接近。可推断出，风机可能会存在25 Hz、250 Hz 的结构共振。

由此推断，单端动平衡后，风机轴承座振动中出现25 Hz、250 Hz 分量，其原因为：一方面，风机与电机的联轴器中心配合较差，诱发了2 倍频分量振动。另一方面，风机动叶的固有频率可能与转动频率、叶片通过频率接近，触发共振。

2.4 振动治理

在风机一、二级叶轮轮毂两侧焊接平衡块，质量均为2.2 kg，逆转向25°。

配重后启动中，风机最大振动为3.2 mm/s。运行时，振动数据见表5 和图5。

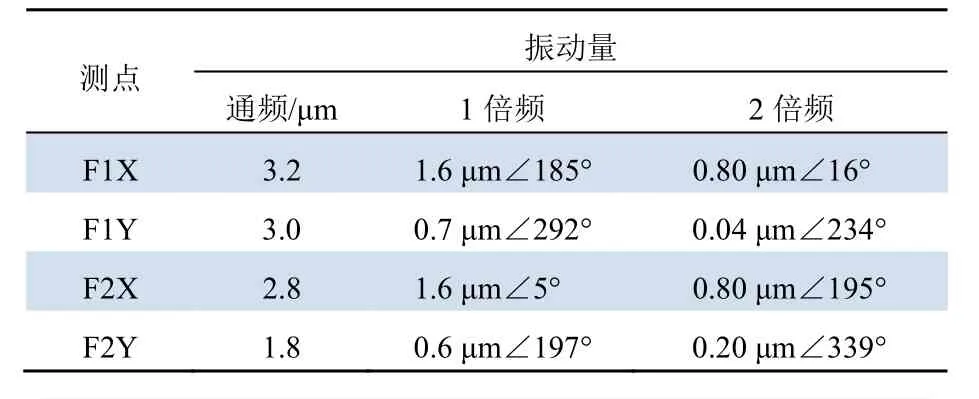
表5 两侧配重后振动数据Tab. 5 Vibration data after adding balance weights on both sides

图5 叶轮轮毂两侧配重后振动频谱Fig. 5 Vibration spectra after adding balance weights on both sides of the impeller hub

由表5 和图5 可知，平衡块调整后，风机振动有所减小，风机驱动端、自由端振动的1 倍频分量为1.6 mm/s，说明还存在一定的动不平衡量，可进一步进行动平衡。

经计算，还需在一级叶轮轮毂上配重1.5 kg，逆转向30°；在二级叶轮轮毂上配重0.8 kg，逆转向42°。

经过2 次配重后，风机振动降低至1.2 mm/s以下，1 倍频分量小于0.6 mm/s，2 倍频分量、叶片通过频率均大幅下降，具体结果见表6 和图6。

表6 第2 次两侧配重后振动数据Tab. 6 Vibration data after twice balance weights added on both sides

图6 第二次动平衡后的驱动端X 方向振动频谱Fig. 6 Vibration spectrum in X direction of drive end after twice dynamic balance

通过2 次双平面动平衡配重，风机振动水平为优良。在基建调试、168 h 后的投产运行中，风机均安全稳定运行。

2.5 现场动平衡策略

基于上述分析，引风机现场动平衡步骤为：

对振动测试所得的1 倍频分量进行谐分量分解；选择最佳配重平面；动平衡计算；动平衡处理。

在文献[12]等相关文献中，因仅采用了双平面影响系数动平衡法，所以至少需要进行3 次动平衡才能将振动降低至最小；而本文采用分量法和影响系数法相结合的方式，则最多进行二次动平衡就可将振动降低值最小值。

3 结论

（1）对于内支撑动叶可调引风机，较大的单平面平衡量对风机轴承所受的增量力的影响较大，可诱发轴系不稳定，引起高频谐波分量的振动；而双面动平衡对转子轴承所受的增量力的影响很小，不会诱发轴系失稳。

（2）当引风机配重质量较大时，采用双平面对称的加重方式可显著增加轴流式引风机的安全可靠性。

（3）应将轴系稳定性计算和现场振动测试相结合，设计合理的风机轴系结构，尤其是增加2轴承的跨距，可以从本质上提升引风机轴系稳定性，降低风机转子的加重量。