不同碳约束机制下微能源系统多目标优化决策

陈 娟，曹鑫鹏，鲁 斌

（1. 华北电力大学 经济管理系，河北 保定 071003；2. 华北电力大学 计算机系，河北 保定 071003；3. 复杂能源系统智能计算教育部工程研究中心（华北电力大学），河北 保定 071003）

0 引言

随着气候变化的不断加剧，能源利用的转型成为必然。微能源系统可以为当前能源利用的转型提供有效支撑。

微能源系统耦合了电力、热力等系统，在实现了能源高效梯级利用的同时，减少了长距离能源输送所造成的损失，有效提高了能源利用的安全性和灵活性。

微能源系统的规划涉及众多因素，如何实现系统决策最优成为研究的重点。

针对系统优化调度，文献[1]构建了优化调度模型，并对实例问题进行求解；文献[2]考虑可再生能源消纳率及碳排放指标，建立了微能源系统多目标优化调度模型；文献[3]引入综合需求响应概念，考虑了不同形式能源间的相互转化关系。此外，文献[4]提出了兼顾经济性与可靠性的微能源系统优化配置框架；文献[5]构建了能源枢纽以提高区域微能源系统能源利用率；文献[6]给出了包含经济性优化和可靠性校验的分层园区微能源系统优化规划方法。

在能源系统的绿色化发展的要求下，碳约束成为能源系统规划需要考虑的关键因素。文献[7]讨论了碳税和气价对分布式系统和燃煤电厂经济性的相互影响；文献[8]将碳排放交易机制和绿色证书交易机制引入电力系统环境经济调度；文献[9]构建了基于古诺模型的绿色证书交易模型，实现了可再生能源消纳和碳排放总量控制；文献[10]讨论了计及需求响应和阶梯型碳交易机制的多能耦合微能源系统优化调度；文献[11]讨论了碳交易和绿证交易制度下的电力批发市场能源优化模型。

目前，在关于能源系统优化决策的相关研究中，尽管考虑了碳减排目标、提出了环保性目标，并将可再生能源的消纳作为了减排的重要措施，但是：研究中缺少了将分布在用户端的屋顶光伏纳入协同的相关规划；同时，系统优化模型中并未考虑多种碳约束机制，缺少了对于不同机制的比较分析。

本文面向多碳约束机制，在综合考虑经济成本、减排目标的前提下，构建了不同约束机制下的微能源系统优化模型，以满足多元用能需求；采用改进粒子群算法求解了不同情景下的系统成本，给出了系统优化决策依据。

1 微能源系统

微能源系统承载着区域能源互联网的功能：以能源站为中心，利用互联互通的能源网络，将系统中各个参与主体连接在一起，实现能源的开放共享和交换共享[12]；在更便利地满足用户需求的同时，提供多类型能源服务，实现各类资源的优化配置[13]。与采用单向、封闭发展模式的传统能源系统相比，微能源系统通过将屋顶光伏、分布式能源站等新型元件分布在用户端，就地完成能源生产、输送以及消纳，从而减少了由于长距离供能带来的能源损失，是未来分散式能源体系的重要组成部分[14]。

本文所讨论的微能源系统的结构如图1所示。

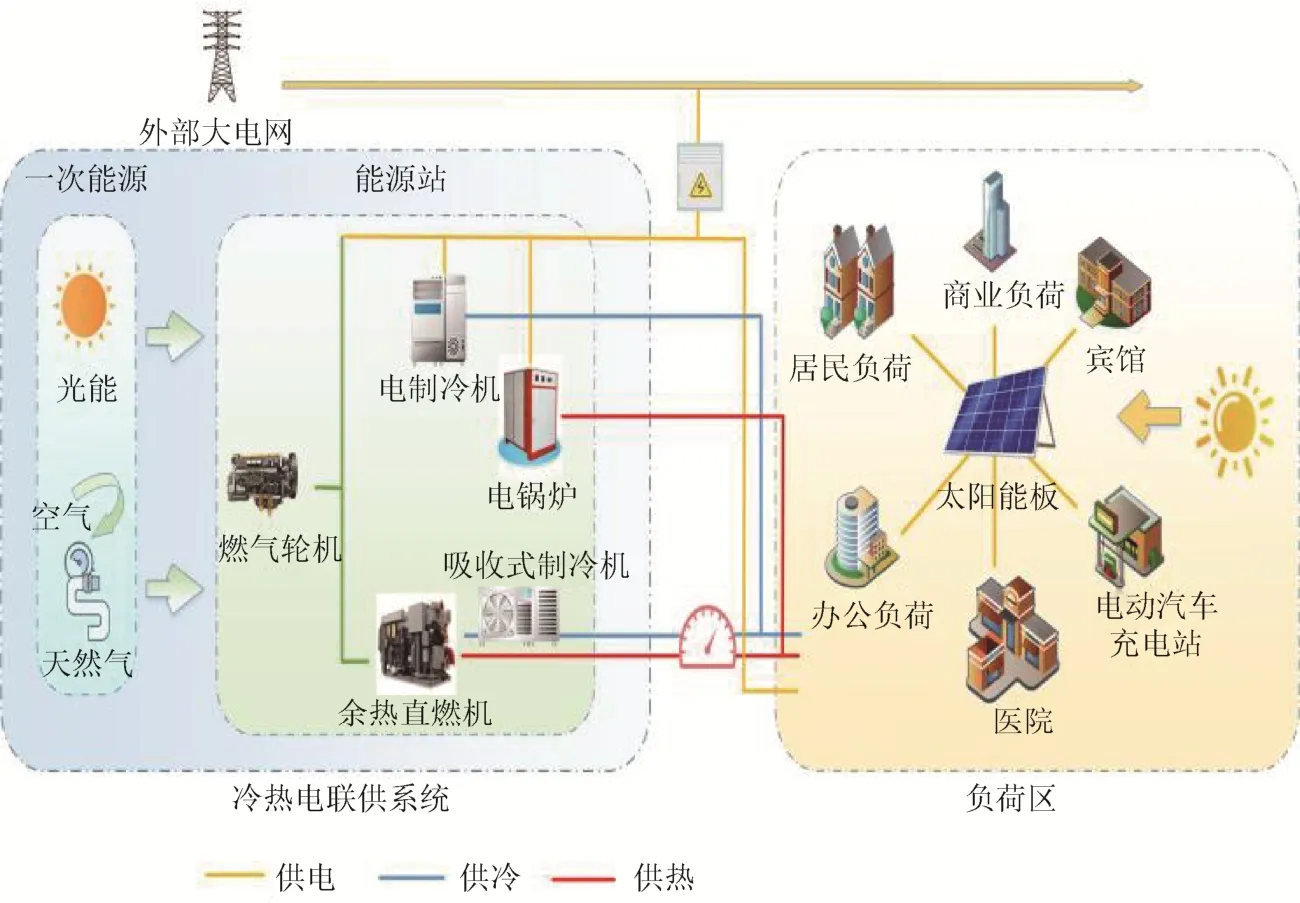
图1 微能源系统结构图Fig. 1 Structure diagram of micro energy system

系统以一次能源天然气为主，以太阳能为辅；在燃气冷热电三联供支持下，终端能源消纳表现为电、热、冷3 种能源形式；负荷类型主要有居民负荷、办公负荷、商业负荷、宾馆、医院、电动汽车充电站。另外，系统连接外部大电网，采用并网上网的运行方式[15]。

碳约束机制的实施能够直接对微能源系统中各机组的运行成本产生影响，从而达到改善系统供能结构、促进系统低碳化发展的目的。现阶段，我国减排机制正在不断完善。关注不同碳约束机制下的微能源系统优化及其可能产生的影响，有助于能源系统的科学规划与有效运行[16]。

新型能源系统的构建势必需要充分考虑碳排放问题。这一方面是应对气候变暖做出的主动应对，另一方面也是我国减排目标实现的必然路径[17]。

2 多目标优化模型

微能源系统运行的经济成本和碳排放量存在相互制约的关系。

在系统运行过程中，温室气体排放将产生环境负收益；因此，本文引入碳约束机制，将其转化为环境成本，与经济成本共同构成系统总成本。

考虑碳税、碳排放权交易和绿证交易在能源系统减排的过程中作用机制不同，故建立不同碳约束机制下的多目标优化模型。

2.1 系统模型构成

（1）燃气轮机发电

燃气轮机以天然气为输入，其数学模型为：

式中：Eg,dr为燃气轮机发电量，kW·h；Fg为天然气一次能源的消耗量，m3；ηge为天然气的发电效率。

（2）余热直燃机

余热直燃机的作用是对燃气轮机发电余热进行回收。回收后输出的热量为：

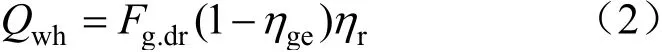
式中：Qwh为余热直燃机回收后输出的热量，kW·h；ηr为余热回收装置效率。

（3）吸收式制冷机

余热直燃机将热量输送至吸收式制冷机。制冷机组回收热量后输出的冷量表示为：

式中：Qac为吸收式制冷机制冷量，kW·h；COPac为制冷系数。

（4）电锅炉

当燃气发电机组产生的余热不能满足用户热负荷需求时，则利用电锅炉制热进行补充。电锅炉产生的热量可以表示为：

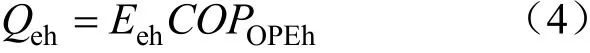
式中：Qeh为电锅炉供热量，kW·h；Eeh为电锅炉供热消耗的电量，kW·h；COPOPEh为电锅炉供热效率。

（5）电制冷机

当燃气发电机组产生的余热不能满足用户冷负荷需求时，则利用电制冷机制冷进行补充。电制冷机产生的冷量可以表示为：

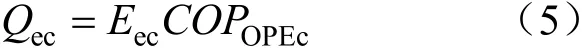
式中：Qec为电制冷机供冷量，kW·h；Eec为电制冷机供冷消耗的电量，kW·h；COPOPEc为电制冷机供冷效率。

（6）用户负荷

对规划区域用户的负荷采用单位面积法进行预测。用户负荷可以表示为：

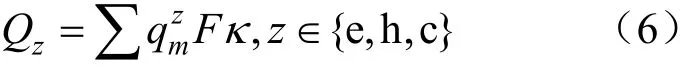
式中：Qz为z类能源的区域总负荷，kW·h；e，h，c 分别表示电、热、冷能源类型；为m类建筑单位面积负荷，kW·h/m2；F为建筑面积，m2；κ为同时使用系数。

（7）功率约束条件

系统中各类负荷需要满足平衡条件，具体如下：

热功率平衡约束为：

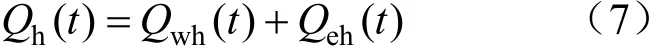
冷功率平衡约束为：

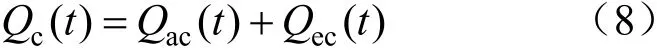
电功率平衡约束为：

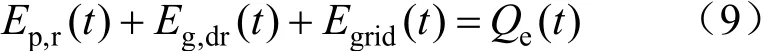
式中：Qh(t)、Qc(t)、Qe(t)分别为t时刻用户的热负荷、冷负荷、电负荷，kW；Ep,r(t)、Eg,dr(t)、Egrid(t)分别为t时刻屋顶光伏发电量、燃气轮机发电量、向外部电网所购/售电，kW。

（8）屋顶光伏约束条件

考虑用户屋顶装设太阳能发电装置，利用太阳能光电技术为用户供电。屋顶光伏的发电功率受装机容量制约，而装机容量又受屋顶面积的约束，具体如下：

式中：PPV为太阳能发电系统的输出功率，kW；VPV为屋顶光伏板的装机容量，kW；Aroof为区域屋顶总面积，m2；ηpr为光伏板容量系数。

2.2 规划目标函数

考虑经济性成本与碳排放量后，微能源系统优化目标函数为：

经济性成本为：

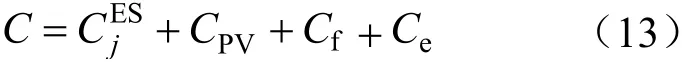
碳排放量为：

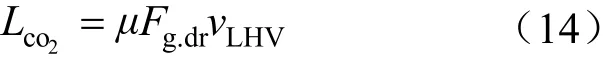
式中：μ为燃烧单位天然气产生的CO2，g/W·h；vLHV为天然气燃烧热值，kW·h/m3。

2.2.1 经济成本

（1）能源站年均总成本

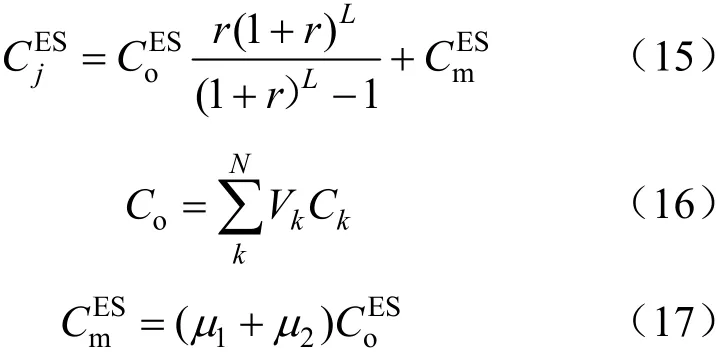
（2）屋顶光伏成本

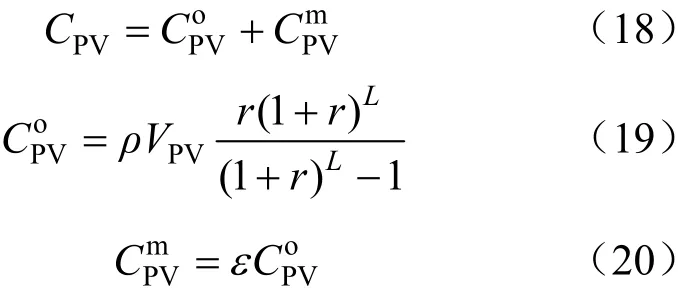
（3）系统运行费用

式中：Fg为天然气消耗量，m3；Cg为单位天然气价格，元/m³。

（4）系统购电费用

式中：Egrid为与外部大电网的成交电量，kW·h；Ce为单位电价，元/kW·h。

2.2.2 不同碳约束机制下的系统总成本

不同的碳约束机制下，系统环境成本不同，从而会影响系统前期设备配置、设备出力，进而影响经济成本、系统总成本以及碳排放量。因此，需要建立不同碳约束机制下的目标函数，通过比较选择最优的系统配置方案。

（1）碳税机制

考虑在碳税政策下微能源系统总成本最低，目标函数为：

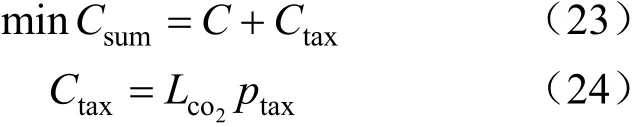
式中：Ctax为缴纳碳税成本，元；Lco2为实际碳排放量，kg；ptax表示为碳税价格，元/kg。

（2）碳交易机制

考虑在碳交易政策下微能源系统总成本最低，此时目标函数为：

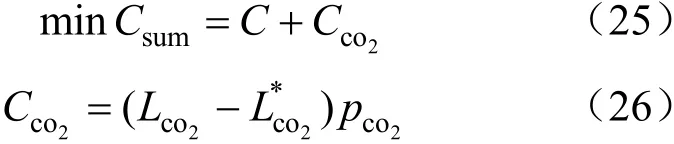
式中：Cco2为碳交易成本，元；为碳配额，kg；pco2表示为碳交易价格，元/kg。（3）绿证交易

考虑在绿证交易政策下微能源系统总成本最低，此时目标函数为：

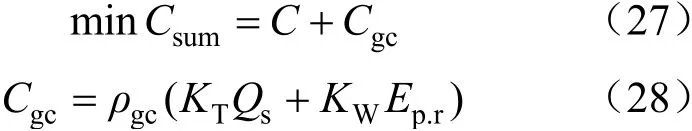
式中：Cgc为绿证交易成本，元；ρgc为绿色证书单价，元；KT、KW分别为燃气轮机和太阳能生产单位电能的绿证交易配额系数，KT＜0，KW＞0。

（4）碳交易和绿证交易

考虑在碳交易和绿证交易政策下微能源系统总成本最低，此时目标函数为：

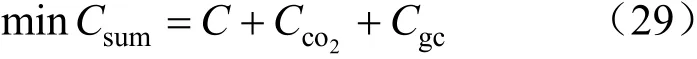
在以上4 种碳约束机制模型中，碳排放量指标均转化为环境成本，而环境成本分别由碳税、碳交易和绿证交易表示。通过分析可知，碳税、碳交易模型中的目标函数直接受实际碳排放影响；绿证交易模型则是受燃气轮机和太阳能出力影响，与碳排放间接相关。

2.3 求解算法

综合能源系统由于其内部存在多种能量转化设备和光伏发电设备，且冷、热、电能源相互耦合，因此其数学模型为非线性整数优化问题。智能算法被广泛应用于求解此类问题。

相较于遗传算法、蚁群算法等常见智能算法，粒子群优化算法（PSO）复杂度较低且易于实现。

由于PSO 容易陷入局部最优解，因此本文采用一种改进压缩因子的优化算法(FPSO)[18]对微能源系统多目标优化模型进行求解。

相对于传统的粒子群算法，该算法引入了新的压缩因子方程U，并改进了速度迭代公式，故能够有效避免诸多粒子困于某个局部的情况发生，从而提高了算法的收敛速度和收敛性能。

压缩因子为：

式中：c=c1+c2，c＞2。

FPSO 的具体运算步骤如下。

步骤（1）初始化粒子群。设置参数包含：群体规模M、粒子i随机初始位置和速度每个粒子的初始化位置Pbest(i)以及全局最优Gbest(i)。

步骤（2）计算每个粒子的目标函数值f(i)，并将其与个体极值Pbest(i)比较。如果f(i)＜Pbest(i)，则用f(i)替换Pbest(i)。

步骤（3）将步骤（2）中的每个粒子的f(i)和Gbest(i)比较。如果f(i)＜Gbest(i)，则用f(i)替换Gbest(i)。

步骤（4）对Pbest(i)和Gbest(i)值进行更新，并计算粒子新的运动速度和位置xik。

步骤（5）判断M值是否达到最大，如果达到则停止迭代，否则返回步骤（2）。

FPSO 的具体流程图如图2 所示。

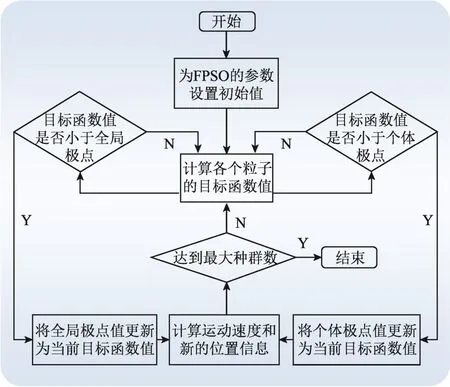
图2 FPSO 流程图Fig. 2 Flow chart of FPSO

3 算例仿真

以某省某规划区域为算例，对其进行仿真分析。利用MATLAB 对模型进行求解，分析不同约束机制下系统优化的结果。

3.1 算例条件

算例区域面积为12 km2，负荷类型包括居民楼、办公楼、商场、电动汽车充电站、医院以及宾馆。

根据算例区域气候特征，得到其负荷区域各类型建筑指标如表1 所示[19-20]。

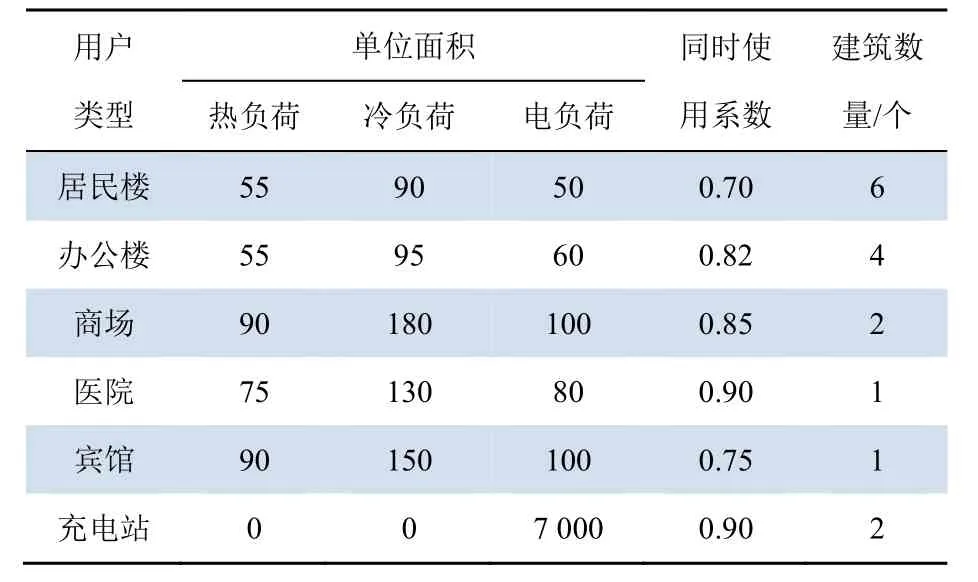
表1 算例各类型建筑指标Tab. 1 Indicators of various types of buildings in the calculation example W/m2

依据减排机制，本文分别设置了考虑碳税政策、考虑碳交易政策、考虑绿证交易政策和同时考虑碳交易和绿证交易的4 种减排情景。根据不同情景得到系统不同配置和成本。

算例中各相关参数如表2 所示[21]。

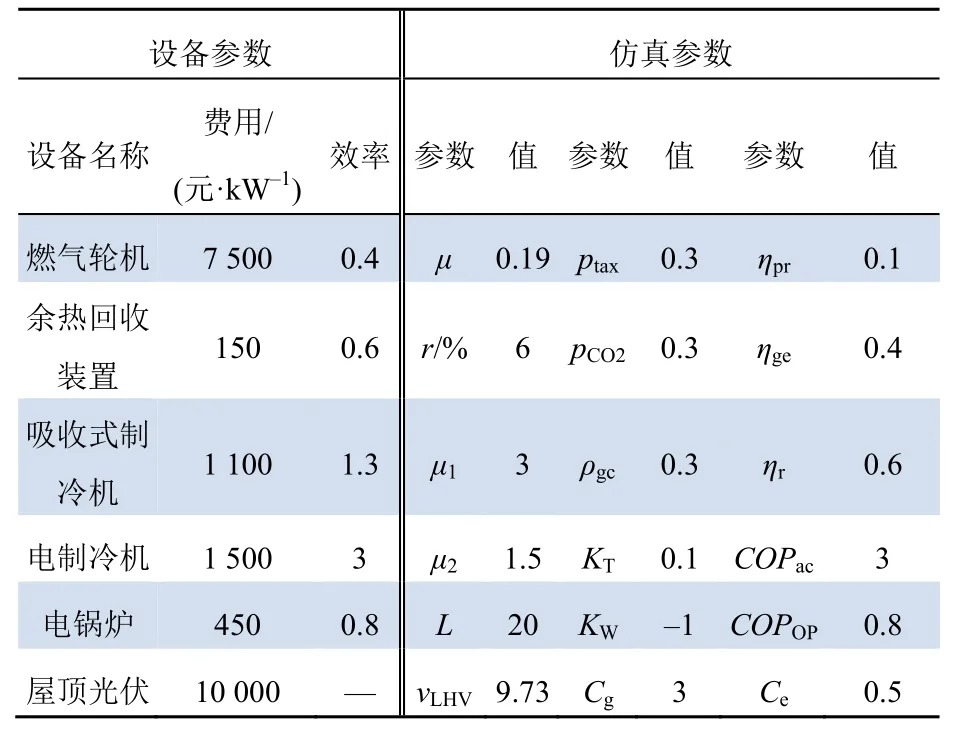
表2 算例设备及仿真参数Tab.2 Example equipment and simulation parameters

3.2 仿真结果与分析

为了验证算法的适用性，分别用基本粒子群算法和改进收缩因子后的粒子群算法对微能源系统多目标优化模型进行求解。通过优化系统内设备配置，使得系统总成本最小。

图3为2 种算法适应度的对比图：适应度表示系统总成本；粒子位置和速度的变化则分别反映设备容量及其调整量的变化。

图3 算法效果对比图Fig. 3 Comparison diagram of the algorithm effect

从图3 可以看出，FPSO 算法收敛速度快，且适应度曲线相对平滑；相较于PSO 算法，FPSO算法能够迅速跳出局部极值，未出现明显陷入局部最优解情况。

采用FPSO 算法时，系统总成本最终收敛于1.31×108元；采用PSO 算法时，收敛于1.37×108万元，为局部最优解。

由此可见，采用FPSO 算法在对该模型进行求解时，其收敛速度和收敛性能均优于PSO 算法。

通过仿真计算，得到4 种碳约束情景下的微能源系统总成本、各单项成本及碳排放量，如表3所示。依据计算结果，绘制不同碳约束机制下的系统年均总成本曲线图，如图4 所示。

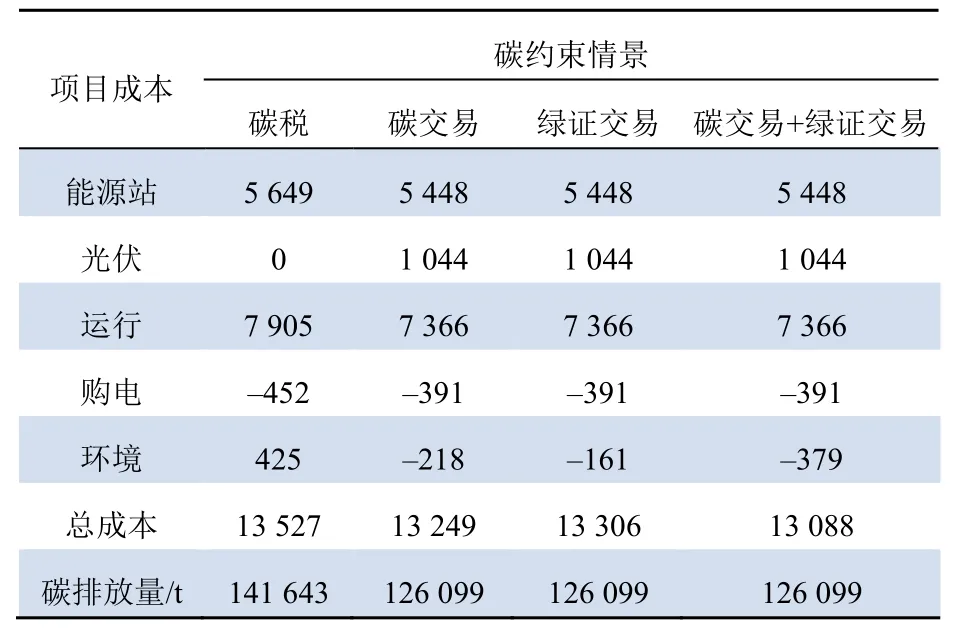
表3 不同碳约束情景下成本对比Tab. 3 Cost comparison under different carbon constraint scenarios万元

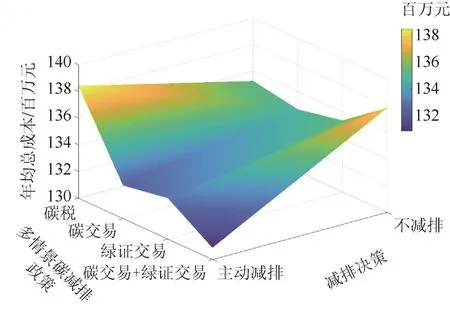
图4 多情景下不同减排措施系统总成本Fig. 4 Total system cost of different emission reduction measures under multiple scenarios

在每一种约束情景下，会有2 种决策可选择：一是调整设备配置、安装屋顶光伏实现主动减排；另一种是不改变设备配置且不安装屋顶光伏，而是缴纳碳税或购买碳排放权补偿排放。从优化结果可以看出，4 种情景下的系统总成本从低到高排序为：绿证交易+碳交易（主动减排）、碳交易（主动减排）、绿证交易（主动减排）、碳税（不减排）。

不难发现，相比单一约束机制，在碳交易和绿证交易的协同约束机制下，通过调整设备配置、安装屋顶光伏主动减排的方式能够实现系统成本最小的经济目标。

进一步对4 种碳约束情景下的系统各单项成本进行比较，结果如图5 所示。

图5 多情景下各项成本示意图Fig. 5 Schematic diagram of various costs under multiple scenarios

从图5 可以看出，相较于碳交易、绿证交易和碳交易+绿证交易协同机制，在碳税机制下，能源站设备成本、运行成本、环境成本以及碳排放量均更高，而屋顶光伏成本和购电成本则更低。这是由于：其余3 种情景通过主动减排，调整了能源站设备配置容量，可以使设备成本降低；增加屋顶光伏设备可以减小能源站内燃气轮机发电比例，使得天然气消耗量减小，进而使运行成本

、碳排放量和环境成本均得到有效降低。

此外，碳税机制下的环境成本为正，其余3种情景均为负，表明碳税的缴纳对微能源系统产生的环境负外部性并不能直接校正。反之，在碳交易和绿证交易机制下，通过在市场中出售二氧化碳排放权和绿证来获得奖励，减排产生正外部效应的同时获得直接收益。

4 种约束情境下，购电成本均为负，这意味着系统不仅能够满足自身用电需求，还可以通过对外售电获得收益，体现了微能源系统的独立性。

通过以上分析比较不难看出，碳交易和绿证交易的协约束机制对于微能源系统的减排目标来说更具有积极性。

4 结论

本文构建了计及碳约束的微能源系统多目标优化模型，并采用改进的粒子群算法对算例进行验证，得到了如下结论：

（1）碳约束机制直接影响了微能源系统中设备的配置，对提升系统经济性及环境效益、增加可再生能源利用率、降低系统碳排放量具有显著作用。

（2）碳税机制属于事后补偿，对碳排放量减少效果不明显，缺乏长期减排效应。

（3）碳交易和绿证交易的协同约束，可使决策者主动实施优化系统配置、增加可再生能源使用等减排措施，并通过市场机制使得所获的利益最大化，使微能源系统实现全局最优，进而保证了减排的长期效应。