基于价格弹性矩阵的用户响应潜力评估方法

张若愚，刘 敏，李 震

（1. 贵州大学 电气工程学院，贵州 贵阳 550025；2. 贵州电网有限责任公司 电网规划研究中心，贵州 贵阳 550002）

0 引言

新能源设备的大规模接入给电力系统的稳定运行带来了巨大的挑战，仅仅依靠供给侧的调节并不能较好地解决实时的供需平衡问题[1]。

电价机制是电力市场机制的核心。我国早期的电力市场执行固定电价。因固定电价并不能反映不同时段的边际供电成本，故出现了非高峰时段用户补贴高峰时段用户这一不合理情况[2]。通过价格信号引导，可促使用户改变用电行为，可激发用户需求响应潜力。近年来，分时电价作为我国主要的电价政策，基本上在全国得到了广泛的推广[3]。

在需求响应项目实施前，电网应当对响应资源有一定的了解。研究用户在分时电价下的需求响应潜力，这对分时电价政策的制定具有很大的意义。

国内外学者在需求响应潜力评估方面进行了一系列的研究。文献[4]针对不同类型的负荷进行分析并建立了对应的需求响应矩阵，量化了负荷削减和用电量转移的能力。文献[5]提出了一种基于概率的负荷识别方式，通过可控负荷获取用户的响应潜力。文献[6]采用非线性最小二乘法对空调灰箱模型中RC 的参数进行估计，分析了不同控制策略下用户空调的响应潜力。文献[7]将用户的负荷减少建模为不确定的高斯分布；通过训练一个混合密度循环神经网络，输出用户响应潜力的概率分布。文献[8]基于改进的物元可拓模型对用户进行分级，评估需求响应能力。文献[9]基于静态和动态参数估计获取空调工作状态和环境参数；依据该参数评估了工厂和商业负荷的响应潜力。文献[10]构建了变频空调的物理模型，评估了空调集群的响应潜力，确定了最优控制策略。文献[11]提出了一种获取空调工作状态的状态识别方法，得到了空调集群的响应潜力。文献[12]基于非侵入式负荷分解获取了用户可中断负荷比例，聚合得到了负荷的响应能力。

目前，对于量化用户需求响应潜力的相关研究甚少。文献[13]采用问卷调研的方式分析了我国某地区第二产业各部门的响应潜力。文献[14]设计了调查问卷，获取了用户的响应潜力相关信息，分析了响应潜力的影响因素。文献[15]采用模拟实施DR 项目的方式，分析了用户在不同激励政策下的用电行为；结果表明，响应时长和季节是响应潜力的主要影响因素。上述文献只分析了响应潜力的影响因素，未实现具体量化。

因此，本文以居民公寓为研究对象，对用户的需求响应潜力进行了描述和量化：首先，在传统需求价格弹性矩阵（price elasticity matrix of demand，PEMD）的基础上，引入弹性影响权重对模型进行了改进。然后，形成响应潜力的综合评价指标，从需求响应容量和需求响应速度2 方面对居民用户在每个用电时刻、不同用电时段的响应潜力进行了描述。最后，基于改进的PEMD模型对用户的响应潜力进行了量化，从而得到用户每一时刻的响应潜力。

1 改进PEMD

1.1 传统PEMD

在经济学中，需求的价格弹系数常被用来反映商品的需求对价格变动的敏感程度，通常表示为[16]：

式中：ε为商品价格弹性系数；Q为该商品的原始需求量；ΔQ为该商品响应价格而引起的需求变化；P为商品的价格；ΔP为该商品的价格变动。

ε越大，表示商品需求对价格变化的敏感程度越高；ε为0，则表示需求对价格变动完全不敏感。

电力价格的变动对电力需求的影响并不是单一的。电力价格的变动在影响本时间段用电量的同时，也会导致其他时间段间电量的相互转移。

按照其在PEMD 中的位置，电价弹性系数可分为自弹性系数、交叉弹性系数2 种。

自弹性系数εii，是时间段i的用电需求变化对时间段i电价改变的反映，体现了电力需求自身的增减，表示为：

式中：Qi和ΔQi为时间段i的原始电力需求及电力需求的变化量；Pi和ΔPi为时间段i的原始电价和电价的变化量。

交叉弹性系数εij，是时间段j的用电需求变化对时间段i电价改变的反映，体现了电力需求的相互转移，表示为：

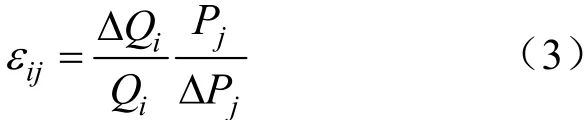
考虑某个用电周期T，将其划分为n个用电时间段，建立n阶PEMD，表示为E。

1.2 基于弹性影响权重的改进PEMD

在传统的电量电价弹性矩阵中，某个时间段i内的用电变化量ΔQi是由2 部分构成的：（1）由本时间段的电价变化ΔPi引起的用电量增减；（2）其他时间段电价变化ΔPj引起的用电需求转移。

由负荷特性可知，用户通常会响应电价变化而对本时间段用电量做出调整，但对其他时间段电价变化引起的负荷转移并未表现出较大的意愿。显然，本时间段i的电价变化对用电量变化的影响要大于其他时间段。

为了体现这一特性，引入文献[1]中弹性影响权重这一概念，用于表征不同时间段电价对用电量的影响程度，以削弱除时间段i外其他时间段的影响程度。

弹性影响权重δ定义为：某时间段电价变化对某时间段用电量变化的影响程度。

用δij表示由时间段j的电价变化在时间段i产生的用电量变化ΔQij和时间段i的总用电变化量ΔQi之比，表示为：

式中：ΔQi和ΔQij可分别由式（6）、式（7）确定。

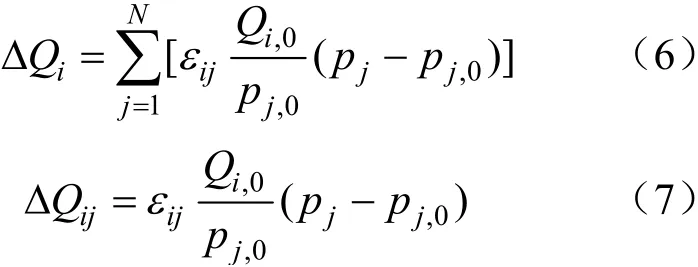
式中：Qi,0和pj,0分别为分时电价前时间段i的用电量和时间段j的电价；pj为时间段j的分时电价。

需要注意的是，其他时间段电价引起的电量变化ΔQij均与本时间段电价i有关，因此有由式（5）可知，iiδ=1 。

实施分时电价后，属于同一峰平谷时间段的用电时间段之间不会产生用电量的相互转移，即δij= 0；对于不同峰平谷时间段，则有0 ＜δij＜ 1。

引入式（5），对式（2）（3）和（4）进行修正，得到修正后电量电价弹性矩阵：

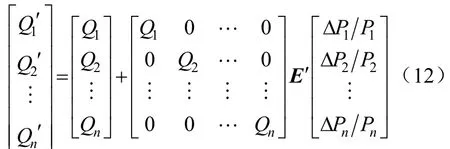
因此，用电量变化率和电价变化率之间的关系可表示为式（11）：

由式（11）可得出分时电价后用电量为：

2 需求响应潜力

2.1 需求响应容量

为表征参与响应的能力大小，定义用户在t时刻的需求响应容量为用户在每个用电时刻的负荷响应量，用峰时、平时和谷时的响应容量表示为：

式中：Pc(t)为t时刻负荷的响应容量；ΔQpp为用电峰时段负荷的削减量；ΔQpf为用电峰时段向平时段的负荷转移；ΔQpv为用电峰时段向谷时段的负荷转移；ΔQff为用电平时段负荷的变化量；ΔQfv为用电平时段向谷时段的负荷转移；ΔQvv为用电谷时段负荷的增加量；Tp、Tf和Tv分别表示用电峰时段、平时段和谷时段。

2.2 需求响应速度

需求响应速度被定义为需求响应容量对时间的变化率，其反映了负荷响应电价变化做出调整的速度快慢[17]。t时刻响应速度Ps(t)由负荷该时间点的响应容量Pc(t)决定。响应容量的变化速度越快，则负荷应对调度指令的响应能力越强，响应潜力越大。依据上述定义，用户在t时刻的需求响应速度可被表述为：

2.3 综合需求响应潜力

综上2 个需求响应潜力评价指标，对其归一化处理并以权重系数区分其重要程度，得到了评价用户响应潜力的评价指标。负荷在t时刻的综合需求响应潜力被表述如下：

式中：Pa(t)为t时刻负荷的综合响应潜力；P1(t)和P2(t)分别为归一化后的需求响应容量和需求响应速度；θ1和θ2分别为权重系数，并且有

当侧重考察负荷的削峰填谷能力时，θ1应当大于θ2；侧重考察负荷快速参与响应事件的能力时，θ2应当大于θ1；不区分重要程度时有θ1=θ2=0.5。

2.4 需求响应潜力的计算流程

需求响应潜力的计算流程如图1 所示。

图1 需求响应潜力计算流程Fig. 1 Demand response potential calculation process

由需求响应容量的定义不难看出，用户在t时刻的响应容量即为该时刻实施分时电价后负荷的变化量。因此，t时刻的响应容量Pc(t)可由式（12）确定：将式中右侧的原始负荷移至左侧即可得到各个时刻的响应容量。

由式（14）可知，要想获得用户t时刻的需求响应速度Ps(t)，则要求响应容量Pc(t)为连续函数。因为获得的实际数据只能是某一段时间内的负荷数据，所以数据呈现出离散性，于是式（14）便不再适用。

将t时刻的需求响应速度重新定义为：用户t时刻与其相邻时刻t-1 和t+1 的需求响应容量的变化率均值的绝对值，表示为：

式中：Rs(t)为t时刻负荷的离散化后的需求响应速度；Δt为采样的时间间隔。

由于起始时刻和结束时刻仅有一个相邻时刻，其响应速度被定义为和相邻时刻需求响应容量变化率的绝对值。

将上述确定的响应容量和速度带入式（15），便可获得t时刻负荷的综合响应潜力Pa(t)。同时，为了考察某段时内的响应潜力，将负荷某段时间内平均需求响应潜力定义为：

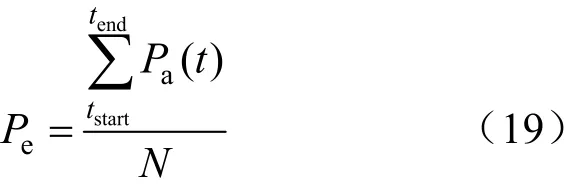
式中：Pe为某段时间内负荷的平均需求响应潜力；tstart，tend分别为某时间段的起始时刻和结束时刻；N为该时间段包含的时刻数。

3 算例分析

以4 个公寓某日用电负荷为算例。

用户负荷的采样间隔为1 h。取θ1=0.7，θ2=0.3。

为体现用户用电习惯，本文在用电谷时段的基础上进一步划分了不敏感用电谷时段，以表现弹性的大大降低。该地的电价政策如表1 所示，用户的自弹性和交叉弹性系数如表2 所示。

表1 用户电价政策Tab. 1 Policy of electricity price for users元/kW·h

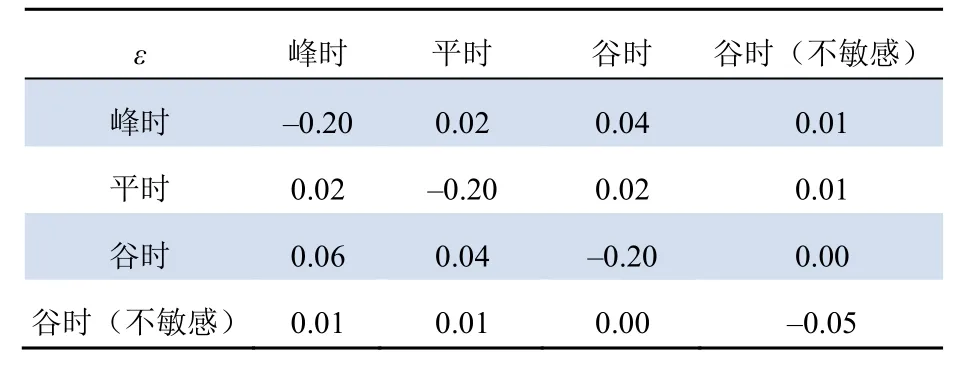
表2 用户电量电价弹性系数表Tab. 2 Electricity price elasticity factor for customers

用户实施分时电价后的负荷曲线可由式（12）确定。实施分时电价后的负荷曲线和归一化后响应潜力分布如图2—5 所示。

图2中，公寓1 的最大响应潜力出现在19:00；图3 中，公寓2 的最大响应潜力出现在12:00；图4 中，公寓3 的最大响应潜力出现在17:00；图5中，公寓4 的最大响应潜力出现在17:00：综合响应均为1.0，这说明在该时刻用户的响应容量和响应速度同时达到了最大值。

图2 公寓1 分时电价后响应潜力分布Fig. 2 Response potential distribution after TOU price in apartment 1

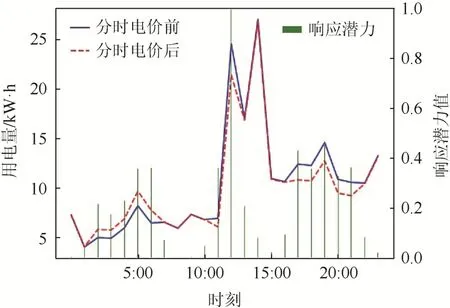
图3 公寓2 分时电价后响应潜力分布Fig. 3 Response potential distribution after TOU price in apartment 2

图4 公寓3 分时电价后响应潜力分布Fig. 4 Response potential distribution after TOU price in apartment 3

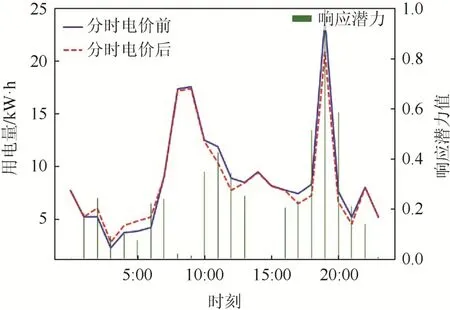
图5 公寓4 分时电价后响应潜力分布Fig. 5 Response potential distribution after TOU price in apartment 4

需要注意的是，响应容量和响应潜力并不是总能同时取得最大值。

该公寓群中另一公寓的负荷曲线和响应潜力分布如图6 所示。从图6 可以看出，虽然该公寓在11:00 达到了最大响应容量1.0，但其响应容量变化速度相较于其他时间点来说较为缓慢，仅为0.068；而23:00 虽然处于负荷低谷期，响应容量为0.807，但其响应速度达到了1.0。总的来说，处于峰荷的11:00 的综合响应潜力仅为0.721，而在23:00 则达到了最大值0.842。由于11:00 的响应速度较小，导致其不能参与快速变化的响应，使综合响应潜力有所下降。

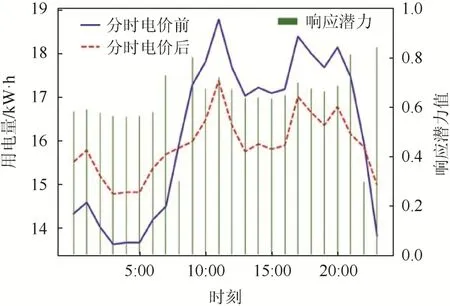
图6 某公寓分时电价后负荷曲线和响应潜力分布Fig. 6 Load curve and response potential distribution after TOU price in an apartment

公寓4 在表3 所示4 种不同的电价政策下的响应潜力变化情况如图7 所示。从图7 可以看出，随着峰谷电价浮动比的增大，用户的响应潜力逐渐增大。

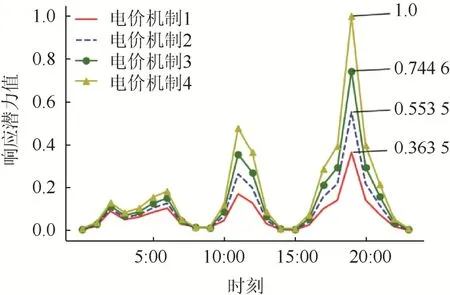
图7 公寓4 在不同电价政策下的响应潜力Fig. 7 Response potential of apartment 4 under different electricity price policies

表3 不同电价政策下的峰值负荷时间Tab. 3 Peak load time under different electricity price policies

但由表3 可知，在电价政策4 的情况下，用户的最大峰值负荷由19:00 转移到09:00。过高的电价拉开比导致了峰值负荷的转移。

为了研究不同用电时段划分对响应潜力的影响，图8 对比了公寓4 几种不同划分情况下响应潜力的变化情况。由表4 可知，在峰时段划分为16:00—19:00、17:00—20:00 和18:00—21:00 的情况下，公寓4 的日均响应潜力分别为0.084 7、0.135 6 和0.135 9；峰时段划分为11:00—13:00、18:00—21:00 和08:00—10:00、18:00—21:00 的情况下，公寓4 的日均响应潜力分别为0.182 6 和0.210 3。

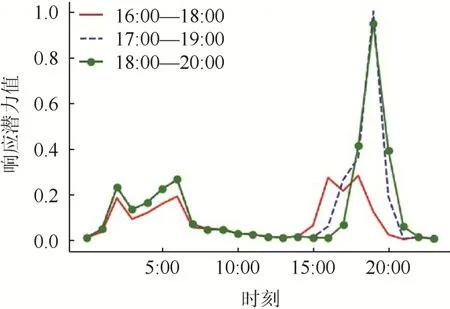
图8 公寓4 在3 种不同峰时段划分下的响应潜力Fig. 8 Response potential of apartment 4 in three different peak periods

表4 公寓4 在用电峰时段划分下日均响应潜力对比Tab. 4 Comparison of average daily response potential of apartment 4 under peak periods of electricity consumption

由公寓4 的负荷曲线可以看出，其用电高峰时间和第5 种时间段（08:00—10:00，18:00—21:00）的划分方式是相吻合的。因此，当用户的用电行为和用电时间段划分方式的重叠程度越高，用户的响应潜力越大。

图9所示为4 个公寓日响应潜力分布曲线。表5 给出了这4 个公寓在同一天内的日最大、日均响应潜力值。

表5 算例公寓的响应潜力比较Tab. 5 Comparison of response potential of the four apartments

图9 公寓的日响应潜力分布Fig. 9 Response potential distribution of apartments on a given day

从图9 及表5 可见，无论从最大或是日均来考察用户的响应潜力，公寓1 相比而言都具有最大的响应潜力，而公寓4 的响应潜力最小。出现这一现象的主要原因是公寓4 的用电情况和用电时间段划分的重叠情况较差，且峰值负荷略小于其余公寓。因此，若以现有电价政策实施分时电价，则应首先考虑公寓1 作为优质的响应资源。

4 结论

本文引入弹性影响权重，对传统的电价电量弹性矩阵进行了改进；从需求响应容量和需求响应速度2个方面定义了用户的综合需求响应潜力；基于改进的电价电量弹性矩阵量化了居民用户的需求响应潜力；研究了不同峰谷电价措施和时段划分方式对用户响应潜力带来的影响，得出如下结论：

（1）随着峰谷电价浮动比的增大，用户的响应潜力出现了逐渐增大的趋势；但过高的电价拉开比会导致峰值负荷的转移，从而出现峰谷倒置的现象。

（2）用电时间段划分情况和用户的用电情况的相似程度越高，则用户的响应潜力越大。

本文方法能够量化和评估用户的需求响应潜力，其结果对分时电价政策的制定和优质响应资源的选择具有一定的参考价值。