基于混合模型的风电机组异常数据识别方法

林立栋，郭 鹏，甘 雨

（华北电力大学 控制与计算机工程学院，北京 102206）

0 引言

SCADA（supervisory control and data aqurirement）运行数据能够反映风电机组的运行特性和状态。在实际运行过程中，由于天气、环境、机组停机、通信噪声和设备故障等因素，风电机组运行数据中存在大量异常数据。准确识别这些异常数据，才能有效提高后续以运行数据为基础的风电机组功率预测、发电性能评价、状态监测等工作的效率和精度[1]。

针对风电机组运行数据中异常数据的识别，文献[2]提出了变点分组与四分位组合的方法——在不同风速区间上依次使用变点法和四分位法，对数据中堆积型异常数据和分散型异常数据进行有效识别。该方法清洗数据的损失率偏高，且不能完全识别、清除所有类型的异常数据。

文献[3]提出四分位与DBSCAN（density-based spatial clustering of applications with noise）聚类相结合的异常数据清洗方法。因DBSCAN 算法对参数调整敏感，故该算法无法自动确定参数阈值，且对于高密度区域异常数据的清洗效果较差。

文献[4]采用局部离群因子（local outlier factor，LOF）算法来识别异常数据。该算法利用加权距离计算数据的相对密度，把具有足够高密度的区域划分为簇，实现了分散型异常数据的有效识别与剔除。但该算法无法有效识别分布密度较高的堆积型异常数据。

文献[5]提出基于图像处理的异常数据清洗算法：将风速-功率散点转换为风功率曲线的二值图像，然后根据风功率曲线图像中异常数据与正常数据的像素空间分布特征，通过图像操作剔除异常数据的像素。该方法所需数据量较大，且像素与数据之间无法一一对应，即无法直接给出单个数据的正常或异常状态。

文献[6]提出结合堆叠去噪自编码器（stack denoise auto-encoder，SDAE）和基于密度网格聚类方法的无监督异常值检测方法：利用SDAE 提取原始数据的特征，然后基于密度网格的聚类方法来得到聚类结果，最后通过设置窗口宽度实现对异常数据的识别。由于计算时需要花费大量时间去过滤原始SCADA 数据，故该方法效率低。

针对以上文献的局限，本文结合风电机组运行数据的分布特征，将参数模型与非参数模型结合，以实现风电机组异常运行数据的识别。以2 台风电机组所具有的复杂异常数据为例，验证本文所提方法的有效性。

1 数据分布特征分析

不同因素所产生的异常数据，在风速-功率（V-P）坐标系中的分布特征也各不相同。

功率散点：即每一条运行数据中，由风速和功率构成的数据对，简称为散点。

本文以2 台1.5 MW 双馈式风电机组（LY21和E17）10 min 间隔运行数据为算例。LY21 机组发电功率大于零的数据总计18 215 条，其散点分布如图1 所示；E17 机组发电功率大于零的数据总计30 205 条，其散点分布如图2 所示。

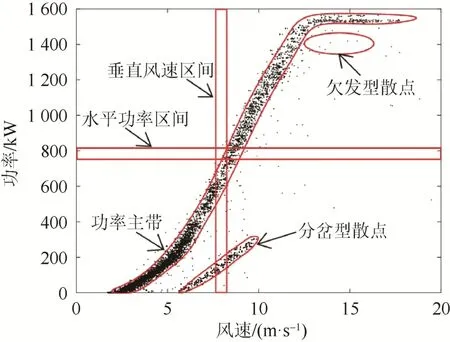
图1 LY21 机组功率散点分布Fig. 1 Power dots distribution of LY21 unit

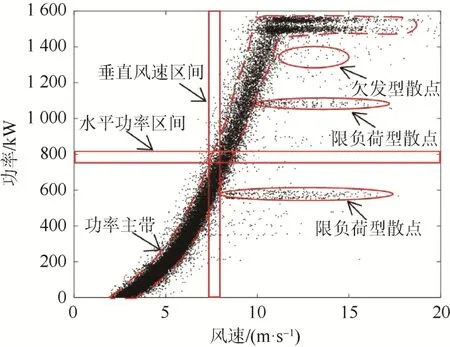
图2 E17 机组功率散点分布Fig. 2 Power dots distribution of E17 unit

从图1、图2 中可看出，2 台机组正常运行数据对应的功率散点分布密集，“功率主带”呈“厂”字形分布。将显著脱离风电机组正常运行状态的运行数据，即“功率主带”外的运行数据定义为异常运行数据，其所对应的功率散点即为异常散点。异常散点可分为以下3 类。

（1）欠发型散点。该类型散点表现为：随机分布在功率主带附近且密度较低，风速较高但功率较低。此类散点一般由于风电机组工况变化、数据采集异常、发电性能劣化等因素引起。

（2）分岔型散点。该类型散点表现为功率主带附近的一条或者多条密度较为稀疏的功率副带。此类散点产生的原因可能为风速计或转速传感器异常、变桨系统卡塞等。

（3）限负荷型散点。该类型散点表现为一条或多条位于功率主带右侧的横向密集堆积的水平数据带。此类散点产生的原因是：当机组出现弃风限电时，风电机组提前变桨，控制机组在限定功率状态下运行。

由于风电机组功率散点分布复杂，直接对风速-功率坐标系内所有功率散点进行异常数据识别的难度较大。因此，需要对功率散点进行分区，通过建立不同区间内的散点概率模型，实现对各区间内散点分布情况的准确描述，从而完成异常数据的识别。

参数模型，如正态分布模型、威布尔分布模型等，其优点是参数具有显著的物理意义，能够直观准确描述数据的整体分布特征，具有全局性。但是，使用参数模型需预知数据分布是否符合该模型特征，并需首先将水平功率区间内散点的分布转换为频率直方图，再用频率直方图数据拟合模型参数。如图1、图2 所示，2 台机组各水平功率区间数据分布情况复杂，无法直接判断其较为符合哪类参数模型，且频率直方图的分区宽度难以确定。

非参数模型，如核密度估计模型等，其优点是使用时无需事先知道数据的分布，仅从数据本身即可得到数据的概率密度分布；但是，因其缺少能直观描述数据整体分布特征的模型参数，所以其具有局部性，缺乏整体性。

本文将非参数模型与参数模型两者相结合。在未知各水平功率区间中数据分布前提下，首先应用非参数模型（扩散核密度估计）得到功率散点的概率分布；再引入参数模型对概率分布进行拟合，采用拟合的模型参数来准确描述数据整体分布特性。

2 扩散核密度估计概率分布

2.1 扩散核密度估计

核密度估计（kernel density estimation，KDE）是一种常见的非参数密度估计方法[7-9]。该方法可直接估计样本数据的概率密度，无需事先假设样本是否服从某个总体分布。

传统核密度估计的表达式为：

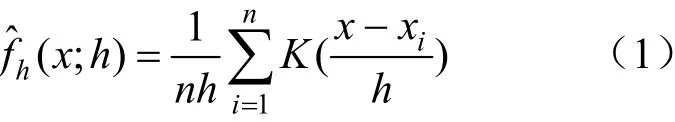
式中：x1,···,xn为总体样本的独立分布随机变量；n为样本数量；h为与n有关的常数，称为带宽或光滑参数；为核函数，本文选取高斯核作为核函数。

本文采用扩散核密度估计法（diffusion-based kernel density method，DKDM）替代KDE，有效解决KDE 带宽选取以及边界校正的问题，并提高KDE 的局部适应性[10]。

DKDM 将核函数等效于热扩散过程的转移密度，从而建立热扩散与普通核密度估计的联系。

DKDM 的核密度估计公式为：

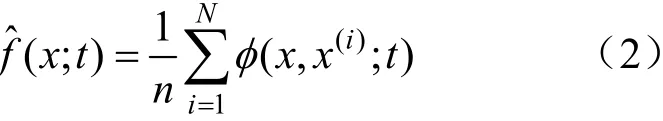
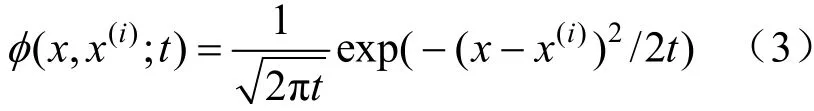
式（2）为下述傅里叶热扩散偏微分方程（diffusion partial differential equation，DPDE）的唯一解[10]：

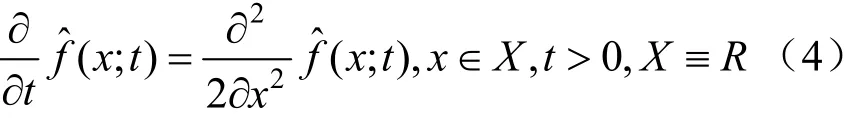
式（4）的初始条件为：

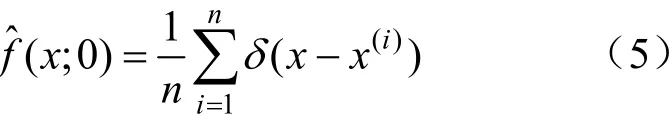
式中：δ为狄拉克函数。

当采用传统核密度估计时，若随机变量x的定义域有界，则需要对边界进行校正。若采用

DPDE，则仅需在初始条件（5）和诺埃曼边界条件式（6）下求解式（4）。

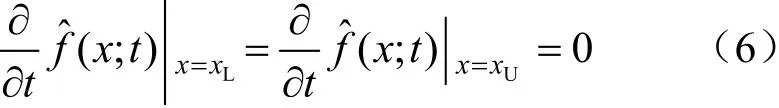
式中：xL为随机变量x定义域的下界；xU为随机变量x定义域的上界。

假设定义域为[0,1]，则基于扩散方程的核密度估计的解析解为[11]：

式中：κ为θ函数，其表达式为：

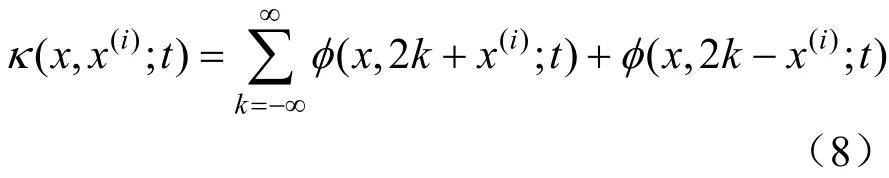
式（7）在式（1）的基础上，考虑到了带宽选择与边界校正，能够很好地解决传统核密度估计带宽选取和边界拟合误差这2 个问题。

2.2 水平功率区间功率散点概率分布

在满发状态时，机组运行在额定功率附近，此时产生的散点均属于正常数据，无需再进行分析；因此，本文仅对额定功率下的功率散点进行区间划分并做相应的分析。

为保证每个水平功率区间内包含足够多的散点，在本文中：水平方向上，将机组分为30 个功率区间；功率区间的间隔为50 kW。

用DKDM 估计概率分布，结果如图3 所示。

风电机组功率主带所对应的功率散点分布十分密集，因此该处概率密度估计值应明显较高。在图3 中，可以非常直观地看出，2 台机组的每一个水平功率区间中至少存在一个波峰，该波峰的概率密度值明显高于此功率区间中其余位置。结合图1、图2 及核密度估计的原理可知，该波峰对应的即为功率主带的中心位置。

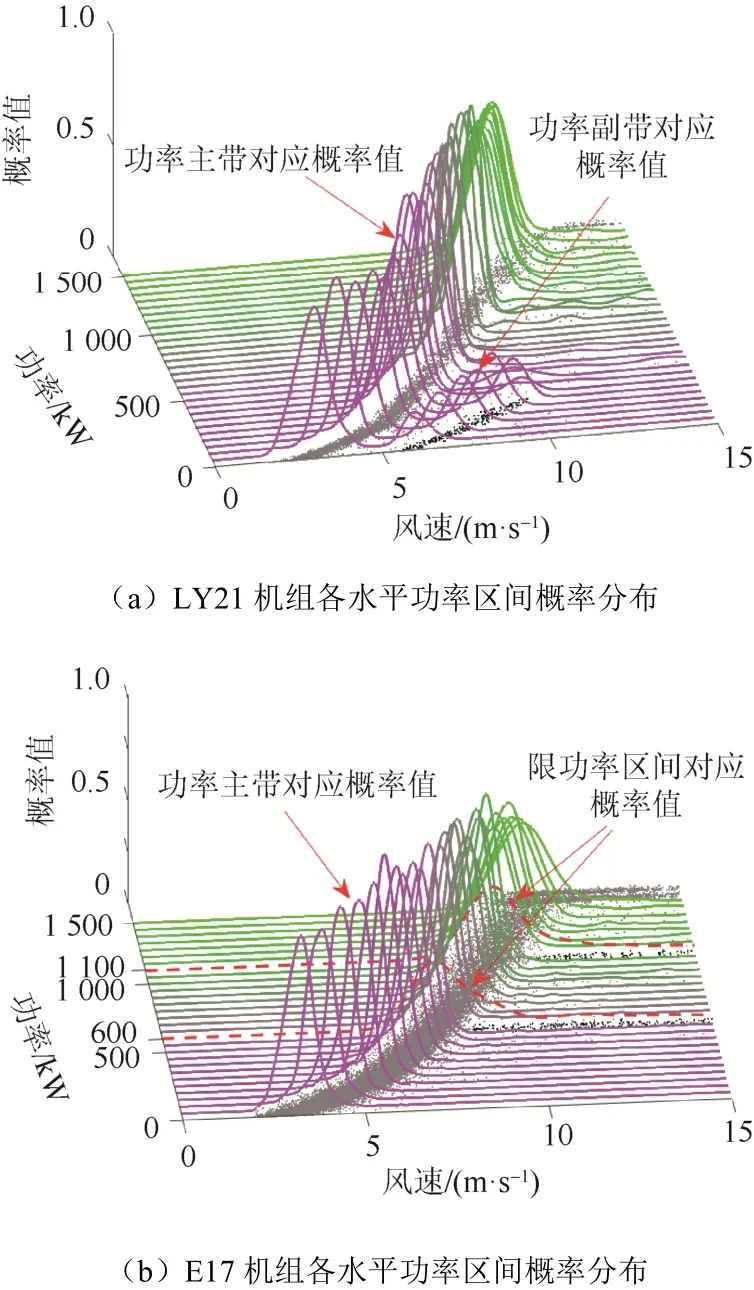
图3 DKDM 概率密度估计结果Fig. 3 Probability density estimation results by DKDM

LY21 机组前6 个功率区间（0～300 kW）的概率密度分布曲线均出现了双峰现象：在水平功率区间中，除功率主带对应的概率密度峰值外，还存在与图1 中分岔型散点（即稀疏功率副带）相对应的另一个分布密度低于功率主带的次峰值。

E17 机组各水平功率区间概率密度分布曲线均呈单峰现象。但是，在第12（550 kW～600 kW）和第22（1 050 kW～1 100 kW）个功率区间，可以明显看出其概率密度峰值远低于其它功率区间，且概率密度曲线水平向右延伸很远，呈现拖尾状态[12]。与图2 中对应位置的功率散点分布进行对照分析，结论为：在这2 个功率区间中，出现向右延伸的人为限负荷横向堆积型数据。

通过对每一水平功率区间内功率散点进行扩散核密度估计，将原来只能人为观察的散点疏密分布转换为数字概率密度曲线。但由于扩散核密度估计方法属于非参数模型，没有能够简单直观描述如LY21 机组双峰或E17 机组拖尾等水平功率区间的整体分布特征的模型参数。因此，本文采用参数模型，即混合威布尔分布模型，对扩散核密度估计的概率密度曲线进行参数化拟合；通过拟合参数提取和描述各水平功率区间散点的整体分布特征。

3 概率密度曲线参数拟合

威布尔分布模型常用于风速和风能概率密度估计[13-15]，但对于图2、图3 这样的概率密度曲线，用单一威布尔分布并不能达到很好的拟合效果[16]。

混合威布尔分布模型由多个单一威布尔分布加权组合而成。该模型的适用性较强，对于各种复杂概率密度曲线的拟合效果较好，且模型各参数的不同组合，可以反映出所拟合曲线形状的多种复杂特征[17]。拟合后，混合威布尔分布的权重、形状参数和尺度参数即可精确量化反映某一水平功率区间中扩散核密度估计概率密度曲线形状特征，即功率散点整体分布特征。

3.1 混合威布尔模型

假设一个总体样本可分为m个子体，每个子体均服从相同分布。假设各个子体的概率密度函数分别为f1(t),f2(t),…,f m(t)，各个子体所占的权重分别为p1,p2, …,pm。于是，混合威布尔分布的模型可表示为：

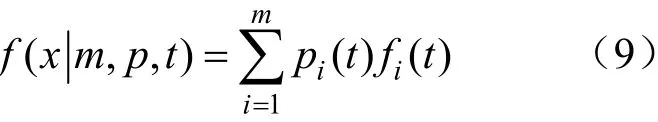
若每个子体都服从威布尔分布，则fi(t)为：

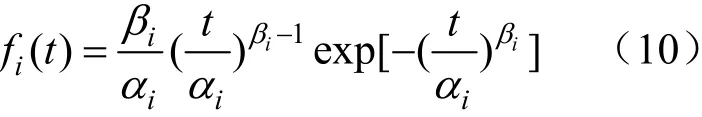
式中：αi为第i个威布尔分布尺度参数；βi为第i个威布尔分布形状参数。

本文采用混合威布尔分布对LY21、E17 机组各个水平功率区间概率密度曲线进行拟合。几个典型区间的参数，如表1 所示。

表1 混合威布尔典型参数Tab. 1 Mixed Weibull typical parameters

拟合效果如图4 所示。

从图4 中可看出，混合威布尔分布能够较好地完成对扩散核密度估计概率密度曲线的拟合。计算拟合曲线与概率密度曲线的均方根误差，发现均方根误差均小于0.04。这说明，拟合曲线能够准确反映水平功率区间内功率散点的分布情况。

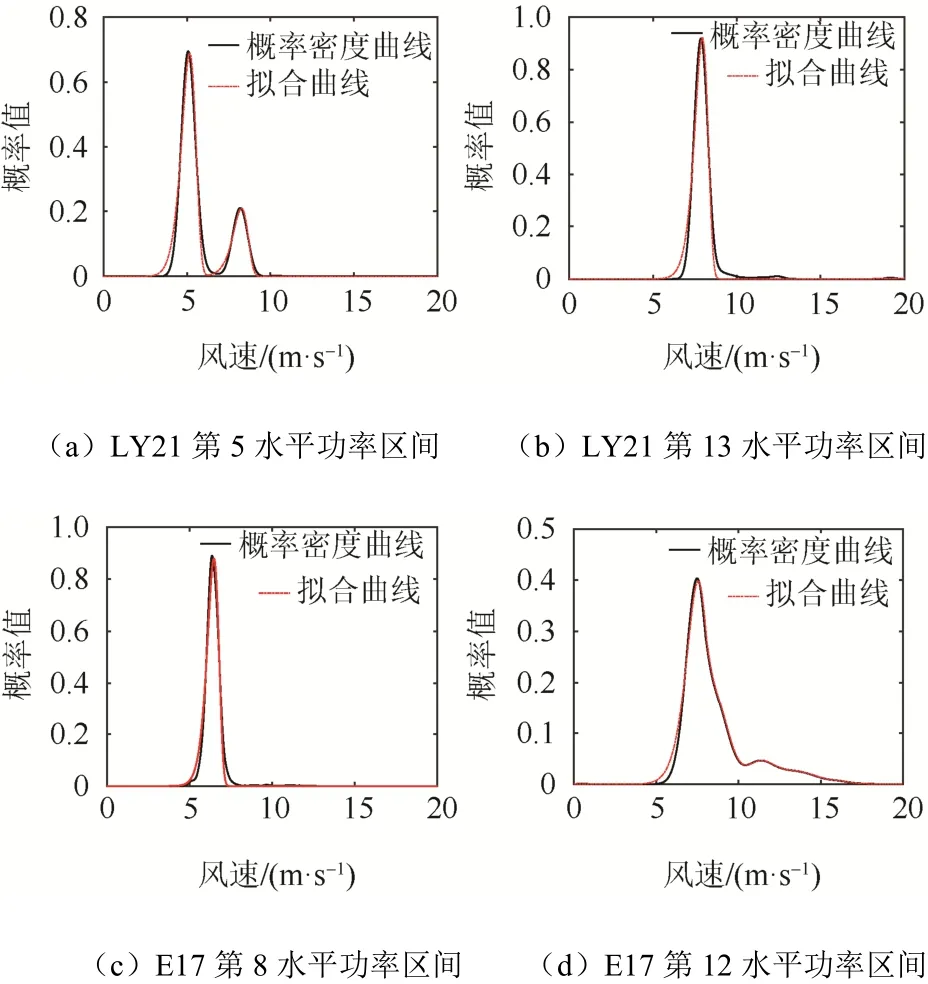
图4 混合威布尔分布对水平功率区间概率密度曲线拟合效果Fig. 4 Fitting effect of mixed Weibull distribution for probability density curves in horizontal power intervals

混合威布尔分布的权重p表示各子体数据在总体数据中所占比例。p的个数i代表着子体的个数。当i=1 时，为单峰情况；当i＞1 时，为多峰情况。

混合威布尔分布的形状参数β决定拟合函数的形状：当β≤1 时，拟合函数呈指数减函数；当β＞1 时，呈现尖峰特性[18]；当β＞3.5 时，整体形状与正态分布相似，且β越大，概率密度分布越集中在其峰值附近。

由表1 可知，LY21、E17 机组的形状参数β均大于3.5，这说明拟合曲线均呈现近似正态分布形状。

混合威布尔分布的尺度参数α主要起到拉伸整个函数的作用。α的大小决定拟合函数的陡峭程度：α越小，拟合函数越平缓，右侧尾部占比越大，呈“胖尾”特性；α越大，拟合函数越陡峭，尾部占比越小，呈“瘦尾”特性[19]。

根据混合威布尔分布3 个参数的定义以及表1 的具体数据，可分析得出LY21、E17 机组包含3 种类型水平功率区间：正常水平功率区间，限功率水平功率区间，分岔型水平功率区间。以下针对3 种类型详细说明。

（1）正常水平功率区间

以E17 机组第8 水平功率区间为例。具体计算结果如图5 以及表2 所示。

图5 E17 机组第8 水平功率区间散点及概率分布图Fig. 5 Dots and probability density distribution for the 8th horizontal power interval of E17 unit

表2 E17 机组第8 水平功率区间混合威布尔参数Tab. 2 Mixed Weibull parameters for the 8th horizontal power interval of E17 unit

考察表2 所示结果。E17 机组第8 水平功率区间仅包含一组参数p1、α1、β1，这说明：混合威布尔分布只拟合出一组参数，为单一威布尔分布；模型中只包含一个子体，概率密度曲线只包含单峰。同时由于α1的数值为23.23，数值较大，概率密度曲线呈现典型正态“瘦尾”特性，即概率密度曲线呈现瘦高、陡峭现象，不存在拖尾特性，如图5 所示；功率散点密集分布在功率主带上，符合正常功率散点的分布特征，因此判断该水平功率带为正常水平功率区间。

由此：若某一水平功率区间混合威布尔分布为单峰型，形状参数β＞3.5 且尺度参数α＞20，对应概率密度曲线呈现单峰、陡峭、不拖尾特性，可判断该水平功率区间中散点分布正常，为正常水平功率区间。

（2）限功率水平功率区间

以E17 机组第12 水平功率区间为例。具体计算结果如图6 以及表3 所示。

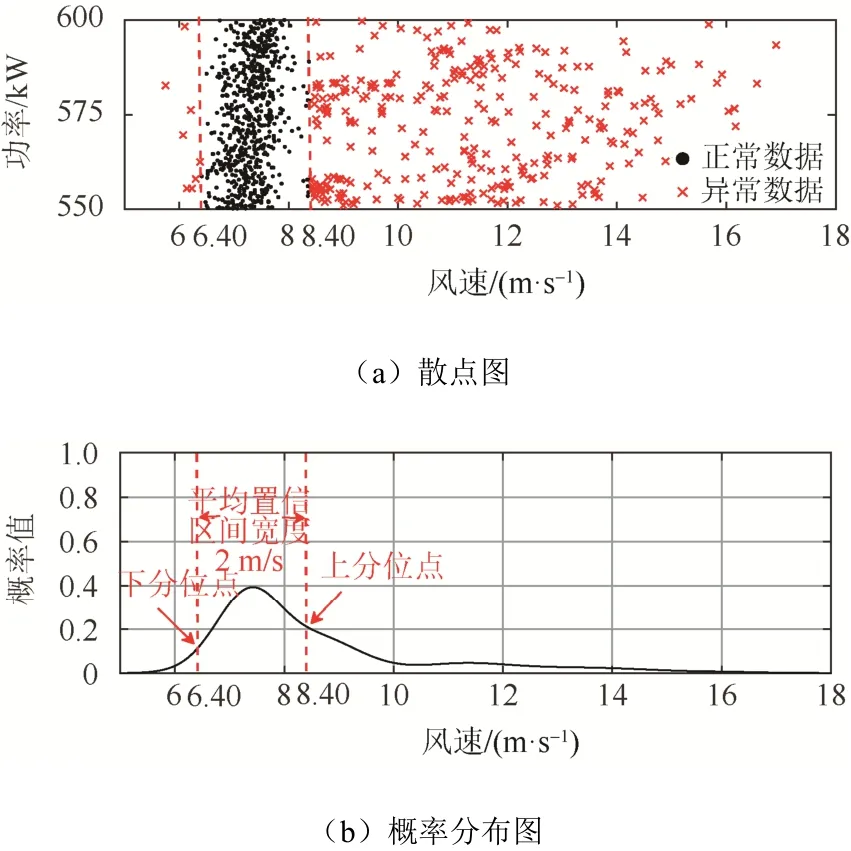
图6 E17 机组第12 水平功率区间散点及概率分布图Fig. 6 Dots and probability density distribution for the 12th horizontal power interval of E17 unit

表3 E17 机组第12 水平功率区间混合威布尔参数Tab. 3 Mixed Weibull parameters for the 12th horizontal power interval of E17 unit

考察表3 所示结果。E17 机组第12 水平功率区间仅包含一组参数p1、α1、β1。同上文所述，判断模型只包含单峰。E17 机组第12 水平功率区间α1的数值为9.39，显著小于其第8 水平功率区间的α1值（α1为23.23）。此时概率密度曲线呈现“胖尾”特性，即概率密度曲线呈现矮胖、右侧拖尾现象，如图6 所示。此时功率散点除分布在功率主带上，还存在水平向右延伸的密集堆积型散点，因此判断该水平功率带为限功率水平功率区间。

（3）分岔型水平功率区间

以LY21 机组第5 水平功率区间为例。具体计算结果如图7 以及表4 所示。

表4 LY21 机组第5 水平功率区间混合威布尔参数Tab. 4 Mixed Weibull parameters for the 5th horizontal power interval of LY21 unit

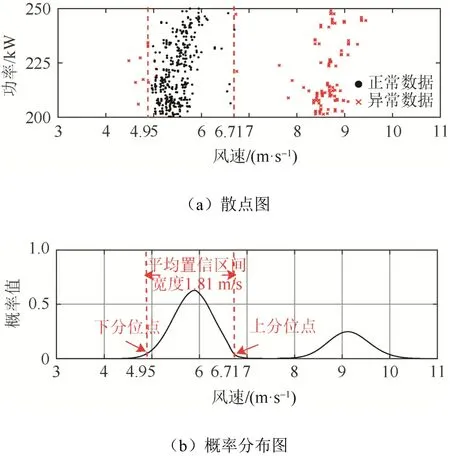
图7 LY21 机组第5 水平功率区间散点及概率分布图Fig. 7 Dots and probability density distribution for the 5th horizontal power interval of LY21 unit

考察表4 所示结果。LY21 机组第5 水平功率区间出现了2 组参数：p1、α1、β1以及p2、α2、β2。根据混合威布尔分布原理可知，此时所拟合的模型中包含2 个子体，即所拟合的模型中包含2 个威布尔分布，可判断出现了双峰现象。由于α1大于α2，表明LY21 机组第5 水平功率区间第一个峰比第二个峰更瘦更高，如图7 所示。此时功率散点除了密集堆积在功率主带上，在功率主带向右位置也出现了较为密集堆积的散点，判断该水平功率区间为分岔型水平功率区间。当多个相邻水平功率区间均出现此现象时（如LY21 机组第1至6 个水平功率区间），则反映为在功率主带右边出现分岔现象，即出现了一条稀疏功率副带。

对照分析可知，3 类典型水平功率区间的功率散点分布、对应扩散核密度估计概率密度曲线以及混合威布尔分布模型拟合参数所表达的结果完全相符。因此可以得出结论：混合威布尔分布的权重、形状参数和尺度参数，能够定量、准确地表征各个水平功率区间运行数据的整体分布特征，可作为判断该区间数据分布正常与否的重要依据。

3.2 基于平均置信区间的异常数据识别

对于异常数据较多的风电机组如LY21 和E17，除正常水平功率区间外，还存在如限负荷型、分岔型等非正常水平功率区间。

本文提出平均置信区间方法，分别对正常水平功率区间和非正常水平功率区间进行异常数据识别。

依据某一水平功率区间的混合威布尔拟合参数及上述正常水平功率区间的判别方法，即可确定该区间是否为正常水平功率区间。

（1）正常水平功率区间异常数据识别。

对于正常水平功率区间，以概率密度曲线峰值为中心，向左侧和右侧对称确定置信度为95%的双边分位点及置信区间宽度。置信区间内的功率散点即为正常数据，区间外的即为异常数据。如图5（b）中E17 机组第8 水平功率区间所示，其置信分位点分别为5.36 m/s 和7.40 m/s，置信区间宽度为2.04 m/s。

将机组所有判断为正常水平功率区间的置信区间宽度求取平均值即可得到平均置信区间宽度。E17 机组的正常水平功率区间共28 个，平均置信区间宽度为2.00 m/s。LY21 机组的正常水平功率区间共24 个，平均置信区间宽度为1.81 m/s。

（2）非正常水平功率区间异常数据识别。

对于通过混合威布尔分布拟合参数判定为具有拖尾或双峰等特征的限负荷、分岔型等非正常水平功率区间，采用平均置信区间方法识别异常数据。

以非正常水平功率区间的概率密度曲线最大峰值为中心，向左侧和右侧对称确定置信分位点，分位点之间的置信区间宽度为该机组的平均置信区间宽度。如图6 中，E17 机组第12 个限功率水平功率区间采用E17 机组的平均置信区间宽度2.00 m/s。图7 中LY21 机组第5 个分岔型水平功率区间采用LY21 机组的平均置信区间宽度1.81 m/s。置信区间内的功率散点为正常数据，区间外的为异常数据。

采用上述方法依次对额定功率以下的各个水平功率区间进行异常数据识别。LY21 和E17 机组的异常数据识别结果如图8 所示。图8 中，黑色散点表示正常数据，红色散点表示异常数据。

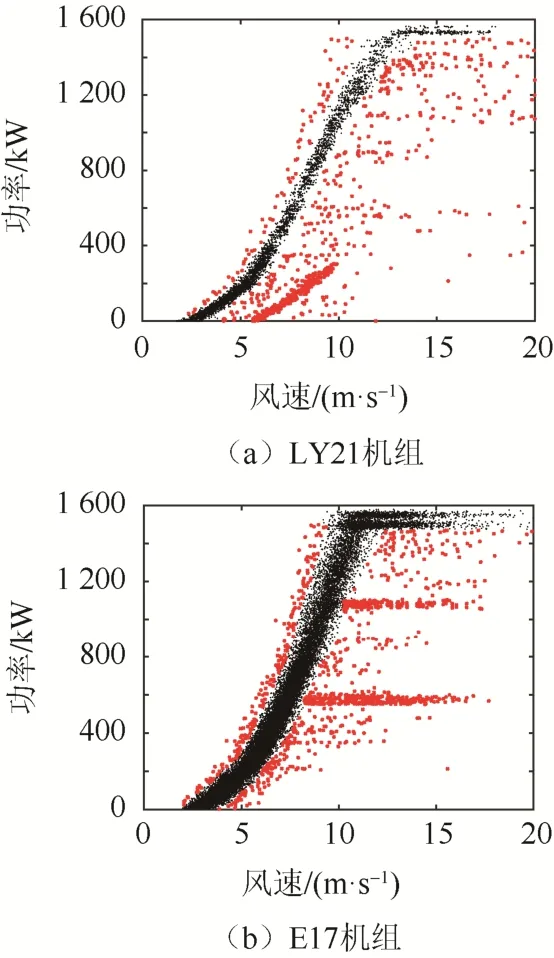
图8 异常运行数据识别结果Fig. 8 Abnormal operational data identification results

3.3 算法对比分析

文献[4]采用LOF（local outlier factor）算法对2 台实验机组进行异常数据识别。LOF 算法的思想是：利用加权距离计算数据的相对密度；把具有足够高密度的区域划分为簇；通过设定阈值，实现对异常数据的清洗。

对于本文算例，该算法识别效果如图9 所示。

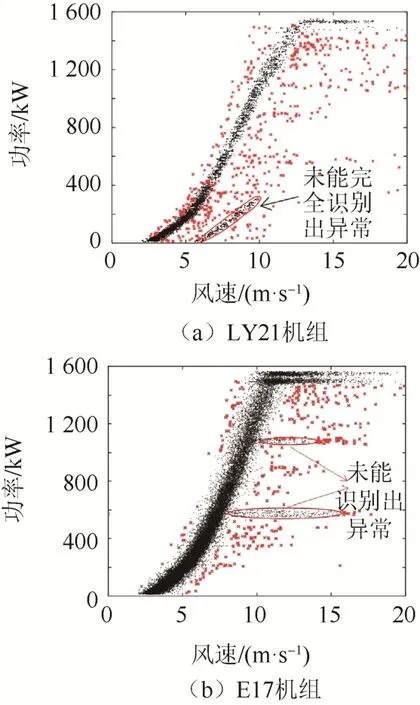
图9 LOF 算法异常运行数据识别结果Fig. 9 Abnormal operational data identification results

对于LY21 及E17 机组，本文所提方法的数据剔除率分别为12.6%与3.68%，LOF 算法的数据剔除率分别为3.43%与1.12%。

由此可知，本文方法在识别堆积型异常数据方面具有优势。

4 结论

以2 台机组的复杂异常数据为例，验证了本文方法的有效性。

（1）对风电机组运行数据进行分析与处理时，在水平功率方向上以一定功率间隔分层划分工况，采用非参数模型扩散核密度估计方法对各个水平功率区间运行数据进行概率分布估计，从而克服了KDE 带宽选取以及边界校正问题，提高了KDE 的局部适应性。

（2）利用参数模型混合威布尔分布拟合扩散核密度估计的概率密度曲线。模型参数p，α，β能够直观准确描述水平功率区间中数据整体分布特征，可依此准确判别水平功率区间中运行数据分布是否正常。

（3）采用平均置信区间异常数据清洗方法。对非正常水平功率区间，采用平均置信区间宽度确定识别异常数据的上下分位点，实现异常数据的准确识别与剔除。

在后续研究中，将对水平功率区间的划分间隔开展深入研究，力图在保证核密度估计效果的基础上给出区间划分依据，进一步提高异常数据识别的效果。