混流式喷水推进泵叶轮结构稳定性研究
覃小瑞,王名扬,徐增丙,林辉,王志刚
(1.湖北工业大学机械工程学院,湖北武汉 430068;2.武汉科技大学机械自动化学院,湖北武汉 430081;3.中国船舶工业集团公司,上海 200011)
0 前言
喷水推泵进以其机动性好、操作性优、高航速推进效率高、振动噪声小、抗空化能力强等特点在各国海军舰艇和民用船舶上得到广泛应用。叶轮作为其核心部件,在运行过程中除受重力、电机转矩作用外,还受到水力等外界激振力作用,容易使机组及叶轮等产生振动而造成严重事故。因此,对叶轮应力、变形以及模态进行有效分析很有必要。
国内外已有很多学者对潜水泵、轴流泵、水轮机及离心泵的结构稳定性进行了研究,但对于喷水推进泵叶轮结构稳定性研究则相对较少。吴刚等人对喷水推进轴流泵的叶轮受力情况进行了分析,并分别推导出了等环量和变环量设计下的强度校核公式,可供设计人员参考。董新国利用经验公式和流固耦合的方法计算了喷泵的动叶轮和导叶的静强度。李留洋等运用计算流体力学和有限元方法对混流式喷水推进泵叶轮强度进行了计算和分析,结果表明:叶片的最大变形量小于叶轮叶顶间隙,叶片的根部出现应力集中,叶片最大变形出现在叶片顶端导边处。单向流固耦合方法计算应力和变形已在工程界得到认可。
本文作者利用单向流固耦合的方法以某混流式喷水推进泵为研究对象,对喷水推进泵叶轮进行强度和振动特性预测。研究成果可为喷水推进泵运行稳定性和可靠性提供一定的理论参考。
1 计算模型及边界条件
1.1 流体域的建立及边界条件
本文研究的喷水推进泵计算流体域包括进出口延伸段、导叶及叶轮,喷水推进泵模型设计流量=2.53 m/s、设计扬程=25.6 m、转速=1 000 r/min、叶轮叶片数=6、导叶叶片数=11。采用ICEM网格划分软件对混流式喷水推进泵数值计算区域进行非结构网格划分,当网格数大于250×10时混流式喷水推进泵的扬程和效率受网格的变化影响较少(见表1)。全流域网格如图1所示。在进行流场计算时,选取SST湍流模型,进出口边界条件分别定义为质量流量进口和静压出口,壁面采用无滑移边界条件,叶轮与导叶以及叶轮与进口延伸段的交界面采用Stage(Mix-plane),并采用GGI网格技术拼接。
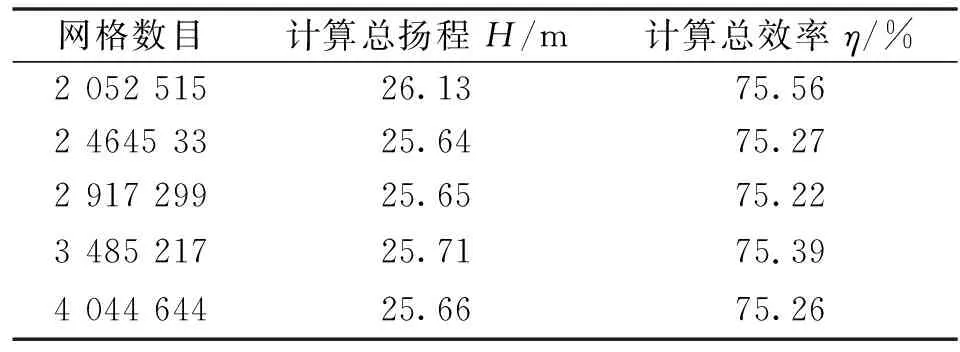
表1 网格无关性分析

图1 喷水推进泵全流道网格模型
通过对10种工况下混流式喷水推进泵的稳态数值模拟得到其性能曲线如图2所示,在设计工况下,混流式喷水推进泵效率达到最大值约为75%时对应的扬程为25.64 m。由图2可以看出,混流式喷水推进泵稳态数值模拟结果与泵的主要设计要求基本一致,因此该计算模型可以较准确预测推进泵的水力性能。
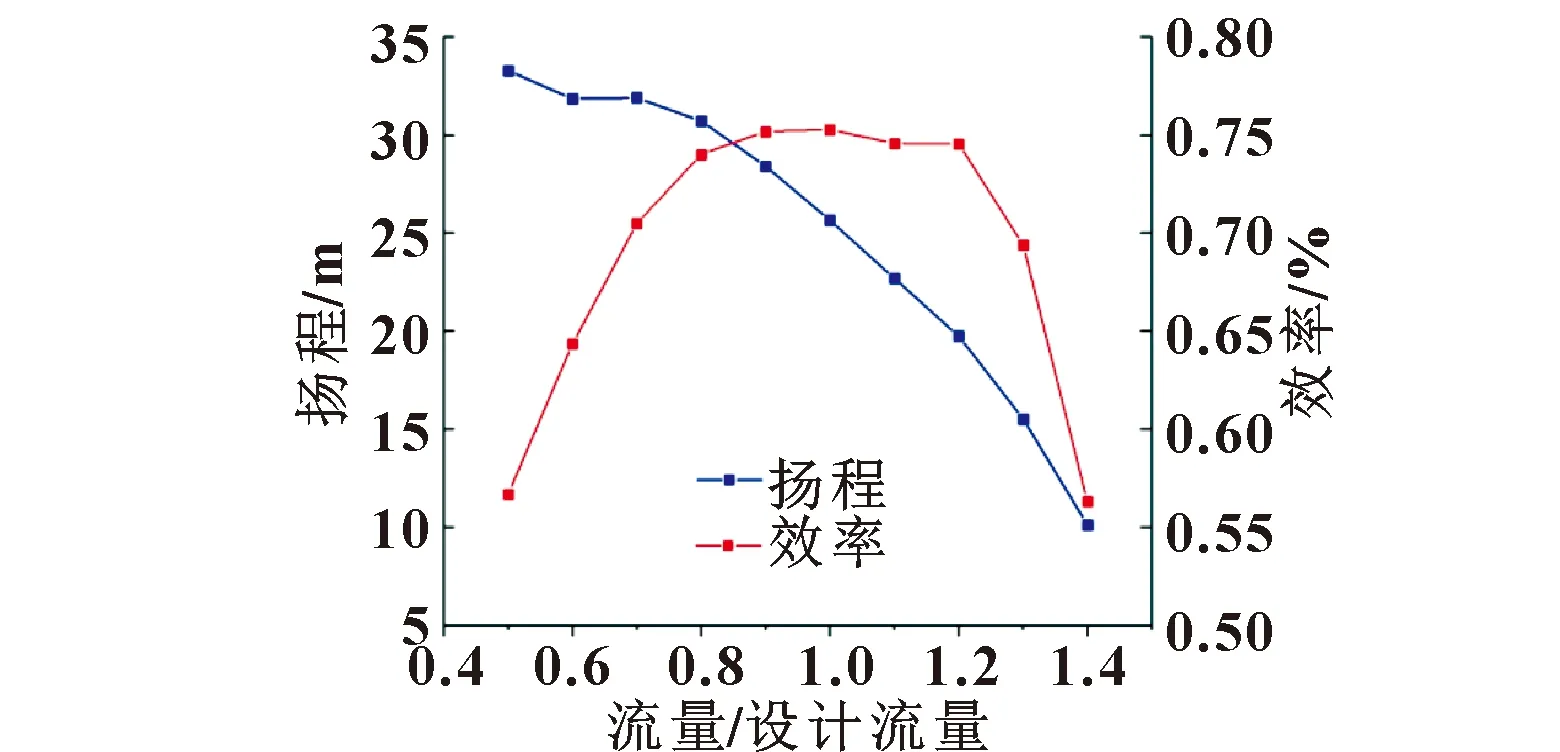
图2 混流式喷水推进泵外特性曲线
1.2 固体域的建立及边界条件
叶轮结构材料为双向不锈钢,其物性参数如表2所示。采用Workbench自动网格划分软件,对叶轮固体域进行非结构网格划分,经网格无关性验证,最终确定叶轮网格数为316 339、节点数为183 348,叶轮结构网格如图3所示。静力学计算和预应力模态计算时,叶轮与泵轴连接的位置设置为圆柱约束,约束径向、轴向及周向自由度;将叶轮自身重力、叶轮旋转产生的离心力加载到叶轮结构上;将CFD计算得到的不同工况下的流体载荷加载到叶轮表面,具体布置如图4所示。

表2 叶轮材料物性参数
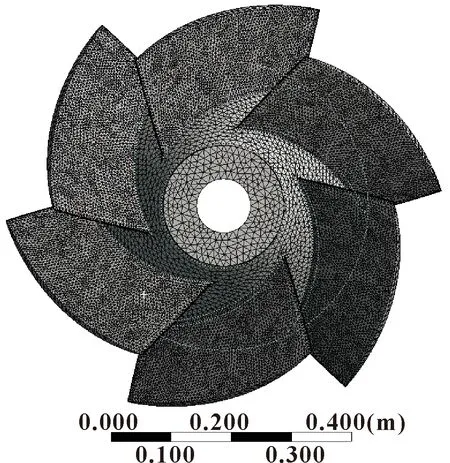
图3 叶轮固体结构网格模型
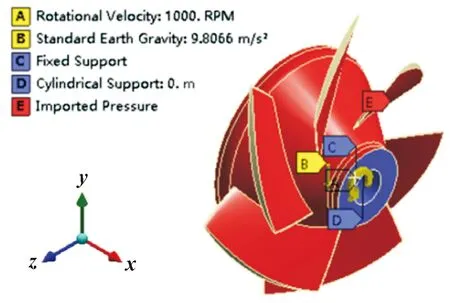
图4 叶轮结构载荷和约束
2 叶轮结构静力学分析
2.1 叶轮结构等效应力
为研究变流量工况下叶轮结构等效应力及等效应力随流量变化规律,基于单向流耦合方法,得到3种工况下等效应力云图。
稳定工况下,叶轮叶片所受应力主要包括:旋转时作用在叶片上的离心力所引起的拉应力,叶片越长、轮毂直径及转速越大,其拉应力越大;推进泵内部流场压力作用产生的弯曲应力;推进泵内部流场压力作用产生的扭应力。
图5所示为小流量工况(0.6)、标准工况(1.0)及大流量工况下(1.3),喷水推进泵叶轮等效应力分布图。可以看出:在小流量工况、设计工况及大流量工况下,推进泵叶轮背面及工作面的最大等效应力均发生在叶片根部,这是因为当叶轮发生振动时,在靠近轮毂位置无法通过弹性变形释放应力,从而在该位置出现应力集中,此处也是叶轮最容易出现裂纹及断裂的位置;叶轮叶片轮缘处应力相对较小,整个叶轮应力分布情况是以叶轮叶片靠近轮毂处为中心,向外递减;随着小流量向大流量的过渡,叶轮叶片各位置应力值都有所增大,其中大流量工况下最大等效应力为100.2 MPa,远小于材料的屈服强度550 MPa,并且最大等效应力位置也由叶片叶根中部逐渐转移至靠近叶轮出口的叶片根部位置;在同一工况下,叶轮叶片背面与工作面的应力分布情况相似,但应力大小有所变化。

图5 叶轮等效应力分布
2.2 叶轮结构变形
图6所示为小流量工况(0.6)、设计工况(1.0)及大流量工况(1.3)下,喷水推进泵叶轮位移变形分布图。可以看出:叶轮背面及工作面的最大位移均发生在靠近叶轮出口叶缘位置,这是由于叶轮叶片在靠近出口位置背面与工作面压差较大且叶轮叶缘厚度较薄,刚度不足。随着小流量向大流量的过渡,叶轮叶片变形梯度开始出现变化。小流量时,叶轮叶片位移变形由轮毂向轮缘逐渐增大;随着流量的不断增大,在大流量工况下,叶轮叶片变形由叶轮进口轮毂位置斜向叶轮出口轮缘位置逐渐增大。叶轮叶片最大变形位置逐渐集中在靠近叶轮出口叶缘位置,且最大变形值呈不断增大的趋势,其中大流量工况(1.3)下最大位移变形值约为0.75 mm,均满足叶轮结构稳定性变形量小于2 mm的要求;同一工况下,叶轮叶片背面与工作面的最大位移变形值在数值上略有不同。

图6 叶轮结构变形
3 叶轮结构模态分析
3.1 叶轮结构模态振型分析
为揭示叶轮结构在实际激励作用下变形规律,基于有限元方法,对叶轮结构模态振型进行求解分析。尽管不同类型的模态频率有所不同,但其振型基本相同,本文作者以干模态振型进行分析说明。由图7可知:第1、2阶振型相似,只是振动方向有所不同,主要表现为弯曲变形,最大变形发生在叶片外缘,且呈对称分布;第3阶振型表现为绕轴旋转,最大变形发生在叶轮外缘中间位置;第4、5阶振型相似,振动方向不同,主要表现为弯扭变形,最大变形发生在叶轮外缘靠近出水口位置;第6阶振型表现为绕轴的旋转,最大振型发生在叶轮外缘靠近出水口位置。

图7 干模态前6阶振型
3.2 叶轮结构固有频率分析
为探究变流量工况及变转速工况下叶轮结构振动特性,分别针对变流量3种工况下及变转速3种工况下叶轮结构进行模态分析。根据有无受外力作用,模态分析分为预应力和非预应力模态。从理论上讲,结构模态有无穷阶,但现实中振动主要由前6阶模态振型叠加而成。因此,文中重点探讨叶轮结构前6阶模态,其模态固有频率如表 3和表4所示。
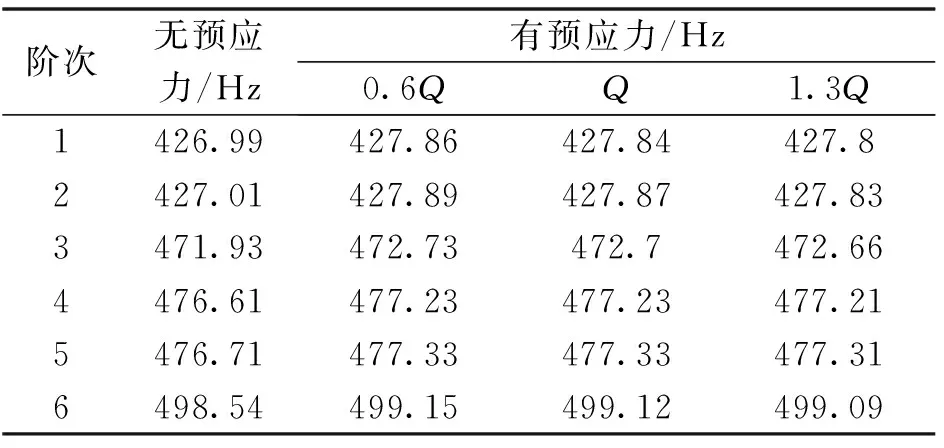
表3 流量预应力对叶轮结构固有频率的影响
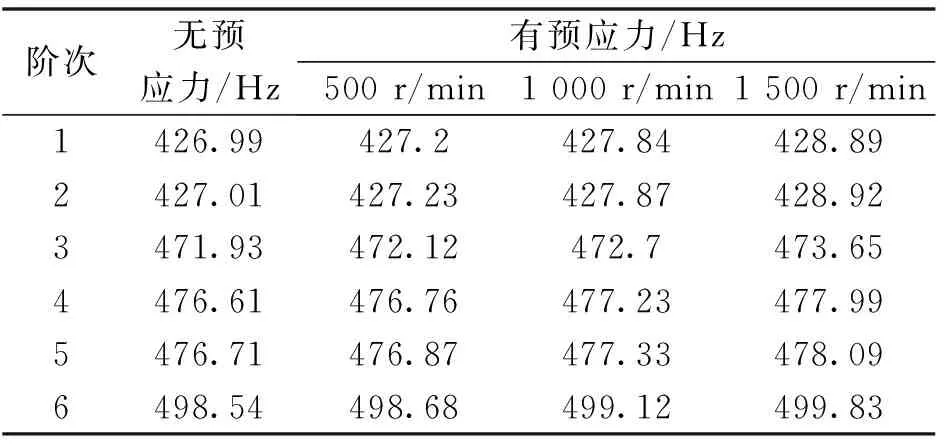
表4 转速预应力对叶轮结构固有频率的影响
由表3可知:叶轮结构随着阶数的增大其固有频率逐渐增大,且1阶与2阶、4阶与5阶固有频率相近,其原因是叶轮结构具有对称性,导致某相邻两阶固有频率相近。与无预应力情况相比,有预应力情况下叶轮结构的各阶固有频率有所增加。其重要原因是,叶轮结构受预应力影响下,叶轮结构受到流体作用力、自身重力及旋转产生的离心力,导致其结构刚度增大。流体作用力对于叶轮结构固有频率影响较小,由表3还可以看出:随着流量的增大,叶轮结构固有频率略有下降,其下降值为0.02~0.07 Hz,说明叶轮结构刚度相对较大,流体作用力使其刚化程度较低,可近似忽略。
由表4可知:对比不同转速下预应力模态频率,叶轮结构固有频率受转速影响较为明显,随着转速的增大,其各阶固有频率都有所提升,其增值为0.14~1.91 Hz,说明叶轮旋转产生的离心力提升了叶轮刚度,进而提高了其固有频率。
3.3 计算结构与叶轮特征频率比较
将叶轮的各阶固有频率与推进泵的特征频率作比较,以判断叶轮结构是否有发生共振的可能。
(1)喷水推进泵叶轮叶片旋转频率为
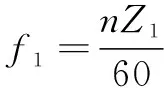
(1)
式中:为叶轮叶片通过频率,Hz;为转速,r/min;为叶轮叶片数。
(2)喷水推进泵导叶通过频率为

(2)
式中:为导叶通过频率,Hz;为转速,r/min;为导叶叶片数。
(3)典型激振力频率与叶轮固有频率对比分析
由上述公式可计算得到所研究喷水推进泵的叶轮叶片通过频率及导叶通过频率,如表5所示。对比表4和表5可知:变转速下激振频率远小于其对应的固有频率,频率之间相差较大,这3种变转速工况下叶轮的激振频率不会诱发叶轮结构共振,但需注意叶轮转速不易超过4 000 r/min,否则极容易诱发叶轮共振。

表5 变转速激振频率
4 结论
基于单向流固耦合方法,分别在变流量、变转速工况下,分析叶轮结构强度和振动。主要结论如下:
(1)在3种变流量工况下,推进泵叶轮背面及工作面的最大等效应力均发生在叶片根部,叶轮叶片轮缘处应力相对较小;随着小流量向大流量的过渡,叶轮叶片各位置应力都有所增大,其中大流量工况下最大等效应力为100.2 MPa,远小于材料的屈服强度。
(2)叶轮背面及工作面的最大位移均发生在靠近叶轮出口叶缘位置,随着小流量向大流量的过渡,最大变形值呈不断增大的趋势,其中大流量工况下最大变形约为0.75 mm,满足叶轮结构稳定性变形量要求。
(3)叶轮固有频率受流量变化影响较小,其下降值为0.02~0.07 Hz;相较于流量对叶轮结构的影响,转速的变化对叶轮结构影响较大,其增值为0.14~1.91 Hz。
(4)3种转速下激振频率都远小于叶轮结构的一阶固有频率,且频率之间相差较大,不会诱发叶轮结构共振,但需注意叶轮转速不易超过4 000 r/min,否则极容易诱发叶轮共振。

