桥梁检测中基于非结构化网格的时差菲涅尔带反演方法研究

邓 飞 聂焕鑫 沈联洪 李 旭 杨 林

(1.成都理工大学计算机与网络安全学院， 成都 610059； 2.成都交通投资集团有限公司， 成都 610041)

随着国家经济快速发展，我国在城市建设方面成效显著，诸多公路桥梁被不断建起。但人口数量的剧增给交通运输造成了很大压力，随着时间推移，在各种因素的影响下，桥梁结构会受到一定损伤。因此桥梁的检测工作对保障城市的正常交通运输和推动经济发展有着重要意义[1-2]。

桥梁检测作为一门逐渐兴起的学科，现有众多的检测技术，比如波动层析(CT)检测技术[3]、光纤传感检测技术[4]、探地雷达检测技术[5]，无人机检测技术等等[6-7]。其中波动CT检测技术是利用敲击产生的声波或振动波在工程介质中的传播特性，通过检波器采集穿过桥梁的波并用计算机加以分析，来探查桥梁内部结构的一种技术。由于其施工简便、检测结果直观可靠，可以直接反映桥梁内部的质量、缺陷与损伤等情况，成为了近年来桥梁无损检测的热点。

CT技术原为医学X射线的理论，后被用于地震层析中检测地下介质的结构情况。同理，也可用于桥梁检测中。徐蓉等将CT成像技术引入大型桥梁基桩的超声波检测中[8]，使检测结果更直观、异常圈定更准确；谷昊提出在桥梁检测中使用声波CT技术[9]，探讨了CT技术对桥梁混凝土检测的可行性；袁浩等将弹性波层析技术运用于桥梁无损检测[10]，实践结果较好地反映出了混凝土浇筑的质量情况；Li等研究了一种基于压缩采样的超声波层析技术[11]，进一步减少了测量工作量，可以较快速和精确地检测桥梁混凝土的缺陷部分。

在桥梁无损检测中，CT检测技术有分辨率高、可靠性好等特点，然而以上技术所采用的反演模型大多仍基于矩形网格，不适用于对不规则桥梁模型的反演计算[12]；且测量代价与工作量等依然较高，在桥梁检测工程中难以全面实施，无法拾取大量数据保证反演精度；此外也未考虑激发设备无法准确记录起振时间所造成的时差对小尺度的桥梁反演造成的影响。为此，本文提出一种基于非结构化网格的菲涅尔带层析反演算法，并结合时差法，通过理论模型与实地测量，验证了该方法在解决以上提出的桥梁检测问题上是可行性的。

1 方法原理

桥梁CT检测是通过激发振动波穿透混凝土，根据拾取的振动波走时计算出振动波在桥梁混凝土中的速度分布，从而对混凝土结构进行成像的技术。分为模型正演和层析反演两个部分，在正演过程中建立桥梁初始模型，使用正演算法计算振动波的理论走时和射线路径；在反演过程中用实际拾取的振动波初至数据与正演结果比较，利用反演算法对理论桥梁模型进行迭代修正，最终得出真实桥梁模型。

基于非结构化网格的时差菲涅尔带反演方法，是一种使用时差法拾取初至时、在SIRT反演算法上引入菲涅尔带的的桥梁层析检测方法。本方法的计算思路如图1所示，先建立初始桥梁模型和观测系统，其中桥梁模型的初始速度利用测量数据通过式(1)计算得到：

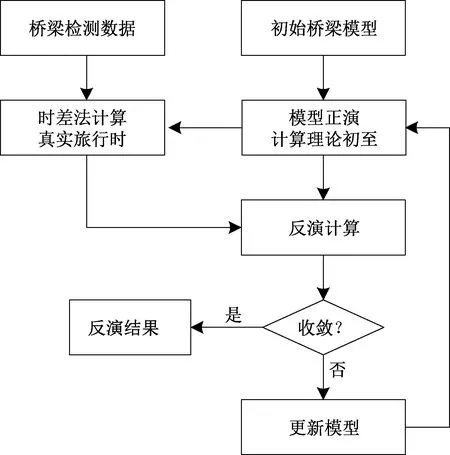
图1 反演流程Fig.1 Flow chart of tomography

v=(li-lj)/(ti-tj)

(1)

式中：li与lj为单炮中距离起振点最近的两道；ti与tj为对应的测量初至时。一般认为起振点近道桥梁质量良好，因此通过式(1)即可利用不准确的初至时计算出桥梁正常速度，为保证准确性，也可综合多炮数据取均值。

在建立好初始模型后，对模型进行正演计算理论初至；然后利用时差法计算出真实旅行时，将真实旅行时导入桥梁模型，利用基于菲涅尔带的SIRT反演算法对模型进行反演，并更新模型，重复该过程直至迭代结果满足终止条件，得到最终反演出的桥梁速度模型。

1.1 基于非结构化网格的正演

在地震层析成像中，常用的正演算法之一为旅行时线性插值法(Linear Travel Interpolation, LTI)，该算法以矩形网格剖分介质模型，利用最短路径算法，通过线性插值公式来向前和向后处理，可以计算出任意网格节点的旅行时。该方法最初用于地震勘探时，矩形网格对模型的划分仅在近地表不平处会产生一定的误差。然而在桥梁检测中，由于桥梁规模相对较小、边缘轮廓不规则，使用矩形网格划分会产生较大误差。

为提高反演结果的整体精确度，本文使用三角网格剖分桥梁模型，对比矩形网格，在相同网格密度下可以更好地贴合桥梁边缘，因此在正演过程中也需要使用基于非结构化网格的LTI算法[13]，减小了正演射线误差，配合本文基于三角网格的反演算法，使桥梁层析总体结果的精度得到了提升。反演算法及初至拾取将在1.2、1.3节中介绍。

1.2 菲涅尔带反演方法

联合迭代重建技术(Simultaneous Iterative Reconstruction Techniques, SIRT)是射线旅行时层析反演的常用方法之一[14]。本文使用的三角网格模型与矩形网格模型在计算上类似，即：

(2)

式中：Sj为第j个三角网格的慢度；q为迭代次数；Nj为穿过网格j的射线数目；ΔSjn为穿过网格j的第n条射线对网格j的慢度修改量。

在地震层析反演中，使用了大量检波设备来采集初至数据，大量数据的支持使得射线SIRT算法反演出的结果具有较高的精确度，然而在桥梁CT检测中，受经费、施工条件等因素制约，检波设备不足，导致射线稀疏，模型覆盖面积小；此外，射线只是地震波的高频近似，不能反映真实的物理过程，会对反演准确性造成较大影响。

为解决上述问题，本文引入了菲涅尔带层析反演方法[15]。由于振动波能量在现实中是沿着数学射线菲涅尔带范围内的介质传播的，因此在反演过程中加入菲涅尔带，不仅更能反映振动波的真实传播情况，也能扩大射线的覆盖范围，如图2所示。

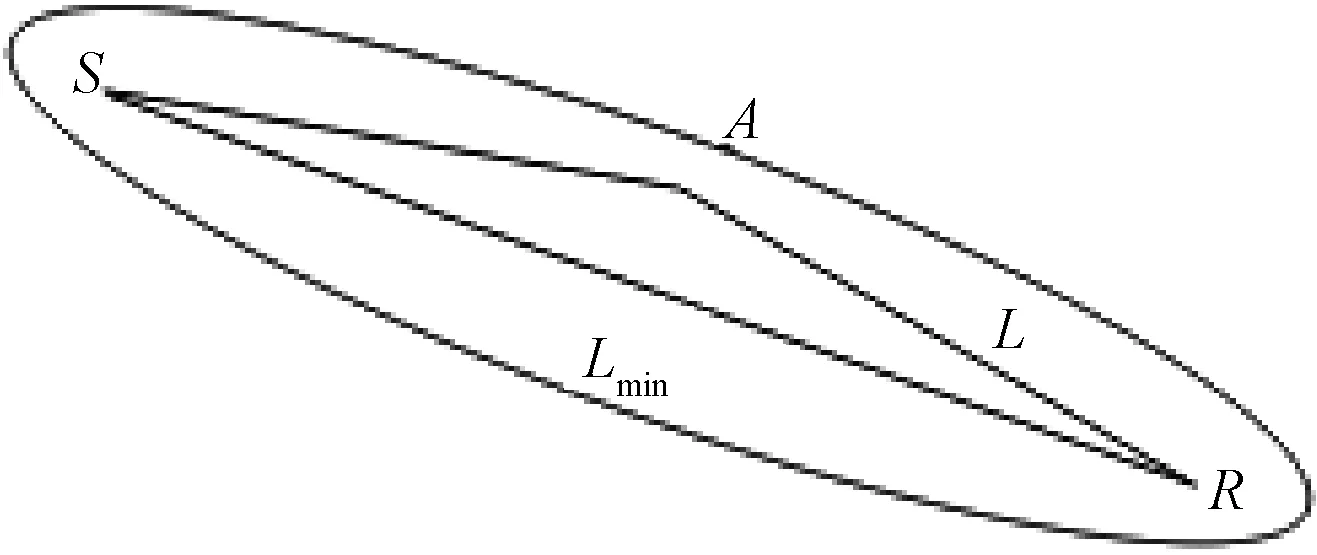
图2 菲涅尔带示意Fig.2 The schematic diagram of Fresnel zone

S为炮点，R为检波点，椭圆条带为射线SR的菲涅尔带。A为模型内任意点，根据射线追踪法可以计算出S到A的旅行时t(S,A)，又根据振动波传播的互异性，可计算出A到R的旅行时即为t(R,A)。由此可以得出菲涅尔带范围判定式：

|t(S,A)+t(R,A)-t(S,R)|≤1/2f

(3)

式中：t(S,R)即为射线旅行时；f为菲涅尔带频率。

根据式(4)可以计算出模型中任意三角网格是否处于射线菲涅尔带范围内。

综上所述，本文提出的三角网菲涅尔带时差层析反演算法步骤如下：

1)建立桥梁模型，对桥梁模型进行三角剖分，在模型中布设炮点和检波点；

2)给定初始慢度S0；

3)设定总迭代次数N，设定反演终止的平均误差门槛值ξ0；

4)将三角网格的累计慢度修改量设为零；

5)遍历每个炮点开始反演计算；

6)通过正演计算得到第i个炮点到每个检波点的旅行时表和射线轨迹，使用时差法对拾取的初至波的旅行时进行计算，得到合成后的旅行时；

7)找出每根射线菲涅尔带范围内的三角网格，加入表L中；

8)计算表L中每个三角网格的慢度修改量，并累加慢度修改量；

9)重复步骤5)～8)，完成炮点循环，使用累计慢度修改量修改模型；

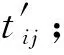
11)使用评价函数：

(4)

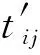
12)重复步骤4)～11)，直到满足ξ<ξ0或迭代次数大于N，退出迭代，反演计算完成。

对于菲涅尔带的范围大小，由于桥梁体积相对较小，使菲涅尔带频率f=2 000 Hz进行测量效果较为理想，在上述反演迭代的步骤7)～8)中，需找出射线菲涅尔带范围内的三角网格，并对其慢度进行修正，具体步骤如下：

1)要找出射线的菲涅尔带范围内的所有三角网格，先要找出当前射线通过的三角网格，每条射线由多个节点连接而成，为此先建立一条队列Q；

2)遍历射线的每个节点，得到节点所在的三角网格，将其加入队列Q，并标记为菲涅尔带范围内的三角网格，下述简称为加上flag标记，每条射线的flag值不同6，并加入表L当中，这些射线直接通过的三角网格的权值Ω=1；

5)判断队列Q是否为空，如果不为空，重复步骤4)，如果队列Q为空，说明当前射线菲涅尔带范围内的三角网格已经被全部找出并加入表L中，开始下一步计算；

6)遍历表L中的每个三角网格，将每个网格的权值Ω除以表L中所有三角网格的总权值，得到当前三角网格的权重百分比Ω，则当前三角网格的慢度修改量ΔS=Ω·Δt；

7)表L的所有三角网格计算完毕后，当前射线便计算完成。

1.3 时差法

由于微振层析技术无法准确记录起振时间[16-17]，单炮记录的各道初至时间与真实旅行时之间存在相同的毫秒级误差，导致拾取的初至数据不准确。因此本文提出了基于时差的反演方法，在拾取的初至数据不准确的情况下，将初至数据通过计算化为近似真实的旅行时，可以取得与使用准确数据近似的反演效果。

时差法取距离起振点最近的检波点作为参考，认为该检波道途经的桥梁质量良好，其真实旅行时应该与初始模型正演计算出的射线旅行时近似，因此该道在实际中拾取的初至时间与正演旅行时之差即为该炮的时差。单炮第j道的真实旅行时计算如下：

(5)

使用式(5)对实际初至数据进行处理后，代入反演计算可以得到较为准确的反演结果。

2 模型试算与实测

2.1 梁柱模型试算

首先在简单矩形梁柱模型上初步测试菲涅尔带方法的反演效果，建立10 m×2 m的梁柱初始模型(图3a)，设置振动波在模型中传播的速度为3 000 m/s，在梁柱两边以1 m为间隔布设检波点(图3b中蓝点)，并在内部设置三列炮点(图3b中黄点)，先后在高8 m处的梁柱中设置1 m宽、2 000 m/s(图3c)，1 m宽、1 000 m/s(图3e)和0.1 m宽、1 000 m/s(图3g)的低速区。分别对模型进行正演并将正演结果代入初始模型中，使用菲涅尔带反演法反演迭代30轮，得到相应反演结果。

根据图3d和图3f可以看出，2 000 m/s和1 000 m/s的1 m低速区模型反演结果的宽度约为1 m左右，接近于原模型，在区域边缘处存在模型1/10左右大小的降速区。对比图3h则发现，当低速区宽度为0.1 m，仅占整体梁柱模型1%的情况下，依然能在8 m高处反演出一片低速区，宽度在0.1 ～0.3 m之间，但对速度大小的反映略为不准确，此外在区域边缘处同样存在1/10左右的降速区。据此可以发现，随着低速区域的缩小，对低速区的大小和速度的反演精确度逐渐降低，但仍然能够检测出速度异常区域，因此合理设计观测系统、控制好模型与裂缝的比例，即可对不同大小的裂缝进行精确反演。

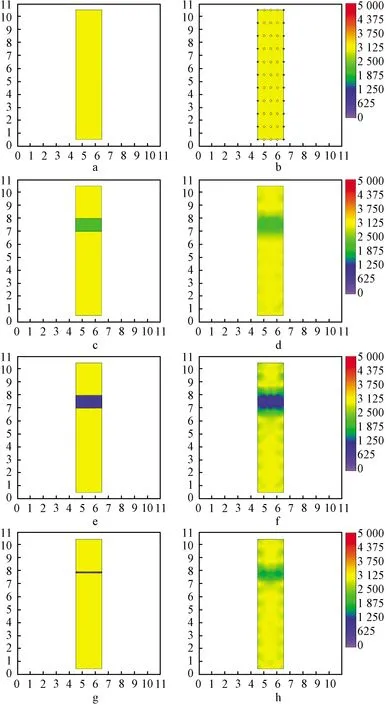
a—反演初始模型； b—点位布设；c—1 m宽、2 000 m/s低速区； d—图3c的反演结果；e—1 m宽、1 000 m/s低速区； f—图3e的反演结果；g—0.1 m宽、1 000 m/s低速区； h—图3g的反演结果。图3 理论梁柱模型试验结果Fig.3 Test resules of theoretical beam-column model

2.2 桥梁模型试算

下面在桥梁模型上检验本文方法的可行性，并与其他方法进行对比。建立最大宽高10 m的桥梁模型，设置振动波在模型中传播的速度为3 000 m/s，在桥梁边缘轮廓布设24个检波点(图4a中蓝点)，并在各处布设炮点(图4a中黄点)，在桥梁左侧和底部设置两处低速区，分别为1 000 m/s和500 m/s。对图4a的模型进行正演，将正演结果代入图4b的反演初始模型中，分别使用常规SIRT反演法和菲涅尔带反演法反演迭代30轮，得到的反演结果如图4c和图4d所示，对比两图发现，常规射线SIRT方法无法正确反演出速度异常区，而菲涅尔带SIRT方法的反演结果较准确地揭示出了低速区的形状与速度，能够较好地反映出速度异常区的形状和大小。

a—观测系统模型； b—反演初始模型；c—射线SIRT迭代30轮； d—菲涅尔带SIRT迭代30轮；e—扰动数据迭代30轮； f—时差菲涅尔带迭代30轮。图4 理论桥梁模型试验结果Fig.4 Test results of theoretical bridge model

图4e为对模型正演旅行时数据进行扰动后(分别随机地对每炮的各道旅行时数据进行统一的毫秒级改动)，使用菲涅尔带方法反演的结果，可以看出反演结果混乱，无法分辨速度异常区，说明无法准确记录起振时间对桥梁反演会造成较大影响。对扰动数据使用时差法并进行菲涅尔带反演迭代30轮的结果见图4f，对比图4d，发现使用时差法对扰动数据修正后的反演效果与使用准确旅行时数据的反演效果近似，说明时差法能够改善无法准确记录初至时间的问题。

图5为反演标准化残差，由于扰动数据的标准化残差为其余数据的十数倍，且下降速度较慢，因此未添加于图中。可以看到，随着迭代次数增加，标准化残差在不断减小，菲涅尔带方法的标准化残差相比SIRT方法减小了1/2左右，而对扰动数据使用时差法后，反演标准化残差也接近于菲涅尔带法。

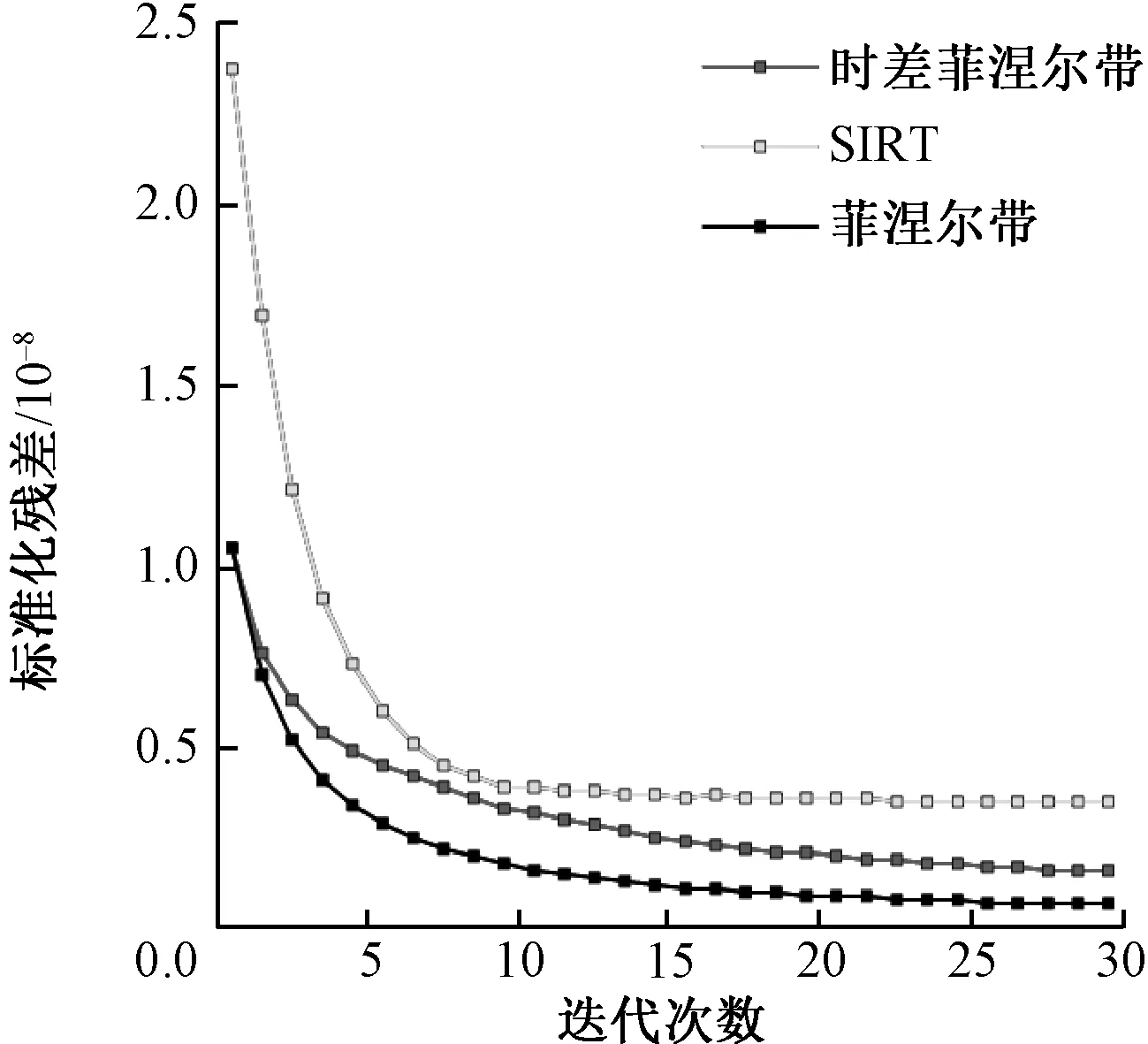
图5 反演标准化残差Fig.5 Standardized residual of inversion

2.3 实测数据处理

理论验证完毕后，开始实地测量，并对采集到的数据进行处理。数据采集在一块带有裂缝的水泥路面上进行，以裂缝为中心，选取长宽为5 m的区域。点位布设如图6所示，在区域两侧边缘以0.5 m间隔布设22处检波点，左下角为1号点，右下角为22号点。区域内以1 m为间隔设置4列共24处炮点(区域内标记处)，在炮点处用铁锤砸击铁饼，各检波点即能接受到振动波并将数据反馈至工程探测仪。

图6 现场施工照片Fig.6 The photo of site operation

图7为采集的振动波初至波形，从近炮道开始，拾取近炮道波形顶部对应的时间，并依次拾取后续道的初至(图7中红线)，即得到当前炮各道对应的初至。

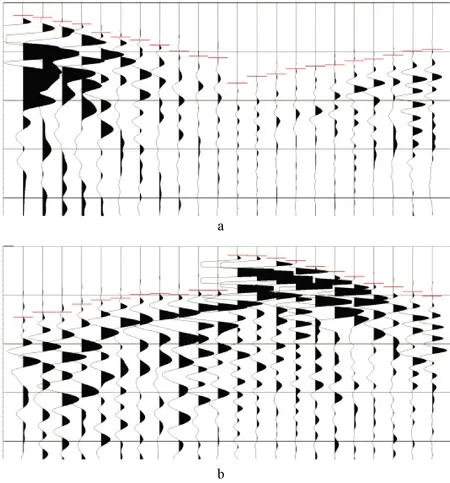
a—第1炮记录； b—第24炮记录。图7 初至波波形Fig.7 Oscillogram of first arrival

初至拾取完毕后，建立如图8a 所示的初始模型。利用式(1)对水泥路面的速度计算得出大致速度为2 650 m/s，并写入初始模型中。随后使用时差法对初至数据进行处理，并代入初始模型中进行反演计算。

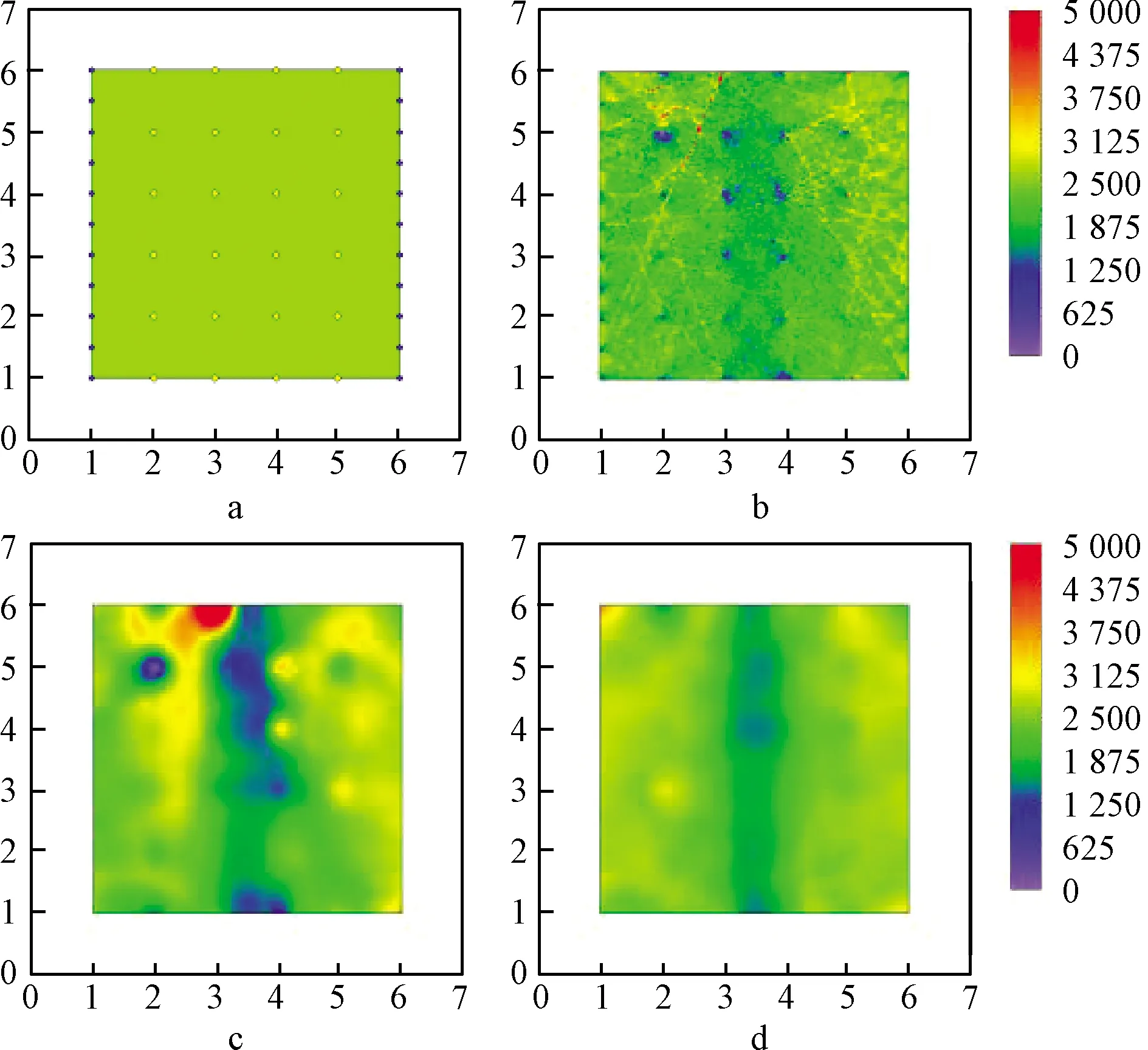
a—观测系统反演初始模型； b—射线SIRT反演效果；c—菲涅尔带SIRT反演效果； d—时差菲涅尔带反演效果。图8 实测反演结果Fig.8 Inversion results of actual measurement

图8b为使用拾取的原始初至数据，并使用常规SIRT算法对初始模型反演迭代20次的结果，图8c和图8d分别为菲涅尔带方法和时差菲涅尔带方法迭代20次的结果。可以看出：由于射线不够密集，图8b中SIRT方法对模型速度的修改主要集中于炮点及检波点附近，无法辨认速度异常区的形状。根据图8c可以看出，在模型中央存在带状低速区，但由于拾取的数据存在误差，模型反演结果的左上部存在明显的大范围高速区及小部分低速区，与测量地实际情况不符。而反观图8d，在对拾取数据使用时差法处理后，使用菲涅尔带方法反演的结果未对其余区域过度修正，较准确地反映出了模型中央的裂缝。

图9为实测数据反演迭代过程中的标准化残差，可以看出：在不使用时差法的情况下，反演标准化残差相对较大，菲涅尔带方法的残差曲线优于常规SIRT方法，而时差菲涅尔带法的标准化残差则远小于以上二者，并且从图8的反演效果也可以看出，时差菲涅尔带法在对实际模型的修正上同样能取得良好效果。

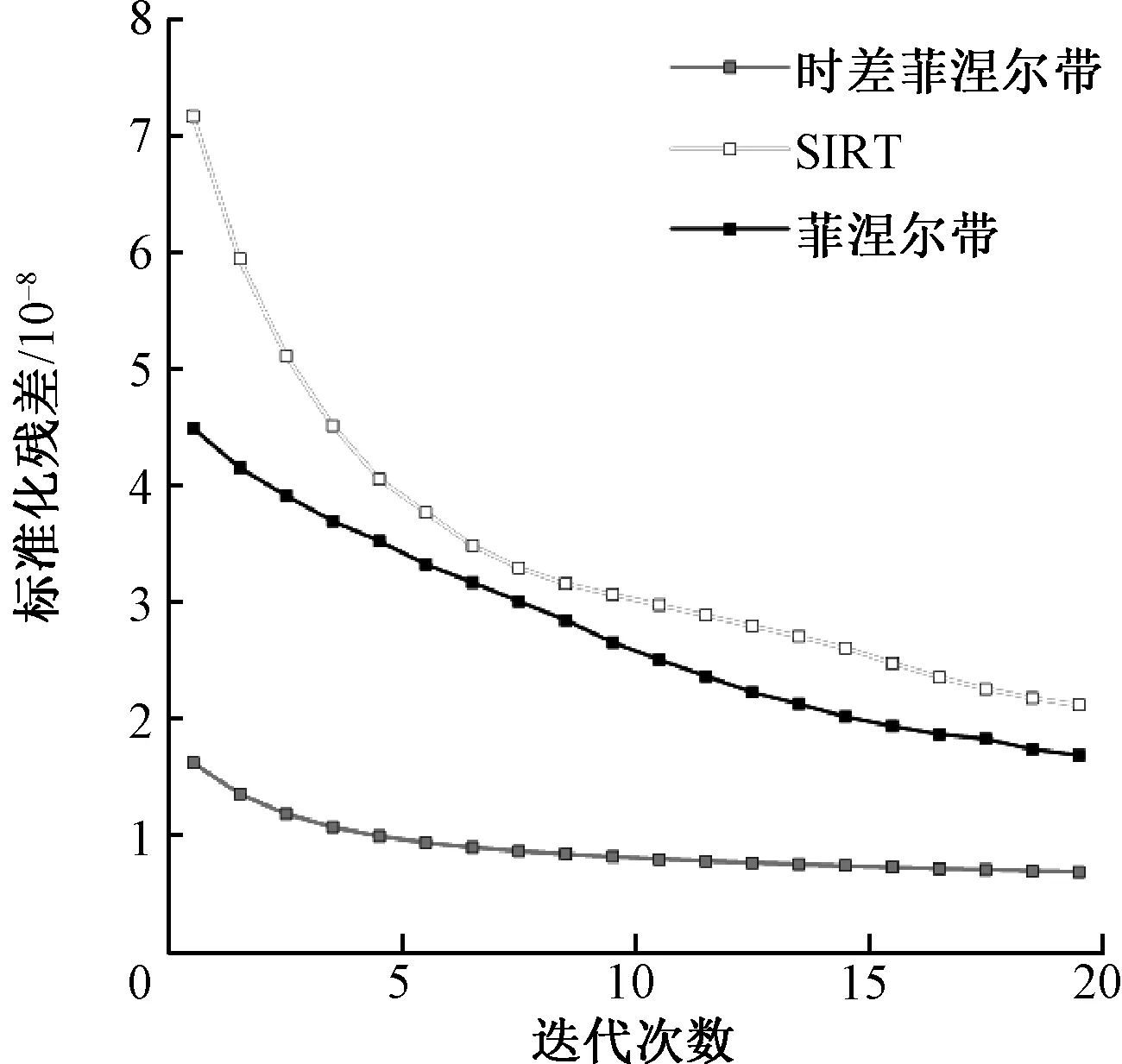
图9 实测标准化残差Fig.9 Standardized residual of actual measurement

3 结 论

利用基于三角网的时差菲涅尔带反演方法，分别对理论数据和实际测量数据进行了反演计算，通过对比常规SIRT方法、菲涅尔带方法以及时差菲涅尔带方法的反演结果，得到以下结论：

1)针对桥梁检测提出的基于三角网的时差菲涅尔带反演方法，通过对模拟梁柱模型、桥梁模型和实际测量数据的计算，证明了该方法在建筑结构梁、柱与桥梁检测领域的可行性。

2)理论试验和实际测量结果表明，菲涅尔带方法在检波点较少的情况下也能够对模型进行较正确的反演，而时差法则可以有效减小初至时间记录不准确造成的误差。基于三角网的时差菲涅尔带反演方法，对比常规射线SIRT方法，在对模型形状和速度的反演效果上有明显改善，可以应用于实际桥梁检测工程中。