装配式结构和自复位结构结合技术的设计方法
葛元辉 李延昌 韩良君 李 军 梁家栋 王荣棋 查晓雄
(1.中铁建设集团南方工程有限公司, 广东深圳 511400; 2.深圳市特区建工科工集团有限公司广东深圳 518034; 3.哈尔滨工业大学(深圳) 土木工程与环境工程学院, 广东深圳 518055)
0 引 言
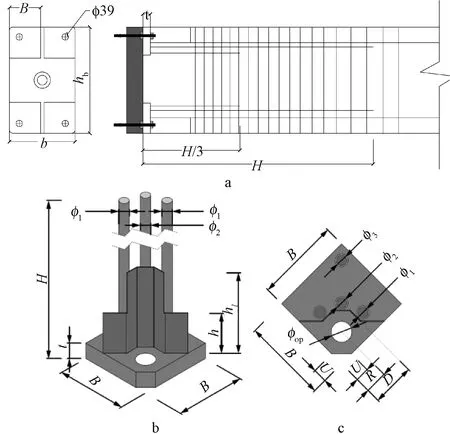
装配式连接形式主要有干连接和湿连接两种,干连接中的螺栓连接,可以快速完成柱脚节点、梁柱节点的连接,具备用工量少、施工高效等优点。国内外研究[1-3]表明,自复位结构通过施加预应力,结构在地震时发生摇摆,地震后基本无残余变形,且可快速修复投入使用。因此,在螺栓连接的基础上,本文结合自复位节点的特点,在梁截面中间预留孔洞,用于穿插无黏结预应力筋;在梁靴的背部放置螺母,使螺栓与梁靴协同运动,在地震下共同变形;在节点接缝处灌浆,此时螺栓杆部分无黏结,利用其拉压屈服来消耗地震能量;最后张拉无黏结预应力筋,从而形成基于自复位的装配式干连接节点(简称“干连接自复位节点”),如图1所示。
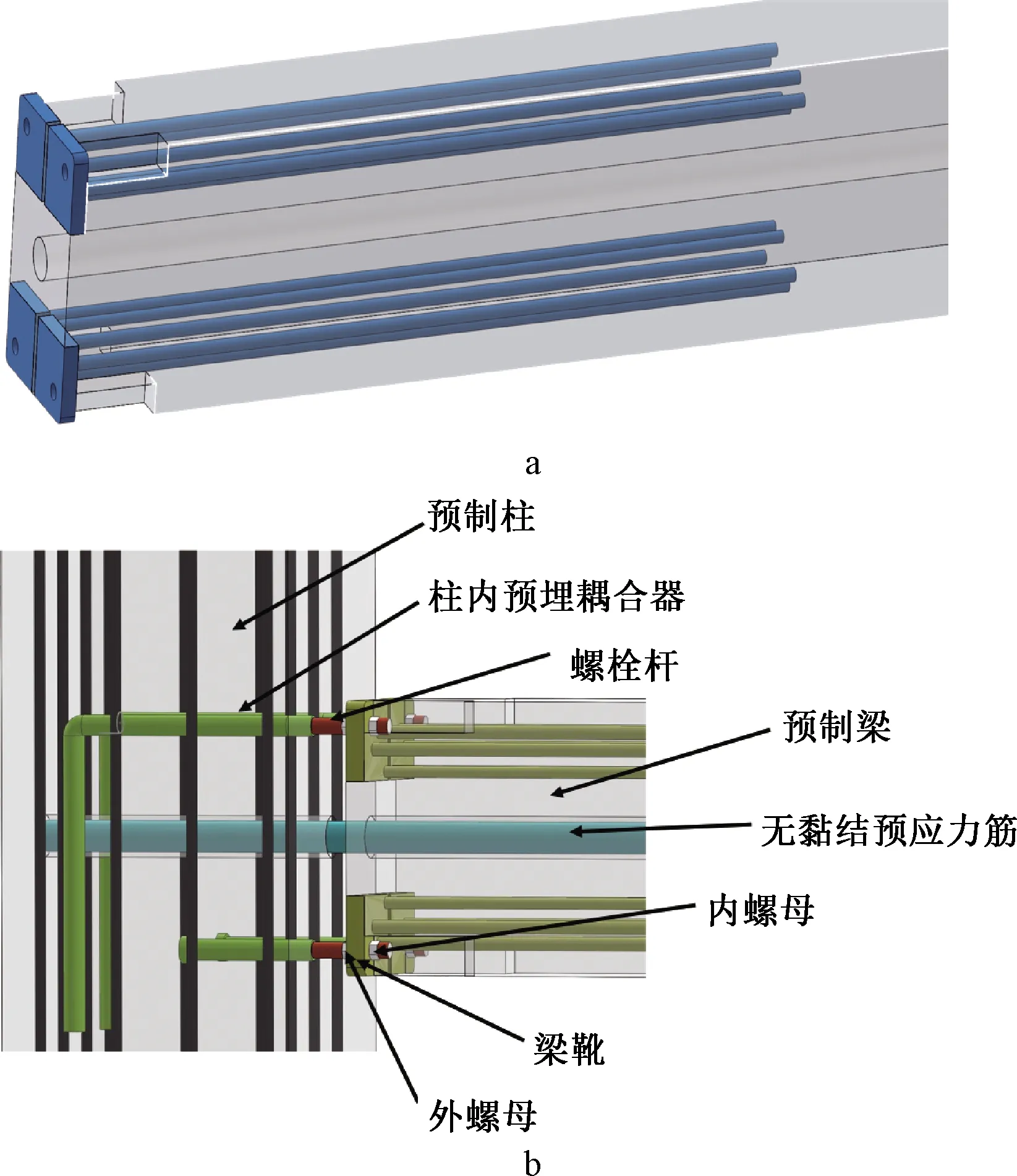
a—梁侧立面; b—正立面。图1 干连接自复位节点Fig.1 Dry-connection self-resetting joint
根据该干连接自复位节点,提出一种装配式结构和自复位结构相结合的设计方法,采用ABAQUS进行节点性能有限元分析,验证该设计方法的准确性。
新型节点既具备螺栓连接在施工上的优势,也具备了自复位连接在结构性能上的优势。梁柱构件在工厂预制完成,提高施工效率;在预应力作用下,梁柱之间产生夹紧力,夹紧力产生的贴合面摩擦力、螺栓的销栓作用和后续灌浆共同抵抗剪力,因此可以不用设置牛腿,降低施工成本;同时,采用螺栓连接,在罕遇地震后,只需更换螺栓,结构即可投入正常使用,达到“大震可修”的目标。
施工现场的施工顺序为:首先将梁柱的孔洞对齐,4个外螺母分别放置在梁靴外部,接着将螺栓杆包裹塑料或涂油的方式插入到梁靴孔洞中(形成无黏结段),旋转螺栓,插入柱中,在梁靴内部放置螺母并拧紧外螺母与内螺母,使得梁靴相对螺栓杆位置固定,保证地震作用时,螺栓杆实现拉压屈服耗能。最后在接缝处灌浆,并张拉无黏结预应力筋。
1 梁端受力、变形理论分析
与传统的现浇混凝土梁柱节点相比,干连接自复位梁柱节点的变形和耗能集中在梁端,在一定程度上可以减轻节点处混凝土的塑性损伤,因此针对梁端受力,变形、耗能及力-位移曲线等特性进行分析。
1.1 梁端轴力、剪力与弯矩的表达式
以节点承受负弯矩(顺时针)时的情况为例,进行隔离体分析。如图2所示,在外荷载作用下,梁端的反力包括上下螺栓提供的拉压力Nt、Nc,预应力钢绞线提供的压力P,梁柱接触面上摩擦力Ff,以及混凝土受的压力Fc。Ff可以表示为:
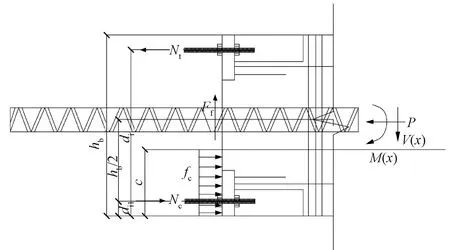
图2 节点隔离体示意Fig.2 The schematic diagram of joint isolator
Ff=μP
(1)
式中:μ为混凝土梁柱间的静摩擦因数。
根据图2中水平力的平衡关系可得:
Nc+Fc=P+Nt
(2)
同理,根据梁在竖直方向上的平衡关系可得:
Ff=V(x)
(3)
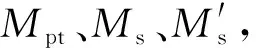
Nt(di-a/2)+Nc(di1-c/2)
(4)
式中:hb为梁截面高度;a为梁截面中性轴高度c与等效矩形应力系数β的乘积;di为受拉螺栓到受压混凝土翼缘的距离;di1为受压螺栓到受压混凝土翼缘的距离。
1.2 梁端力-位移关系
基本的弹塑性材料的滞回曲线形状如图3a所示:从原点开始受拉,到C点代表受拉屈服。随着外荷载减小到零时,对应图3a的F点,此时材料产生了残余变形。但如果一开始就让其受压屈服,再进行滞回加载,则得到的滞回曲线如图3b所示,相当于将原来的滞回曲线平移到第一象限。图3b中的AB段对应图3a中的AB段,材料的压力逐渐减小到E点(为零),在图3a中AB段的外力为压力,但在图3b中,由于存在初始压应力,所以AE段外力为拉力,但实际上材料此时仍然受压,EB段材料的内力由压力变为拉力,BC段为材料屈服段,CD段材料的内力由拉力转化为压力,DA段为材料受压屈服。对于图3a,在全部撤去外力F后,材料存在一定的残余变形,但对于图3b,在撤去外力后,能够在压力作用下恢复到压缩屈服状态,表现为外力撤除时,材料的位移也为零,即材料的屈服状态对应构件的初始状态,在构件层面就是没有残余变形,这就是自复位节点的基本工作原理。

a—弹塑性材料的滞回曲线; b—平移后弹塑性材料的滞回曲线。图3 两种不同的滞回曲线Fig.3 Two different types of hysteresis curves
本文的干连接自复位节点,如果螺栓在有预应力的情况下放置,由于存在灌浆料,在最初的弹性循环中,螺栓的应力可以忽略不计。然而,当一侧的螺栓在拉力下屈服,那么钢筋在节点关闭(回复到原位置)时总会有残余压应力,这是由钢的本构关系决定的,连接的转动越大,残余压应力越大,极限是钢材压缩时的屈服应力。对于所有的后续循环,在连接关闭阶段,螺栓始终处于压缩屈服状态,会有阻碍节点关闭的趋势,与后张预应力提供的恢复力方向相反。因此,对于螺栓受压屈服荷载与后张预应力的大小限制是:后张拉力产生的闭合力矩必须不小于压缩屈服时螺栓产生的力矩,确保连接件在外力去掉后,保证梁柱界面闭合,为抗剪承载力提供摩擦力。
对于最初螺栓未屈服的加卸载循环会有不同的消压力矩,在之后的自复位节点的力-位移关系中,忽略第一次加卸载循环所需要的特殊力-位移关系,使用螺栓开始完全屈服时的力-位移关系。在第一次循环荷载下,当上翼缘混凝土的Fc=0时,此时的弯矩称为消压弯矩Mdec,initial。连接处的消压点是指最外层纤维的应力等于零时的变形,此时的Mdec,initial与式(5)有关。
(5)
式中:Tpt,initial为预应力钢绞线总后张预应力;Z为梁截面模量;A为梁截面面积;e为从截面质心到后张预应力筋质心的距离,当后张预应力筋位于截面形心处时,e=0。
对于本文的干连接自复位节点,从第二次加卸载循环开始,自复位干连接节点的力-位移曲线如图4所示。同时采用Mole的分析结果[4]:为便于分析,节点部件可以用理想化的元素来表示,如理想的线性弹簧、摩擦块和放在上面的砝码,将节点等效为弹簧质量模型。图5为自复位干连接节点的等效弹簧质量模型,通过等效弹簧质量模型来模拟干连接自复位节点的力和位移关系。图中,构件的等效刚度为Kb;节点中的螺栓和后张预应力的刚度分别为Km和Kp;Mpe表示当连接首次打开时,由于后张预应力张力作用而产生的夹紧力矩;Mmy表示节点打开时螺栓的屈服弯矩。实际情况下,节点是转动节点,但为了简单起见,这里将其等效为平移模型。
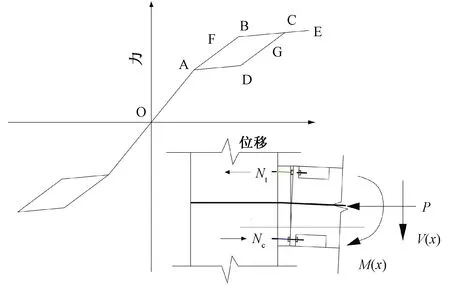
图4 干连接自复位节点滞回曲线Fig.4 Hysteresis curve of dry-connection self-resetting joint
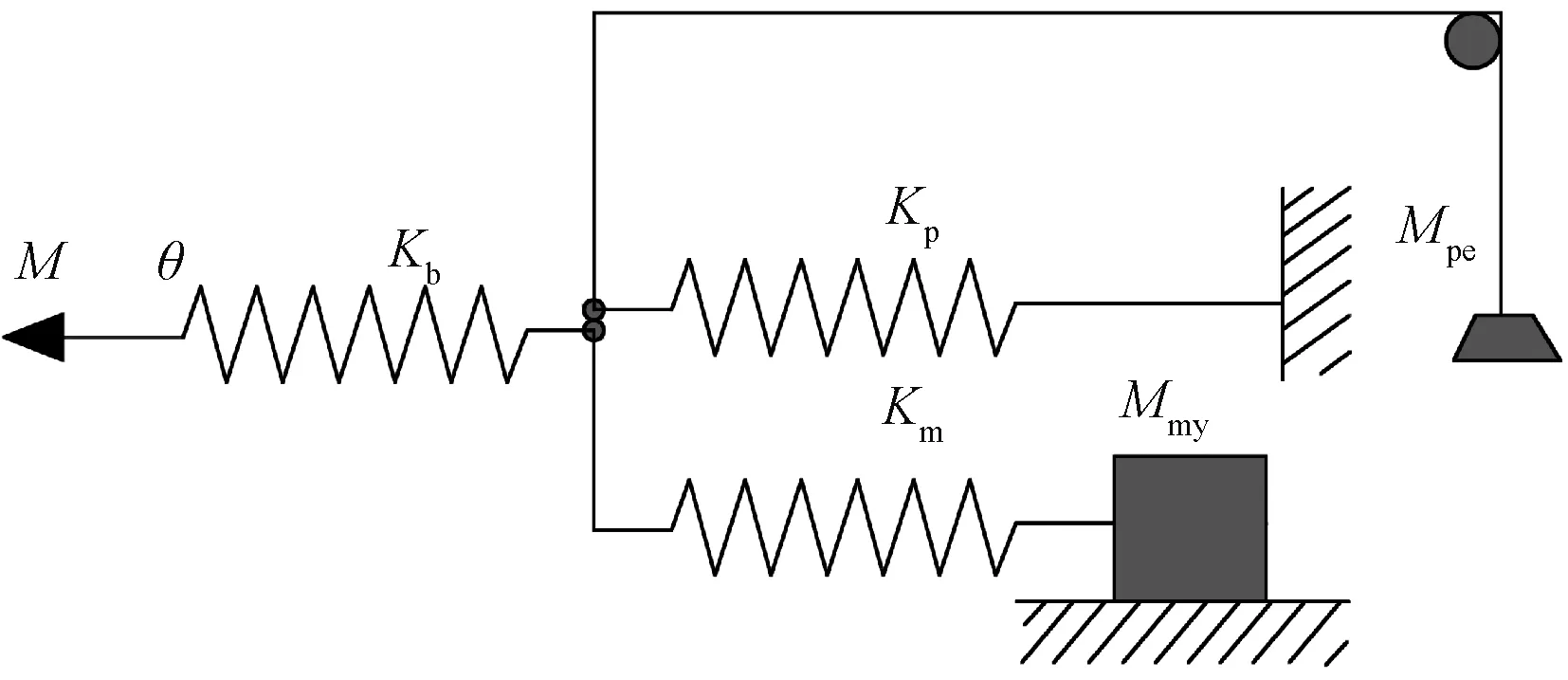
图5 等效弹簧质量模型Fig.5 Equivalent spring mass model
在第一个加卸载循环中,后张预应力张力作用产生的夹紧力矩Mpe是系统中唯一的剩余力矩,因此在连接处施加的力矩必须大于连接打开时的夹紧力矩。在连接打开之前,系统的刚度由梁和柱贡献。一旦连接打开,螺栓和后张预应力筋都提供弹性阻力,直到螺栓屈服。从这一点出发,假设屈服的螺栓具有零刚度(摩擦块不允许作用于螺栓的力矩高于Mmy,否则摩擦块将会相对滑动),在反向运动时,螺栓再次产生弹性阻力,直到压缩时屈服。该条件设定了一个设计极限,因为后张拉预应力应始终能够关闭连接,以抵抗螺栓在压缩屈服时的阻力(后张预应力保证梁柱贴合面之间的摩擦接触,以提供抗剪承载力),如式(6)。
Mpe≥Mmy
(6)
Mole只对模型进行上述简单介绍,并没有对等效质量模型的运动过程详细分析[4]。下文对其节点张开闭合的过程进行具体分析,将模型的运动过程与节点的力-位移曲线联系起来:默认Kp弹簧只能受拉变形,受压时视为刚体。因为在实际梁柱节点的变形中预应力筋张拉完,理想情况下变形后的应变都大于张拉应变。
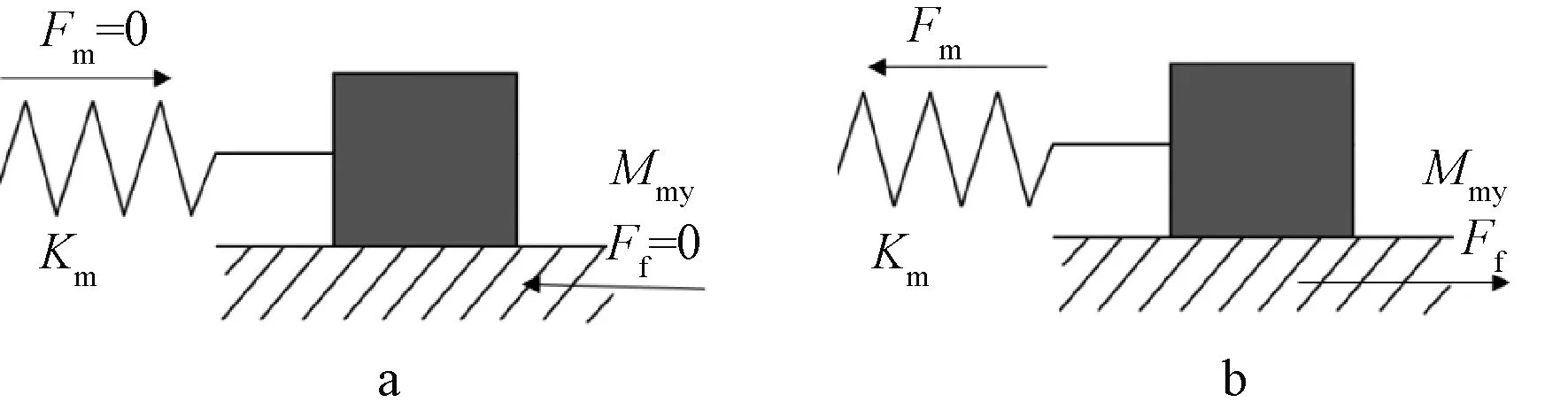
第一次加载:随着外力M增大,由于有Mpe的存在,开始只是弹簧的拉长,这个阶段对应节点首次张开前的消压作用,当M=Mpe时,梁端完全消压,此时的M=Mdec,initial;当M>Mpe时,整体由于产生向左运动的趋势,所以地面会给摩擦块一个向右的摩擦力,该阶段对应第一次循环节点打开到螺栓从零到受拉屈服这一阶段。此时采取隔离法分析,摩擦块由于受到向右的摩擦力,弹簧需要提供向左的弹力来维持整体平衡,如图6所示。此时弹簧(对应Km和Kb)都会伸长,对应预应力筋和螺栓都提供抗弯刚度。当外力M超过Mpe与Mmy之和时,对于摩擦块来说,外力超过其最大静摩擦,将会开始产生滑动,此阶段对应滞回曲线BC阶段,表示螺栓开始受拉屈服,提供的抗弯刚度不再增加,此时只有无黏结预应力筋提供抗弯刚度。

图6 第一次节点张开隔离体受力Fig.6 The force diagram of the isolator when the joints were opened for the first time
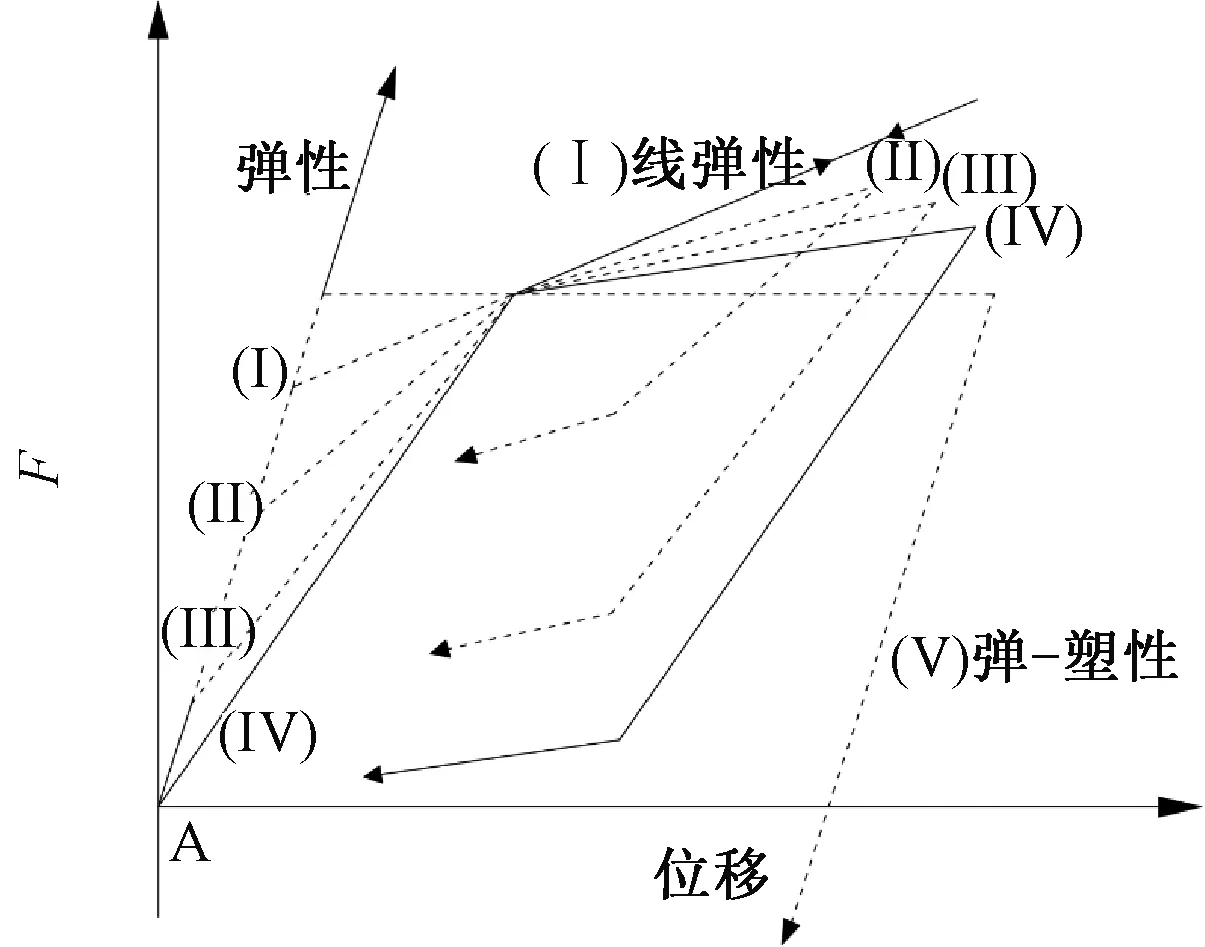
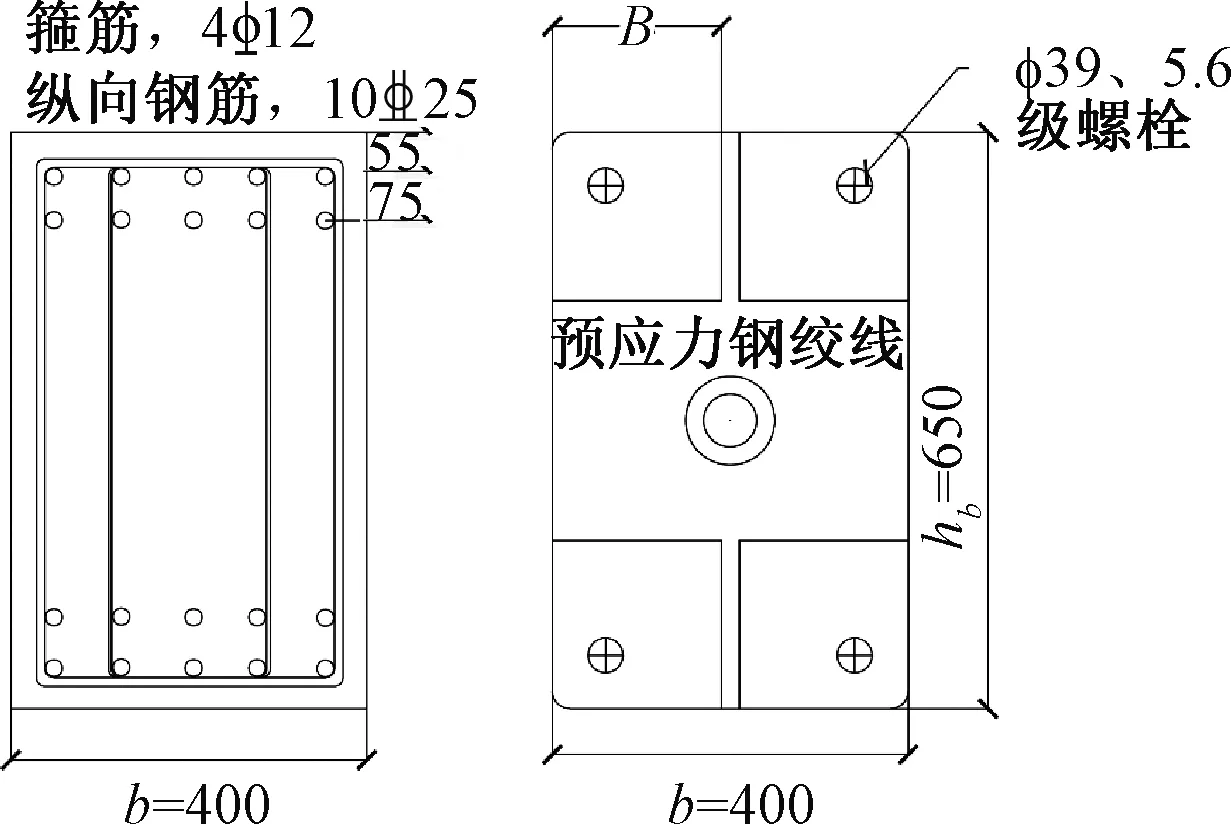
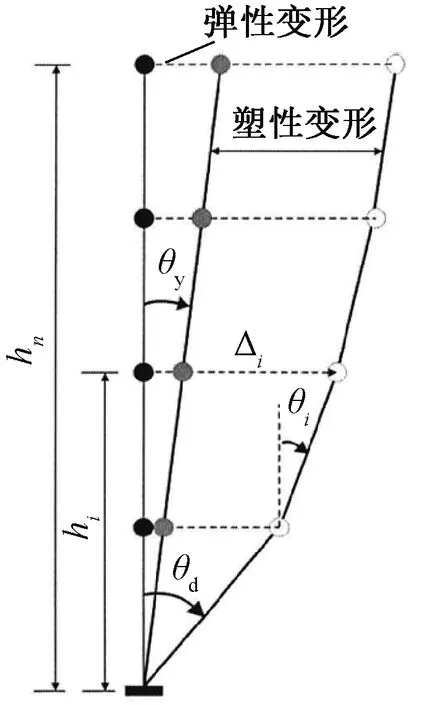
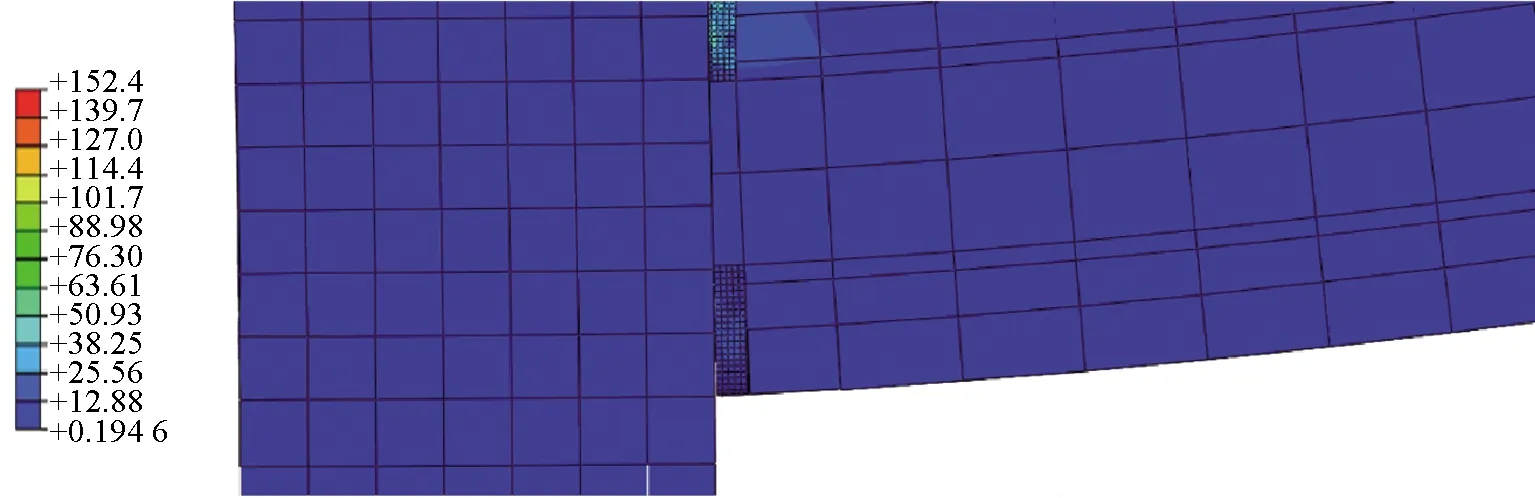
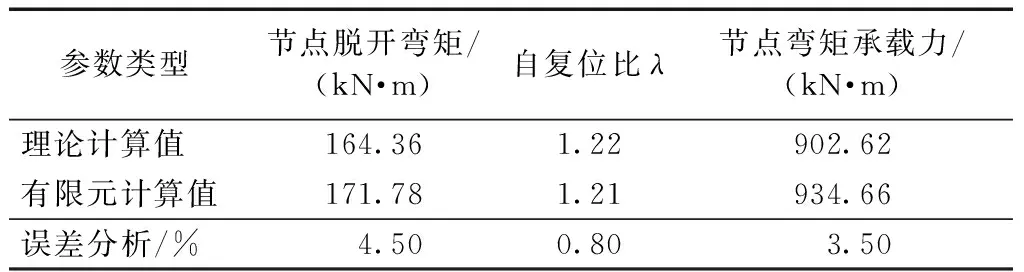
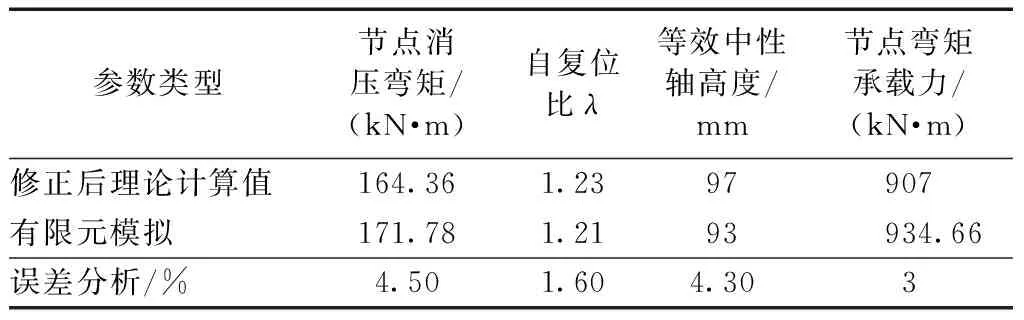
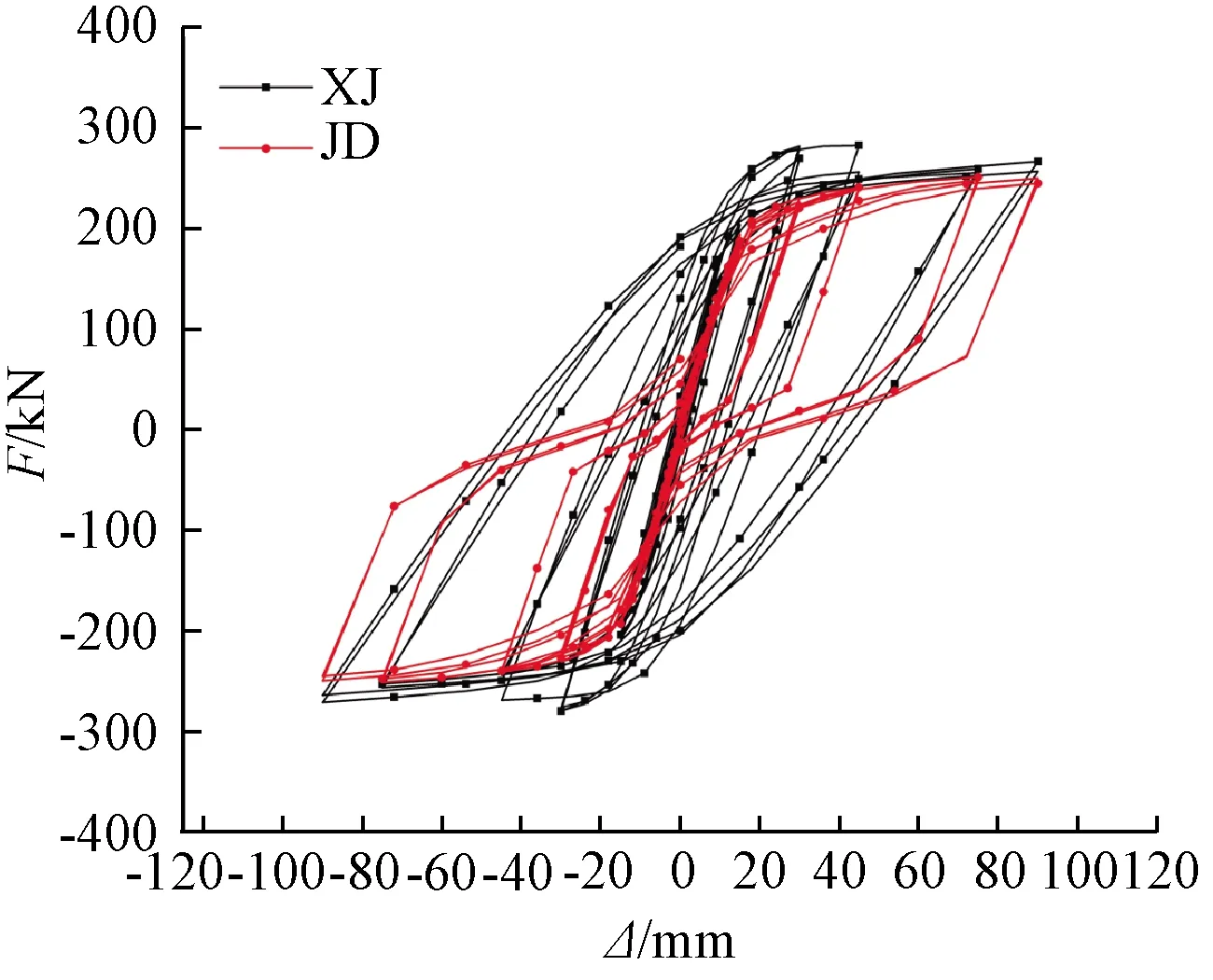
第一次卸载:由于系统之前开始向左运动,弹簧(对应Kp)继续伸长,代表预应力筋内力的增加。此时摩擦块已经滑动一定距离,摩擦力方向向右。但开始逐渐撤掉外力时,系统受力为外弯矩M、后张预应力张力作用产生的夹紧力矩Mpe、Kp产生的弯矩以及螺栓的屈服弯矩Mmy。由于M是逐渐减小的,保证了卸载的每一刻有M a—滞回曲线CG段; b—滞回曲线G点; c—滞回曲线GD段。图7 第一次节点闭合隔离体受力Fig.7 The force diagram of the isolator as the joints closed for the first time 第二次加载:与第一个循环不同的是,此时螺栓对应的弹簧(相应Km)是受压的,地面提供的等效摩擦力向左,即螺栓开始时受压屈服。当开始有外力M时,弹簧Kb伸长,此时对应曲线OA的消压阶段。当M=Mpe-Mmy时,对应图4滞回曲线A点,这时梁和柱即将分离,所以A点称为第二次循环的消压点。当M继续增大,地面的摩擦力Ff开始逐渐减小到零,如图8a所示,即对应曲线的AF段,螺栓所受的压应力逐渐减小,M继续增大时,Mm逐渐减小到0,对应图4中滞回曲线F点,螺栓的受力为零。随着M继续增大,摩擦力Mf开始反向,系统开始有向左运动的趋势,故摩擦力方向向右,如图8b所示,此阶段对应滞回曲线FB段,螺栓开始受拉。AB阶段,对摩擦块取隔离体分析,弹簧(对应Km)的受力从受压变为受拉,所以这阶段该弹簧会有少量的伸长,故弹簧(对应Kp)也会有等量的伸长。当M增大到一定值时,即Mm增大到Mmy,摩擦块开始滑动,对应图4滞回曲线BC段,螺栓开始屈服,此时系统的刚度只由预应力筋(对应Kp)来提供。如果M继续增加,达到E点对应的弯矩时,则预应力筋会开始屈服,无法实现完全自复位,所以在实际地震中要保证预应力筋不屈服。 a—滞回曲线AF段; b—滞回曲线FB段。图8 第二次节点张开时隔离体受力Fig.8 The force diagram of the isolator as the jointsopened for the second time 由上述分析可知,第二次加卸载循环后的节点打开和关闭力矩Mdec可由式(7)给出: Mdec=Mpe-Mmy (7) 根据Mole[4]的推导,螺栓和预应力筋的几何结构如下:螺栓的屈服应力、后张拉预应力筋的屈服应力和后张拉应力分别为σmy,σpy,σpe;螺栓和预应力筋的无黏结长度、内力臂、杨氏模量和面积分别为lm,lp,dm,dp,Em,Ep,Am,Ap;混凝土结构层高、开间宽度和转动刚度分别为H,L,Kb。 如图9所示,弯矩-转角关系不同斜率可以定义为式(8): 图9 自复位节点弯矩-转角关系Fig.9 Relations between the bending moment and rotation angle of self-resetting joint K1=Kb (8a) (8b) (8c) 式中:Km为螺栓的刚度。 为了简化一些参数,可以定义与后张预应力筋的后张应变和屈服应变以及螺栓的屈服应变相关的三个无量纲参数,它们与所用钢材的实际面积无关。当梁柱节点产生转角,则后张预应力筋和螺栓应变都会发生改变,可以分别计算后张预应力筋达到后张应变、屈服应变以及螺栓达到屈服应变所需的转角大小,对应的转角为式(9)。 (9) 则对应的弯矩如式(10): Mmy=Amσmydm=Kmθmy Mpe=Apσpedp=Kpθpe Mpy=Apσpydp=Kpθpy (10) 当Mdec=Mpe-Mmy时后张预应力只是保证连接的关闭,以抵抗压缩屈服中螺栓的阻力。往复加载下,当螺栓从受拉屈服回到初始状态时为一个初始应变;再从初始状态到受压屈服又是一个屈服应变,因此这里假设螺栓在一个滞回循环中达到2个屈服应变,并且这种假设在随后的所有循环中都成立。 根据节点打开后的弯矩等于旋转刚度乘连接件的转角,即式(11): ΔMj=(Km+Kp)Δθj (11) 当螺栓在拉力下屈服时,连接处的弯矩从Mdec增加到节点的屈服弯矩Myld,梁柱之间的转角使螺栓从受压屈服变为受拉屈服,如式(12): Myld-Mdec=2θmy(Km+Kp) (12) 根据螺栓和预应力筋的弯矩-转角关系,可得到螺栓的屈服弯矩Mmy和预应力筋的张拉弯矩Mpe的计算式如式(13): Mmy=Kmθmy (13a) Mpe=Kpθpe (13b) 式(12)可以改写为式(14): (14) 则由式(7)可得: (15) 则螺栓的截面面积就可以用式(16)表示: (16) 类似地,对于后张预应力筋对应式(17)、式(18): (17) (18) 从式(16)可以看出,当Am=0时,Mdec的值最大,可以得到式(19): (19) 从式(16)推导出螺栓杆截面最大面积的表达式,即节点能够实现自复位的螺栓杆截面最大面积Am,如式(20): (20) 为了反映不同滞回曲线的形状,采用参数η来定义,η定义为理论消压力矩最大值Mdec(max)和消压力矩Mdec的差值与理论消压力矩最大值Mdec(max)的比值,如式(21)。如图10所示,当η取最小值0时,代表Mdec取得最大值Mdec(max),此时节点中无螺栓,对应曲线Ⅰ。当η取最大值1时,Mdec等于零,代表Mpe=Mmy,预应力筋在螺栓屈服时开始提供恢复力,对应曲线Ⅳ。 图10 不同旗帜滞回曲线形状Fig.10 Different flags hysteresis curve shape (21) 因此,Am和Ap可以用式(22)表示: (22a) (22b) (23a) (23b) 在此基础上结合式(10),对当η=1时的节点夹紧力矩和螺栓屈服时的弯矩进行了推导。当η=1对应曲线Ⅳ,正好经过原点。根据式(10)可以得到式(24): (24a) (24b) 将Mpe与Mmy相比得到式(25): (25) 证明当Mpe和Mmy相等时,自复位节点的滞回曲线经过原点。滞回曲线是在螺栓开始压缩屈服时循环的,证明当预应力筋提供的初始夹紧弯矩Mpe刚好能够克服螺栓压屈引起的阻碍弯矩Mmy时,能够实现完全自复位。 为了更好地对比研究,装配式干连接自复位节点的尺寸与文献[5]中传统自复位节点尺寸一致。其中梁长度7.5 m,截面尺寸650 mm×400 mm,层高3.8 m,柱截面尺寸700 mm×700 mm,混凝土强度等级为C50。以文献[6]中的设计弯矩值为基本参数,对自复位装配式干连接节点进行设计。 干连接自复位节点的设计本质上是基于混凝土双筋截面设计思路,由于有预应力的存在,导致截面的配筋结果不唯一,需提前规定好预应力筋和螺栓数量上相对关系,采用无黏结预应力筋和轴向荷载提供的自复位弯矩贡献和螺栓提供的耗能弯矩的比值作为主要设计参数,即自复位比λ,如式(26)。节点的自复位比是衡量节点自复位性能的重要指标,代表着节点恢复性能与耗能性能之间的相对关系。 (26) 式中:Mpt为设计位移时预应力筋提供的弯矩;MN为设计位移时轴向荷载提供的弯矩;Ms为设计位移时螺栓提供的弯矩。 首先将其等效为混凝土双筋截面进行设计,如图11所示,弯矩承载力可以通过式(27)估算: 图11 梁截面 mmFig.11 Cross section of the beam (27) 对于弯矩设计值,根据文献[6]中提供的基于位移设计方法的弯矩设计值为611 kN·m。由式(27)可得钢筋总面积As=5 153 mm2。 根据文献[5]附录B4.3.2的建议:考虑螺栓应变硬化的余量,将自复位比限定在1.15以内。然而在本设计示例中,选择了更大的自复位比1.25,这是为了提供更大的保护,防止需要重新确定基于位移设计期间的设计阻尼。推导得到的弯矩参与系数αOTM,βOTM如式(28)~(30)。 (28) (29) (30) 因此可以得到柱内预埋耦合器截面面积为2 267 mm2,故选用直径为39 mm的螺栓。如图12所示,选取佩克螺栓对应的型号为COPRA39H的柱内预埋耦合器,对应截面面积为2 388 mm2。 图12 内螺纹耦合器示意及相关参数Fig.12 The schematic diagram of internal thread coupler and related parameters 根据相关数据,需选用8.8级高强螺栓,但由于自复位性节点有后张预应力作用,故可以选用5.6级的螺栓,屈服强度为300 MPa。由于选用COPRA39H的耦合器,螺栓的面积大于设计钢筋的面积,为了保持自复位比λ=1.25不变,需要对弯矩设计值进行调整。 对应需要选用佩克螺栓对应BECO39H型号的梁靴,根据佩克螺栓要求,梁靴对于梁高和梁宽的最小尺寸要求为390 mm,故设计梁截面尺寸b×h=400 mm×650 mm符合要求。根据图13梁靴的设计参数可知,干连接自复位节点中螺栓在梁截面的力臂d-d′=530 mm。 图13 梁靴示意及参数Fig.13 The schematic diagram and parameters of beam shoe 由于螺栓总面积比设计值大,为了保证自复位比,需要重新调整弯矩设计值,调整梁截面设计弯矩为410.76 kN·m。根据自复位λ=1.25,后张预应力筋的弯矩应满足设计弯矩56%的要求,如式(31): (31) 后张弯矩由式(32)给出: φMpt=φTptjd (32) 式中:Tpt为设计位移时后张预应力筋的总内力;jd为预应力筋在梁截面的内力臂。 预应力筋在梁截面的内力臂可以通过估计质心相对于混凝土受压合力点距离来确定。如果无量纲中性轴深度γ=0.2,且混凝土等效应力系数α=1,β=0.8。如图14所示,则内力臂jd可用式(33)计算: 图14 梁截面变形Fig.14 Deformation diagram of beam section jd=0.5hb(1-βγ)=0.42hb (33) 则由式(32)得到设计位移所需的后张预应力筋的拉力为1 790 kN。根据设计要求:预应力筋达到设计位移时,内力不超过其屈服强度的90%,预应力筋数量npt通过式(34)确定,最终得到npt=10。 (34) 估算出后张预应力筋总数后,接下来确定预应力筋的初始预拉力。每个预应力钢筋束的初始应力可以通过设计位移时的预应力筋内力与预应力筋因截面开口引起的增量之差来确定,则预应力筋的总应变由式(35)确定: (35) 式中:n为沿无黏结预应力筋间隙开口总数(本例中n=1);Δpt为由于间隙开口导致的预应力筋伸长量;l为无黏结预应力筋长度;θ为截面的转角。 通过计算可初步确定基于干连接自复位梁的设计由10根截面面积143.3 mm2的钢绞线和4根直径39 mm的螺栓组成。 由于自复位连接体系中无黏结段钢筋与混凝土应变之间不协调,因此传统的平截面法则不再适用。2001年Pampanin等提出了类比现浇梁法,提供了除整体受力外的变形协调条件,得到混凝土应变与中性轴间的关系,再通过迭代法最终得到截面受力状态[7]。混凝土应变可以表示为式(36): (36) 式中:c为中性轴距梁截面受压边缘距离(等效中性轴与梁截面受压边缘的距离);θimp为梁柱刚性转动夹角;Lcant为界面到梁反弯点的距离(即悬臂梁的长度);Lp为等效塑性铰长度;φy为混凝土屈服曲率。 类比现浇梁法的理论基础为:两种类型梁,一种为自复位连接形式的预制梁,另一种为现浇梁,两者有相同的几何尺寸和配筋,弹性变形相同,当施加同样的总位移时,则塑性变形也相同,即预制梁梁柱连接的塑性贡献与现浇梁梁端的塑性铰贡献相同。通过类比现浇梁法提供的整体构件变形协调方程,从而可以确定干连接自复位节点的弯矩承载力。具体方法为:先设定一个转角θimp,然后假定一个等效中性轴高度c,利用构件整体变形协调,由式(36)求得εc。然后计算混凝土压力,接着通过截面静力平衡,反求满足静力平衡的等效中性轴高度c′,比较c与c′的差值是否在限值内,否则返回第一步迭代,直到满足|c′-c|<δ时,求出此时的弯矩,即可以得到转角θimp对应的弯矩M。 梁柱连接处的设计转角实际上是由弹性变形和塑性变形组成的,如图15所示。 图15 结构弹性变形与塑性变形Fig.15 Elastic and plastic deformation of the structure 基于位移方法的设计思想,当结构层数不超过4层,即n≤4时,结构振型可以采用线性振型,如式(37): (37) 式中:Hi为结构第i层的高度;Hn为n层结构的总高度。 对于超过4层(n>4)时,结构振型采用非线性振型,如式(38)。 (38) 每个楼层的位移由式(39)给出: (39) 式中:δc为关键楼层的振型因子;Δi为关键楼层的位移。 一般情况下,关键楼层的位移在框架结构的首层,位移由设计层间位移角θd乘以首层高度Hi=1,如式(40)。 Δc=θdHi=1 (40) 本文选取两榀五跨框架作为设计实例进行分析,该框架横向跨度7.5 m,纵向跨度12 m,层高3.8 m。框架横向选择θd=2%的层间位移角限值,设计位移角θd可以表示为弹性位移角θy和塑性位移角θp之和,且不得超过最大允许层间位移角限值θc,见式(41)。表1给出了每一层的θi、θp、θ值。 表1 各个楼层梁柱转角Table 1 Beam-column to Corners on each floor θd=θy+θp≤θc (41) 式中:θy为具有无黏结后张预应力筋的框架屈服位移。 因为确定截面等效中性轴高度需通过迭代计算,因此本文编写MATLAB程序进行计算,最后一步迭代的等效中性轴高度c=101.11 m,γ=c/hb=0.16。此时等效中性轴高度误差为0.01,则对应的弯矩承载力可通过式(4)计算,所得总弯矩承载力满足要求,并且节点的自复位比λ=1.22,符合设计要求。 为了验证该设计方法的准确性,对节点性能进行有限元分析,建立了如图16所示的有限元模型,通过计算模拟出截面等效中性轴高度及各个组件的内力来计算节点的性能。为了方便加载及后张无黏结预应力筋的设置,在梁的一端设置加载端头,构件的尺寸与设计梁柱节点的尺寸保持一致。 图16 装配式干连接自复位节点有限元模型Fig.16 The finite element model of self-resetting joints of prefabricated dry-connection 节点消压弯矩等于梁与柱刚分离时的端部反力与梁跨度之积。梁柱脱开时的有限元模型如图17、图18所示。节点张开时,梁截面底部的正应力应为零。由图19可知,A点对应的反力为45.54 kN。所以此节点的消压弯矩为:Mdec=FL=45.54 kN·3.75 m=171.78 kN·m。 图17 节点张开时梁柱应力云图 MPaFig.17 Stress nephogram of beam-column as the joints opened 图18 节点张开时梁截面正应力 MPaFig.18 The normal stress diagram of the beam section when the joints were opened 图19 节点试件的荷载-位移曲线Fig.19 Load-displacement curves of joints 在ABAQUS中可以查询到设计位移时各个部件的应力状态,如图20所示,进而求得节点的自复位比,该节点的设计状态为θ=1.58%。 a—梁截面;b—螺栓;c—预应力筋。图20 设计位移时各个部件应力云图 MPaFig.20 Stress nephogram of each component during design displacement 由图20b的螺栓应力云图可以看到,螺栓应力主要集中在未与套筒连接部分,因此震后只需将损坏的螺栓转出,重新安装上新的螺栓,即可恢复结构的正常使用。该连接具备损坏位置可控,震后可快速修复的特性。 表2汇总了节点力学性能的有限元模拟结果与理论计算结果。可见:理论计算值与有限元计算值结果基本吻合,误差都在5%以内,同时也验证了建模方式的合理性和准确性。 表2 节点力学性能的理论计算与有限元计算值Table 2 Theoretical and finite element calculation values of the mechanical properties of joints 新型节点的梁是由梁端梁靴和混凝土并联再与剩余不含梁靴的混凝土梁串联组成,其各部分刚度由式(42)计算: (42a) (42b) (42c) 式中:Ks、Kc分别为梁中含梁靴段的轴向刚度和不含梁靴段的刚度;As为梁端梁靴的面积;Asc为梁靴部分含混凝土的面积;Ac为不含梁靴部分混凝土的面积;ls为梁靴的等效长度(需考虑锚固钢筋的影响);lc不含梁靴的混凝土梁长度。其中ls的计算方法根据图21所示,按式(43)计算。 a—梁正立面; b—梁侧立面; c—梁靴尺寸。图21 梁尺寸示意Fig.21 Beam sizes (43) 采用修改后得到的梁抗压刚度为52 MPa,代入程序得到计算结果如表3所示。 表3 节点力学性能的修正后理论计算与有限元计算值Table 3 Modified theoretical and finite element calculation values of the mechanical properties of joints 修正后的理论值与有限元值的误差为4.3%,更加接近有限元值。可见修改后的梁抗压强度更接近实际中预埋梁靴后预制梁抗压强度。 为了更好地分析自复位装配式干连接节点抗震性能,根据上述建模,对现浇节点和干连接自复位节点进行滞回分析,分别提取了节点模型的滞回曲线,如图22所示。可以看出,现浇节点的滞回曲线饱满,具备较好的耗能能力,但当后期卸载后,节点的位移不为0,此时节点存在残余变形,不具备自复位性能;干连接自复位节点也具备良好的耗能性能,且加载卸载后,节点基本没有残余变形,节点具备良好的自复位性能。 图22 节点滞回曲线Fig.22 Hysteretic curves of joints 由图22可以看出:在几次滞回循环后,干连接自复位节点的滞回曲线开始出现了残余变形,与理论分析的滞回曲线存在差异,因为实际加载时混凝土梁也会受力,并产生塑性变形,而理论分析只考虑了螺栓和预应力筋的相对关系,所以到加载后期,混凝土梁端产生塑性损伤,导致节点在加载后期存在微小残余变形。 提出一种新型干连接自复位节点形式,利用装配式和自复位相结合的设计方法,对螺栓连接进行了节点设计,并通过编写迭代法程序计算其承载力。通过有限元软件ABAQUS对装配式干连接自复位节点进行单调加载下的数值模拟,验证了该设计方法的准确性,得到以下结论: 1)传统自复位节点与现浇混凝土双筋截面设计不同之处在于:由于有预应力的存在,导致截面的配筋结果不唯一,需要提前规定好预应力筋和螺栓数量上的相对关系,采用无黏结预应力筋和轴向荷载提供的自复位弯矩贡献和螺栓提供的耗能弯矩的比值作为主要设计参数,即自复位比λ。 2)通过对新型节点的滞回曲线的对比分析,解释了第一次张拉和第二次张拉时螺栓初始状态的不同。详细解释了节点张开、闭合过程中,混凝土、螺栓、预应力筋的受力变化,以及相应的等效质量模型中各个弹簧和摩擦块在张拉过程中相应的受力变化。 3) 当系统的消压力矩完全等于耗能螺栓的初始屈服弯矩时,也就是在卸载过程中预应力筋刚好能够使耗能螺栓屈服时,干连接自复位节点的滞回曲线经过原点。 4)采用该设计方法计算出的弯矩承载力误差不超过5%,造成有限元模拟数值较高的主要原因是理论计算中没有考虑截面梁靴对节点抗压承载力提升的影响。但梁靴对截面弯矩承载力的影响在误差允许范围内,故在实际工程实践中仍然可以采用该方法进行计算。
1.3 影响自复位滞回曲线形状因素分析

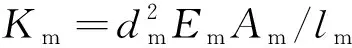
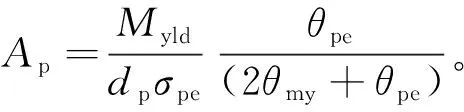
2 干连接自复位梁柱节点设计
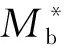



3 节点承载力的理论计算


4 有限元验证

4.1 节点消压弯矩计算


4.2 节点自复位比和弯矩承载力计算


4.3 基于有限元结果对理论计算中性轴进行修正
4.4 节点滞回特性分析
5 结束语

