冷弯型钢锁铆连接抗剪性能非线性有限元简化分析方法研究*

谢志强 石磊磊 张爱林 周大兴 张向东 殷炳帅 王 凯

(1.北京建筑大学土木与交通工程学院, 北京 100044; 2.中铁建设集团有限公司， 北京 100040)

0 引 言

近年来，国家大力发展绿色装配式钢结构建筑，冷弯薄壁型钢结构因其具有绿色环保、轻质高强、抗震性能好、工业化和装配化程度高等优势[1]，在低、多层建筑中得到了广泛的应用。

锁铆连接是机械工程领域中常用的薄板连接技术，具有承载力高、刚度大、抗疲劳性能好等特点，特别是其连接效率及自动化程度极高[2]，在装配式冷弯薄壁型钢结构中具有较好的应用前景。锁铆接头成形机理如图1所示[3]。对于冷弯薄壁型钢结构或构件的有限元分析，锁铆连接力学性能的有效模拟是影响其数值计算精度与正确性的关键。此外，每栋建筑的结构构件上有成千上万个连接点，锁铆连接不能实现精细化建模[4]；并且，锁铆接头的有效区域尺寸小、构造复杂，实体精细化建模极其复杂、分析时非线性极强，导致计算效率低、耗时长。因此，为了实现冷弯型钢锁铆连接的抗剪性能有效模拟和计算效率提升，研究其非线性有限元简化分析模型和方法非常有必要。

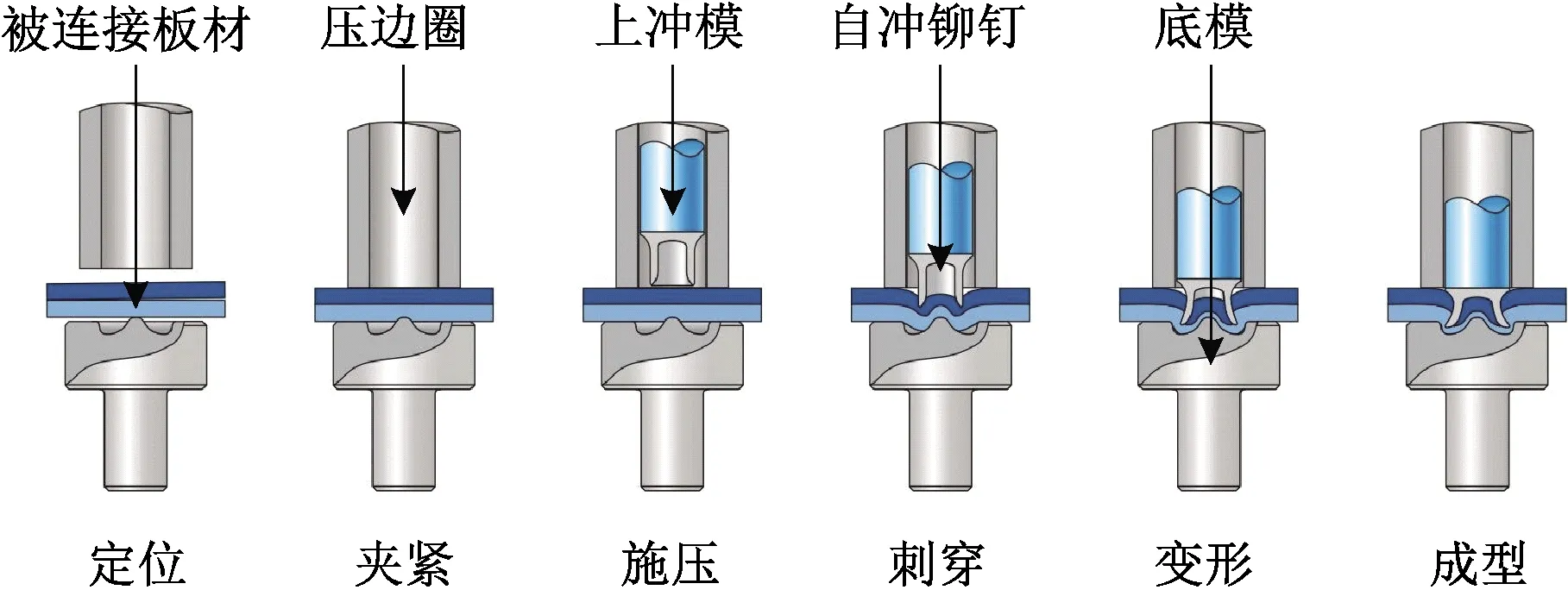
图1 锁铆接头成形机理示意[3]Fig.1 The schematic diagram of the forming mechanism for SPR joint

文献[5-6]采用实体精细化有限元模型对铝材锁铆接头的成形过程和连接的受剪性能进行了数值模拟，结果表明精细化模型能较精确模拟出锁铆连接的荷载-位移曲线。Hoang等将锁铆连接等效为有限元接头-连接器模型，并采用非线性有限元分析方法模拟出了完整的力-位移曲线[7]。Porcaro等提出了锁铆接头从二维到三维有限元模型信息转换的算法，利用三维模型模拟出了其在不同破坏模式下的力-位移曲线，并针对不同的破坏模式提出了相应的有限元分析方法[8]。Huang等对铝板与钢板自冲铆接的成型机理进行了数值模拟，获得了铆接成形过程与应力应变分布和荷载-位移曲线的关系[9]。Han等提出了锁铆连接成型过程的二维轴对称数值模型[10]。徐纪栓提出了基于锁铆接头失效精细化模型标定的简化分析方法，对比了实体单元模型和SPR约束单元简化模型对锁铆接头失效模式的模拟效果[11]。钟毅等综合考虑材料接触形式和截面形状建立了有限元简化模型，结果表明这种模型能够模拟出锁铆连接拉剪过程中的破坏模式和拉剪强度[12]。周璐瑶等分别采用梁单元、实体单元和约束单元对锁铆连接进行简化模拟，并对这三种单元进行十字拉伸和搭接剪切模拟的对比分析[13]。

综上，国内外的学者采用有限元精细化模型对锁铆连接的成型机理、强度预测、疲劳性能等研究较为成熟，而对其受剪性能的简化模型和非线性有限元分析方法的研究还不足。本研究从材料的宏观和微观本构关系角度出发，采用等效面域偶合、约束单元、连接单元三大类8种简化方法建立锁铆连接的受剪有限元模型；并以试验结果为参考，对比分析8种简化模型的建模特点、计算效率、计算精度和破坏特征，明确各种简化模型的适用范围；在此基础上，开展不同板厚比下锁铆连接受剪性能的参数化数值模拟，并提出冷弯薄壁型钢结构中锁铆连接非线性有限元简化分析的方法和建议。

1 锁铆连接抗剪性能试验

1.1 试件设计

考虑板厚比和铆钉长度因素，设计制作了12组冷弯型钢锁铆连接抗剪试件，每组3个试件，试验结果取其平均值。试件采用0.8，1.0，1.2，1.5，2.0 mm厚的镀锌钢板组合，试件的钢板长度为220 mm，宽度为80 mm，铆钉端距为20 mm。锁铆连接抗剪试件示意如图2所示。

图2 锁铆连接抗剪试件 mmFig.2 The SPR connection specimen for shear test

锁铆连接采用的铆钉尺寸定义如图3所示，其中，钉头直径D为7.6 mm，钉管直径d为5.3 mm。此外，为了保证铆钉能刺穿上层板材并刺入下层板材而形成可靠的紧固机构，不同厚度组合的板材需对应不同长度的铆钉。基于前期大量锁铆接头的质量评估测试，确定不同厚度组合钢板所需的铆钉长度和试件编号如表1所示。试件编号的规定如下：例如“S0.8+1.0”表示上、下层钢板的厚度分别为0.8,1.0 mm。

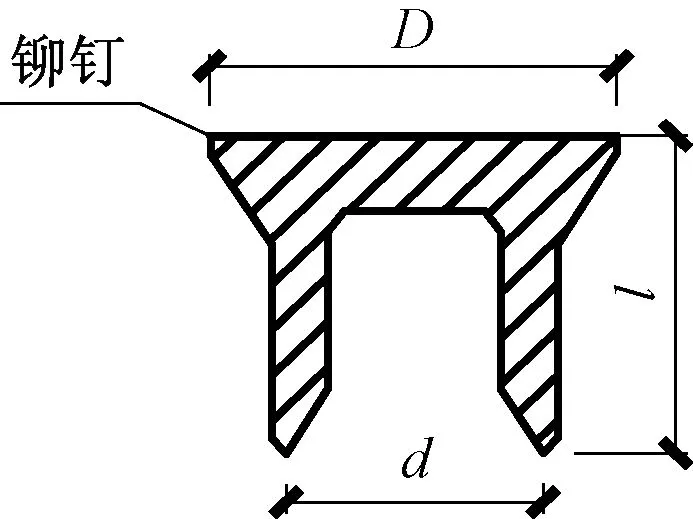
图3 铆钉示意Fig.3 The schematic diagram of rivet

表1 试件编号和铆钉长度Table 1 Specimen number and rivet length

1.2 加载设备和加载制度

冷弯型钢锁铆连接抗剪性能试验在拉伸实验机(图4)上进行，采用位移控制的单调加载，加载速度为3 mm/min。试验时采集荷载-相对位移曲线数据并观察破坏过程，接头相对位移由自动引伸计测量，测量标距为100 mm。

图4 加载设备Fig.4 Loading equipment

1.3 试验结果

1.3.1 破坏模式

表2给出了12组冷弯型钢锁铆连接试件的抗剪承载力、最大相对位移和破坏模式。其中，破坏模式Ⅰ为铆钉腿拔出下层钢板；破坏模式Ⅱ为铆钉头剪脱上层钢板。

表2 试验数据Table 2 Test results of experiment

由表2可知，板厚比t2/t1(其中，t1表示上层钢板，t2表示下层钢板)是影响冷弯型钢锁铆连接在剪切作用下的破坏模式的主要因素。锁铆连接在剪切作用下的主要破坏模式可以归纳为如下两种：当板厚比t2/t1<1.5时，试件发生破坏模式I (图5a)；当板厚比t2/t1≥1.5时，试件发生破坏模式II (图5b)。

a—铆钉腿拔出下层钢板；b—铆钉头剪脱上层钢板。图5 锁铆连接的破坏模式Fig.5 Failure modes of SPR connection

1.3.2 破坏过程

图6给出了破坏模式I下试件的荷载-位移曲线。由图6及试验现象可知，可将试件在破坏模式I下的破坏过程简化为三个阶段：1)弹性阶段：锁铆接头的上、下层钢板及紧固机构处于弹性阶段，荷载-位移曲线呈线性增长的关系；2)塑性阶段：接头的上层钢板端部开始翘曲变形，紧固机构发生塑性变形，荷载-位移曲线趋于平缓；3)破坏阶段：上层钢板孔壁发生塑性变形，铆钉倾斜并逐渐被拔出，接头失效，荷载-位移曲线趋于急剧下降阶段。

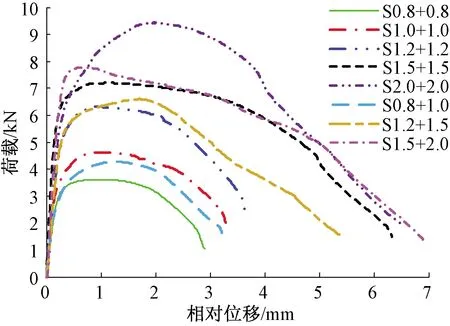
图6 破坏模式I的荷载-位移曲线Fig.6 Load-displacement curves of failure mode I

图7给出了破坏模式II下试件的荷载-位移曲线。由图7及试验现象可知：破坏模式II下试件的破坏过程可以简化成4个阶段：1)弹性阶段：与破坏模式I类似；2)弹塑性阶段：上层钢板孔壁局部挤压变形，钢板强度进入强化阶段，紧固机构仍处于弹性，荷载-位移曲线呈非线性增长的关系；3)塑性阶段：铆钉孔迅速扩张，铆钉与钢板间产生相对滑移，钢板强度进入下降段，紧固机构进入弹塑性，荷载-位移曲线趋于平缓；4)破坏阶段：孔壁发生挤压撕裂，铆钉头部完全脱离上层板材，紧固机构处于塑性阶段，荷载-位移曲线趋于急剧下降阶段。

图7 破坏模式II的荷载-位移曲线Fig.7 Load-displacement curves of failure mode II

2 锁铆连接有限元简化分析方法

2.1 有限简化分析方法

锁铆连接的有限分析采用ABAQUS软件平台开展，连接板均采用薄壳单元S4R简化建模；按照剪力的传递方式不同，锁铆接头的有限元简化建模方法可分为以下三类：1)通过接头区域的等效面域偶合传递剪力；2)通过接头区域节点的约束单元传递剪力；3)通过接头区域的连接单元传递剪力。

综合受剪锁铆试件中单元的简化情况及三类锁铆接头的剪力传递方式，可以组合成8种不同的有限元简化分析模型，表3给出了三大类8种有限元简化模型的计算简图及建模方法。

表3 锁铆连接有限元分析简化方法Table 3 Simplified method of finite element analysis for SPR connection

2.2 薄壁钢板的材料本构关系

2.2.1 材料性能试验

根据GB/T 228.1—2010《金属材料 拉伸试验第1部分:室温拉伸试验方法》[14]，连接板取3个样品进行拉伸试验，材料特性取3个试样的平均值。图8给出了3个1.5 mm厚钢板的应力-应变曲线。

图8 1.5 mm钢板应力-应变曲线Fig.8 Stress-strain curves of 1.5 mm thickness steel sheet

2.2.2 本构关系

通过材料性能试验获得的钢板应力-应变关系通常是材料的名义应力和名义应变，然而，在ABAQUS分析中，由于计算时需要考虑材料非线性和几何大变形。因此，需将材料的名义应力和名义应变转换成真实应力与真实应变[15]。转换式如下：

σture=σnom(1+εnom)

(1a)

εture=ln(1+εnom)-σture/E

(1b)

由式(1)将钢板的名义应力与名义应变关系转化成真实应力与真实塑性应变的本构关系如图9所示。

图9 真实应力-真实塑性应变的本构关系Fig.9 The constitutive relation between true stress and true plastic strain

2.3 锁铆连接的受剪本构模型

锁铆连接采用连接器单元、弹簧单元等连接单元简化模拟时，需对两节点间的连接单元输入宏观的力-变形本构关系。连接单元的本构模型均基于第1节锁铆连接抗剪性能试验结果的荷载-位移曲线简化而来，其简化原理如图10所示。由图10可知，连接单元的本构模型可以简化成五个阶段：1)弹性阶段(OA)：模拟连接通过紧固机构传递力的弹性行为；2)弹塑性阶段(AB)：模拟上层板材翘曲变形、铆钉倾斜引起的弹塑性行为；3)塑性阶段(BC)：模拟铆钉与钢板间的滑移行为；4)破坏阶段(CD)：模拟铆钉剥离板材而导致连接完全失效的行为；5)破坏阶段(DE)：为了防止个别铆钉失效引起整体试件计算不收敛，将曲线DE段处理成荷载大小可忽略的水平段。基于试验结果简化而来的锁铆连接剪切行为本构关系如图11所示。

图10 连接单元本构模型简化原理Fig.10 Simplification principle of constitutive model for link element

图11 锁铆连接受剪本构模型Fig.11 The shear constitutive model of SPR connection along the rivet axis

2.4 边界条件

简化分析模型忽略接头成形时产生的预紧力，铆钉与钢板的紧固力、钢板与钢板间的摩擦力简化成钢板间受力区域的剪切作用。简化分析模型的边界条件为：左端所有节点释放绕Z轴转动的自由度Rz，右端所有节点释放绕Z轴转动的自由度Rz及X方向(加载方向)平动自由度Ux，其余自由度均约束；荷载施加方式为：首先将试件右端的节点耦合到一个参考点并释放X方向的约束，然后在该参考点上施加X方向的位移荷载。

3 有限元简化分析结果与验证

3.1 有限元简化分析结果

针对表3三大类8种有限元简化模型，均采用位移加载的静态求解，最大加载位移为6 mm，并考虑材料的非线性、几何大变形、部分有限元模型的非线性接触和von Mises屈服准则。8种有限元模型求解的Mises应力云图与破坏形式如图12所示，其剪切荷载-变形曲线如图13所示。

3.2 结果验证

基于有限元简化分析结果与试验结果，表4和表5将8种简化分析模型与试验构件进行对比。

由表4和表5分析可知：

表4 有限元简化分析模型对比Table 4 Comparison of simplified finite element analysis models

表5 有限元分析与试验结果对比Table 5 Comparisons of finite element analysis results and test results

1)采用等效面域耦合简化方法的有限元模型能较精确地模拟锁铆连接的破坏特征，其在弹性阶段的剪切荷载-变形曲线与试验结果相似程度较高，但其在塑性阶段和破坏阶段的计算难以收敛，且该模型的网格较复杂，计算效率低；此外，考虑板间硬接触的模型(编号1-2)的荷载-变形曲线有较明显的塑性段。综上分析，等效面域耦合的有限元★的数量表示复杂程度；T为计算时间。

a—模型1-1；b—模型1-2;c—模型1-3；d—模型2-1;e—模型2-2；f—模型2-3;j—模型3-1；h—模型3-2;i—试件S1.5+1.5的破坏模式。图12 有限元简化分析的应力云与破坏模式Fig.12 Stress cloud diagrams and failure modes of simplified finite element analysis

a—第一类简化模型；b—第二类简化模型；c—第三类简化模型。图13 有限元分析的剪切荷载-变形曲线Fig.13 Relations between shear load-deformation in finite element analysis

Ke/Ktest为有限元计算与试验的抗剪刚度之比；Pu/Ptest为有限元计算与试验的抗剪承载力之比；εu/εtest为有限元计算与试验的极限变形量之比；εm为有限元计算的最大变形量。

简化分析方法仅适用于研究锁铆接头局部的受力性能和破坏模式，且考虑板间接触可提高塑性变形的计算量，有效解决由于单元变形过大导致计算不收敛的问题。

2)采用约束单元简化方法的有限元模型对锁铆连接破坏特征的模拟效果较差，且其三种模型的剪切荷载-变形曲线的趋势相差较大。MPC-Pin单元模型在弹性、弹塑性和塑性阶段的剪切荷载-变形曲线与试验结果相似程度较高，其抗剪刚度和抗剪承载力的计算精度较高，且其模型和网格复杂程度低，计算时间较短，但其在破坏阶段的剪切荷载-变形曲线与试验结果相差较大，且其塑性变形的计算精度较低；Fastener单元模型在弹性和塑性阶段的剪切荷载-变形曲线与试验结果相似程度较高，其抗剪承载力和塑性变形的计算精度较高，且其模型和网格复杂程度低，计算时间较短，但其在弹塑性阶段和破坏阶段的剪切荷载-变形曲线与试验结果相差较大，且其抗剪刚度计算精度较低。综上分析，约束单元Pin与紧固件单元Fastener适用于模拟未达到破坏阶段的锁铆连接的力学性能，而约束单元beam则不宜用于锁铆连接的非线性有限元简化分析。

3)采用连接器单元Cartesian Connector与弹簧单元Spring2简化方法的有限元模型在弹性、弹塑性、塑性和破坏阶段的荷载-变形曲线与试验结果相似程度较高，其抗剪承载力和塑性变形的计算精度较高，且其模型和网格复杂程度低，计算时间短，但其抗剪刚度计算精度较低且破坏特征与试验结果相差较大。综上分析，连接器单元Cartesian Connector与弹簧单元Spring2适用于研究锁铆连接构件的整体受力性能，且两者相比，连接器单元Cartesian Connector的计算效率与精度更高。

Xie等的试验结果[16]表明，龙骨框架中冷弯型钢构件间的锁铆连接均未出现破坏现象，而龙骨框架与面板间的锁铆连接破坏严重。因此，对于冷弯薄壁型钢结构中连接的非线性有限元简化分析，龙骨框架中冷弯型钢构件间的锁铆连接可采用约束单元Pin或紧固件单元Fastener进行简化模拟，龙骨框架与钢面板间的锁铆连接可采用连接器单元Cartesian Connector或弹簧单元Spring2进行简化模拟。

4 不同板厚比下的锁铆连接有限元参数分析

冷弯薄壁型钢结构中的锁铆连接可分为龙骨框架中构件间的等厚钢板连接，以及龙骨框架与钢面板间的不等厚钢板连接，且这些连接主要以承受剪力为主。因此，有必要对不同板厚比的冷弯型钢锁铆连接的抗剪性能进行有限元参数分析，为冷弯薄壁型钢结构的非线性有限元分析提供建议和参考。

4.1 简化分析方法选取

由第3节中锁铆连接多种简化建模方法的对比研究可知，笛卡尔连接单元Cartesian Connector模拟锁铆连接时，其力学行为可以模拟锁铆连接的剪切性能且不用考虑收敛问题。笛卡尔连接单元可模拟两点间3个平动与转动自由度的相对关系，其原理如图14所示。

a—平动连接;b—转动连接。表示坐标轴，i=1,2,3; a、b分别为坐标系中的点。图14 笛卡尔连接单元的平动与转动关系Fig.14 Translational and rotational relations of the Cartesian connector

4.2 有限元分析与结果

以板厚比t2/t1为参数，建立12组不同板厚比的冷弯型钢锁铆连接简化模型，并进行非线性有限元分析，有限元分析的剪切荷载-变形曲线如图15、16所示。

图15 t2/t1<1.5的剪切荷载-位移曲线Fig.15 Relations between shear load and displacement in the case of t2/t1<1.5

图16 t2/t1≥1.5的剪切荷载-变形曲线Fig.16 Relations between shear load and displacement in the case of t2/t1≥1.5

由不同板厚比的锁铆连接抗剪性能的试验结果和有限元简化模型分析结果可知，笛卡尔连接单元可精确模拟出不同板厚比锁铆连接各阶段的荷载-变形曲线趋势和抗剪性能。

当t2/t1<1.5时，锁铆连接发生破坏模式I，试验试件和简化模型的抗剪承载力随着钢板总厚度的增加基本成线性增加，说明其抗剪承载力由锁铆接头区域内紧固机构的受剪性能决定。在剪切作用下，钉头处的弯矩使上层钢板的板端发生翘曲变形，下层钢板中的紧固机构发生剪切破坏；当紧固机构的受剪能力小于上层钢板孔壁的承压能力时，紧固机构失效。

当t2/t1≥1.5时锁铆连接发生破坏模式II，试验试件和简化模型的抗剪承载力随上层钢板厚度的增加而增加，说明其抗剪承载力由上层较薄钢板孔壁与铆钉头间的承压能力决定。在剪切作用下，下层钢板中的紧固机构处于塑性，当上层钢板孔壁的承压能力小于紧固机构的受剪能力时，上层钢板的铆钉孔发生挤压撕裂破坏，铆钉头完全剪脱上层钢板。

综上所述，板厚比是影响锁铆连接受剪性能和破坏模式的关键因素，当t2/t1<1.5时，其抗剪承载力由锁铆接头区域紧固机构的受剪性能决定，当t2/t1≥1.5时，其抗剪承载力由上层较薄钢板孔壁与铆钉头间的承压能力决定；此外，笛卡尔连接器单元Cartesian Connector可精确模拟出不同板厚比下锁铆连接的荷载-变形曲线和抗剪性能指标，且计算精度和效率较高，在冷弯薄壁型钢结构的非线性有限元分析中优先考虑。

5 结束语

采用等效面域偶合、约束单元、连接单元三大类8种简化方法建立了锁铆连接受剪时的非线性有限元分析模型，对比分析了简化模拟结果与试验结果，探明了各简化模型的适用范围，完成了不同板厚比的冷弯型钢锁铆连接参数分析，提出了适合冷弯型钢锁铆连接的抗剪性能有限元简化分析方法，研究结果表明：

1)板厚比t2/t1是影响锁铆连接抗剪性能和破坏模式的关键因素。当t2/t1<1.5时，锁铆连接发生铆钉腿拔出下层钢板破坏，其受剪承载力由锁铆连接区域内紧固机构的受剪性能决定，并随钢板总厚度的增加基本成线性增加；当t2/t1≥1.5时，锁铆连接发生铆钉头剪脱上层钢板破坏，其受剪承载力由上层较薄钢板孔壁与铆钉头间的承压能力决定，并随上层钢板厚度的增加而增加。

2)等效面域耦合简化方法的有限元模型仅适用于研究锁铆接头局部的力学性能；约束单元Pin和紧固件单元Fastener仅适用于模拟未达到破坏阶段的锁铆连接的力学性能，而约束单元beam则不适用于锁铆连接的非线性简化模拟。连接器单元Cartesian Connector与弹簧单元Spring2适用于研究锁铆连接构件的整体受力性能，且两者相比，连接器单元Cartesian Connector的计算效率和精度更高。

3)对于冷弯薄壁型钢结构中连接的非线性有限元简化分析，龙骨框架中构件间的锁铆连接可采用约束单元Pin或紧固件单元Fastener进行简化模拟，龙骨框架与钢面板间的锁铆连接可采用连接器单元Cartesian Connector或弹簧单元Spring2进行简化模拟。

4)笛卡尔连接器单元可精确模拟出不同板厚比下锁铆连接的荷载-变形曲线和抗剪性能指标，且计算效率较高，在冷弯薄壁型钢结构的非线性有限元分析中优先考虑。