X型圆钢管相贯节点超低周疲劳裂纹萌生寿命预测*

王旭东 黄政华 韩 涵

(贵州大学土木工程学院， 贵阳 550025)

0 引 言

圆钢管相贯节点具有构件连接方便，造型美观等优点，近年来在机场和大型体育场馆等大跨度结构中得到了广泛应用[1]。但是随着钢结构建筑跨度和高度的不断增加，结构设计日益复杂化，有关钢结构的破坏事故频繁发生，特别是在罕遇地震作用下，相贯节点经历较大的塑性变形，并在循环次数较低的情况下(一般低于20周)，裂纹在构件或焊接节点内萌生并扩展，最终发生超低周疲劳破坏。韧性断裂是钢结构的重要破坏形式之一，所以准确评估韧性断裂是评估结构在地震等极端荷载作用下性能的必要条件[2-4]。

近年来，国内外学者对钢材微观机制断裂预测模型开展了较多的研究，Kanvinde等把孔穴扩张模型推广到超低周循环加载的情况，提出了循环孔穴增长模型(CVGM模型)和退化有效塑性应变模型(DSPS模型)[5-6]。廖芳芳等采用已校准循环空穴扩张模型对钢结构节点进行超低周疲劳断裂预测，预测结果与试验结果相比有较高的精确度，从而得出微观断裂判据对钢结构节点超低周疲劳断裂预测有较好的适用性[7]。为了预测钢结构在超低周疲劳荷载作用下的延性裂纹萌生寿命，国内外学者提出了多种考虑延性损伤和疲劳损伤综合影响的预测模型，Tateishi进行了低周疲劳试验，提出了引入损伤力学概念的简单模型，作为预测低周疲劳寿命的一种新方法，并检验了该模型的有效性[8]；Xue提出了一种新的寿命预测模型，通过引入指数函数能够得到从超低周疲劳到低周疲劳整个周期的循环寿命，利用现有文献的试验数据，证明了所提出的表达式对几种多晶金属的适用性[9]；Ge等提出基于塑性应变幅的损伤累积模型，通过对9组厚壁钢柱进行循环加载试验，验证了该模型对延性裂纹萌生的预测具有较好的准确性[10]；Kang等采用不同模型对钢桥墩在超低周疲劳荷载作用下的裂纹萌生寿命进行预测，并研究了有限元模型分析中网格尺寸效应对分析结果的影响[2]。

以上模型都是从微观的角度上对结构构件进行超低周疲劳断裂预测，都需要利用有限元软件对节点进行分析，计算工作量大，目前，即使是高性能的计算机，也需要花费大量的计算时间，并不适用于工程设计[1]。对于受到多种几何参数影响的X型圆钢管相贯节点来说，试验存在工作量大、耗时长、费用昂贵等问题，因此数值模拟手段成为解决该问题的重要替代方法[9-11]。本文通过ABAQUS有限元分析软件，并采用自编的VUSDFLD子程序，基于CVGM断裂判据对节点进行延性断裂预测，并对得到的数据进行参数拟合，同时从宏观的角度，将裂纹萌生寿命与加载幅值和节点的几何参数相结合，推导出预测X型圆钢管相贯节点裂纹萌生寿命的经验公式，以供工程设计参考。

1 循环孔穴增长模型(CVGM模型)

Kanvinde等为考虑拉压循环加载过程中应力三轴度的正负情况，将加载过程分为拉伸循环和压缩循环，若应力三轴度为负，在塑性应变下空穴收缩，若为正，则空穴扩张，然后分别积分，将适用于单向拉伸的VGM模型扩展到适用于疲劳的CVGM模型，来预测循环荷载下材料的断裂破坏[6]:

(1a)

(1b)

(1c)

其中T=σm/σe

式中：λCVGM为循环荷载作用下钢材本身的损伤累积退化参数，可通过圆周平滑槽口试件在循环荷载作用下的试验测得；εp为最后一个受拉循环开始时的等效塑性应变；η为单调拉伸试验校准的圆周平滑槽口试件临界空穴扩张指数；T为应力三轴度；σm为静水应力，σe为Mises等效应力；dεt为受拉循环荷载作用下的等效塑性应变增量；dεc为受压循环荷载作用下的等效塑性应变增量。当满足式(1c)时，CVGM判据认为该材料点发生开裂。

2 采用CVGM预测相贯节点断裂的有效性验证

孟宪德等对2个不同几何参数的X型厚壁圆钢管相贯节点进行平面外受弯滞回性能试验[12]，为了验证CVGM模型对相贯节点断裂预测的可靠性和准确性，取文献[12]中的BXH-2试件进行有限元分析。通过ABAQUS有限元分析软件对BXH-2试件进行建模，并采用自编的VUSDFLD子程序对CVGM判据进行编译，当单元材料点满足CVGM判据时就会从模型中删除，以达到能够精准预测节点开裂时刻的目的，并且可以通过单元材料点的删除来模拟节点破坏模式。

图1为试件BXH-2荷载-位移曲线及断裂预测。图中，圆圈为试验断裂位置，三角形为有限元分析CVGM模型预测的断裂位置。由图1可以发现：试验结果和有限元分析得到的结果显示节点均在第10圈发生断裂，试验节点断裂时刻的位移为17.45 mm，断裂时的极限承载力为144.89 kN；有限元分析得到的节点断裂时刻位移为18.94 mm，断裂时的极限承载力为145.65 kN。图2给出了节点破坏模式，对比可以发现将CVGM判据代入ABAQUS子程序中模拟的裂纹扩展路径与试验的破坏模式较为一致，均为主管壁在鞍点处开裂。由以上分析数据和节点破坏模式可以看出有限元分析结果和试验结果比较接近，验证了采用CVGM断裂判据进行有限元分析的准确性。

图1 试件BXH-2荷载-位移曲线及断裂预测Fig.1 Load-displacement curves and fracture prediction of specimen BXH-2

a—裂纹扩展；b—试验现象。图2 节点破坏模式Fig.2 Failure modes of joints

3 试验设计

3.1 节点尺寸及几何参数

圆钢管相贯节点的裂纹萌生寿命与节点的几何参数(腹杆与弦杆的直径比、弦杆的径厚比、腹杆与弦杆的壁厚比、腹杆与弦杆的夹角以及两腹杆的间隙)有关。王伟等指出支、主管壁厚比τ对圆钢管相贯节点性能的影响较小，又考虑到研究对象是正交X型圆钢管相贯节点，因此本文主要从支管与主管管径比β和主管径厚比γ研究X型圆钢管相贯节点在超低周疲劳荷载作用下的裂纹萌生寿命[13]。β的取值范围为0.375～0.675，γ的取值范围为10～15。根据正交设计试验理论，本文设计了9组不同几何尺寸的节点。X型圆钢管相贯节点的几何尺寸如表1所示。

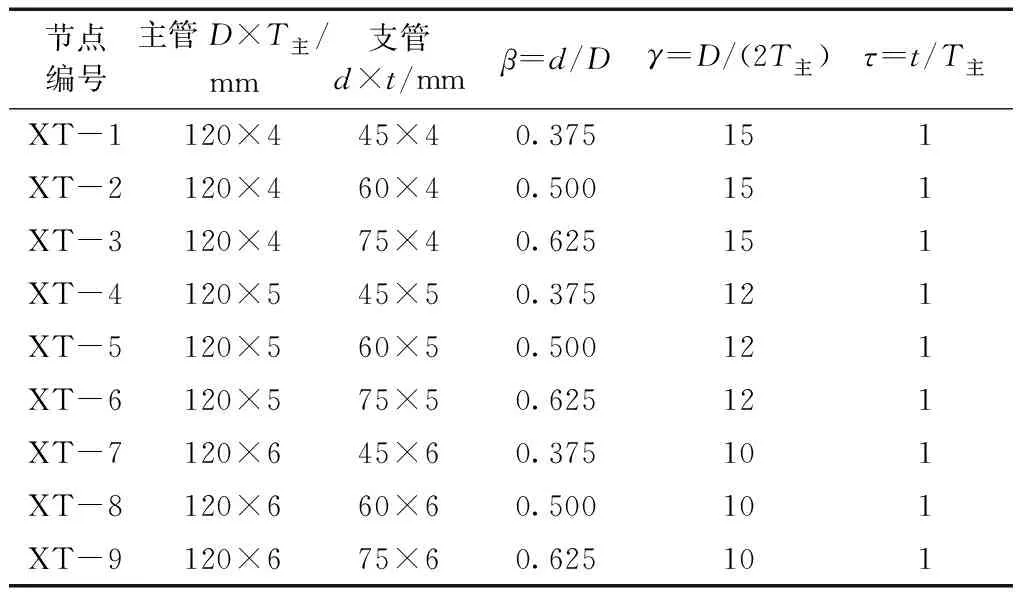
表1 节点几何尺寸Table 1 Geometric sizes of joints

3.2 加载方式

采用在支管端部截面施加对称轴向等幅往复位移的方式进行加载，等幅往复加载幅值的取值范围为2δy～7δy，每个节点共施加11组不同的加载幅值，每组幅值增加0.5δy，如图3所示,其中，n=2.0,2.5,3.0,…,7.0，δy为X型圆钢管相贯节点的屈服位移，其取值由单调荷载加载下的荷载-位移曲线采用Kurobane[14]准则来确定，即在单调荷载条件下的荷载-位移曲线中作过原点且斜率为0.779kN(kN为曲线的初始刚度)的直线，其与曲线的交点所对应的变形即为节点的屈服位移。表2列出了各个节点的屈服位移。

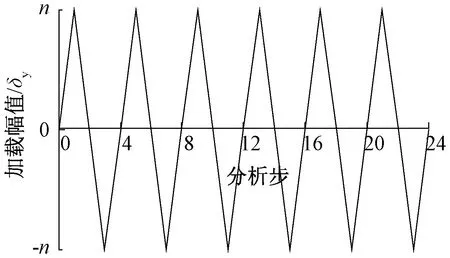
图3 等幅加载示意Fig.3 Equal amplitude loading schematic

表2 各节点对应的屈服位移Table 2 Yield displacement of joints mm

3.3 钢材微观断裂判据参数

本文采用文献[15]中校定的Q345结构钢热影响区的微观断裂参数，见表3。

表3 Q345 结构钢热影响区的微观断裂参数Table 3 Micro fracture parameters of heat affected zone of Q345 structural steel

3.4 有限元建模

采用ABAQUS有限元分析软件建立以上9个节点的三维分析模型，在支管端部截面施加对称轴向位移往复荷载，考虑到节点具有荷载以及结构的对称性，取整体节点的1/8模型进行建模，并在对称面上施加轴对称边界条件，节点主管端部截面施加铰接约束。在建模过程中考虑焊缝，各个节点均采用全周角焊缝，焊脚尺寸hf取1.5倍较小管壁厚度，焊缝处支管与主管管壁间隙为0.5 mm。整体模型如图4所示。

图4 整体模型Fig.4 The overall model

在微观断裂模型中，延性裂纹的萌生不是单一材料点的行为，而是材料临界体积的行为，因此需要建立一个长度尺度以保证能够满足触发韧性断裂的破坏准则，引入特征长度参数l*来描述连续多个材料点达到延性断裂指标。微观力学模型必须在满足特征长度l*上达到判据要求，才认为发生了延性裂纹开展。l*的值取决于材料的微观结构，可以通过扫描电子显微镜得到。子模型网格尺寸确定原则为网格尺寸和材料点特征长度l*的平均值接近，取子模型网格尺寸为0.3 mm，如图5所示。

图5 子模型Fig.5 The submodel

节点采用Q345钢材，材料塑性流动采用混合强化模型来模拟，包含等向强化和随动强化两部分。随动强化钢材的真实应力-应变关系采用廖芳芳文献中对Q345钢材的校正结果[16]，如图6所示；等向强化中所取的屈服应力σ0和材料参数Q∞、b值也采用廖芳芳对圆周平滑槽口试件的往复加载试验和有限元共同校正的结果。焊缝节点域附近采用热影响区钢材，其余部位采用母材金属。泊松比取0.3，弹性模量取206 GPa。

a—母材；b—热影响区。图6 材料真实应力-塑性应变曲线Fig.6 Real stress-plastic strain curves of materials

4 X型圆钢管相贯节点裂纹萌生寿命预测

4.1 裂纹萌生寿命的参数化分析

在低周疲劳状态下，Manson[17]和Coffin[18]指出构件的疲劳寿命与塑性应变幅值之间呈幂函数形式，如式(2)所示：

εp(Nf)k=C

(2)

式中：εp和Nf分别为塑性应变振幅和失效循环次数；k和C为材料常数。

基于Manson-Coffin定律，一些典型的预测模型[8-10]通过修正Manson-Coffin定律关系考虑了延性损伤和疲劳损伤的综合影响。X型圆钢管相贯节点在等幅往复加载方式下的裂纹萌生寿命如表4所示。通过表4中的数据画出节点的裂纹萌生寿命曲线，如图7所示。可以看出:节点的裂纹萌生寿命与加载幅值之间呈幂函数或指数函数关系。根据Manson-Coffin定律和节点裂纹萌生寿命的曲线趋势，本文就此假定X型圆钢管相贯节点的裂纹萌生寿命与加载幅值之间的函数形式为：

表4 X型圆钢管相贯节点裂纹萌生寿命Table 4 Crack initiation life of unstiffened CHS Steel Tube X-joints 周次

图7 节点XT-1、XT-2、XT-3裂纹萌生寿命曲线Fig.7 Crack initiation life curves of joint XT-1, XT-2 and XT-3

Nf=AeBδi+C

(3)

其中δi=δ/δy

式中：A、C为与材料性质本身相关的参数；B为常数，本文中取B=-0.92；δi为加载制度；δ为加载幅值；δy为屈服位移；Nf为裂纹萌生寿命。

通过MATLAB软件对圆钢管相贯节点进行参数化分析得到裂纹萌生寿命的拟合曲线，最终得到的参数拟合公式如下：

XT-1：Nf,1=42.36e-0.92δi+2.003

(4a)

XT-2：Nf,2=60.93e-0.92δi+3.045

(4b)

XT-3：Nf,3=91.26e-0.92δi+4.786

(4c)

XT-4：Nf,4=77.02e-0.92δi+2.242

(4d)

XT-5：Nf,5=102.7e-0.92δi+3.940

(4e)

XT-6：Nf,6=157.0e-0.92δi+6.214

(4f)

XT-7：Nf,7=87.99e-0.92δi+2.979

(4g)

XT-8：Nf,8=109.8e-0.92δi+4.064

(4h)

XT-9：Nf,9=215.9e-0.92δi+7.234

(4i)

节点的裂纹萌生寿命曲线和拟合曲线如图8所示。可以发现：X型圆钢管相贯节点在等幅往复荷载作用下，拟合公式都能较好地预测X型圆钢管相贯节点的超低周疲劳裂纹萌生寿命；随着径厚比γ的增大，相贯节点的裂纹萌生寿命在不断增大；随着支、主管管径比β的增大，相贯节点的裂纹萌生寿命在不断减小；不同几何参数的X型圆钢管相贯节点在低等幅荷载作用下裂纹萌生寿命之间的差值较为明显，在高等幅荷载作用下裂纹萌生寿命之间的差值较小，这是由于在低等幅荷载作用下，节点的等效塑性应变变化速率较慢，且节点的应力三轴度也相对较低，因此对节点的几何尺寸进行较小的改变就能使其裂纹萌生寿命发生较大变化。在对超低周疲劳荷载作用下的构件进行设计时，需要对构件进行严格的分析计算，并对结构构件的性能进行大幅度的提升。

a—γ=15; b—β=0.675。图8 节点的裂纹萌生寿命曲线和拟合曲线Fig.8 Crack initiation life curves and fitting curves of joints

通过9个节点的拟合公式，可以发现参数A、C与节点的几何尺寸之间存在一定的关系。参数A、C与管径比β和径厚比γ之间的关系如图9和图10所示，由图中可以发现，参数A、C的变化趋势大致相同，都随着β的增大而增大，随着γ的增大而减小，通过曲线的形式可以看出参数A、C与β、γ之间呈幂函数或指数函数关系。王伟等通过单参数分析确定各影响参数与节点局部刚度之间的函数形式，从而设定回归模式，并用正交试验设计理论设计计算模型[13]。本文采用相同的方法通过假定参数A、C的函数形式，然后采用MATLAB软件进行拟合，最终得到参数A、C的表达式：

a—A-β关系曲线；b—A-γ关系曲线。图9 参数A变化趋势Fig.9 Variation trend of parameter A

a—参数C与β之间的关系；b—参数C与γ之间的关系。图10 参数C变化趋势Fig.10 Variation trend of parameter C

A=136.8e2.936β-0.154 4γ

(5a)

C=2.006e2.841β-0.076 1γ

(5b)

式中：β为支管与主管管径比；γ为主管径厚比。

将式(5)代入式(3)最终得到了X型圆钢管相贯节点在等幅循环荷载加载下的裂纹萌生寿命公式：

Nf=136.8e(2.936β-0.1544γ)e-0.92δi+2.006e(2.841β-0.0761γ)

(6)

将表1中的节点代入式(6)进行计算并与表4进行比较，结果见表5。可以发现，公式计算值与有限元计算值之间的误差基本都在20%以内，大多数预测结果误差在10%以内，预测结果吻合较好，因此可以认为该拟合公式能够较好地预测X型圆钢管相贯节点在等幅往复荷载作用下的超低周疲劳裂纹萌生寿命。

表5 公式计算值与有限元计算值的比较Table 5 Comparisons between formula calculation resultsand FEA results

4.2 算例验证

为了进一步验证式(6)对预测X型圆钢管相贯节点裂纹萌生寿命的适用性，设计了4个不同尺寸的节点进行有限元分析，各个节点的几何尺寸如表6所示,等幅往复加载幅值取5δy。

表6 节点几何尺寸及参数Table 6 Geometric dimensions and parameters of joints

采用CVGM断裂判据对各个节点进行断裂预测，有限元预测结果与公式计算结果如表7所示。

表7 有限元与公式预测裂纹萌生寿命的结果Table 7 Prediction of crack initiation life by FEA and formula 周次

可以发现：公式预测结果与有限元预测结果的差值均在1圈以内，且公式预测的趋势与有限元预测的趋势相同，可以认为该公式具有一定的准确性；本文得出的式(6)对主管直径不是120 mm的X型圆钢管相贯节点也同样适用。在对X型圆钢管相贯节点进行节点设计时，可以用该经验公式选择疲劳寿命高、抗震性能更好的节点形式。

4.3 超低周疲劳荷载下裂纹萌生寿命预测

Miner指出在随机荷载作用下假设每个加载循环的影响是独立的，损伤指数Di=ni/Nf，其中ni和Nf分别是第i个加载幅值的循环次数和疲劳寿命[19]。在工程实践中，累积损伤指数D在无损状态下等于0，在裂纹萌生时等于1。累积损伤参数D表示如下:

(7)

文中已经给出了等幅往复加载下节点裂纹萌生寿命的预测公式，因此，通过等幅往复加载下节点的裂纹萌生寿命来预测变幅加载下节点的超低周疲劳寿命。采用Miner准则，将式(3)代入式(7)得：

(8)

式(8)即为预测变幅加载下节点的超低周疲劳寿命。为了验证其准确性，按照图11的加载制度，对表1中的圆钢管相贯节点进行有限元分析，根据微观断裂判据CVGM预测节点的开裂时刻，预测过程如图12所示。将有限元预测结果与公式计算得出的裂纹萌生寿命进行比较，结果见表8。可以看出，基于Miner准则，式(8)能够较为准确地预测超低周疲劳寿命的圈数。尽管根据等幅往复加载下的裂纹萌生寿命公式预测变幅加载制度下节点的超低周疲劳寿命存在一定的偏差，但是偏差基本都在5%以内，出现偏差的原因在于拟合的公式与实际真实情况存在一定的误差，并且每个加载循环的影响并不都是独立的，根据拟合的吻合程度，可以认为该种方法是可行的。由于缺乏试验数据，该方法还存在于理论阶段，后续还需要通过试验做进一步的验证。

图11 加载制度示意Fig.11 The schematic diagram of loading system

图12 XT-2节点变幅加载下基于CVGM判据预测开裂Fig.12 Crack prediction based on CVGM criterion under variable amplitude loads of XT-2 joint

表8 有限元基于CVGM判据预测结果和公式预测结果对比Table 8 Comparisons of finite element prediction results based on CVGM criterion and formula prediction results

5 结束语

1)随着支、主管管径比的增大，X型圆钢管相贯节点在超低周疲劳荷载作用下的裂纹萌生寿命在不断减小；随着径厚比γ的增大，X型圆钢管相贯节点在超低周疲劳荷载作用下的裂纹萌生寿命在不断增大。

2)对X型圆钢管相贯节点进行疲劳损伤设计时，对于在超低周疲劳荷载作用下的构件，需要对构件进行严格的分析计算，对结构构件的性能进行大幅度的提升。

3)X型圆钢管相贯节点的超低周裂纹萌生寿命与加载幅值和节点的几何参数之间存在一定的规律。本文通过参数化分析提出了预测X型圆钢管相贯节点在等幅往复荷载作用下裂纹萌生寿命的经验公式(即式(6))。其中，支主管管径比β的取值范围为0.375～0.675，主管径厚比γ的取值范围为10～15，加载幅值δi的取值范围为2δy～7δy，且支主管壁厚比τ为1。该公式基于本文指出的受力工况提出，适用于Q345钢材，是否适用于其他的钢材和受力工况还有待进一步深入研究确定。

4)根据Miner准则，将等幅往复加载下得到的裂纹萌生寿命公式代入累计损伤参数D中，可以较为准确地预测变幅加载下节点的超低周疲劳寿命。