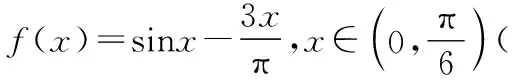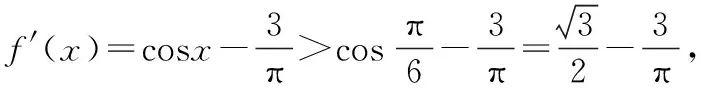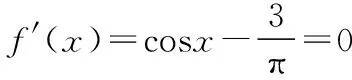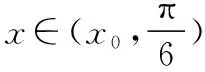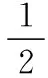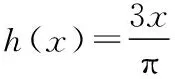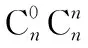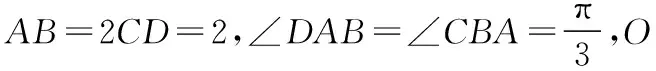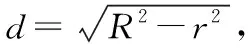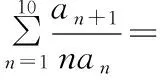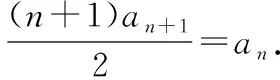转化思想在高中数学解题中的应用探究

江苏 王恩普

(作者单位：江苏省淮阴中学教育集团 淮安市新淮高级中学)

数学思想方法是数学的灵魂及数学学科核心素养的重要内涵，作为数学教学的重要组成部分，不仅能够帮助学生更好地获得解题思路，还能够提高学生的解题能力，发展学生的数学思维，提高学生的数学素养.转化思想作为数学思想的重要组成部分，属于数学思维里的精髓部分，在数学学习过程中，转化思想能够将烦琐、困难和生疏的问题转化为简单、容易和熟悉的问题来解决，是学生在新知识的学习和数学解题过程中不可或缺的重要思想，文章将从以下几个角度谈谈转化思想在高中数学解题中的应用.

1.数形转化，发展学生直观素养

数形转化是将抽象的数学语言与直观的图形结合起来，通过建立数与形之间的联系，使抽象的数学直观化、复杂的问题简单化、表面的问题理性化，让学生的思维更加敏捷、灵活，更有判断力，更具深刻性，不仅能够发挥学生的想象力，提高学生的思维能力，更有助于学生把握数学问题的本质，提高思维能力和数学素养.

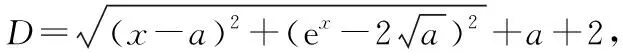
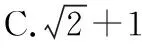
分析：初看此题，如果从函数的角度出发，会发现问题很棘手，就算是运用导数工具，也无从做起，因此要学会换个角度，从“形”的角度也就是几何意义上寻求突破.

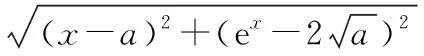
评注：本题中，从函数角度的“复杂”到几何意义角度的“直观”，完美体现了数形转化的优势所在，也更容易感悟到问题的本质.

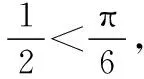
A.c

C.a

且当x∈(0,x0)时，f(x)单调递增；

在同一坐标系里画出两个函数的图象：

评注：本题是比较大小问题，直接比较有难度，同时构造函数不太明显，通过发现一些隐性条件构造出函数以后，研究又遇到了困难，由于同时涉及三角函数与一次函数，无论是借助放缩，还是隐零点代换，都不易处理，而如果同时在坐标系中画出两个函数的图象，问题便迎刃而解了，充分体现了数形转化思想的美妙.

2.模型转化，提升建模意识

数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学方法构建模型解决问题的核心素养，在平时的学习过程中，除了建立数学模型来解决实际问题，也要能够借助于一些特定的、熟悉的数学模型解决数学问题，甚至，还可以把常规的数学问题转化为实际模型来解决，进一步促进数学建模素养的提升.

分析：该题源自苏教版2019选择性必修第二册82页问题与探究，在探究中给出的解释是从“算两次”的角度进行研究，可以引导学生继续探索，同时培养学生探究的兴趣，但是如果“算两次”方法的介绍，学生不易想到，而如果把组合数恒等式与实际模型联系在一起，问题会变得格外亲切，同时又易于理解.

解析：根据题目的特点，左边是组合数的平方，也就是组合数的乘积，我们可以构造取球模型，而乘法可以构造相互独立事件同时发生的情况，于是建立如下模型：

一个盒子中有2n个球，白球n个，黑球n个，那么从中取出n个球共有多少种结果？

方案一：

方案二：

我们可以把取出的n个球进行分类：

…

评注：数学建模作为数学六大核心素养之一，在数学学习过程中显得尤其重要，而构造实际模型来解决数学问题既可以轻松的解决问题，又避免了一些可能遇到的烦琐的运算过程，同时培养了学生的建模意识.如果能够坚持带着这样的思维来思考问题，尤其是主动建模的意识，定会促进数学实践能力和创新意识的发展，从而感悟数学的应用价值.

评注：平面截球的模型在立体几何中是必须掌握的基础知识，学生掌握的相对较少，但是得分结果告诉我们，如果把该模型放在一个具体的情境中，或许会把问题考虑的相对复杂，相反，如果能够把问题转化为基本的常见模型，问题的解决将起到事半功倍的效果.

3.逻辑转化，增强思维创新

在现阶段高中数学学科的教学中，学生逻辑思维的培养至关重要，不仅有助于学生知识理解能力和运用能力的提升，同时也有助于学生在数学学科的良好发展.在具体的问题解决过程中，不仅要学会有逻辑的思考问题，还要注重逻辑的严谨性，更为重要的是在逻辑思考的基础上能否有创新.

【例5】设A∪B∪C={1,2,3,4,5,6}，且A∩B={1,2}，{1,2,3,4}⊆(B∪C)，则符合条件的(A,B,C)共有多少组.

分析：本题源于一道竞赛辅导题，从常规角度出发，要对题中的集合A，B，C进行分类讨论，分的情况比较多，而且在每一类中还要细分，学生很难通过分类讨论得出正确答案，具体过程这里不再给出，读者可以自行讨论.

解析：如图首先将集合A，B，C相交于7个区域，分别记为a，b，c，d，e，f，g可以尝试将题目条件看作把六个数字填入集合中有多少方法.

首先，1，2，只能放在b或e中，有2×2=4种，

然后，根据{1,2,3,4}⊆B∪C可知，3和4不在b和e中，可能在c，d，f，g中，

有4×4=16种，

最后，根据A∪B∪C={1,2,3,4,5,6}可知，5和6不在b和e中，可能在a，c，d，f，g中，有5×5=25种，

由分步计数原理可得一共有4×16×25=1 600种，即符合条件的(A,B,C)共有1 600组.

评析：本题通过转化逻辑的顺序，避开了正面多而繁杂的讨论，并不因为集合背景的增加影响排列组合的主线，借助于分步计数原理，使得解题思路变得非常清晰，自然.

4.联想转化，促进知识迁移

解题是对已学内容的综合运用，涉及概念、定理、公式、技巧、方法等，如何将相关内容联系在一起是门学问.数学解题的思维过程实质上是已知和未知之间的一系列联想过程，其中联想思维就是要能见微知著，展开想象，联系有关的或是无关的各种内容，然后得出相关结论.据心理学研究发现，善于联想思维的人们，学到的知识在他们的头脑里组成有机的网状，相互联系在一起，而不是相互独立的，更不是孤立割裂的.所以我们要自觉地发挥大脑的联想思维功能，通过联想进行转化达到融会贯通.

分析：刚接触到题目，很难想象e2x会用多项式来表示，如果粗略的搜索教材中学习过的内容，好像没有涉及，但其实在教材的三角函数习题中曾经介绍过sinx,cosx的泰勒展开式，但是没有给出如何研究，面对这样的形式，我们该如何处理多项式系数呢？仔细观察，对于展开式，可以联想到学习过的二项式定理中的展开式的项的系数的几种方法，经过筛选，发现借助于导数与赋值可以解决.

解析：对于第一问，在恒等式e2x=a0+a1x+a2x2+…+anxn+…中，令x=0，可得a0=1，然后对恒等式e2x=a0+a1x+a2x2+…+anxn+…两边求导，可得

2e2x=a1+2a2x+…+nanxn-1+(n+1)an+1xn+…，

则有

评注：作为高观点下的泰勒展开式，高中教材中没有具体提及，那么遇到以泰勒展开式为背景的问题时，需要及时联想到学习过的二项式展开式，借助于二项式展开式中项的系数的方法，不仅使问题得到解决，还促进了知识与方法的迁移.

5.结语

在高中数学教学中，会遇到各种各样的数学问题，转化思想是解题中经常用到的，教师应该明确转化思想的应用原则，借助于数形转化、模型转化、逻辑转化、联想转化等方式，在实际的教学题中积极的渗透转化思想，促进学生素养的提升，让他们学会用数学眼光观察世界，用数学思维思考世界，用数学语言表达世界.