完善数学思维模式 提升解题研题能力

四川 王昌林 罗萍双

(作者单位：四川电影电视学院实验中学)

思维能力是各种能力的核心，想要提升考生解题研题能力，数学思维的培养与完善就显得尤为关键.本文介绍构造与逆向两种思维模式的应用，然后以案例分析的形式呈现一题多解、一题多变以及归纳总结的解题研题具体步骤，最终使学生解题研题能力得到提升.

一、数学思维模式

数学思维模式是指主体在数学思维活动中形成的相对稳定的思维模式，是数学模式在主体头脑中概括并加工的反映.因此数学思维模式是一定的数学知识结构与数学思维方式结合而成的动力系统.数学思维模式的种类繁多，常见的有化归、构造、逆向、类比联想、数形结合、函数与方程等，以下是构造与逆向两种思维模式的简单应用.

(一)构造思维模式

类型1 构造函数

构造函数是指根据题目设对象，通过构造一种新的函数关系并利用所构造函数的性质解决问题.要理解和掌握构造函数的要点，掌握常见函数模型的图象和性质.构造函数思想有助于实现数学从常量到变量的认识飞跃.

(1)略；(2)若曲线y=f(x)与直线y=1有且仅有两个交点，求a的取值范围.

类型2 构造图形

构造图形是指在解决某个数学问题时，根据问题的内部联系以及数量特征，构造出与之相对应的几何图形或函数图象.一般来说，代数问题都较为抽象，若是能够通过构造的方式，将其合理的转化为几何问题，利用数形结合这一重要数学思想，往往可以增强问题的直观性，使得解答过程事半功倍.

【例2】已知集合A={(x，y)|x2+y2≤3，x∈Z，y∈Z}，则A中元素的个数为__________.

类型3 构造与运用模型

求解某些数学问题时，针对问题的背景、结构与特征，在直接求解存在较大困难时，通过观察和联想，恰当地构造出熟知的数学模型.通过研究该数学模型来解决问题，这是构造与运用模型的思想方法，是一种十分有效的解题策略.同时，构造的过程是对数学基础知识掌握熟练与否的具体表现，也是一种创新思维的过程和数学学科核心素养的体现.

(1)求E的方程；

(2)证明：直线CD过定点.

评析：例3所考查的是圆锥曲线中的定点类问题，也符合极点、极线模型的使用条件，即一个四边形的四个顶点在一条二阶曲线上，并且四边形对边不平行，则这个四边形的对边延长线的交点及其对角线所组成的三角形的任一顶点是其对边的极点.虽极点、极线模型不能直接作为解答过程，但可以让考生明确解答方向，合理构造和运用数学模型，既能增强解题效率，又能有效增加考生解答试题的自信.

(二)逆向思维模式

二、解题研题案例分析

对于数学试题的研究，既需要横向的多角度研究，也需要纵向的多层次研究；既需要着眼于宏观层面的研究，如命题理念和原则的研究，也需要着眼于微观层面的研究，如一道试题的研究.其主要内容有：试题的分析、评价与赏析；试题的“一题多解”与“多题一解”；问题的变式、推广；试题的创作与改编；试题的答题技巧与应考对策等.学生受自身限制，可将解题研题的过程简化为“解—变—结”三步骤，即对试题一题多解、一题多变与归纳反思，最终实现做一道题会一类题.

答案：C

评析：本题为双动点下的向量数量积最小值问题，是成都市2021年第三次诊断考试文科选择压轴.在高考题中，与其类似的有2018年上海卷第8题，天津卷第8题，2020年天津卷第15题等.案例有所不同的是定长线段AB是在圆上运动，而不是在直线上运动，例5更具有可研究性.

(一)一题多解，探寻方法拓视野

视角1：基底法

解法1：如图2，取线段AB的中点M，连接PM.

因为点M的轨迹方程为x2+y2=1，所以易得PM的最小值为2，

视角2：坐标法

解法2：设点A(x1，y1)，B(x2，y2)，取线段AB的中点M，设点M(x0，y0).

则x1x2+y1y2=-2，

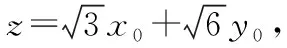
解法3：因为点A与点B皆是圆x2+y2=4上的两个动点，

设A(2cosθ，2sinθ)，B(2cosα，2sinα)，

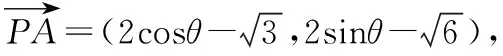
视角3：公式法

当且仅当|PA|=|PB|时取等号.

视角4：极化恒等式法

因为点M的轨迹方程为x2+y2=1，所以易得PM的最小值为2，

视角5：向量中值定理法

因为点M的轨迹方程为x2+y2=1，易得PM的最小值为2，

评注：一题多解的最终目的是为了达到完善知识结构，养成多角度看问题的习惯.向量数量积最值问题多数学生仅会用公式法，偶有学生借助极化恒等式，例5的解答以5种视角入手，可以有效拓展学生看待问题的视野，让学生明白原来向量数量积最值问题的解答也可以是多种多样的，从而引导学生继续研究问题.

(二)一题多变，提升维度促深思

变式1：结构变式

答案：8

变式2：条件变式

变式3：问题变式

变式4：结论变式

答案：是定值，其定值的大小由点P的横纵坐标决定

评注：例5中的动点坐标恰好是基于等边三角形所设的，因此，将线段AB为边长构造圆内正三角形又会发生怎样的变化呢？因此对例5进行以上变式.试题的变式是指通过变式把已有试题变成多个试题.试题变式有利于完善学生的认知结构.一个好的变式是值得玩味的，更是能够启迪思维的.

(三)归纳总结，分析得失谋发展

对于例5中的5种视角，坐标与基底的视角是较为容易想到的，也是解决向量数量积问题的常用方法，合适的基底选取以及建立适当的平面直角坐标系可以起到简化运算的作用，不然只会增大运算与思维量.例如：

解题研题匆匆忙忙，只求数量，不重归纳总结，往往事倍功半.我们可以在总结归纳过程中理解知识点的内涵、外延以及解题技巧；在总结的过程中汲取经验与教训，从而巩固与扩大解题研题成果；最终做到举一反三，解题研题效果也会事半功倍.