与球有关的综合问题探究

江苏 陈 敏 张启兆

(作者单位：无锡市第六高级中学 无锡市青山高级中学)

与球相关的综合问题是近年高考命题的热点之一，而球与几何体的切、接、截问题是与球相关的综合问题中常见的题型，从“几何作图”和“分析图形”两个角度考查直观想象核心素养，考查考生的空间想象能力和推理论证能力，同时考查数学抽象、逻辑推理、数学建模、数学运算等数学核心素养，也是考试的难点.下面谈谈与球有关的综合问题的解题方法与策略.

1.补形法，转化为熟悉模型

全国卷一直注重对球体的考查，尤其是和其他几何体的组合，涉及切、接、截时相关的计算问题，求解这类问题时，要善于将问题向熟悉的问题转化，往往可以通过补形将球体放置在更为特殊的几何体中研究，实现复杂问题简单化.

与球有关的切、接问题中，有以下常用结论：

图1

图2

图3

(2)正四面体的外接球与内切球的半径之比为3∶1.

【分析】先画出图形，如图，由题意可知，利用条件直接求解a，难度较大，但此四面体的对棱相等，故该四面体可以通过补形，补成一个长方体，将四面体的外接球问题转化成长方体的外接球问题，从而转化为长方体棱长与其外接球半径之间的关系.设出长方体过一个顶点的三条棱长，由已知求出三条棱长，则a可求.

【规律方法】(1)知识储备：球和长方体切、接问题是最典型的组合体问题，平时多加研究总结，吃透处理这类问题的方法;

(2)转化意识：当遇到不规则的几何体与球切、接问题时，多联想发散，不规则的几何体从哪来？通过空间想象，找到它的源，尝试将其置在规则的几何体中认知，问题便不难解决;

(3)方法技巧：如果一个三棱锥的三对对棱长度分别相等，则可将其置于长方体中，使其四个顶点分别位于长方体的顶点上，六条棱分别位于长方体的六个面对角线上，即“对棱相等”模型.

【易错提醒】(1)不注重积累，缺乏对常见基本组合体的认识和研究，让转化无“源”；

(2)没有厘清原组合体的点线面之间的关系，在补形时张冠李戴，补错形.

【分析】首先要根据题意准确作出图形，根据该三棱锥底面△ABC的各边长及中线长特征，将下底面补形成平行四边形ABO1C，且O1为△ABC的外心，三棱锥V-ABC外接球的球心必在VO1上.

【规律方法】(1)补形法适用于特殊的棱锥;

(2)若三棱锥具有三条棱两两垂直或三个平面两两垂直的特征，应用数学建模，构建“两两垂直”模型，即“墙角”模型，如图所示，将三棱锥放入伴随长方体中，将棱锥的外接球转化为长方体的外接球，不用找出球心的具体位置，这是处理此类问题的简洁途径.也可以推广到直四棱柱;

(3)对于一侧棱垂直于底面且底面是非直角三角形的四面体的外接球半径问题，可以将四面体补形，补成直四棱柱(或直六棱柱)，使得三棱锥的各个顶点与直四棱柱(或直六棱柱)的顶点重合，因为它们的外接球相同，故可利用直四棱柱(或直六棱柱)的外接球半径公式求出三棱锥的外接球半径.

【易错提醒】注意联系三棱锥的棱长和位置特征，识别三棱锥类型，找准球的直径和三棱锥关联的棱长，以防错位.

【教学建议】重视识图、作图和用图，乃至变换图，提升空间想象能力.球和几何体切、接、截问题，旨在考查学生的空间想象能力.问题往往始于构图，我们更要借助于图形，行于识图、通于析图、善于变图、止于用图.要引导学生有意识地亲自动手作图，提高识图、辨图、画图、用图、变图的能力.解题时，题目中时常无图，要启发引导学生发挥空间想象能力，构造出空间图形，甚至于要在大脑中思考、想象，尝试猜想点、线、面位置关系，然后正确地作出直观图形，进一步求解问题.

2.空间问题平面化

由于“球”是“圆”在空间概念上的延伸，所以研究球的性质时，应注意与圆的性质类比.球的轴截面是大圆，它几乎含有球的全部元素，所以有关球的计算，往往可以作出球的一个大圆，化“球”为“圆”来解决问题，把空间问题转化为平面问题.

【分析】(1)本题没有给出图形，其实质是要考查学生的空间想象能力和作图能力，所以要准确画出图形(如图4)；

(3)将图4绕棱BC所在直线顺时针旋转90°(如图5)，再瞧瞧，问题变得更“容易”.

【解】如图4,

图4

图5

取B1C1的中点为E，BB1的中点为F，CC1的中点为G，

因为∠BAD=60°，直四棱柱ABCD-A1B1C1D1的棱长均为2，

所以△D1B1C1为等边三角形，

又四棱柱ABCD-A1B1C1D1为直四棱柱，

所以BB1⊥平面A1B1C1D1，所以BB1⊥D1E，

因为BB1∩B1C1=B1，所以D1E⊥侧面B1C1CB，

设P为侧面B1C1CB与球面的交线上的点，

则D1E⊥EP，

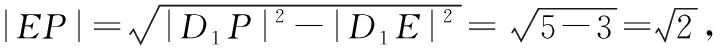
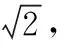
【小贴士】横看成岭侧成峰，远近高低各不同，变换角度，找准适合个人视角习惯的图形，能让问题更“容易”.

【例4】(2020·新高考Ⅰ卷·4)如图，日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O)，地球上一点A的纬度是指OA与地球赤道所在平面所成角，点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷，若晷面与赤道所在平面平行，点A处的纬度为北纬40°，则晷针与点A处的水平面所成角为( )

A.20°B.40°C.50°D.90°

【分析】将题干所涉及的条件在图中“翻译”出来，通过空间想象将日晷晷针与点A处的水平面所成的角转化成线线所成的角，进而实现立体问题平面化的目标，再运用平面几何知识求解.

【解】画出截面图，如图所示，其中CD是赤道所在平面的截线.

l是点A处的水平面的截线，由题意可得OA⊥l，AB是晷针所在直线.m是晷面的截线，由题意晷面和赤道面平行，晷针与晷面垂直，

根据平面平行的性质定理可得m∥CD，

根据线面垂直的定义可得AB⊥m，

由于∠AOC=40°，m∥CD，

所以∠OAG=∠AOC=40°，

由于∠OAG+∠GAE=∠BAE+∠GAE=90°，

所以∠BAE=∠OAG=40°，即晷针与A处的水平面所成角为∠BAE=40°，故选B.

【规律方法】(1)处理与立体几何有关的应用问题时，要厘清实际背景下的条件，设法用立体几何中的点线面的位置关系和数量关系来准确刻画，实现数学化目标；

(2)统筹条件，在图中标注出已知条件，寻求条件间的桥梁，尽量将条件转移至某一平面中处理，进而实现立体问题平面化，在平面中再进一步解答.

【易错提醒】球和几何体切接问题，在审题上多思考，舍得花时间，俗语说得好“磨刀不误砍柴工”，厘清问题的来龙去脉，问题就能解决一大半.

3.找球心(勾股定理法)

【例5】(体积问题)(2021·全国甲卷理·11)已知A，B，C是半径为1的球O的球面上的三个点，且AC⊥BC,AC=BC=1，则三棱锥O-ABC的体积为( )

【分析】先确定所在的截面圆的圆心O1为斜边AB的中点，然后在Rt△ABC和Rt△AOO1中，利用勾股定理求出OO1，再利用锥体的体积公式即可求解.

【解】如图，因为AC⊥BC,AC=BC=1，所以△ABC为等腰直角三角形，

所以△ABC所在的截面圆的圆心O1为斜边AB的中点，

OO1⊥平面ABC.

故选A.

【规律方法】结论1：正方体或长方体的外接球的球心是其体对角线的中点.

结论2：正棱柱的外接球的球心是上、下底面中心连线的中点.

结论3：直三棱柱的外接球的球心是上、下底面三角形外心连线的中点.

方法技巧：勾股定理法的关键是找球心，球心一定在过底面的外心与底面垂直的直线上，画出截面图，构造与半径R有关的直角三角形.

【教学建议】注重知识的积累，构造模型，提升转化能力.球和几何体的切、接、截问题看似复杂，实质可以化归与转化为几种常见模型，平时的学习中，只要我们善于梳理和积累，掌握各种模型问题的处理策略，便可以以不变应万变，另外，在处理这类问题时心中时刻要有一种意识，即“降维”思想，将三维向二维转化，实现立体问题平面化，转化为平面几何问题来处理.

4.体积分割法

【例6】某四棱锥的底面为正方形，顶点在底面的射影为正方形中心，该四棱锥内有一个半径为1的球，则该四棱锥的表面积的最小值是( )

A.16B.8C.32D.24

【分析】由题意知该四棱锥是正四棱锥，在正四棱锥P-ABCD中，设底面正方形的边长为2a，高为h，由题意可知半径为1的球是正四棱锥P-ABCD的内切球时，该四棱锥的表面积最小，利用等体积法求出a与h的关系，再将四棱锥的表面积表示成关于h的函数，再由基本不等式求解即可.

【解】因为四棱锥的底面为正方形，顶点在底面的射影为正方形中心，所以四棱锥P-ABCD是正四棱锥.

如图，当半径为1的球是正四棱锥P-ABCD的内切球时，该四棱锥的表面积最小，设正方形ABCD的边长为2a，AC∩BD=O，连接PO，则PO⊥平面ABCD，所以正四棱锥P-ABCD的高为PO，设PO=h，正四棱锥P-ABCD的表面积为S，

设t=h-2>0，可得h=t+2，

【规律方法】结论1：内切球球心到多面体各面的距离均相等，外接球球心到多面体各顶点的距离均相等.

结论2：正多面体的内切球和外接球的球心重合.

结论3：正棱锥的内切球和外接球球心都在高线上，但不定重合.

方法技巧：体积分割法是求内切球半径的常用方法.

5.解析法

球和几何体的切、接、截问题，重点考查空间想象能力，涉及点、线、面的位置关系及数量关系，运用综合几何法，将空间问题平面化，“一作、二证、三求解”的步骤，把角和距离的计算化归为三角形的边角关系进行求解要求较高，若几何体相对规则，运用向量坐标法，建立恰当的空间直角坐标系，化为空间向量的坐标运算求解，便可以以计算代替推理，降低思维难度.

【例7】(表面积问题)在三棱锥P-ABC中，PA⊥平面ABC，∠BAC=120°，PA=AB=AC=2，若该三棱锥的顶点都在同一个球面上，则该球的表面积为________.

【视角1】求该球的表面积，就是要求球的半径，本质是在空间中找到一点M，使得点M到三棱锥的四个顶点距离相等，再基于该三棱锥，建立恰当的空间直角坐标系，就能通过设坐标，根据几何特征建立方程组，方程获解，问题便迎刃而解.

A(-1,0,0)，P(-1,0,2)，设球心为M(x,y,z)，于是有MA=MB=MC=MP，则

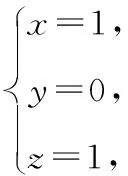
则R2=22+12=5，表面积为4πR2=20π.

【评注】在利用解析法中，关键在于选准坐标系，正确写出坐标，建立方程.

【视角2】在本题中，如果∠BAC=90°，那么我们就可以借鉴上面的第1种方法：补形，将三棱锥补成长方体，将三棱锥与球的问题转化为长方体与球的问题，但是本题中∠BAC=120°，不方便补成长方体，于是联想到把下底面补成正六边形，从而把上述三棱锥补成正六棱柱，如图，把三棱锥与球的问题转化为正六棱柱与球的问题.根据正六棱柱的对称性，于是得到下面的解法2.

解法2(补形法)：该三棱锥可以通过补形补成一个正六棱柱，如图所示，

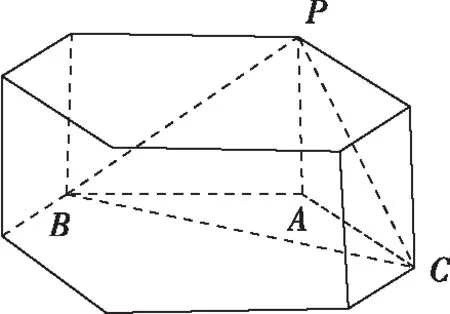
【评注】本题探究了三种方法：解析法，补形法(转化为特殊的几何体与球相接问题)，找球心(转化为平面图形问题处理)，通过上述几种方法比较，我们可以选择、优化解决立体几何中特别是几何体的接切问题的方法.

【规律方法】利用向量法求解球和几何体切接问题时：

(1)选好基底或建立空间直角坐标系是后续解题的前提；

(2)多从方程结构把握方程特征，注意整体思想化简和求解方程.

【易错提醒】因点、线、面位置关系不够清晰，导致空间点的坐标出错.

【教学建议】发散思维，多方认知，优化解法，提高解题能力.处理球和几何体切、接、截问题的核心在于将立体问题转化为平面问题，在具体求解时，首先可以放眼整体观察，将问题置在“大背景(补形)”下认识，有了“靠山”就容易求解了；其次，当问题要求空间想象能力相对较高，不易联系各种条件时，可以考虑可否放在空间直角坐标系下处理，化立体中的推理过程为代数运算过程，平时要从不同角度解决问题，积累经验，以便在解决新问题时，根据具体条件因地制宜，灵活选择使用方法，提高解题能力.