采摘机械臂自适应输入整形控制研究

刘德馨 ,张建成 ,李 媛 ,方建军

(1.北京联合大学机器人学院,北京 100101;2.北京联合大学城市轨道交通与物流学院,北京 100101)

1 引言

农业装备从机械化到智能化的跨越正在加快,农用采摘机器人的应用也越来越广泛.在鲜食蔬果中,番茄是采摘难度最大的果蔬种类之一.番茄果实密集生长相互触碰,且果皮柔软易破,因此夹剪一体式采摘机器人成为了主流.采摘作业时,末端执行器接触到番茄穗所在主枝干后,并拢夹住切断果茎,而后运输到指定位置.但在移动过程中,往往发生果实的掉落问题,其中果穗的抖动,是掉落的重要原因之一.因此,如何抑制果穗运输过程中的抖动,是提高采摘成功率的关键[1–2].

输入整形(input shaping)作为一种前馈控制方法,能实现柔性结构的振动抑制.上世纪50年代,伯利克大学Smith在悬垂物的移动实验中,发明Posicast控制方法消除残余振动.90年代中期,麻省理工学院的Singer等[3]学者改进了这种方法,并将之称为输入整形技术.其后,国内外专家学者对输入整形器的研究相当活跃,并取得了丰硕的成果.文献[4–6]把输入整形从单输入单输出系统,扩展到多输入多输出系统.文献[7]在闭环回路中加入Smith预测器,克服输入整形器造成的时间延迟;文献[8]针对汽车生产线中的装配机器人,提出一种鲁棒性较强的整形器,对移动中的车体执行车轮装配任务;文献[9]把输入整形技术应用到医用X光机上,实现零相位误差周期信号的跟踪;文献[10]对一类带有完整约束的双吊车系统进行分析,根据求取的振荡周期设计出合适的输入整形器;文献[11]提出一种基于S型曲线轨迹生成法,实现旋转起重机两级残留摆角的抑制;文献[12]基于输入整形算法针对深海起重机系统提出了一种实时轨迹规划方法,有效抑制了负载摆动;文献[13]通过引入基函数参数化的前馈控制器和输入整形滤波器,消除期望轨迹引入的扰动;

到目前为止,绝大多数输入整形器(如ZV,ZVD,ZVDD)在求取脉冲的作用时间和幅值时,要求精确的数学模型,控制效果对模型参数的变化很敏感[14–18].但在实际应用中,如采摘机器人的柔性负载是变化的,系统随机性强,参数变化较大,设计的整形器不能很有效的消除残余振动.因此,研究参数不精确已知情况下的振动抑制控制器设计方法有着重要的意义.

本文采用自适应输入整形(adaptive input shaping,AIS)算法来解决系统柔性可变负载的振动问题.设置二次型性能指标函数,通过自适应迭代的方式逐步减小性能指标函数的值.根据整形后的输入量和系统输出,在线计算整形器的脉冲幅值和脉冲时间参数,求取最优解.控制算法形成闭环回路,使得输出量的残余振动为零.仿真实验表明,在变负载情况下,自适应输入整形算法具有很好的振动抑制能力,极大的改善了系统的鲁棒性.研究结果在一维数控滑台上进行验证,实验结果显示了所提方法的有效性,获得满意的控制性能.

以下几章将对本文所提出的控制算法进行详细介绍与分析.文章具体安排如下:第2节简述了输入整形控制的基本原理;第3节考虑柔性可变负载的情况,设置二次型性能指标函数,提出一种自适应输入整形控制算法;第4节将控制算法应用于采摘机械臂抓取西红柿果茎的振动抑制中,并针对负载的质量和柔性连杆长度两个可变参数,分3种情况进行对比,验证自适应输入整形控制算法的有效性.

2 输入整形控制

输入整形控制是将系统期望输入和一组不同幅值和时滞的脉冲序列进行卷积运算,得到整形后的输入信号来驱动系统,达到消除系统的振动的目的.

在进行计算时,通常将被控对象简化为典型的2阶阻尼振动系统.设计如下整形器H(s)[15]:

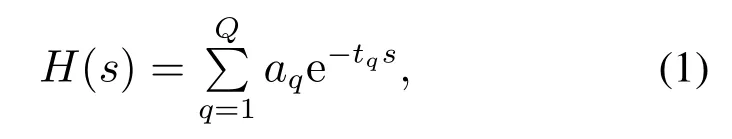
式中:Q为总脉冲个数,aq和tq分别为第q个脉冲的幅值和产生时刻.

在整形器设计时,需要考虑以下基本约束:

1) 残余振动约束条件.

系统在输入整形器的作用下,呈现出有限脉冲响应.即在t≥tQ时刻以后,系统残余振动输出的幅值趋近于0.

2) 脉冲幅值约束条件.

在整形后的输入信号作用下,系统有和原信号相同的输出稳态值.即整形器的脉冲幅值aq的和为1:

3) 时间最优约束条件.

脉冲序列的时长越短,给系统带来的时滞就越短.为提高系统的响应速度,考虑

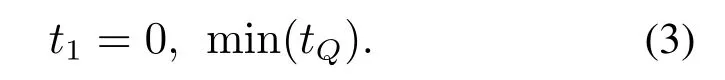
因此,如何求解恰当脉冲幅值a1,a2,···,aQ和脉冲时间t1,t2,···,tQ,是输入整形器设计的核心问题.以经典的两个输入脉冲ZV整形器为例,已知系统的自然角频率ωn和阻尼率ζ.可得到脉冲幅值和时间计算公式:

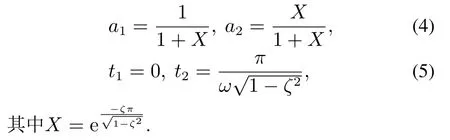
对于ZV整形器,若系统模型求解精确,整形效果非常好,产生的时滞也很短;但当模型求解存在误差时,鲁棒性较差.通过增加整形器的阶数,得到多输入脉冲的ZVD和ZVDD整形器,可以提高抑制系统自然频率或阻尼系统不确定性引起的系统性能下降;但代价是延长了时滞,使得系统响应速度变慢.EI整形器提高系统鲁棒性的方法是在系统频率左右分别选取两个频率值,令这两处余振幅度为零,但不要求在系统频率处的振幅,单峰EI整形器也包含3个脉冲,其时滞和ZVD整形器相同,等于一个振荡周期.

3 自适应输入整形控制

本文采用自适应输入整形(adaptive input shaping,AIS)控制算法,克服由于模型不精确造成的残余振动,增强系统的鲁棒性.

设系统G的原输入为r,在整形器的作用下,整形后的输入为u.考虑添加反馈环节,设置自适应整形器H,根据u和系统的输出y,在线调整H的脉冲幅值和时间.设置二次型性能指标函数,求取幅值和时间的最优解,并赋值给前馈环节,形成闭环控制回路.自适应输入整形算法的结构如图1所示.

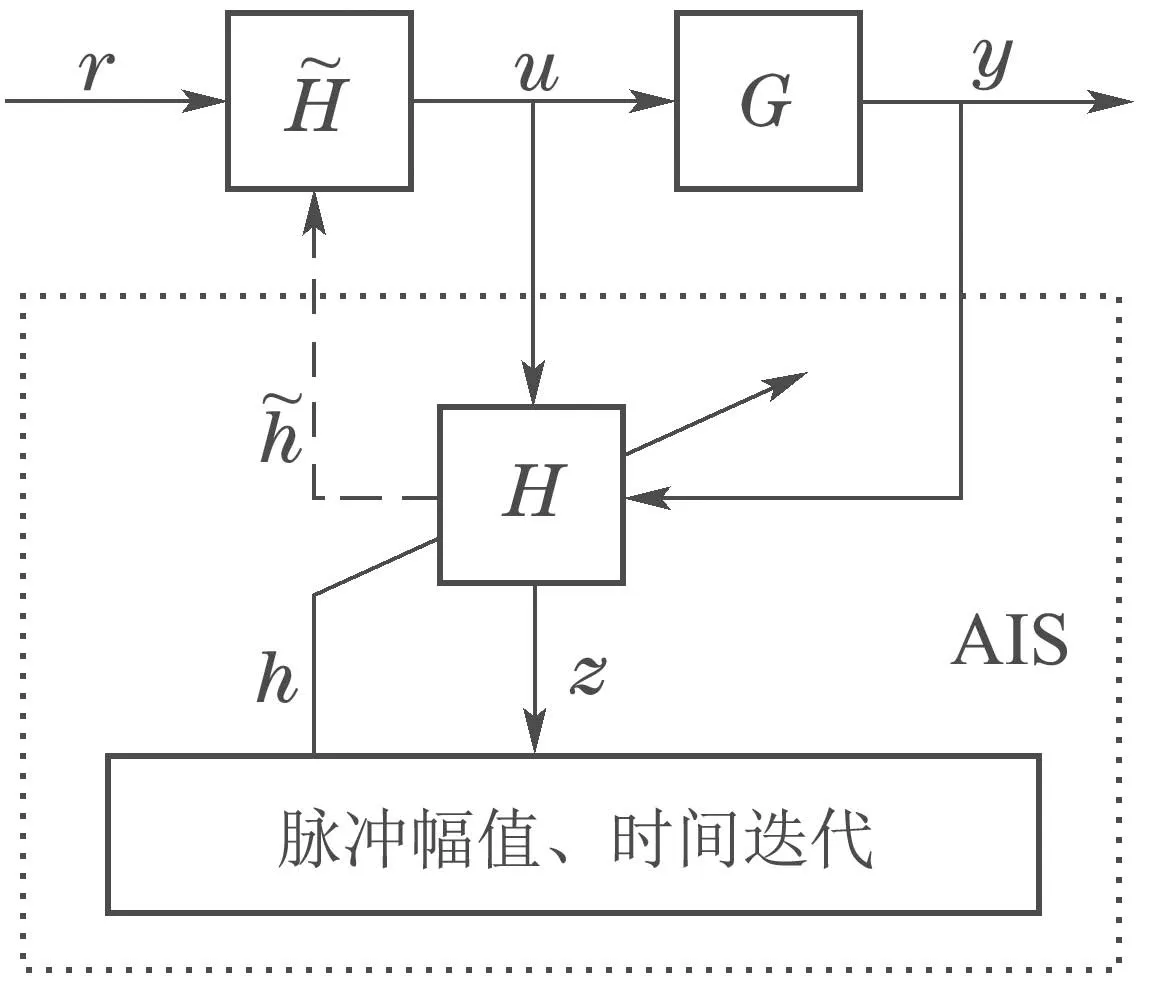
图1 自适应输入整形系统工作原理图Fig.1 The adaptive shaping filter

3.1 问题描述

自适应输入整形算法是通过自适应迭代的方式,在线求解出最优的脉冲序列,使得系统在K次迭代以后,输出值y的残余振动为0.设计自适应整形器H,对输出信号y进行整形,得到z=GHu.由于˜HG=GH,因此迭代算法的目标可转化为寻找整形器H的最优参数,使得GH在输入u的作用下,输出z在K次迭代以后残余振动为0.z的表达式如下:

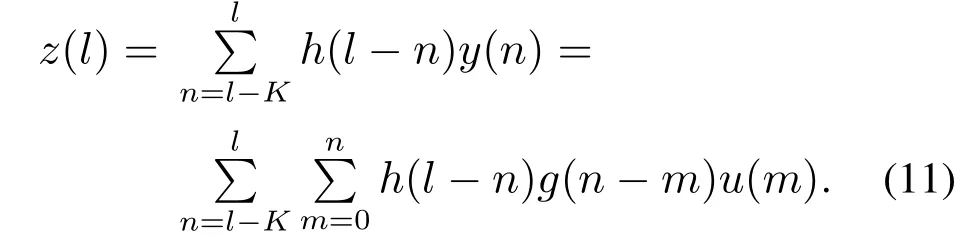
把l时刻的输出值z(l)分为两部分考虑.在输入u的作用下,式(12)中,加号前为GH在0到K时刻的响应叠加值;加号后为K到l时刻的响应叠加值,也就是残余振动.

算法的目的是消除K时刻后的残余振动使得=0.因此,如何根据系统的实时数据,在线求解最优的,使得性能指标函数JN=0,并满足fr=0,是自适应输入整形算法的核心问题.

3.2 自适应输入整形算法推导

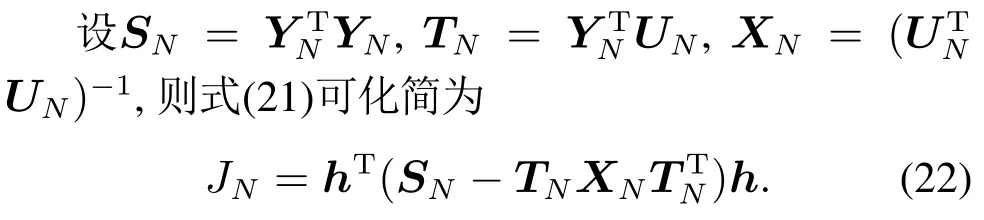
对于第N次迭代,根据系统的输入值u和输出值y,迭代公式如下[5]:

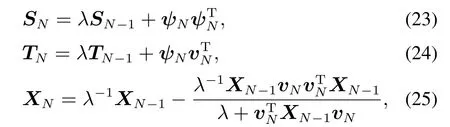
其中:ψN=[y(N)y(N −1)··· y(N −K)]T,vN=[u(N)u(N −1)··· u(N −K)]T,λ<1为遗忘因子.通过式(23)–(25),可根据实时的输入u和输出y迭代计算性能指标函数JN的值,并保证其有界.

进一步需要求解自适应整形器H的最优脉冲序列,本文从最优脉冲幅值和时间两方面分别求解.

3.2.1 最优脉冲幅值

3.2.2 最优脉冲时间

当t中的所有值在K+1个脉冲时间内,不发生改变时,迭代结束,求解出最优脉冲时间值.

4 机械臂柔性负载自适应输入整形控制

4.1 机械臂柔性负载控制系统

为了验证本文提出方法的有效性,以单个西红柿作为负载,西红柿果茎作为柔性连杆,将自适应控制算法应用于采摘机械臂抓取西红柿果茎的振动抑制中.机械臂的结构示意图如图2所示.

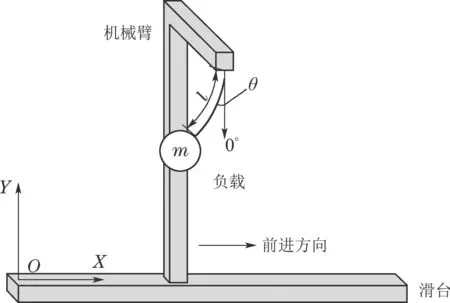
图2 机械臂滑台结构示意图Fig.2 Schematic diagram of robot arm slipway structure

图中,m为负载的质量,l为负载柔性连杆长度,θ为负载的摆角.机械臂振动抑制的目的是使柔性负载沿水平直线方向X从静止状态起步,经过一段匀速运动,到减速停止的过程中,摆角θ尽可能小.

利用拉格朗日动力学对系统进行受力分析,可得出近似线性化的仿真模型:

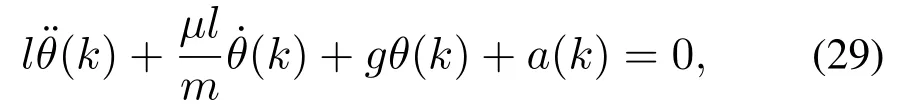
式中:a为机械臂的加速度,µ为负载阻尼.以机械臂加速度a作为系统输入,负载摆角θ作为输出,则系统属于典型的二阶振荡环节,可得到传递函数为

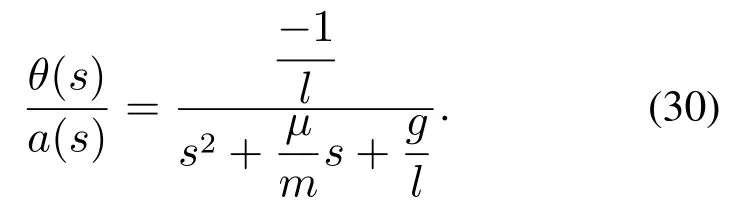
令系统输入a的参考输入r(t)为

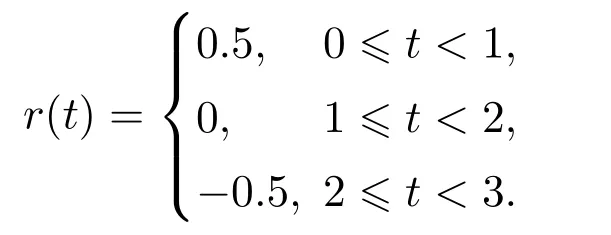
机械臂整个运动过程共耗时3 s,先加速运行1 s,匀速运行1 s,最后减速运行1 s直至停止.则机械臂的加速度a,速度v,位移x轨迹如图3所示.

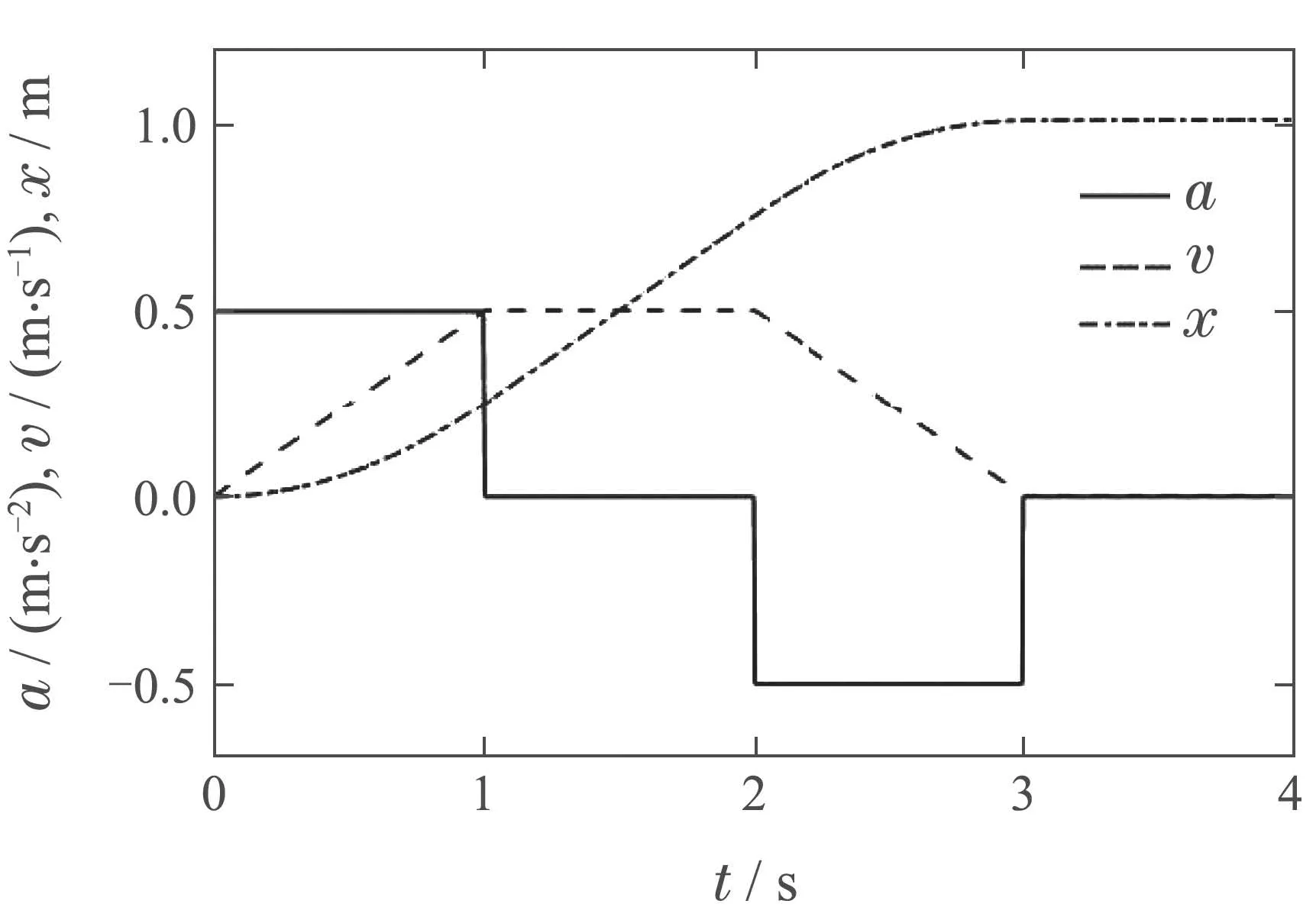
图3 机械臂的加速度a,速度v,位移x曲线Fig.3 The acceleration a,velocity v and displacement x acceleration curves

4.2 自适应输入整形控制

选取某一品种的西红柿作为采摘样本,求取果实的平均质量为m=0.25 kg,果茎平均长度l=0.04 m.首先,采用ZV输入整形算法,取µ=0.07,重力加速度g=9.8 m/s2.根据式(4)–(5)可得

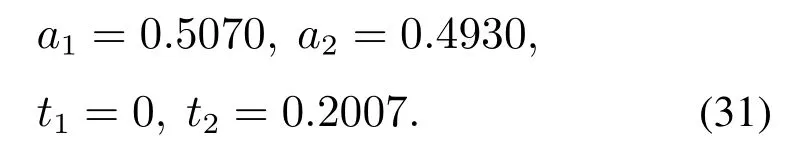
则参考输入r和ZV整形后的输入uzv如图4所示.

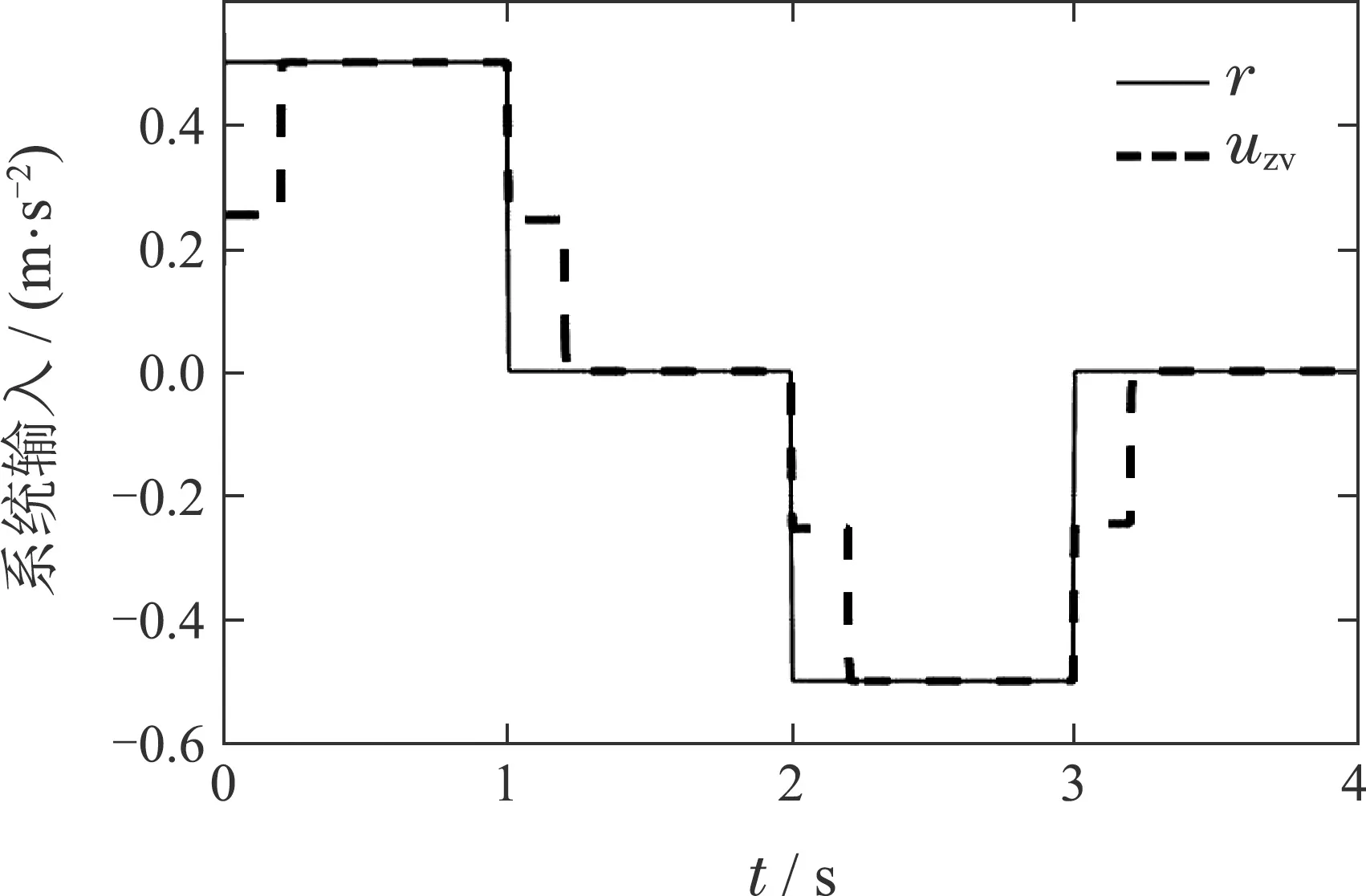
图4 参考输入r和ZV整形后的输入uzv曲线Fig.4 The input signal r and shaping signal uzv curves

在r和uzv的作用下,系统的输出摆角θ和θzv如图5所示.可看出,加入ZV输入整形后,极大的减小柔性负载的摆动.

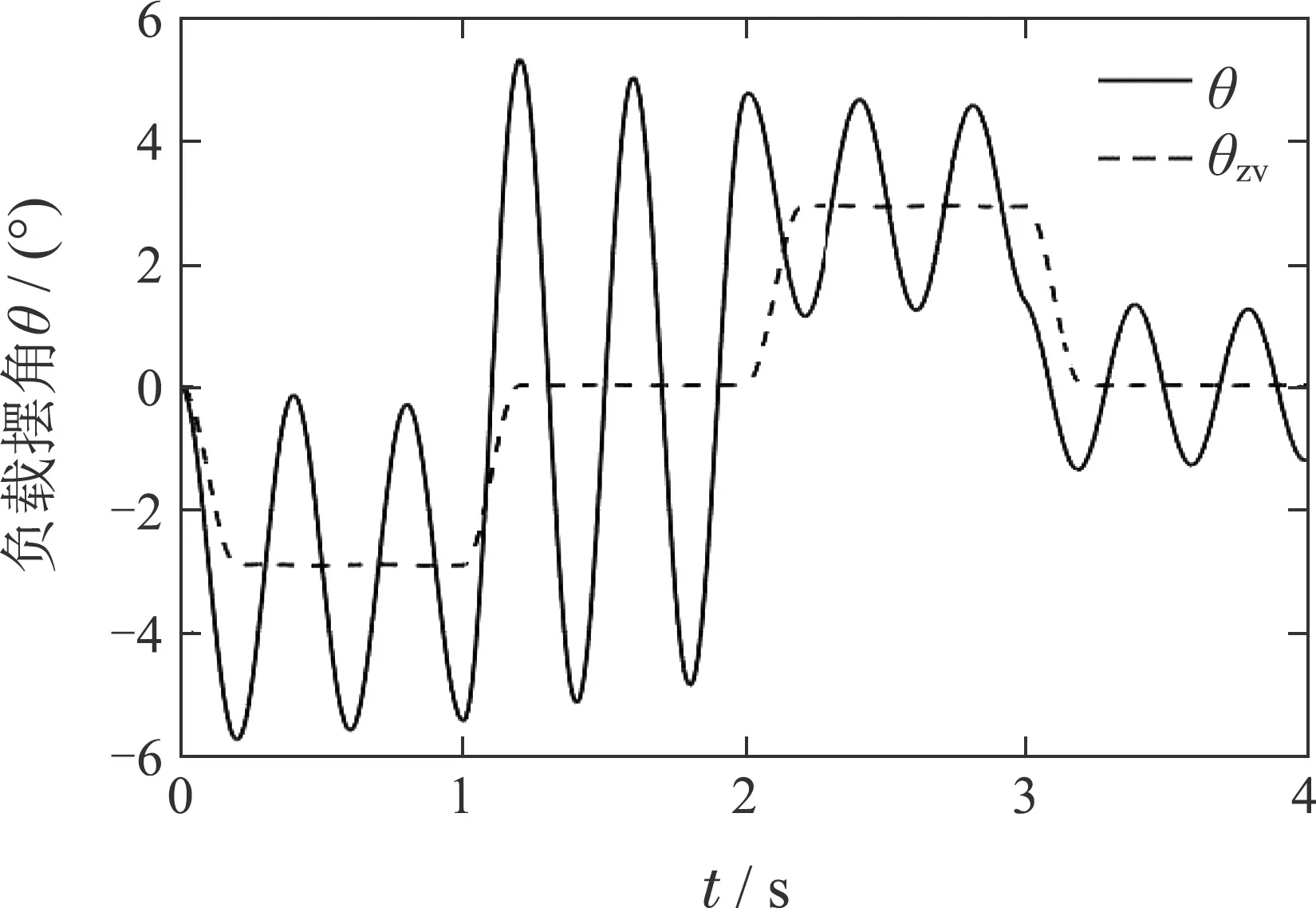
图5 输出摆角θ和θzv曲线Fig.5 The output signal θ and θzv curves

但在实际控制中,果实的质量和果茎长度,也就是负载质量m和柔性连杆长度l都是变化的,导致系统模型也会发生改变.因此在样本果实平均质量和果茎平均长度的基础上,考虑3组负载参数改变的情况(∆m,∆l).

第1组:柔性连杆长度不变,负载质量减小或增加∆m=±0.05 kg:

(−0.05,0),(+0.05,0).

第2组:负载质量不变,柔性连杆长度减小或增加∆l=±0.01 m:

(0,−0.01),(0,+0.01).

第3组:负载质量和柔性连杆长度均发生改变∆m,∆l:

(−0.05,−0.01),(+0.05,−0.01),

(−0.05,+0.01),(+0.05,+0.01).

在3组变负载情况下,采用ZV输入整形控制的输出摆角θ如图6所示.可看出,负载质量和柔性连杆长度发生变化后,会导致ZV整形器不能起到很好的控制效果,负载摆角出现明显震荡.

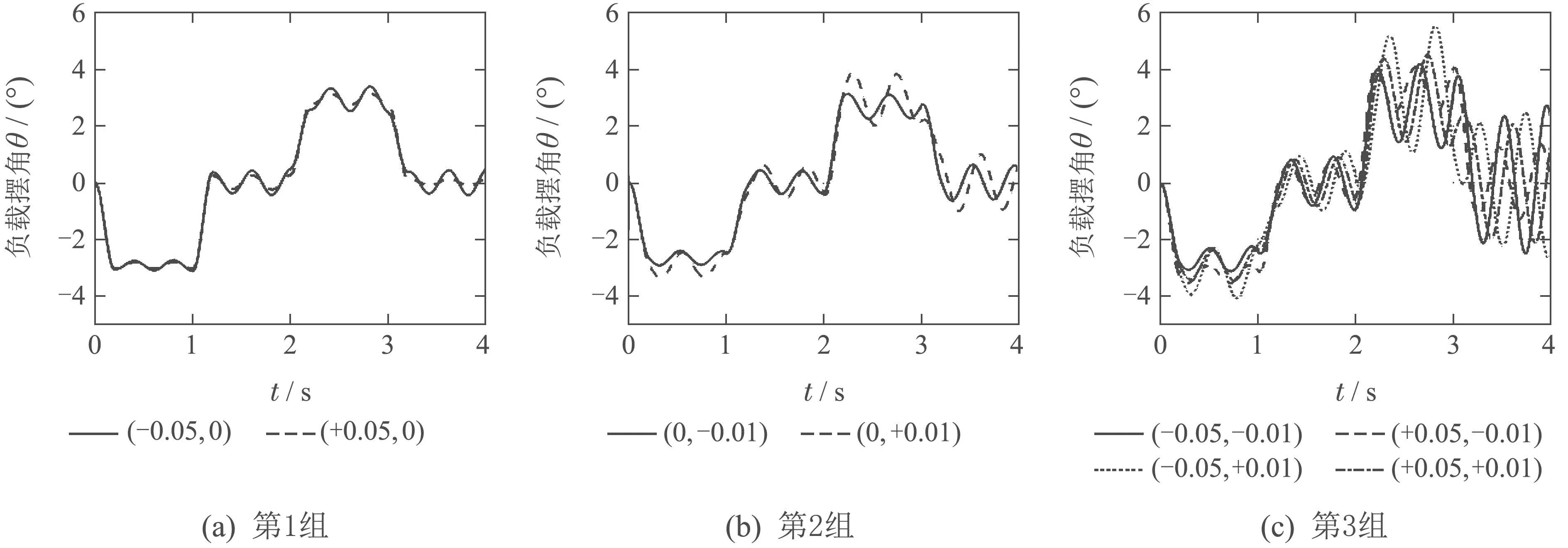
图6 负载参数改变时的输出摆角θ曲线Fig.6 The output signal θ of changing load parameters

因此,采用两个输入脉冲的自适应控制算法,根据整形后的控制量u,和负载的输出摆角θ,在线的调整整形器的参数.设自适应算法K=100,遗忘因子λ=0.999,式(23)–(25)中的初始值为S0=0,T0=0,X0=I,自适应整形器的脉冲幅值和时间初值仍为式(31)中ZV整形器的参数值.

在3组负载变化的情况下,自适应输入整形算法的输入u曲线如图7所示.可看出,自适应算法对输入的脉冲幅值和时间均进行了迭代计算.

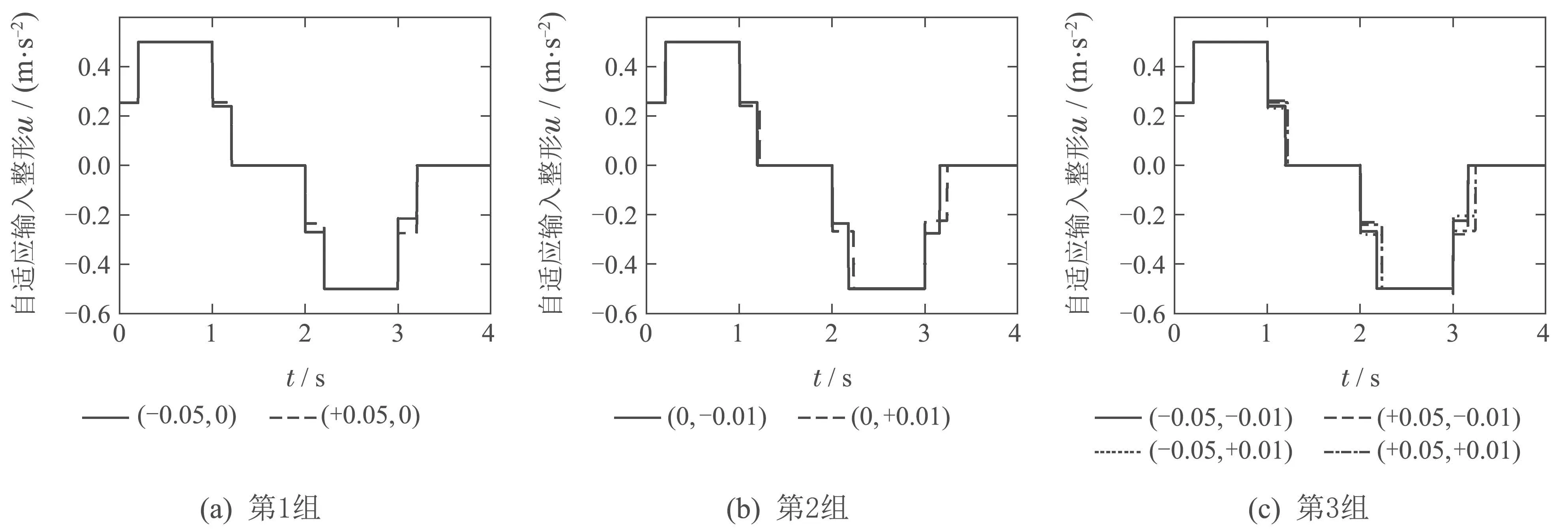
图7 自适应输入整形后的输入u曲线Fig.7 The input signal u curve of adaptive input shaping

在自适应输入u的作用下,3种情况的负载的输出摆角经过加速运行阶段的调整,在进入匀速运行阶段时,摆动幅度大大减小,进入减速运行阶段后,达到了满意的控制效果.3种情况的系统负载输出摆角θ如图8所示.

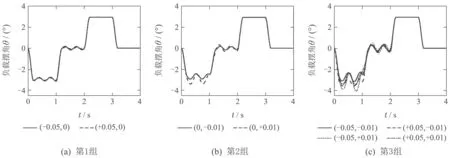
图8 自适应输入整形后的输出θ曲线Fig.8 The input signal θ curve of adaptive input shaping

自适应输入整形算法的脉冲幅值迭代过程如图9和图10所示.基于时间最优约束条件,设第1个脉冲时间t1=0,第2个脉冲时间t2的迭代曲线如图11所示.

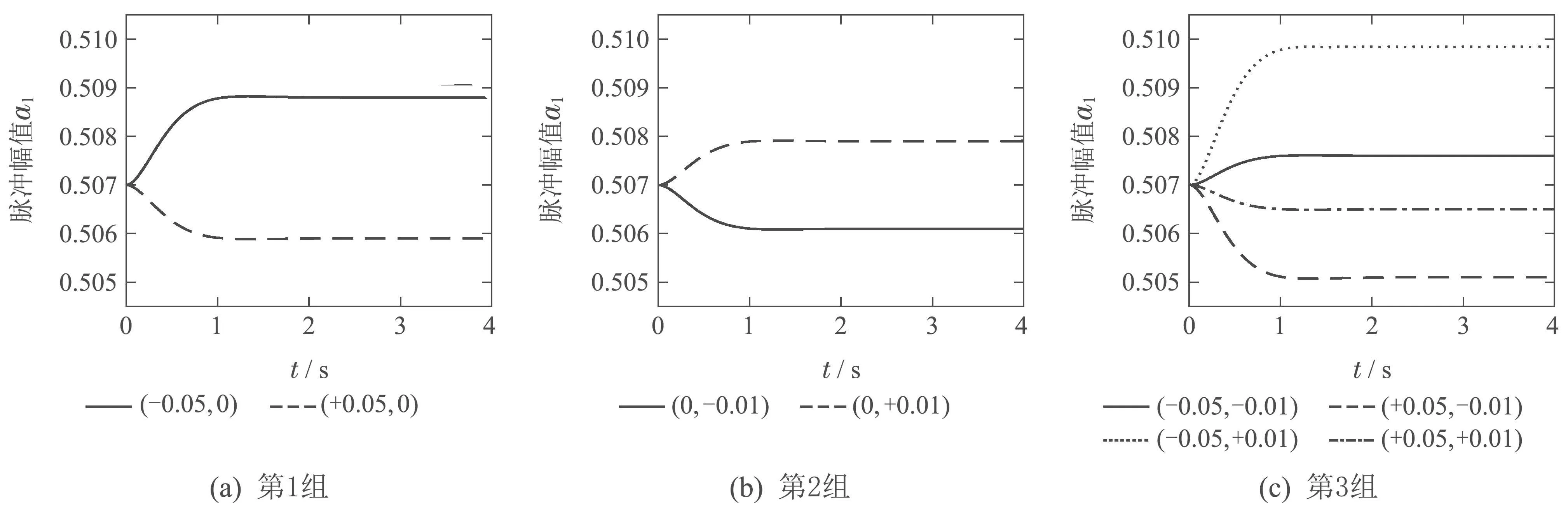
图9 自适应输入整形脉冲幅值a1迭代曲线Fig.9 The amplitude parameters a1 of adaptive input shaping

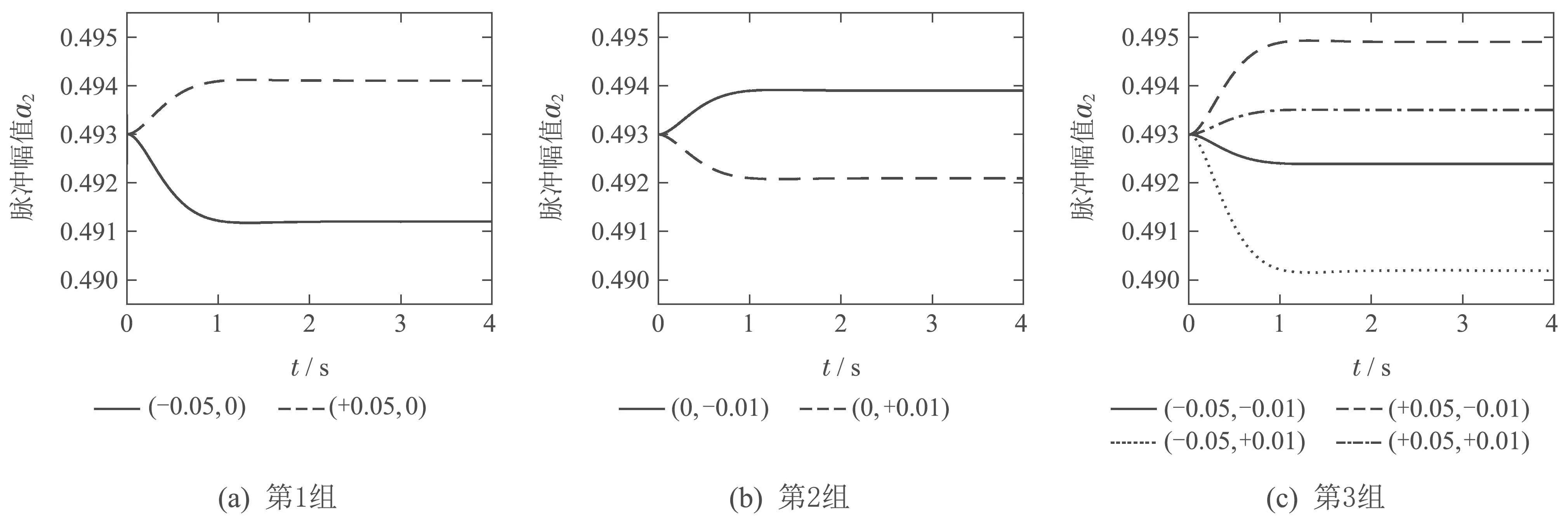
图10 自适应输入整形脉冲幅值a2迭代曲线Fig.10 The time parameters a2 of adaptive input shaping

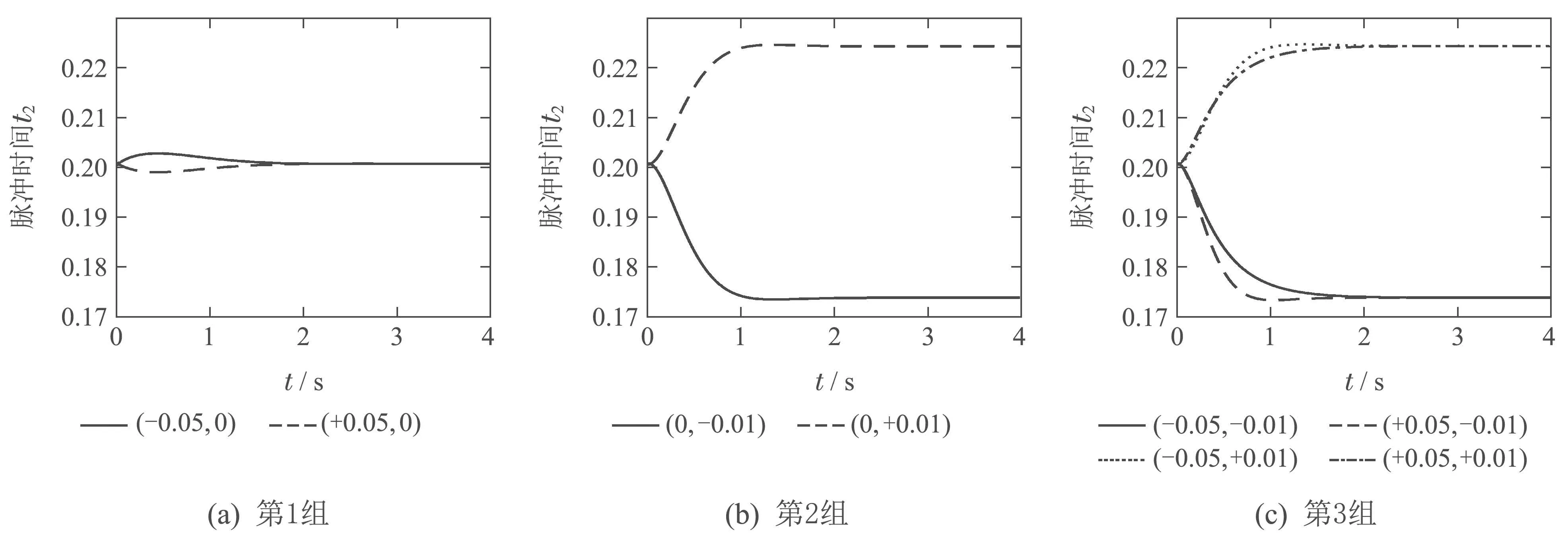
图11 自适应输入整形脉冲时间t2参数迭代曲线Fig.11 The time parameters t2 of adaptive input shaping

5 结论

本文针对机械臂抓取可变柔性负载移动过程中的振动抑制问题,提出了自适应输入整形控制方法.设置二次型性能指标函数,对机械臂移动的加速度和负载的摆角数据进行迭代运算,实时计算整形器的脉冲的幅值和时间,达到减小残余振动的目的.针对负载的质量和柔性连杆长度两个可变参数,考虑柔负载的3种变化情况,实验结果证明了本文所提方法的鲁棒性,获得满意的控制性能.