浅谈函数思想在高考数学中的应用

简蕾郦

(贵州省遵义市第四中学 贵州 遵义 563000)

函数思想就是用变量对应的观点思考问题，紧扣定义，利用图像和性质分析问题、转化问题，进而使问题得以解决。自函数出现之后，数学家们在探索问题、进行科研的时候，就会产生运用函数思维的意识，并在使用中可以让更多问题迎刃而解。据此，数学家总结了这种思维意识的共同点，即变化的量与不变的量之间存有一定关系，并借助变量这一要素解决数学问题，这就是函数思想。在此可以通过发现问题，依据问题的数学特征建立关系式，在此过程中挖掘隐含条件，能够构建数学函数的模型，最后通过解答函数模型，解决问题。

1.近几年高考试卷对函数思想考察的分析

1.1 对函数思想体现形式的分析。经过对近几年高考试卷中函数思想有关问题体现形式的分析，发现关于此类问题的呈现一目了然，有的是直接给出函数性质、图像、等量关系，有的是需要进一步思考才能想到是要运用函数思想解决、有的函数思想则是直接隐藏在题干中。

此问题中的函数思想是通过外显形式呈现的，题干中，直接给出了函数的等量关系、周期、定义域等信息，只需要使用函数思想中的周期性特点，分析分段函数的表达式，列出关于a的方程，然后求解。

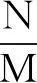
经过对近几年高考试卷中函数思想问题的分析，发现外显形式的问题数量与内隐形式的问题相差不多，如2021年外显与内隐形式的问题数量分别为6道和5道。

1.2 对函数思想考察内容的分析。经过对近五年数学高考试卷进行详细的分析，发现在导数、解三角形、概述概念、平面解析几何、基本初等函数、数列等知识模块中，都有渗透方程思想，其中基本初等函数领域中对于函数思想考察的题目数量最多，还有部分题型是此基本初等函数与其他知识模块中知识的结合。经过对各知识模块中对函数思想的考察，可知高考试卷中在下面几方面中考察学生的函数思想。分别为：基本初等函数问题中函数思想的考察，此考察学生对目标函数的概念、性质与图像的掌握程度，函数中变量关系的分析；不等式的应用中，考察函数思想，需要学生有转换视角，即在不等式中，能够提取等量关系与函数关系，然后借助函数的形式表现出来，让问题更加明朗；数列中函数思想的考察，即借助求解数列的某些性质、通项公式，此也都与函数有一定联系。另外，还可引导学生用函数的眼光看数列，就像一种特殊的函数，其中定义域为正整数集，在此就可利用函数思想解决一些数列问题；导数的应用中函数思想的考察，导数是数学高考试题中的重难点，一般考察的是学生对函数、导数的单调性的认知，是否能借助导数，求解函数的最值与极值问题。此就是在导数问题解答中运用函数思想。

1.3 对函数思想考察要求的总体分析。经过对近几年高考试题中函数思想的考察分析，可以将对学生函数思想的考察，分为下面几个水平：水平一，对于高中阶段接触的几种函数，了解概念、基础性质、图像等知识。可以用函数解决简单的数学问题，初步了解函数思想的价值与作用。水平二，在涉及函数思想的相关问题中，能够提炼出题干中已知量与未知量，知道两者的关系，进一步将复杂的数量关系简单化，能够使用对应的函数性质，解决数学问题[1]。水平三，能够在综合情境中，通过题目的文字信息，挖掘出隐藏的函数知识，如性质、等量关系等，以此扩展函数性质，将数学问题，转换成函数问题，能够构建新的方程，创造性的运用函数思想解决实际问题。

2.函数思想在数学教学中的应用

2.1 在数列教学中渗透函数思想。

2.1.1 在概念教学中渗透函数思想。高中数学课堂中对数列概念本质的教学渗透函数思想，可以助学生加强对数列概念的理解，另外还能巩固函数思想。定义数列时，教材中指出，数列可以看成是以正整数集N+(或它的有限子集{1,2,…,n})为定义域的函数an=f(n)当自变量按照从小到大的顺序依次取值时所对应的一列函数值。只要教师带领学生们想到这一层，就会从函数思想思考数列的概念，会发现数列实际上就是一个离散的函数，进一步加深对数列的记忆。基于此，当学生掌握数列概念的时候，就会对函数思想有更多的认知。

2.1.2 在教授数列相关公式时渗透函数思想。对于高中数列部分的学习，同学们将主要学习两类特殊数列——等差数列和等比数列，这两类数列的定义、通项公式及其推导，前n项和公式及其推导都非常重要，教师在教授此过程知识的时候，引导学生将次与函数思维结合，引导学生从函数的角度探究前n项和与等差、等比数列通项公式，快速构建系统性知识脉络。例如，学生在学习等差数列通项公式的内容时，教师不妨引领学生，从以前学习的函数的角度分析数列，即将通项公式中的n当做自变量x，an做因变量y，所以等差数列的通项公式，就可看做一次函数y=kx+b，只是此处的x的取值范围是正整数值。通过此，教师还可以引导学生掌握d在一次函数中的意义，即当自变量的数增加1，函数值的变化量为k。在此，还可以将公差d当做等差数列的斜率、导数与变化率。然后教师带领学生画出一次函数与等差数列的图像，进一步知道等差数列的图像，实际上就是在一条必经点(1，a1)、斜率为d的直线上的，孤立的点。自此，若已知等差数列的首项和公差，就能结合直线的斜率方程，得到通项公式。如果知道等差出列的两项，那么也结合直线的两点方程，得到通项公式。

2.1.3 在例题讲解中渗透函数思想。数列课堂例题讲解环节中渗透函数思想是必要的，学生经常会模仿教师们分析问题的过程，包括使用什么方法解题、书写解题的步骤等。在此，教师在开展例题讲解的时候，如果还使用传统的常规讲解法，不深入挖掘函数思想。那么学生在模仿下也不会深入思考，有时不能找到更简单的方法解答问题。此与新课标提出的“重视数学思想的教学”理念是违背的，会让学生在一定程度上，也忽视方程思想的运用。基于此，在例题的讲解中，教师不只要知道怎么进解，还要知道怎样讲才能揭示函数思想，加强对问题解答过程中，方法与思想的概括，让学生能够深刻的、更好的内化函数思想。对于函数一章的例题讲解，教师要先肯定学生的解题方法，然后深入引导，让学生尝试从函数的角度，再思考问题，使用函数思想解答问题。最后，将常规解答与使用函数思想解答问题的方法做比较，让学生通过类比的方法，知道使用函数思想解题的好处，进而在后期做相关习题的时候，能够尝试使用函数思想解答，快速解答问题。

2.2 初等函数教学中函数思想的渗透。学生刚步入高中的时候就会接触基本初等函数，而高考试卷中关于基本初等函数的试题，经过千变万化，更具深度与广度[2]。如细胞分裂、人口增长等相关问题涉及指数型函数；溶液中PH值变化、地震时的地震级的破洞类问题涉及对数型函数；正方体的边长和正方体体积的关系、气体压强与体积的关系等问题，涉及的是幂函数。由此可知基本函数的学习对学生们将来解决实际问题有重要意义。以对数与对数运算的教学为例，本节课的教学要建立在指数的教学上进行，因为是完全陌生的知识结构，所以更容易引入函数思想开展教学。近几年的高考试卷中，数与对数的运算的习题也占有不小的比例，需要教师生重视，创建高效课堂。教学过程：情境导入，教师首先使用多媒体向学生展示细胞分裂的过程，紧接着提出疑问，请问经过五次分裂后一个细胞变成了多少个呢？继续追问，细胞个数达到512个需经过几次分裂呢？分裂次数如何表示你有什么好的想法吗？在学生们完成问题的回答后，可以为对数概念进行定义，即ax=N(a>0，a≠1)，此时x就是以a为底，N的对数。在此，a就是底数，N是真数。然后教师对对数概念进行详细的说明，如33=27就是以3为底，27的对数为3，在此将ax=N与33=27放在一起研究，就知道了指数与对数之间的关系。另外，如果一个对数的底数为10，此就是常用对数，直接基座log10N。在此要记住，并不是所有的指数都能转化为对数式，只有a在大于零，不等于1的时候才可以。在学生们掌握对数式和指数式异同之后，就可做课后习题，在做题过程中，尝试完成指数与对数式的互换，从指数的意义分析对数。

2.3 在不等式解题中渗透函数思想。利用函数思想解决高中数学中的不等式问题时，常常需借助函数图像和整体换元等方法。

首先，函数的图像一直是历年来中考试卷中高频出现的，在不等式问题的解答中使用函数图像，可以让问题变得更加直接与形象，即使是复杂的不等式问题，通过位置的呈现，会让学生的观察更具直观性，将抽象的问题具体化。在此教师要教授学生掌握函数图像的一般变化规律，可以从实际角度入手，简化不等式问题的解题步骤。下面借助对应的不等式问题的讲解，助学生更好的把握解题思维与过程。

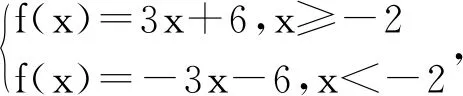
分析，对于此问题的解答，可以通过作图的形式，即做出y=2x-m和y=f(x)的图像。分析题干中的条件，因为不等式f(x)≥2x-m恒成立，那么画出函数y=2x-m的图像，会发现其一直在y=f(x)的下侧[3]。因此，当x=-2时，y=-m-4则小于等于0，可以得到m大于等于-4，由此可以得到实数m的取值范围为[-4，+∞)

经过本问题的分析，可知高中数学中不等式问题的解答多是和函数图像结合的，可以结合不等式问题，绘制一个或者两个对应的函数，在直角坐标系中根据图像的位置关系，直接确定参数范围。总的来说，借助数形结合的方法解决不等式问题，核心就构造函数，只要学生们感悟这一点，就可快速的解答不等式问题。

其次，函数思想是2022高考试卷解答中常用的思想，也是学生们解题时使用最频繁的思维。在解答不等式问题的时候，函数思想的运用下，可以转化题干中给出的信息，以此快速分析问题，解决问题，从不等式中数量关系着手，建立成熟的数学模型，然后解答。

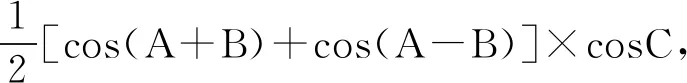
最后，对于不等式中最值问题的研究，注重对式子的等价变形，高中阶段的学生要在数量掌握基本初等函数的概念、性质、图像基础上，将不等式中的复杂的、不常见的函数转化为基本函数，通过此为解题提供便捷[4]。在此，最常见的不等式形式是F(x)=f(x)-g(x)，大于或者小于零恒成立的题型，此也可以等价转化为[f(x)]min>(或者<)[g(x)]min的最值问题。在解答此类问题的时候，要明确哪一个是自变量，哪一个是参数，这两个量在特定情况系还可以互相转化，所以在实际解答中，经常是最值问题与恒成立的问题结合的形式呈现。

结论

函数是高中数学学习的主线，是高中数学最重要的内容之一，学生学好函数，掌握函数思想，对他学好高中数学将产生巨大的促进作用。学生们在初中阶段，虽然接触过函数思想，但是到了高中，接触的函数知识更多与更复杂，遇到相关问题不知如何用函数思想解答问题，就产生了畏惧感。通过本文对函数思想在高中数学教学中的运用，让学生的解题有数学思想做支撑，将数学学习变得更有趣与丰富多彩。