过球心的平面与球面相交所得空间圆周的参数方程

张 辉, 李应岐，方晓峰，王 静

(火箭军工程大学 基础部，陕西 西安 710025)

0 引言

在空间曲线学习中，常常会遇到一个特殊的空间圆周Γ，它是由球心为M(x0,y0,z0)、半径为a(a>0)的空间球面与过球心M的平面A(x-x0)+B(y-y0)+C(z-z0)=0(A、B、C不全为零)相交所得，则此空间圆周Γ的一般方程为

在某些实际问题中，需要利用空间圆周Γ的参数方程方便求解，那么如何得到空间圆周Γ的参数方程呢？

1 空间圆周的参数方程

空间圆周Γ作为一类特殊的空间曲线[1-3]，为了求出Γ的参数方程，下面分3种情形进行分析讨论。

情形1系数A、B、C中一个不为零而其他两个均为零。

不妨假设A≠0、B=0、C=0，则过球心M的平面方程为x-x0=0，将其代入球面方程(x-x0)2+(y-y0)2+(z-z0)2=a2中得(y-y0)2+(z-z0)2=a2。记y=y0+acost、z=z0+asint，故空间圆周Γ的参数方程为

式中，0≤t<2π。对于A=0、B≠0、C=0和A=0、B=0、C≠0的两种情形同理可得。

情形2系数A、B、C中两个不为零而其他一个为零。

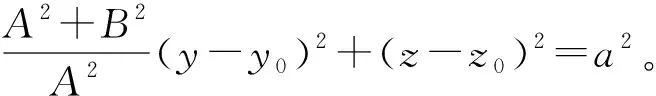
式中，0≤t<2π。对于A=0、B≠0、C≠0和A≠0、B=0、C≠0的两种情形同理可得。

情形3系数A、B、C全不为零。

为方便求解，作平移变换

即得到一个新的空间圆周Γ′，

下面先求解空间圆周Γ′的参数方程，进而得到空间圆周Γ的参数方程。因为(A,B,C)和(-A,-B,-C)都可以作为空间平面AX+BY+CZ=0的法向量，为研究方便起见，不妨假设C>0。

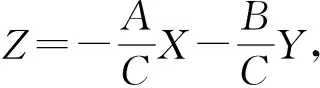
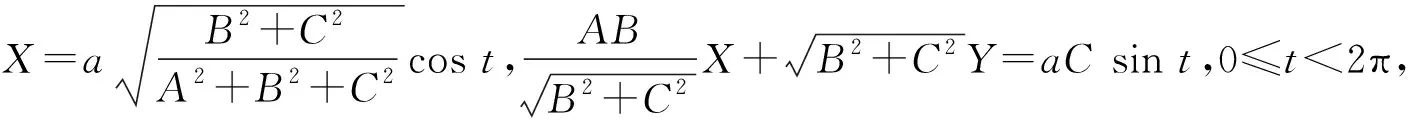
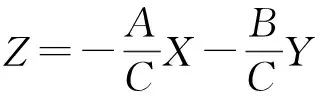
故空间圆周Γ的参数方程为

(1)

其中，0≤t<2π ，对于系数A、B、C全不为零时空间圆周Γ的参数方程的求解问题，还可以利用球面的参数方程解决。

由球面坐标变换，记

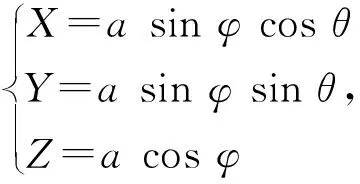
0≤φ≤π，0≤θ<2π，代入方程AX+BY+CZ=0中得

Asinφcosθ+Bsinφsinθ+Ccosφ=0，

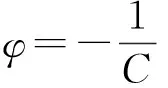
此时便有

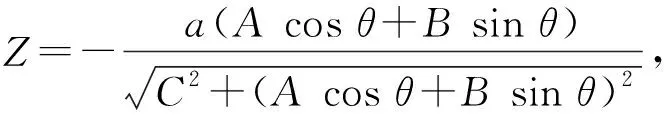
其中，0≤θ<2π。

以上是从两个不同角度分析得到空间圆周Γ的参数方程。此时需要关注的一个问题是，方法一中的参数t与方法二中的参数θ是否有内在的联系呢？为了研究此问题，从此空间圆周上一些特殊的点出发来寻找答案。令t=0，对应空间圆周Γ上的点记为A，其坐标为

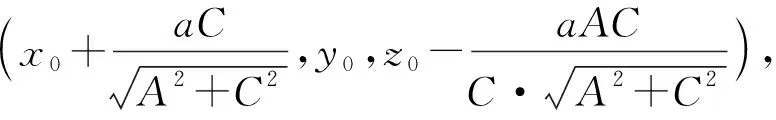
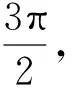
且处在空间直角坐标系第Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ、Ⅷ卦限内。利用MATLAB可以描绘出此空间圆周Γ以及其上的关键点，如图1所示。

图1 球面x2+y2+z2=1与平面x+y+z=0相交所得的空间曲线Fig.1 Intersection curve of the sphere x2+y2+z2=1 and plane x+y+z=0

值得注意的是，空间圆周

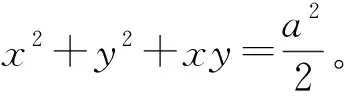
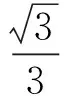
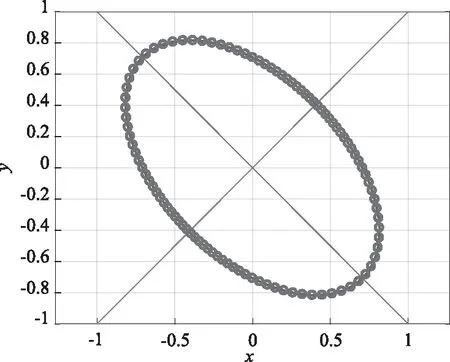
图2 空间曲线在xOy坐标面上的投影曲线Fig.2 Projective curve in xOy coordinate surface

2 两个应用

对于情形3，利用所得的空间圆周Γ的参数方程(1)，通过计算可得

进而

若将参数方程(1)看成空间某质点运动轨迹的参数方程，则该质点是作匀速率为a、匀加速率为a的空间圆周运动。借助于图1，可以看成该质点从起始点(位置A)经时间π/2运动到位置点D,再经时间π/2运动到位置点E,又经时间π/2运动到位置点G,最后经时间π/2运动到起始点(位置A)，且从z轴正向来看按逆时针方向运动。也就是说，参数方程(1)中的参数t可以看成质点运动的运动时间。

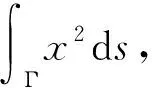
其中，a>0，A、B、C全不为零。对于此问题，参数方程(1)中的参数t的取值范围[0,2π]，利用化第一类曲线积分为定积分的方法可得

需注意的是，如果积分曲线Γ不是封闭空间圆周，但只要知道参数方程(1)中参数t的取值范围，便可确定定积分的上限和下限进而利用微积分基本公式来求解。

3 结语

本文研究了过球心的平面与球面相交所得空间圆周的参数方程问题，根据系数的取值特点分3种情形进行了分析讨论，并介绍了参数方程的物理意义以及在第一类曲线积分计算中的应用。