交错二项式系数连带奇数倒数平方和级数
张来萍, 及万会
(1.宁夏大学 新华学院,宁夏 银川 750021;2.宁夏民族职业技术学院 教育系,宁夏 吴忠 751100)
0 引言
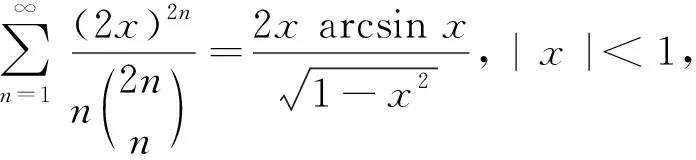
1 主要结果和证明
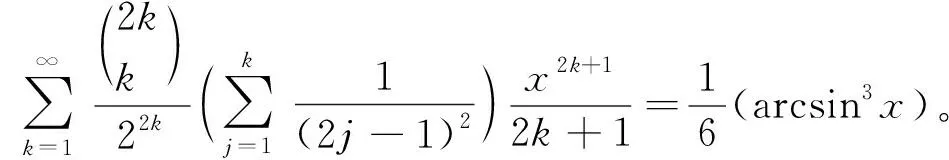
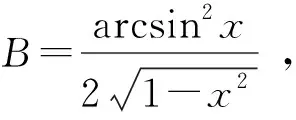
(1) 奇数倒数平方和级数的二项式系数分母包含1个因子:
(1)
(2)
(3)
(4)
(5)
(2)奇数倒数平方和级数的二项式系数分母包含2个因子:
(6)
(7)
(8)
(9)
(10)
(11)
(3)奇数倒数平方和级数的二项式系数分母包含3个因子:
(12)
(13)
(14)
(15)
(4)奇数倒数平方和级数的二项式系数分母包含4个因子:
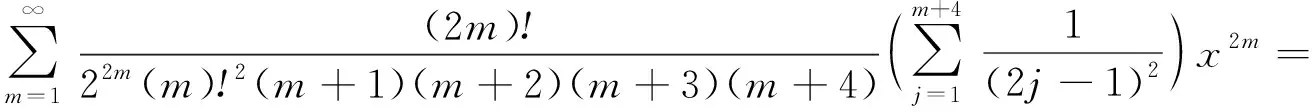
(16)
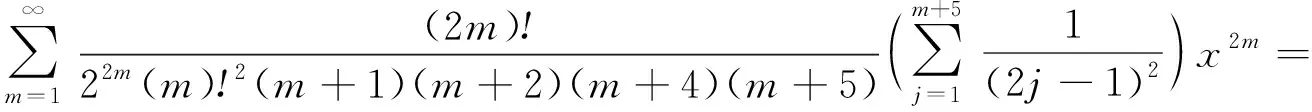
(17)
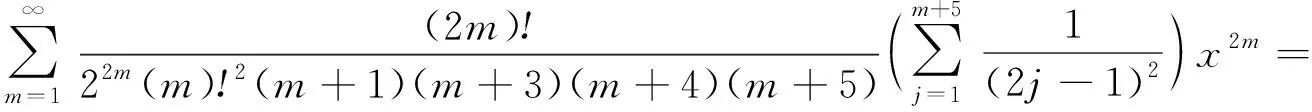
(18)
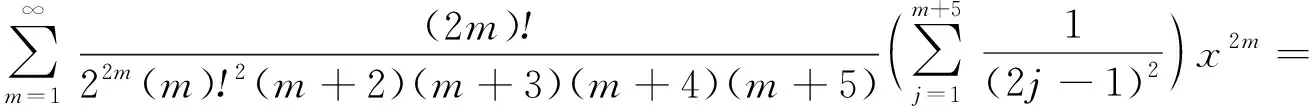
(19)
(5) 奇数倒数平方和级数的二项式系数分母包含5个因子:
(20)
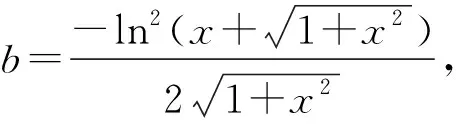
(1) 奇数倒数平方和级数的二项式系数分母包含1个因子:
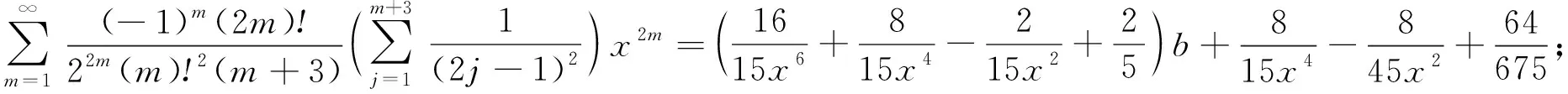
(2)连续奇数倒数平方和级数交错的二项式系数分母含有2个因子:
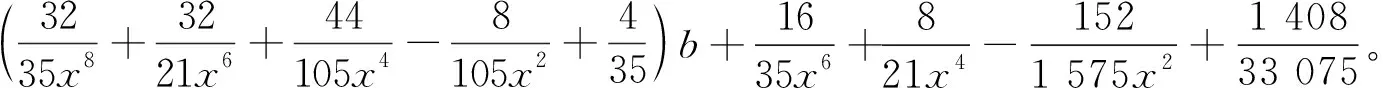
(3)连续奇数倒数平方和级数交错的二项式系数分母含有3个因子:
(4)连续奇数倒数平方和级数交错的二项式系数分母含有4个因子:
(5)交错的二项式系数连带连续奇数倒数平方和级数的分母含有5个因子:
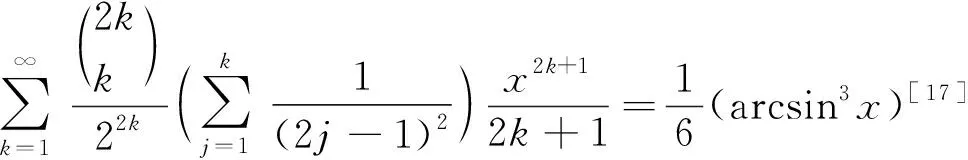
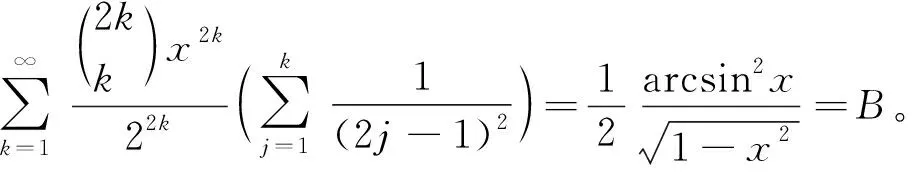
(21)
(1)对(21)式左边进行裂项:
设k-1=m,则有
化简得
B1即为(1)式。
(2)对(21)式左边继续进行裂项:
设k-2=m,则有
(22)
(22)式左边转化成部分分式,则有
因为B,B1已知,故通过计算可有
B2即为(2)式。
(22)式中B,B1,B2都已知,便可得2个因子乘积的二项式系数连带连续奇数倒数平方和级数公式(6)。
(3)对(21)式的左边进行裂项运算:
令k-2=m,则有
(23)
将(23)式的每个分式化成部分分式,则有
其中B,B1,B2都已知,通过计算得
B3即为(3)式。
分别设
以B3证明连续奇数倒数平方和上标增加1项或几项不改变其和式收敛性。
前和式为二项式系数连带连续奇数倒数平方和表达式,后式极限趋于0。
则有
结论:连续奇数倒数平方和上标增加1项或几项不改变其和式收敛性。
(23)式中留下2个因子的分式,其他转化成部分分式,对这些2个因子的分式,每次保留1个,其余化成部分分式,则有
其中B,B1,B2,B3已知,通过计算可得(7)~(8)式。
(23)式中留下3个因子分式,其余的分式转化成部分分式,则有
其中B,B1,B2,B3已知,通过计算可得(12)式。
(21)式左边进行裂项运算:
令k-4=m,则有
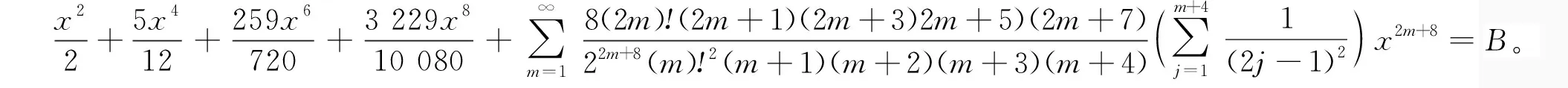
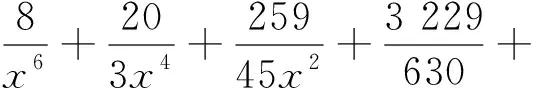
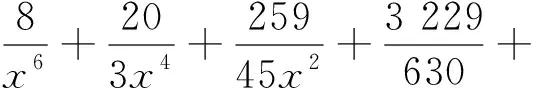
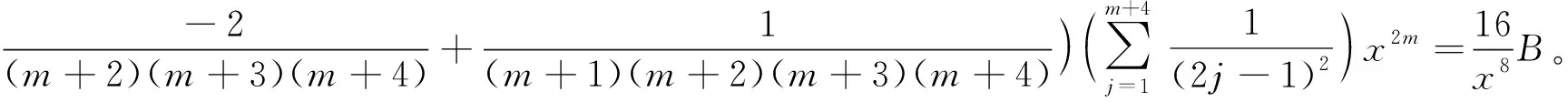
(24)
将(24)式的分式化成部分分式,则有
此时B,B1,B2,B3已知,通过计算可得
B4即为(4)式。
在(24)式中留下有2个因子的分式,其余化成部分分式,则有
此时B,B1,B2,B3,B4已知,通过运算可得(9)~(11)式。
(24)式中留下3个因子的分式其余化成部分分式,可得
此时B,B1,B2,B3,B4,B5已知,通过运算可得(13)~(15)式。
(24)式中保留4个因子的分式,其余化成部分分式,可得
此时B,B1,B2,B3,B4已知,通过运算可得(16)式。
(21)式的左边进行裂项运算:
设k-5=m,得
展开乘积表达式,得
(25)
在(25)式中含有1个因子分式、2个因子分式、3个因子分式、4个因子分式、5个因子分式。本文仅选1个因子分式、4个因子分式、5个因子分式,将分式化成分母为1个因子、4个因子、5个因子乘积的二项式系数连带连续奇数倒数平方和级数。
(25)式中所有分式化成部分分式,可得
此时B,B1,B2,B3,B4已知,通过运算可得
B5即为(5)式。
在(25)式保留4个因子分式,然后对这些4个因子的分式,每次保留1个,其余化成部分分式,可得
此时B,B1,B2,B3,B4,B5已知,通过运算可得(17)~(19)式。
(25)式中留下5个因子分式,其余化成部分分式,可得
此时B,B1,B2,B3,B4,B5已知,通过运算可得(20)式。定理证毕。
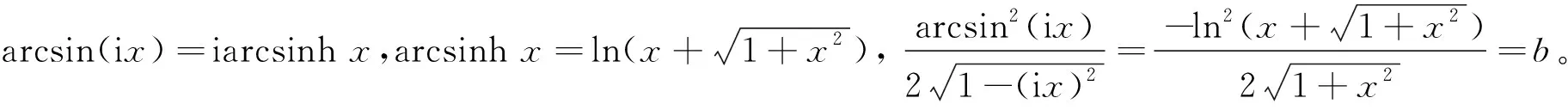
2 数值级数恒等式
推论1分母为奇偶性不定因子乘积的二项式系数连带连续奇数倒数平方和数值级数恒等式。
推论2分母为奇偶性不定因子乘积交错的二项式系数连带连续奇数倒数平方和数值级数。

