区域转换下郑州天气衍生品定价研究

0 引言

天气衍生品是一种金融衍生工具,它的交易对象为各种天气指数(如温度、湿度、降雨量、风力等),用来防范或规避非灾害性天气风险,减少极端天气对经济带来的损害。天气衍生品最早于1997年出现在美国,是对冲各种不同气候风险的最重要和最受欢迎的金融工具。天气衍生品在我国属于新型衍生品,其探索还处于初级阶段,国内市场没有可供交易的天气衍生品,也没有相应的衍生品交易市场。HAMILTON J D[1]引入了一种用于股票价格动态特征的区域转换模型,并验证了两区域模型可以很好地拟合每月股票的市场收益。HAMILTON J D[2]在1989年论文的基础上,对离散的时间序列进行分析,并介绍了EM (expectation-maximization)算法,用于得到离散自回归参数的最大似然估计。ELIAS R S等[3]等则首次讨论了气温的区域转换模型的基本原理,并研究了用区域转换方法建立加拿大多伦多市的温度动力学模型。严佳慧[4]选取了两个经典的温度模型,基于中国5个典型城市的温度数据对天气衍生品进行了定价,并分析比较了两种模型的差异。

本文主要探讨基于郑州市日平均气温的定价问题,从实证角度探讨适用于描述郑州市气温数据的模型,更准确地为天气衍生品定价,从而能够应用天气衍生品市场有效管理天气风险。

1 数据与模型建立

1.1 数据来源与描述

气温是天气衍生品交易中使用最广泛的天气指数,关于气温常见的指数有取暖指数HDD(heating degree day)和制冷指数CDD(cooling degree day)。本文的气温数据来源于中国天气网,选取2016年7月1日至2020年6月30日河南省最具有代表性的气象站点——郑州气象站的每日最高温度和最低温度。为方便计算,去除闰年2月29日的温度数据,每年的数据按365 d计算,样本数量为1 460个,即时间t=1,2,…,1 460。

定义1日平均温度

其中T(t)max与T(t)min分别为日最高气温与日最低气温。

定义2第1天到第N天的累计取暖指数

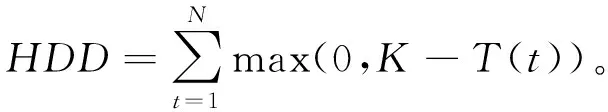
(1)

定义3第1天到第N天的累计制冷指数

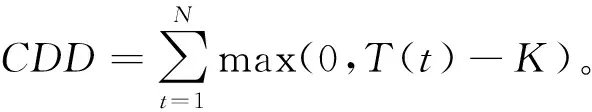
(2)

其中,K是基准温度,取K=18 ℃或65 °F。

利用MATLAB R2020b软件对1 460项气温数据进行统计分析(表1)。为了能够更加准确地描述温度动态过程,考察郑州市的日平均气温残差[5]。

表1 郑州市日平均气温的描述性统计数据Tab.1 Descriptive statistics of daily average temperature in Zhengzhou

在t时刻,假设日平均气温的变化过程可以表示为

yt=T(t)-S(t)，

(3)

其中，周期性和趋势性的函数S(t)可描述为

(4)

为了对气温过程进行模拟,用非线性最小二乘法对式(4)进行拟合获得参数,如表2所示。

表2 周期性和趋势性的函数S(t)的参数拟合值Tab.2 Parameter fit values for the periodic and trending function S(t)

1.2 气温残差模型建立

马尔可夫区域转换模型是一个通过隐变量控制的、在多个随机过程中随机转换的马尔可夫过程。假定存在2个区域变化,则马尔可夫过程转移概率矩阵为

其中,转移概率pij具有性质

对日平均气温残差yt建立以下3种不同的两区域转换模型和1种单个均值回复模型,并检验这些模型对真实数据的拟合效果。

模型1一个均值回复和一个布朗运动模型，

其中，yt,1和yt,2分别表示在区域1和区域2的每日平均气温残差,β1∈R且表示均值回复速度,μ1和μ2分别表示均值回复和布朗运动的均值,σ1和σ2分别表示均值回复和布朗运动的波动率,Wt是维纳过程。

模型2两个均值回复模型，

其中，β1，β2∈R分别表示区域1和区域2的均值回复速度,μ1和μ2分别表示均值回复区域1和区域2的均值,σ1和σ2分别表示均值回复区域1和区域2的波动率,Wt是维纳过程。

模型3两个布朗运动模型，

其中，μ1和μ2分别表示布朗运动区域1和区域2的均值,σ1和σ2分别表示布朗运动区域1和区域2的波动率,Wt是维纳过程。

模型4单区域均值回复模型，

dyt=β(μ-yt)dt+σdWt。

(5)

其中，β∈R表示均值回复的速度,μ表示均值回复的均值,σ表示均值回复的波动率,Wt是维纳过程。

2 研究方法和实证分析

2.1 马尔可夫区域转换模型参数估计

本文主要研究具有两个区域的马尔可夫区域转换模型。由于事先不知道观测数据位于哪个区域,不能直接利用传统的极大似然方法估计参数,采用EM算法对高斯混合模型的参数进行估计[6]。

对于模型1,离散化得到

其中，εt,1和εt,2分别为区域1和区域2独立同分布的标准正态分布。

假设yt,t=1,2,…,N为独立同分布的观测数据,其联合分布为f(yt;θ),θ={θ1,θ2},θ1={β1,μ1,σ1,π1,p11},θ2={μ2,σ2,π2,p22},φ(yt;θ1)和φ(yt;θ2)是高斯概率密度函数,π1,π2≥0分别为yt在时刻t位于区域1和区域2的概率,π1+π2=1,则

f(yt;θ)=π1φ(yt;θ1)+π2φ(yt;θ2)。

区域转换模型中,观测数据yt位于哪个区域是不可见的。以隐变量zt,k表示数据所处的区域,有

其中，t=1,2,…,N;k=1,2,zt,k是0-1型随机变量。

得到完全数据集(y1,y2,…,yN;z11,x21,z31,…,zN1;z12,z22,…,zN2),以及似然函数

(E步)在已知观测数据yt和第t次迭代参数θt下,对完全数据的似然函数取对数,然后再取期望,得到

(6)

求隐变量zt,k的期望,然后再利用贝叶斯公式可得

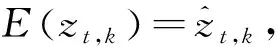
(M步)求Q函数对θ的极大值,也就是求第t+1次迭代参数值

EM 算法重复上述E步和M步过程,直到参数收敛为止。

对于模型2以及模型3,应用EM算法估计参数表达式的过程与上述类似，不再详述。

根据上述推导出的参数表达式,使用MATLAB软件编写EM算法参数估计的迭代计算程序并运行得出如表3所示的参数值结果。

表3 马尔可夫区域转换模型的参数估计结果Tab.3 Parameter values for the Markov regime-switching models

2.2 单区域均值回复模型参数估计

对于单区域均值回复模型,为了估计参数β,μ,σ,离散化式(5)得到

yt=βμ+(1-β)yt-1+σεt，

运用最小二乘法估计出参数结果为β=0.335 8,μ=-0.000 9,σ=2.335 8。

2.3 模型对比

对均值回复过程和布朗运动过程分别利用伊藤引理, 推导出各自区域的显式解为

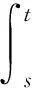
(7)

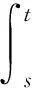
(8)

结合(3)式和(7)式、(8)式, 得到模型1的日平均气温T(t)的解为

采用蒙特卡罗模拟方法,基于4个模型对郑州市2020年7月1日至2021年6月30日的日平均气温进行预测。蒙特卡罗模拟方法模拟100 000次后与真实气温进行对比分析,如图1所示。

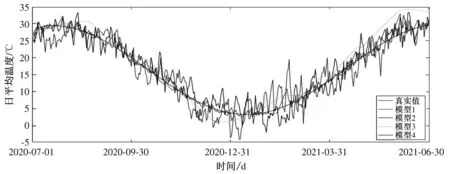
图1 模型拟合值比较Fig.1 Comparison of model fitting values

从图1中并不能明显看出哪一个模型最优,因此需要量化比较不同模型的拟合效果。使用MAE(Mean Absolute Error,平均绝对误差)、MSE(Mean Square Error,均方误差)、RMSE(Root Mean Squared Error,均方根误差)、RAE(Relative Absolute Error，相对绝对值误差)指标进行误差分析,

得到如表4所示的误差分析结果。

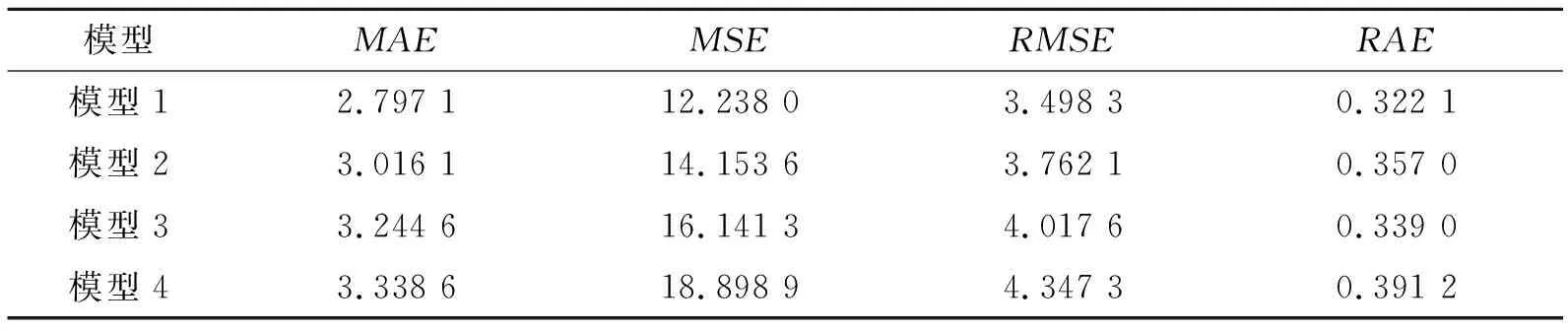
表4 不同模型的误差分析结果Tab.4 Error analysis results of different models

由表4的误差分析计算结果可以看出,模型1的误差小于其他所有模型的误差。也就是说,和其他模型相比，模型1预测的日平均气温更接近真实的日平均气温数据,模型1的气温模型预测效果最好。

3 天气衍生品定价

对比不同基准温度下期限为3,6,9,12个月的真实和模型1预测累计指数值,并计算相对误差率。在假定气温的风险市场价格为0的前提下对气温衍生品定价,此时气温的物理过程恰好是风险中性世界中的价格过程。相对误差率定义为

(9)

使用模型1预测2020年7月1日至2021年6月30日的日平均气温值,并根据式(1)和(2)编写MATLAB程序计算各个月份不同基准温度下的真实和预测累计指数值(结果见表5和表6),并进行气温期权定价。

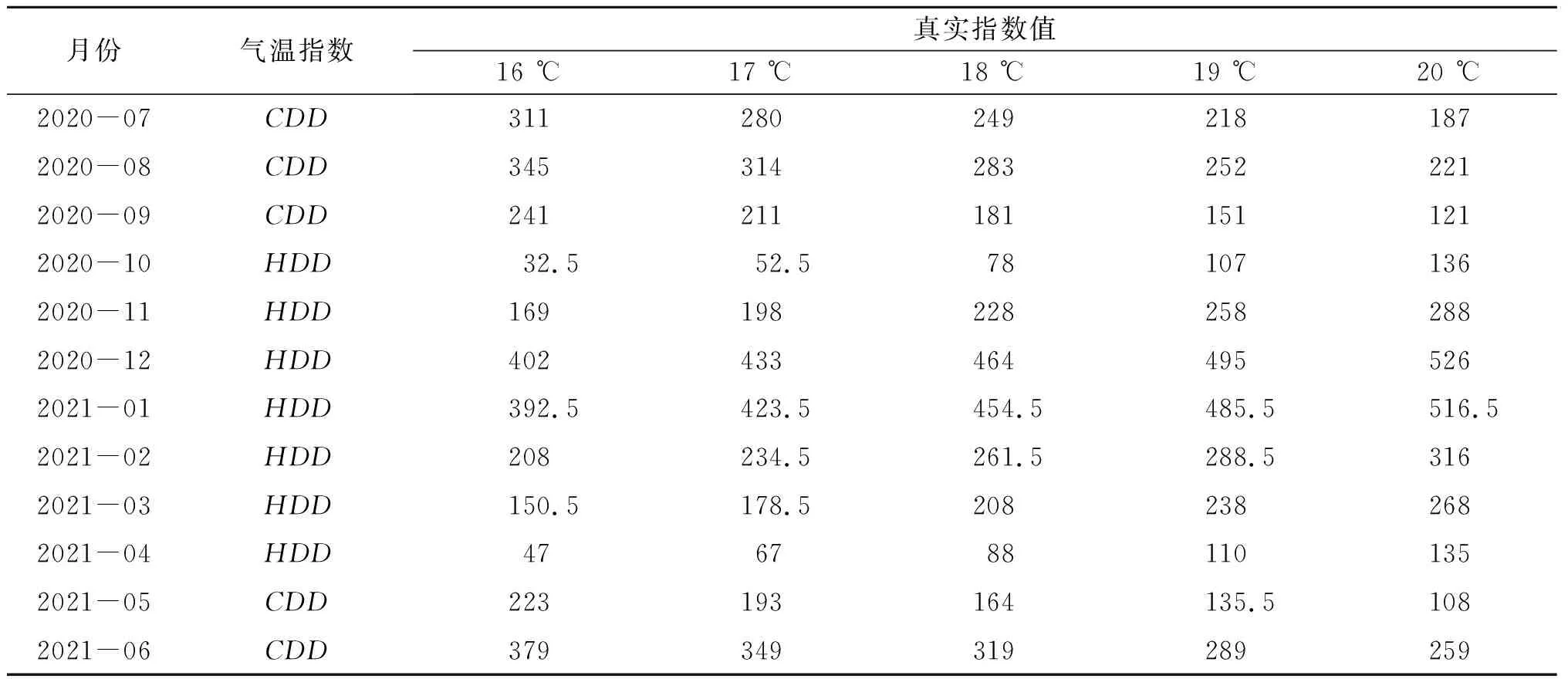
表5 不同基准温度下的真实指数值Tab.5 Actual index value at different baseline temperatures

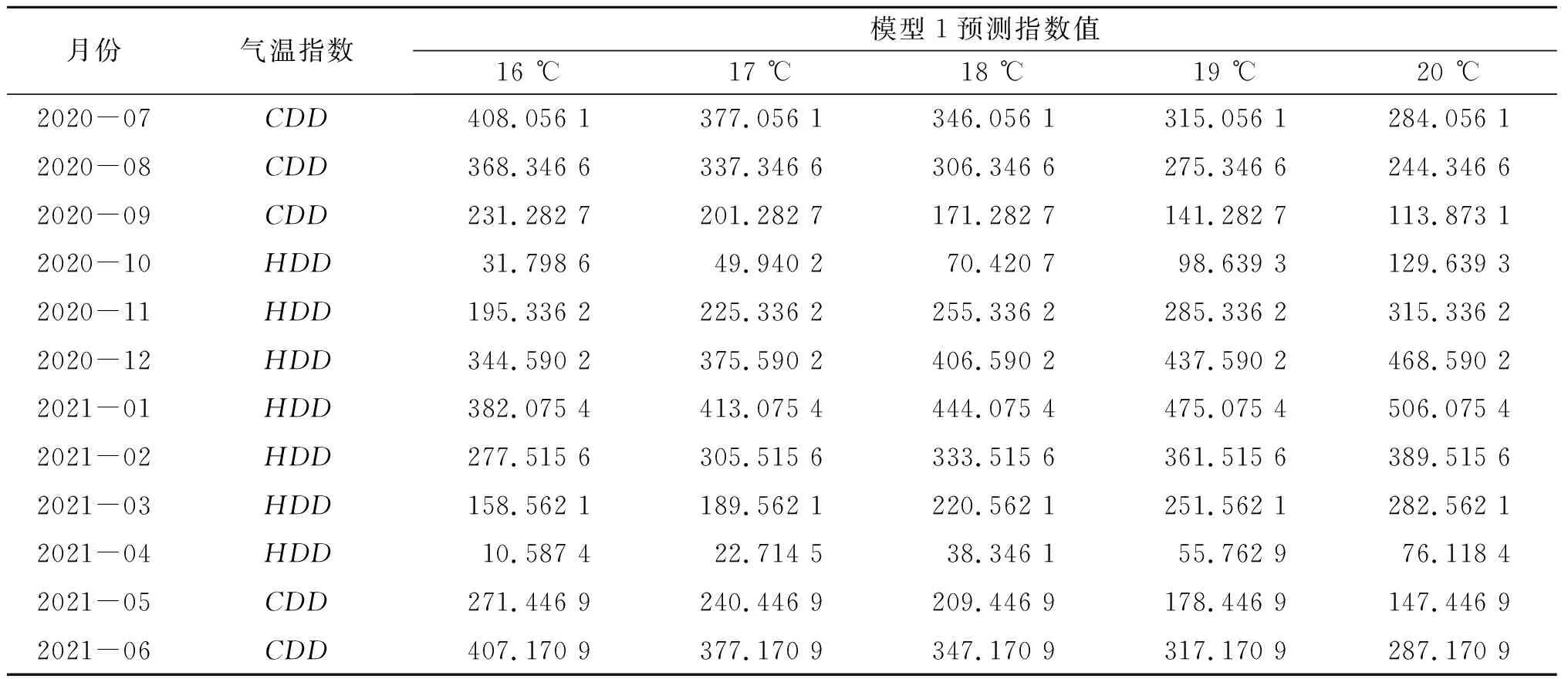
表6 不同基准温度下的预测指数值Tab.6 Forecast index value at different baseline temperatures

由表5和表6可以得到不同基准温度下,期限为3,6,9,12个月的真实和预测累计指数值,结果见表7和表8。

表7 不同基准温度下期限为3,6,9,12个月的真实累计指数值Tab.7 Actual cumulative index value of 3,6,9,12 months at different baseline temperatures

表8 不同基准温度下期限为3,6,9,12个月的预测累计指数值Tab.8 Forecast cumulative index value of 3,6,9,12 months at different baseline temperatures

根据式(9)计算不同基准温度下期限为3,6,9,12个月的真实和预测累计指数值的相对误差率,结果见表9。

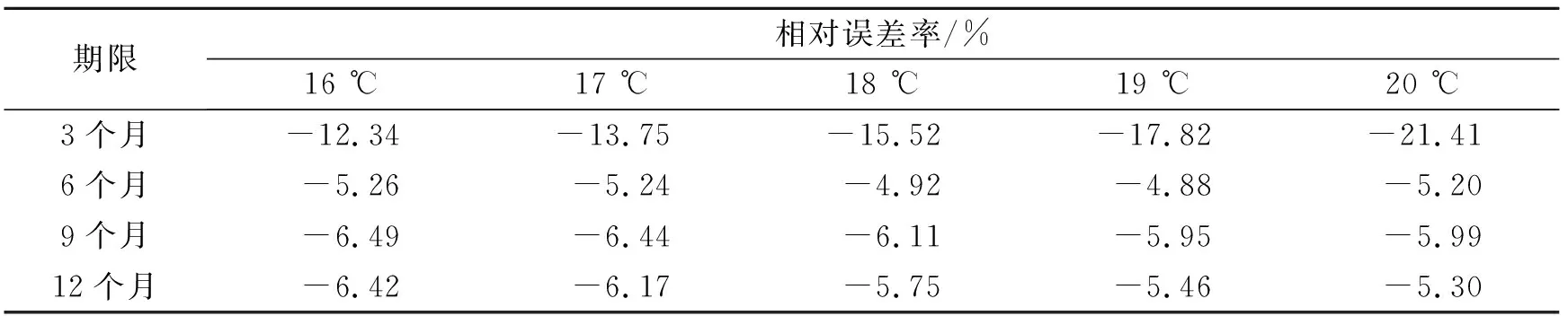
表9 不同基准温度下期限为3,6,9,12个月的相对误差率Tab.9 Relative error rate of 3,6,9,12 months at different baseline temperatures

从表7～表9可知,在不同基准温度下,模型1得到的期限为3,6,9,12个月的预测累计指数值均高于真实值；相对误差率绝对值最大为21.41%,最小为4.88%。总体来看,预测累计指数值较为接近真实值,这也就是说明模型1的预测计算结果精度较高,稳定性较好,可以用于气温期权的定价。

假定标的指数为HDD欧式看涨期权和CDD欧式看跌期权的合约,K为执行价格,r为无风险利率,名义价值为Q,合约时间为〈t1,t2〉,同时假定风险中性世界中的风险市场价格为 0。此时,HDD欧式看涨期权和CDD欧式看跌期权的价格分别按照计算。

cHDD(t1,t2,K)=e-r(t2-t1)×Q×max(HDD-K,0)，

(10)

pCDD(t1,t2,K)=e-r(t2-t1)×Q×max(K-CDD,0)

(11)

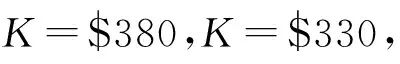
表10 不同基准温度下8月份和12月份的预测期权价格的结果Tab.10 Results of forecast option prices in 8 and 12 months at different baseline temperatures

表10中,在基准温度为18 ℃ 时,有

从表10可以看出,随着基准温度的升高,预测期权的价格越来越高,当基准温度为 20 ℃ 时,价格最高,这也说明基准温度对气温期权价格有显著影响。

4 结论

本文基于郑州市气温问题,建立了两区域转换模型和单区域均值回复模型。模型参数的估计部分,采用EM算法高斯混合模型对参数进行估计,然后分别预测郑州市2020年7月1日至2021年6月30日的日平均气温并与真实气温进行对比分析。通过对比发现,使用蒙特卡洛模拟方法模拟100 000次后,一个均值回复和一个布朗运动模型预测的日平均气温更接近真实的日平均气温数据,区域转换模型1可以很好地拟合郑州气温的随机变化。

最后,对于具有一个均值回复和一个布朗运动的区域转换模型，计算了不同基准温度下期限为3,6,9,12个月的真实数据和预测累计指数值,并计算其相对误差率,验证了模型1预测的计算结果精度较高,稳定性较好。此外，还进行了不同基准温度下的定价研究。

实证分析结果也验证了ELIAS R S等[3]的结果：一个均值回复和一个布朗运动的区域转换模型，是一个适用于描述气温随机特征的有效的区域转换模型。但是同时说明,由于全球气候的多样性,区域转换模型不一定就是唯一的最优模型。对不同城市进行天气衍生品的定价，需要根据当地气温数据进行实证分析研究,建立描述不同城市或者地区气候特征的准确的气温模型。