从错排问题到匹配问题

刘 倩

(西安电子科技大学 数学与统计学院，陕西 西安 710071)

0 引言

在大学概率论课程中，匹配问题利用一般加法公式易于解决，但是在教学过程中，我们会先想到利用对立事件直接求解对立事件包含的有利场合数，即“全部错排”数。这是由于受到高中阶段排列组合思维的影响。关键问题是,错排数目很容易就能计算出来吗？本文从一道高考错排问题谈起，讨论错排数目的递推公式，再扩展到匹配问题，讨论匹配问题的数学期望，即平均配对个数，最后进一步将匹配问题的条件加强，讨论多项匹配问题。

1 错排问题

近年来，全国高考试题注重了对考生能力和素质的考查，试题设计增加了贴近日常生活的应用型案例，其中的“贺卡问题”就属于这方面的一道题。

例1(贺卡问题[1])同室4人各写一张贺年卡，先集中起来，然后每人从中拿一张别人送的贺年卡，则4张不同的贺年卡不同的分配方式有

A. 6种 B. 9种 C. 11种 D. 23种

这个问题情境新颖，无法直接套用公式、法则，主要考查加法或乘法原理或从反面考虑(排除法)的思想方法，考查分析问题与解决问题的能力。

“贺卡问题”实际是被著名数学家欧拉称为“组合数论的一个妙题”的“装错信封问题”的一个特例。“装错信封问题”是指：一个人写了n封不同的信及相应的n个不同的信封，他把这n封信都装错了信封，问都装错信封的装法有多少种? 这个问题是由当时最有名的数学家约翰·伯努利的儿子丹尼尔·伯努利提出来的。这道高考题就是以组合数学中著名的“错排问题”为背景，用生活实例设计问题，十分新颖。

例2(错排问题[2])有n个正整数1，2，3，…，n，将这n个正整数重新排列，使其中的每一个数都不在原来的位置上，这种排列称为正整数1，2，3，…，n的错排，问这n个正整数的错排个数是多少?

瑞士著名数学家欧拉按一般情况给出了一个递推公式，

D(n)=(n-1)(D(n-2)+D(n-1)),

(1)

特殊地，D(1)=0，D(2)=1。

可以用一个直观的例题理解该递推公式并最终得到错排数的通项公式。

例3(装错信封问题)用A，B，C，…表示写着n位友人名字的信封，a，b，c，…表示n份相应的写好的信纸。把错装的总数为记作D(n)。假设把a错装进B里了，包含着这个错误的一切错装法分两类：

1) b装入A里，这时每种错装的其余部分都与A、B、a、b无关，应有D(n-2)种错装法。

2) b装入A、B之外的一个信封，这时的装信工作实际是把(除a之外的)n-1份信纸b，c，…装入(除B以外的)n-1个信封A，C，…，显然这时装错的方法有D(n-1)种。

总之，在a装入B的错误之下，根据加法原理，共有D(n-2)+D(n-1)种错装法。

a装入C，装入D……的n-2种错误之下，同样都有D(n-2)+D(n-1)种错装法，根据乘法原理，n个不同元素的错排数递推公式为D(n)=(n-1)(D(n-2)+D(n-1))。

有了递推公式，很容易得到错排数的通项公式

(2)

具体推导过程可参阅相关文献[1]。事实上，用上述方法解题，就是反复考虑包含与排斥的情形，这实际就是利用了容斥原理。基于上面的递推公式，贺卡问题的正确答案是B。

下面考察错排数公式的两个简单应用。

例4数1，2，3，…，9的全排列中，求偶数在原来位置上，其余都不在原来位置上的错排数目。

分析实际上，这是1，3，5，7，9五个数的错排问题，因此，错排数目是44。

例5对上述问题略加变化:数1，2，3，…，9的全排列中，求恰好有5个数不在原来位置上的排列数。

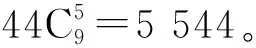
2 匹配问题

同样沿用上述装错信封问题进行探讨。

例6(匹配问题[3])一个人写了n封不同的信及相应的n个不同的信封，他任意地将这n封信装入n个信封中，问至少有一封信和信封是一致的概率是多少?

分析这个题目有多种解法。记Ai表示第i封信的信纸和信封一致，i=1,2,3,…,n,则所求概率为P(A1∪A2∪…∪An)。

解法1若直接计算有利场合数，无疑是十分复杂的。

解法2已知错排数通项公式(2)的情况下，利用对立事件进行求解。

从而概率为

(3)

解法3相比前两种方法，采用一般加法公式P(A1∪A2∪…∪An)，直接求解：

…

所以，

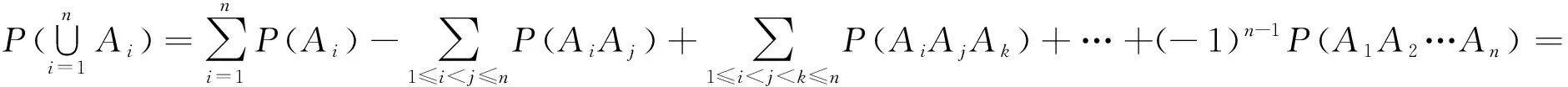
(4)

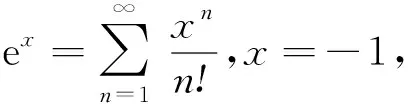
更进一步，计算平均匹配个数，即求放对的信封数X的数学期望和方差。这同样是一道易错题目。期望通过直接计算有利场合数，这无疑也是十分复杂的。针对复杂随机变量的数学期望求解，可以利用期望的可加性进行计算。

令

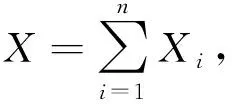
于是有

(5)

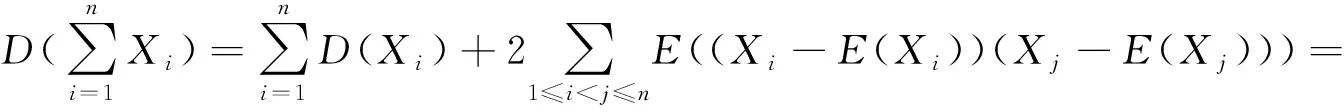
(6)

匹配问题中匹配数的数学期望与方差均为1，与信封个数n无关。

3 多项匹配问题[4]

例7有n个人填写一份登记表并交一张照片，现在把登记表及照片任意地装入n个有姓名的档案袋中(每袋只允许装入一份登记表及一张照片)，那么没有一袋的登记表及照片都装对的概率是多少？进而这种场合下，错排数是多少？

解记Ai表示第i袋的登记表和照片都一致，i=1,2,…,n，利用一般加法公式(4)，得

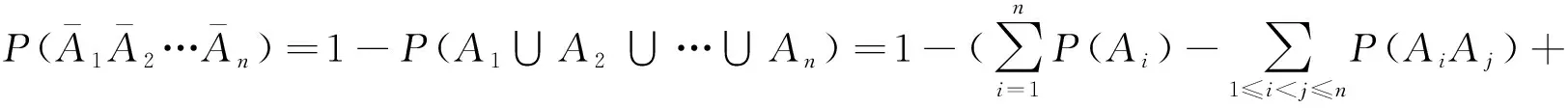
(7)

其中,

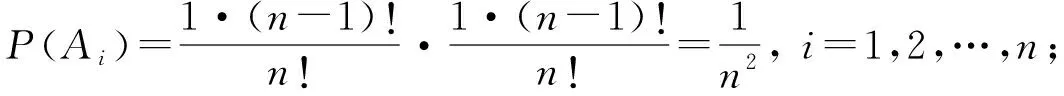
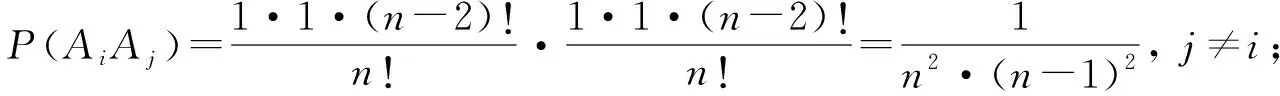
代入公式(7)，得到

(8)

利用公式(2)和(8)，得到该多项配对问题中的错排数目为

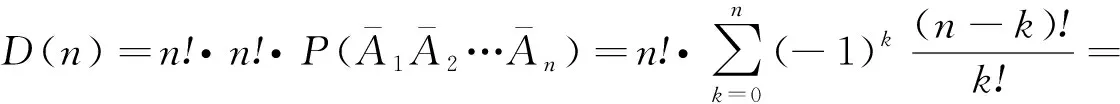
(9)

当n=3，完全错装的概率是13/18，此时，完全错装的方法一共有26种。

4 结论

在概率论课程中，古典概型是一个学习的难点。本文以匹配问题为研究对象，探讨其不同解决方法之间的关系。我们发现大部分同学会想到对立事件，即解决“n个不同元素全部错排问题”，与利用一般加法公式进行计算，取对立后得到的结果是一致的。显然，利用一般加法公式的求解要更加方便。这就是为什么在大学的概率论课程体系中，我们在引入概率的公理化定义之后，会系统学习概率的性质并引入概率论中几个重要的公式，比如全概率公式、贝叶斯公式。这些公式的共同特点就是可以解决复杂的古典概型问题[5-6]，因此在学习概率论时，要特别提醒学生注意概率论的各个基本概念和理论是怎样运用到实际生活中的。