连接件对钢板混凝土组合墙轴压性能影响试验*

刘阳冰 王 爽 刘晶波 曹天峰

(1.南阳理工学院土木工程学院，河南南阳 473004；2.清华大学土木工程系，北京 100084；3.重庆大学土木工程学院，重庆 400045)

双钢板混凝土组合墙是在置于外侧的两片钢板中填充混凝土而形成，其中外钢板和混凝土之间设置抗剪连接件，连接件通常为栓钉和两端均焊接于钢板上的对拉钢筋，混凝土内不再配置任何钢筋。由于抗剪连接件的存在，内部混凝土能在一定程度上抑制外钢板过早局部屈曲；同时，两侧钢板对内部混凝土的开裂和压溃起到有效的限制作用。组合墙能充分发挥钢板和混凝土两种材料的承载能力；外钢板可以避免混凝土裂缝外露，提高结构的正常使用性能和耐久性能，并可以促进高强度混凝土的使用。在我国CAP1000核电机组示范工程中，钢板混凝土组合墙结构大量用于反应堆厂房内部结构模块和其他核安全相关结构模块中[1-3]。近年来钢板混凝土组合墙逐渐应用于民用建筑，已成为工程研究的热点[4]。

连接件形式和布置方式的不同会影响钢板混凝土组合墙的受力和变形性能，连接件不仅增强了钢板与混凝土之间的黏结力，而且还可以防止钢板过早屈曲，从而保证钢筋和混凝土两者共同发挥作用。文献[1，5]完成了8片钢板混凝土组合墙的轴压试验，研究了不同距厚比(连接件间距与外钢板厚度比值)对组合墙受力、变形和破坏形态的影响规律，并推导了防止组合墙发生弹性局部屈曲的距厚比限值设计公式。文献[6]在总结钢板混凝土组合剪力墙各类连接件优缺点的基础上，提出了两种新型的L形连接件和C形连接件；并对4片高剪跨比钢板混凝土组合剪力墙进行了低周反复试验，研究两种连接件对组合钢板剪力墙抗震性能的影响。文献[7]对4片设有栓钉和对拉螺栓的组合墙进行了低周反复试验，研究了试件的破坏形态、变形和刚度退化等特性。文献[8]以实际工程为原型，完成了1/4缩尺模型的双钢板混凝土组合剪力墙试件和内置钢板混凝土组合剪力墙的轴压性能试验，并提出了钢板混凝土组合剪力墙轴压承载力的计算公式。文献[9]进行了4个应用于核电工程的钢板混凝土组合墙轴压试验，分析了距厚比对构件承载力和变形性能的影响。文献[10]通过有限元数值模拟，分析了抗剪连接件对钢板混凝土组合墙外钢板局部屈曲和组合作用的影响规律。

已有研究对连接件距厚比对钢板混凝土组合墙局部屈曲性能的研究较多，但是较少涉及连接件组合形式不同对组合墙性能的影响研究。本文在已有钢板混凝土组合墙试验研究的基础上，设计了4个钢板混凝土组合墙试件，研究栓钉和对拉螺栓相对数量不同对组合墙轴压性能的影响。

1 试验概况

1.1 试件设计

根据文献[1]试验结果和试验分析，对于采用Q235钢的双钢板混凝土轴心受压构件，基于欧拉公式，当连接件间距和钢板厚度比值(距厚比)小于等于35时，钢板发生屈服先于弹性屈曲的破坏。因此，为了保证外钢板不发生局部弹性屈曲的前提下，墙钢板距厚比采用30，侧钢板距厚比采用12，设计了4个钢板混凝土组合墙轴心受压试件，4个试件的连接件间距和位置均相同，但连接件形式不同，墙钢板厚度均为3 mm；侧钢板厚为8 mm，连接件均为焊接栓钉；墙钢板连接件为焊接栓钉和对拉螺栓两种，每个试件焊接栓钉和对拉螺栓的总数量相同，但相对比例不同，分别为3∶1、1∶1、全部为栓钉、全为对拉螺栓，试件信息如表1所示。

表1 试验试件编号及基本信息

4个试件总高度为1 300 mm，混凝土厚度为160 mm，墙净尺寸为800 mm×716 mm×166 mm，试件设计图和实际构件如图1所示。为了便于观察试验现象，在制作好的试件外钢板上喷上灰色油漆，并画好90 mm×90 mm白色网格。

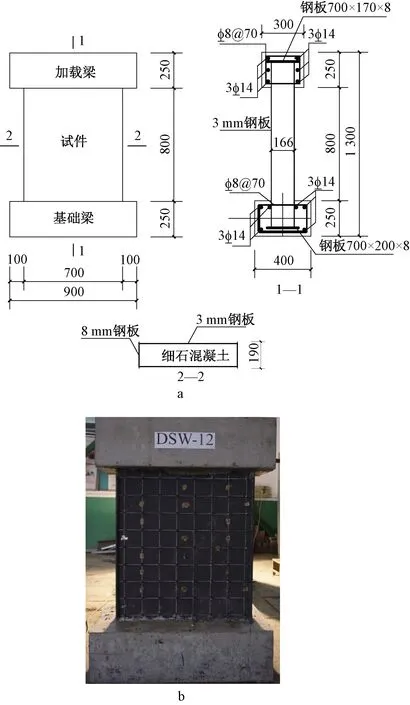
a—试件设计示意；b—实际构件。

4个组合墙四周均焊接8 mm的钢板，用来约束墙体，并在上钢板、侧钢板及下钢板上预留直径为100 mm的洞口，用来浇筑混凝土和保证混凝土浇筑密实。焊接成的空心钢板墙尺寸均为1 216 mm×716 mm×166 mm，其中顶部和底部208 mm分别插入上部加载梁和下部的基础梁中，钢板钢材为Q235钢，混凝土为C50细石混凝土，焊接栓钉和对拉螺栓直径均为6 mm。以DSW-10为例，图2给出钢板连接件分布形式、箍筋预留孔以及加工后的钢构件部分。图中·代表直径为6 mm的对拉螺栓，+代表直径为6 mm、长度为48 mm的栓钉。墙钢板上预留直径为10 mm的洞口用于穿基础梁和加载梁中的箍筋。所有洞口均位于加载梁和基础梁的高度范围内，不影响组合墙的受力性能。

a—墙钢板和侧钢板设计示意；b—加工成型示意。

1.2 试验方法

试验前，按照规范规定方法[11-12]对钢材和混凝土的力学性能进行测试。3 mm厚钢板钢材屈服强度和屈服应变为276 MPa和0.13%，极限强度和极限应变分别为412 MPa和21.08%；8 mm厚钢板钢材屈服强度289 MPa和屈服应变为0.15%，极限强度和极限应变分别为429 MPa和22.59%。4个试件分两批次浇筑混凝土，在每一批试件浇筑时，同时制作边长为150 mm×150 mm×150 mm的混凝土标准立方体试件，并与试件在相同的环境条件下进行养护。试件DSW-9和DSW-10为第一批，混凝土立方体强度fcu平均值为50.4 MPa，试件DSW-11和DSW-12为第二批，混凝土立方体强度fcu平均值为48.6 MPa。

试验加载采用微机控制电液伺服20 000 kN压剪试验机对试件施加轴向压力，试件上作用的压力值可由试验机数据采集系统直接读取；两个位移计布置在加载梁和基础梁之间，测量试件的竖向位移，如图3a所示。为了观测墙钢板的变形，在一个试件的正面和背面墙钢板对应位置，布置竖向和横向应变片，如图3b所示。加载方法采用文献[3]中力和位移控制单调轴向加载。

a—实际加载；b—加载装置示意和墙钢板应变片布置，mm。

2 试验现象及分析

2.1 试验现象

试件DSW-9：加载至3 700 kN时，背面钢板向外凸出，发生局部屈曲，如图4a所示。荷载达到6 480 kN时，背面钢板屈曲水平向贯通。加载至6 650 kN，构件发出连续的响声，正面和背面钢板竖向位移和面外局部变形持续发展，出现折痕，侧焊缝未被拉开，如图4b所示。破坏发生时，侧焊缝拉开，侧面钢板面外变形急剧增加，正面和背面钢板产生褶皱，内部压碎混凝土从缝隙流出，构件承载力急剧下降，构件破坏，如图4c所示。

a—背面钢板首次屈曲；b—背面贯通屈曲；c—破坏时背面钢板。

试件DSW-10：荷载达到4 000 kN时，正面墙钢板面外凸出，发生局部屈曲，如图5a所示；5 000 kN时，正面钢板底部形成横向贯通屈曲，如图5b所示。5 050 kN时，正面顶部部分对拉螺栓外伸部分弯曲。5 700 kN时，局部变形范围增大，如图5c所示。5 900 kN时，试件发出响声，部分对拉螺栓断裂，可以从试件中拔出，随后随着荷载的增加，断续听到对拉螺栓断裂声，部分螺帽崩出。荷载达到6 650 kN时，构件发出连续的响声，正面和背面钢板受压变形持续发展，直至部分侧焊缝被拉裂，侧钢板急剧外凸，墙钢板产生褶皱，从裂缝中可见内部混凝土已被压碎，构件破坏，如图5d所示。

a—正面钢板首次屈曲；b—正面钢板底部贯通局部屈曲；c—背面钢板屈曲；d—试件破坏。

试件DSW-11：加载前，敲击墙钢板，顶部附近有空洞声，上部混凝土浇筑不密实。空洞处从荷载2 500 kN开始逐渐出现钢板面外凸出，荷载达到5 840 kN时，背面和正面钢板底部和顶部之间形成水平贯通屈曲，如图6a所示。6 300 kN时，构件发出连续的响声，部分侧焊缝被拉裂，侧钢板急剧外凸，墙钢板产生褶皱，从裂缝中可见内部混凝土已被压碎，构件破坏，如图6b、6c所示。

a—背面贯通屈曲；b—试件破坏(正面)；c—试件破坏(背面)。

试件DSW-12：试件加载梁不平整，最高相差约5 mm。加载至2 300 kN时，敲击有空洞声，但未发现钢板外凸。3 000 kN时，可观察到空洞处钢板轻微外凸，如图7a所示。5 000 kN时，部分对拉螺栓被拉断，不断发出断裂声。5 500 kN正面局部屈曲位置，对拉螺栓断裂，与混凝土脱离，很容易拔出。随着荷载的增大，钢板各个局部屈曲部位变形继续向平面外发展，构件不时发出响声，图7b给出6 000 kN时正面钢板局部屈曲情况。但总体来说，其平面外变形小于试件DSW-9～DSW-11。荷载达到6 300 kN时，构件发出连续的响声，正面和背面钢板受压变形持续发展，位移不断增大，直至部分侧焊缝被拉裂，侧面钢板急剧外凸，正面和背面钢板产生褶皱，从裂缝中可见内部混凝土已被压碎，构件破坏，如图7c所示。

a—背面钢板首次屈曲；b—正面钢板局部屈曲；c—试件破坏。

4个试件在侧焊缝拉开前，侧钢板均未观测到明显的面外变形，敲击侧钢板均未听到空洞声，说明侧钢板在焊缝拉开前与混凝土没有明显分离，均未发生局部屈曲。

2.2 试验现象分析

图8为4个试件的荷载-位移曲线，4个试件的初始刚度基本相同，在轴向压力5 000 kN前，各试件的整体刚度几乎不变，DSW-9和DSW-10发生钢板局部屈曲的荷载比较接近，其屈曲荷载和最大承载力均大于DSW-11和DSW-12。另外，钢板首次发生屈服或屈曲时，荷载-位移曲线斜率无明显改变，钢板屈服或屈曲对试件整体刚度影响不大。

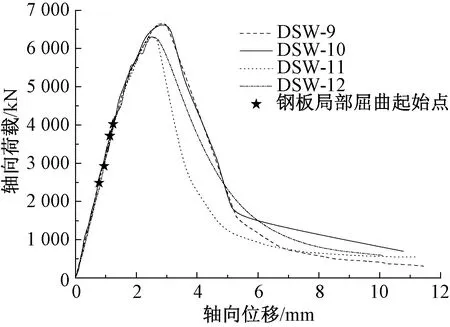
图8 荷载-位移曲线

试验得到DSW-9～DSW-12钢板发生屈曲时，平均轴向应变(竖向位移计在屈曲时的读数的平均值/试件高度)分别为0.142%、0.155%、0.097%和0.118%。由材料力学性能试验可知墙钢板钢材的屈服应变为0.13%，试件DSW-9、DSW-10钢板发生屈曲时，平均轴向应变大于钢板相应的屈服应变，因此钢板的屈服先于局部弹性屈曲。试件DSW-11、DSW-12钢板发生屈曲时，平均轴向应变小于钢板相应的屈服应变，因此这两个试件为钢板先发生屈曲，然后再屈服。

对于DSW-11和DSW-12，由于试件上部混凝土不密实、试验梁不平整等原因造成加载前试件偏心，影响试件的初始屈曲荷载，但对承载力影响不大。两个试件均在压应力叠加区域，钢板首先发生屈曲，局部屈曲部位的轴向应变要大于平均轴向应变。为了进一步分析钢板局部屈曲情况，图9给出4个试件首先出现局部屈曲位置或附近的钢板应变片测得的竖向应变和横向应变结果。

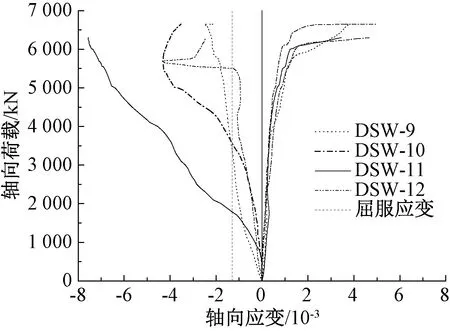
图9 钢板应变曲线

从图9中可以看出，DSW-9～DSW-11局部屈曲点处的竖向应变均在荷载达到屈曲荷载3 700，4 000，2 500 kN时，其应变大于钢材的屈服应变，钢板先屈服后局部屈曲。而DSW-12虽然钢板的竖向应变随着荷载的增加达到了钢材的屈服应变，但在屈曲荷载2 300 kN时，其应变小于屈服应变，钢板为先发生弹性屈曲而后屈服，且随着面外局部屈曲的发展，竖向应变在接近最大承载力时会急剧减小。如果构件偏心严重，基于欧拉公式得到的防止构件弹性屈曲先于屈服发生的距厚比限值并不能保证墙钢板屈服先于屈曲发生。总体上，4个试件横向应变在达到试件最大承载力前增长速度和变形值远小于纵向应变，且变化规律基本相同，这是因为竖向是试件的加载方向，且4个试件均观测到发生横向局部屈曲；荷载达到承载力90%左右时，横向变形急剧增大。

4个试件的破坏均为脆性破坏，除DSW-12外，破坏过程基本相同，先为墙钢板达到其材料屈服强度，然后发生局部屈曲，进而发展为水平贯通屈曲，混凝土压碎，侧焊缝拉开构件从而失去承载力。对拉螺栓的相对比例虽然对钢板混凝土组合墙的轴向受压刚度、受压承载力、钢板的局部屈曲荷载和破坏形态影响不大，但对面外局部变形有抑制作用。相同截面、距厚比试件，采用对拉螺栓的比例越高，破坏时钢板局部屈曲变形越小。

3 有限元数值模拟

3.1 有限元模型

采用有限元软件ABAQUS建立4个试件的有限元模型。模型主要包括：钢板、混凝土、栓钉、对拉螺栓、加载梁和基础梁。混凝土采用C3D8R实体单元，钢板采用S4R壳单元，栓钉采用SPRING2非线性弹簧单元，对拉螺栓采用绑定约束Tie单元模拟。采用结构化网格划分方法来划分网格，混凝土本构采用损伤弹塑性模型[13]，钢材本构采用二次流塑模型，栓钉剪力-滑移曲线采用Ollgaard曲线[14]。钢板和混凝土之间并设置接触单元来模拟钢板与混凝土的界面模型。混凝土与钢板两者界面的法向接触和切向粘接滑移，通过定义接触来模拟。由于钢板与混凝土可以相互分离但不能相互渗透，法线方向的力能够完全传递，可采用“硬接触”来模拟。切向方向的上的接触，采用库仑摩擦模型[15]，在达到一定的临界值之前，认为界面传递的剪力τf与法向应力P成正比。用公式表示如下：

τf=μfP≤τbond

(1a)

τbond=0.75×[2.314-0.019 5×(B/t)]

(1b)

式中：μf为界面摩擦系数，取0.6[16]；τbond为界面临界剪力；B为钢板的边长，取B=(ab)1/2；t为钢板厚度；a、b分别为矩形钢板相邻的两边长。

基础梁的底面设置为固定端，在加载梁中心点的正上方设置参考点，把参考点与加载梁顶面进行耦合，采用对参考点进行位移加载的方式进行轴向荷载加载。有限元模型和加载方式如图10所示。

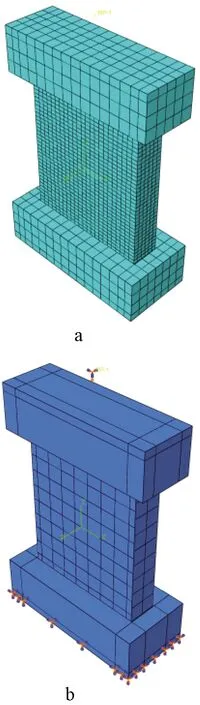
a—有限元模型；b—加载方式。

3.2 有限元与试验结果对比

分别对4个试件的破坏形态和加载全过程曲线进行了有限元模拟。图11给出试件有限元计算得到的荷载位移曲线与试验曲线的对比。从图中可以看出试验曲线的刚度均低于有限元的计算结果，模拟得到最大承载力与试验值较为接近，但位移值相对偏小。除了由于试件制作、材料的不均匀、加载中的偶然偏心等造成的非精确轴心加载外，模拟时对拉螺栓直接采用的是钢板和混凝土在相应的节点上耦合，未考虑其在试验过程中与混凝土和钢板的滑移以及破坏，这些都造成计算位移偏小，刚度偏大。

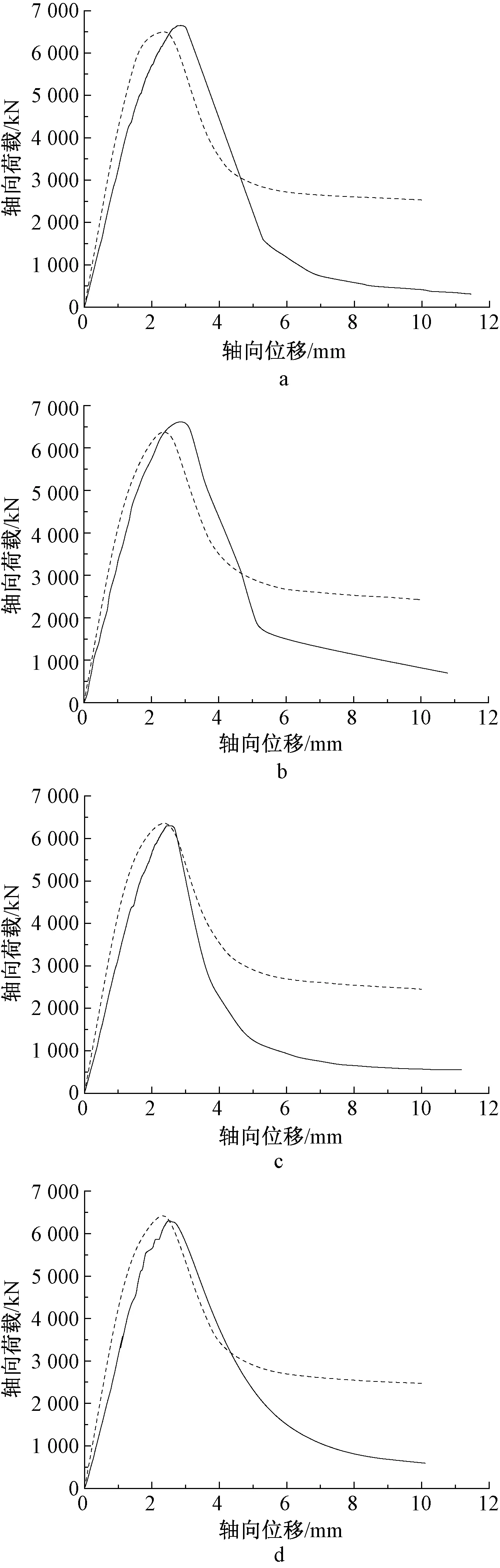
a—DSW-9；b—DSW-10；c—DSW-11；d—DSW-12。

表2对文献[1]的试件DSW-1～DSW-8和本文的DSW-9～DSW-12共计12个双钢板混凝土组合墙试验得到的构件的最大承载力与有限元分析结果的对比。从表中数值可以看出，两者误差相差不大，最大误差为12.6%。其中DSW-6、DSW-7、DSW-11和DSW-12试验得到的最大承载力小于有限元分析结果，这主要是因为试件制作误差以及加载偶然误差，其中DSW-11混凝土浇筑不密实，DSW-12加载梁浇筑不平导致初始偏心，使承载力偏小。

表2 极限承载力对比

图12为试件破坏形态的对比。图中有限元模拟结果为试件达到破坏荷载时墙钢板的面外位移云图。有限元模拟得到的试件破坏和局部屈曲位置集中在试件上部，这是因为数值模拟时试件下端边界条件为固定端，组合墙下半部分受到约束。总体来说，试件的破坏部位与模拟结果相近，模拟与试验结果吻合较好。4个试件仅栓钉的布置形式和对拉螺栓的相对比例不同，连接件形式对试件最终破坏形态和承载力影响不大。从图中可以看出，试件破坏时，钢板的面外位移DSW-12最小，DSW-11最大，DSW-9和DSW-10介于两者之间，其中DSW-12的剪力连接件全为对拉螺栓，DSW-11为全栓钉，DSW-9和DSW-10对拉螺栓和栓钉按一定比例布置，由此可知，对拉螺栓对钢板面外变形的发展有明显的抑制作用。

a—DSW-9；b—DSW-10；c—DSW-11；d—DSW-12。

3.3 参数分析

为了进一步分析对拉螺栓和栓钉比例不同对双钢板混凝土组合墙轴向受力性能影响，采用有限元软件对不同的有限元模型进行轴向受力全过程的参数分析。模型墙高均为1 200 mm，内部混凝土截面尺寸为200 mm×800 mm，混凝土强度等级为C30；墙钢板厚5 mm，侧钢板厚8 mm，钢板采用Q235；连接件间距为90 mm，距厚比为18。连接件共12排9列。对拉螺栓和栓钉按比例间隔布置，比例分别为：1∶2、1∶5、1∶8、1:11、2∶1、5∶1、8∶1、11∶1、全为对拉螺栓和全为栓钉，共10个模型。由于计算得到的部分模型荷载-位移曲线重合，因此给出具有代表性的其中5个模型的轴向荷载位移曲线如图13所示。

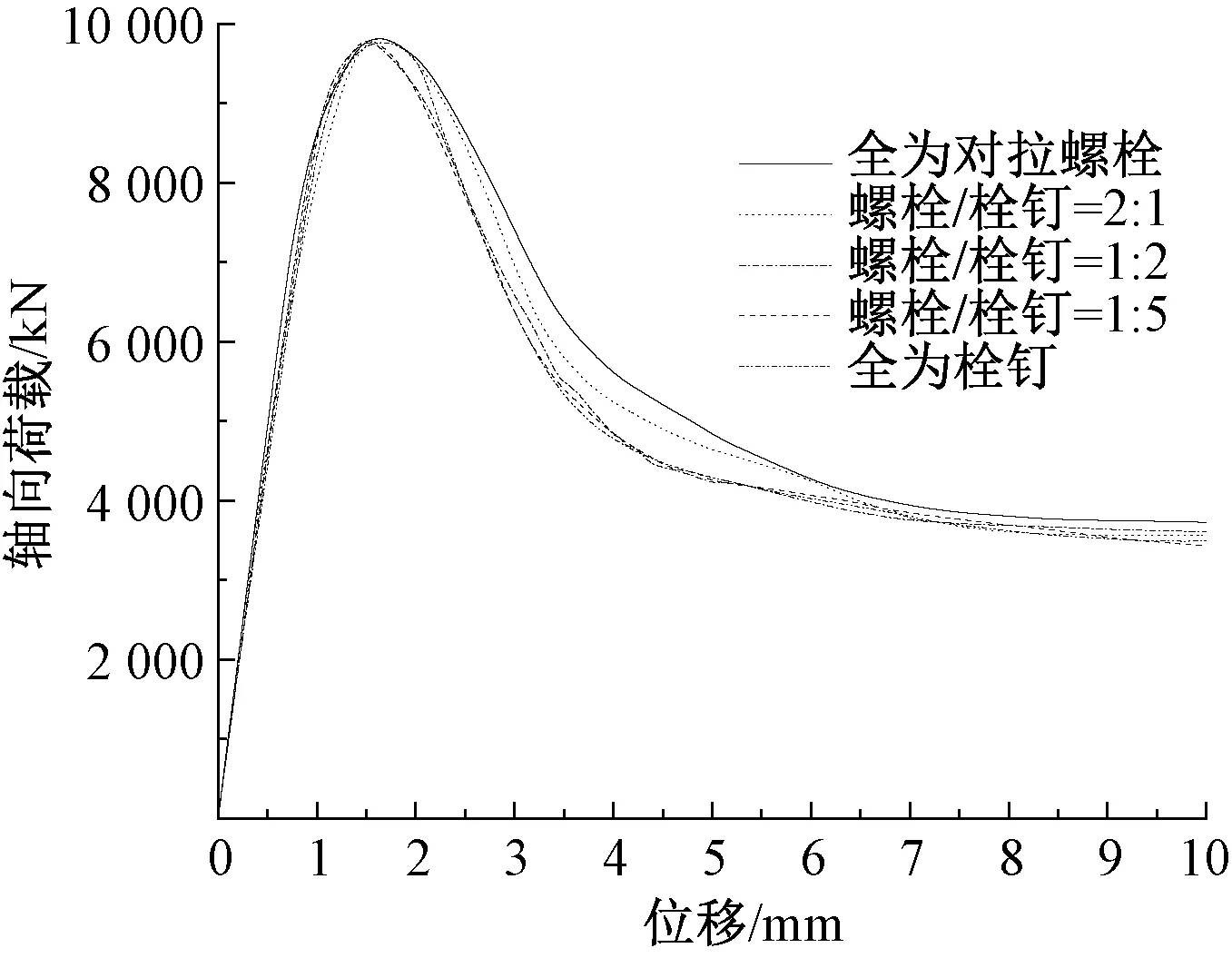
图13 参数分析结果

从图13可以看出，模型其他参数不变，只改变连接件对拉螺栓和栓钉的比例，5个模型得到的最大承载力基本相同。加载初期，模型的初始刚度基本相同，随着荷载的增加，连接件全为栓钉模型的刚度最小，全为对拉螺栓的模型刚度最大，其他3个模型介于中间。总得来说随着对拉螺栓数量的增多，刚度略微增大。螺栓和栓钉比例为1∶2、1∶5和全为栓钉的3个模型的荷载和位移曲线几乎重合，全为螺栓和螺栓和栓钉比例为2∶1的两个模型荷载位移曲线上升段也几乎重合。且由有限元分析可知，5个模型出现局部屈曲的荷载也基本相同均在9 000 kN左右，且均发生屈服先于屈曲的的破坏。

综合以上试验和参数分析结果，双钢板混凝土组合墙在距厚比保证不发生局部屈曲先于屈服破坏的情况下，距厚比相同，连接件中对拉螺栓和栓钉的相对比例对组合墙承载力和竖向变形影响不大，但对拉螺栓在一定程度上可以减少局部屈曲发生时的面外变形和加强整体刚度。且在实际工程中，对拉螺栓连接件施工不便，常采用在两钢板件焊接对拉钢筋来代替，对拉螺栓数量过多会影响墙内部混凝土的浇筑和振捣，难以保证混凝土密实性。因此，建议对拉螺栓的数量小于栓钉数量，但不能过少，建议两者之比为1∶2为宜，按比例间隔布置。

4 结 论

对4个钢板混凝土组合墙进行了轴压试验和有限元数值模拟，分析了连接件形式不同对钢板混凝土组合墙受力、变形和破坏形式的影响。得到如下结论：

1)4个试件的破坏均为脆性破坏，除DSW-12外，破坏过程基本相同，墙钢板首先发生屈服，然后出现局部屈曲，进而发展为水平贯通屈曲，混凝土压碎，侧焊缝拉开构件从而失去承载力。

2)钢板发生屈服或局部屈曲时，荷载-位移曲线斜率无明显改变，钢板出现屈服或面外屈曲时对试件整体刚度影响不大。

3)对拉螺栓的相对比例对钢板混凝土组合墙的轴向受压刚度、承载力、钢板的局部屈曲荷载和破坏形态影响不大，但对局部变形有抑制作用。相同截面、距厚比试件，采用对拉螺栓的比例越高，破坏时钢板局部屈曲变形越小。

4)对试件进行了加载全过程的有限元数值分析，对比了荷载-位移全曲线，总体上数值模拟的试件初始弹性刚度要大于试验结果，最大承载力相差不大。模拟所得试件破坏形态也与试验结果较为吻合。数值模拟方法的参数设置合理，分析方法可行，为进一步开展钢板混凝土组合墙受力和变形性能影响因素参数分析奠定了基础。