再生混凝土疲劳可靠度及疲劳寿命预测*

钟楚珩 龙宇华 周金枝,2 吴维熙

(1.湖北工业大学土木建筑与环境学院，武汉 430070；2.桥梁结构健康与安全国家重点实验室，武汉 430034)

近年来我国基建的发展快速，产生了许多建筑垃圾，将其随意堆弃会影响市容和交通安全，且建筑垃圾里含有有害物质，传统的填埋方法会导致土地的浪费和土壤生态环境的破坏[1]。因此，对建筑垃圾的回收利用是当前研究的重点。在一些发达国家，对建筑垃圾的再利用已经到了实用化阶段，而我国对建筑垃圾的再生利用仍处于室内研究阶段[2-3]。对建筑垃圾制成的再生混凝土进行研究对环境保护具有较大的实际意义[4]。由于再生骨料存在孔隙多、吸水率高、表面覆盖的旧砂浆导致强度较低等问题，导致再生骨料混凝土在应用中出现了强度低、收缩率大、耐久性较差、变异性较高等问题，因此对再生混凝土的研究还存在许多亟待解决的部分[5]。如今对再生混凝土的研究多集中于物理力学性能等方面[6-7]，也有许多学者对再生混凝土的耐久性进行了研究[8-11]。国内外对普通混凝土弯曲疲劳性能已有了大量的研究[12-13]，但国内对再生混凝土疲劳性能的研究仍处于发展阶段。

肖建庄等对再生混凝土的弯折疲劳性能进行了试验研究，并基于损伤理论提出了一种简单实用的弯折常应力幅疲劳荷载作用下的再生混凝土疲劳模型[14]；朱红兵等研究了再生混凝土在抗折疲劳中断面破坏的两种形态，得出了再生混凝土疲劳寿命随再生粗骨料取代率的提高而降低的结论[15]；Arora等研究了不同取代率的再生混凝土的抗弯疲劳性能，改良了用于预测普通混凝土疲劳强度的计算式，使其可适用于再生混凝土，并得出了掺入少量矿物掺和料有利于提高再生混凝土抗弯疲劳性能的结论[16]。然而，现有的研究在再生混凝土疲劳可靠度与预测疲劳寿命的对比分析等方面并不充分。

因此，本研究对普通混凝土(NAC)和再生混凝土(RAC)进行疲劳试验，依据两参数Weibull分布对疲劳结果进行检验，再假设对数疲劳寿命服从对数正态分布，以Palmgren Miner疲劳损伤模型为基础，对NAC和RAC的疲劳可靠度进行计算；并在疲劳寿命服从Weibull分布和对数正态分布的两种假设下，对不同可靠度下的预测疲劳寿命进行比较分析。

1 再生混凝土抗折疲劳试验

1.1 试验材料及配合比设计

水泥采用P·O 42.5级普通硅酸盐水泥，其7 d抗压强度为25.9 MPa，抗折强度为4.5 MPa，28 d抗压强度为49.8 MPa，抗折强度为8.95 MPa。粗骨料包含天然粗骨料(NCA)和再生粗骨料(RCA)，RCA的原料为武汉市某工程中的拆除的路面板，其吸水率在24 h时达到最大值9.49%，粗骨料各项物理性能指标见表1。细骨料为细度模数2.65 mm的普通江砂和细度模数3.10 mm的机制砂。粉煤灰为I级粉煤灰，细度为8.0%，含水量为5.0%。矿粉为S95矿粉，密度为2.9%，比表面积为426 m2/kg，28 d混合砂浆活性指数为103%。减水剂为高性能聚羧酸减水剂。混凝土试件采用再生骨料取代率为30%制备，配合比见表2，其中NAC和RAC的坍落度分别为192，165 mm。每组分别制备6个标准立方体试件进行立方抗压和劈裂抗拉试验，12个标准棱柱体试件进行抗折试验和弯曲疲劳试验，共计36个试块。

表1 粗骨料物理性能

表2 NAC和RAC配合比设计

NAC和RAC的立方抗压强度、劈裂抗拉强度和抗弯强度如图1所示。可见，RAC的平均立方抗压强度比NAC小21.17%，RAC的平均劈裂抗拉强度比NAC小16.34%，RAC的平均抗弯强度比NAC小11.44%。这是由于再生粗骨料外表面包裹旧砂浆，新旧砂浆黏结较薄弱使得RAC试件内部存在初始裂缝，致使RAC强度相对于NAC大大降低。因此可预估RAC的疲劳抗弯性能较NAC差。

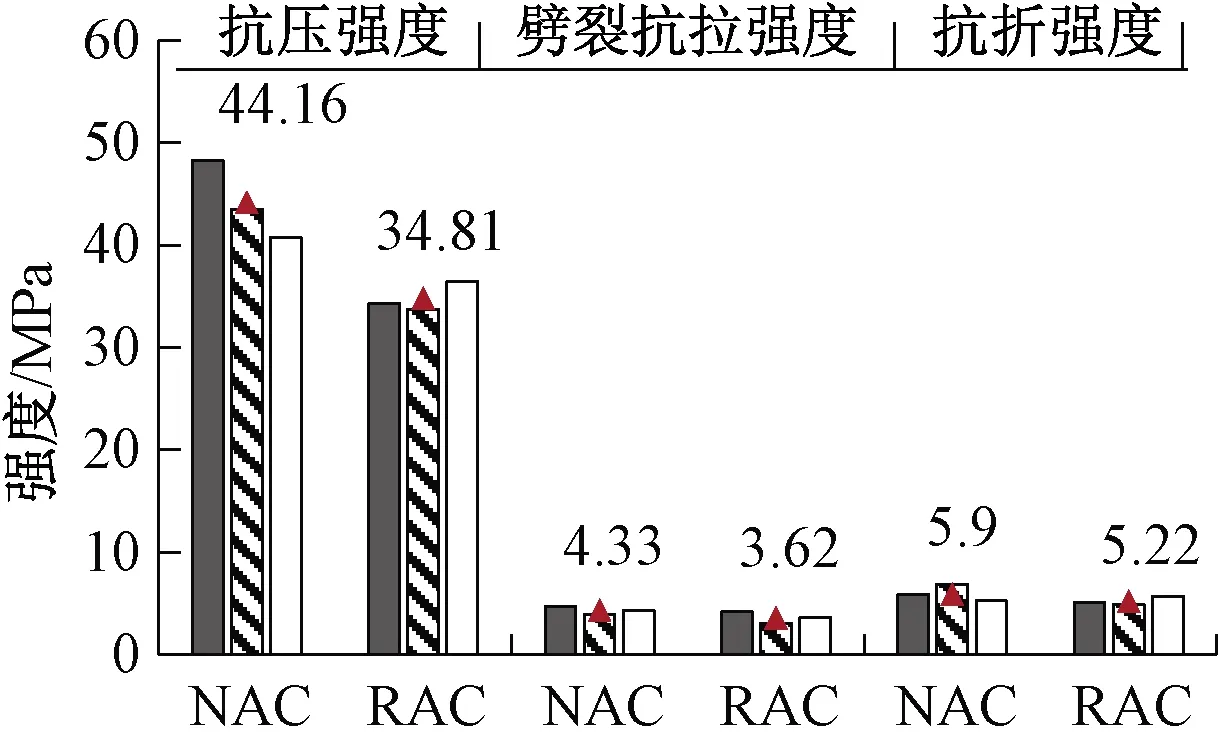
试件1；试件2；试件3；均值。

1.2 试验方案

根据GB/T 50081—2002《普通混凝土力学性能试验方法标准》的规定将试件放入相对湿度在95%以上，温度为(20±2)℃的标准养护室进行养护。28 d后取出进行弯曲疲劳试验。

弯曲疲劳试验采用MTS Landmark疲劳试验机及东华DH-3817F动静态应变仪进行试验及数据采集。在疲劳试验机上使用特制工具，分别在应力水平S=0.6、0.7、0.9下进行三分点加载(S=F/Fu，其中F为加载时的循环荷载幅值，Fu为抗折试验测得的极限承载力)，如图2所示。当试件无法继续承载时停止循环加载，并分别记录NAC和RAC各试样在不同应力水平下的疲劳寿命和纵向应变值。

图2 疲劳试验机加载情况

2 试验结果与数据分析

2.1 疲劳试验结果

NAC和RAC的弯曲疲劳寿命如表3所示。相同应力水平下，NAC的弯曲疲劳寿命均远大于RAC，可知NAC的疲劳强度远大于RAC，这和RAC本身存在初始缺陷有关，其中的微裂纹和孔隙在疲劳荷载作用下，更易发生扩展与贯通，在此种情况下，RAC经历较少循环次数即发生破坏。随着应力水平升高，NAC和RAC的弯曲疲劳寿命减小，且当应力水平高达0.9时，NAC和RAC的疲劳寿命明显降低，说明高应力水平下，NAC和RAC都无法较好的服役。

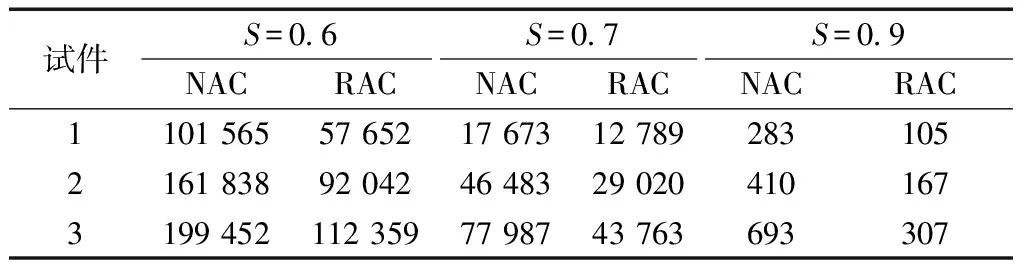
表3 NAC和RAC疲劳试验结果

2.2 再生混凝土的疲劳变形特征

试件在疲劳荷载作用下的变形可用ε-N曲线(应变-循环寿命曲线)进行表示，3种应力水平(S=0.6、0.7、0.9)下的ε-N曲线如图3所示。

图3 不同应力水平下NAC和RAC的应变随循环次数变化曲线

由图3可知，NAC和RAC在循环荷载作用下的变形都会经历三个阶段。第一阶段纵向变形发展迅速，之后随循环次数增加速率降低；第二阶段曲线较为平滑，且持续时间最长，是较为稳定的变形阶段，疲劳变形发展较缓；第三阶段疲劳变形骤增，历经较短的循环次数最终发生破坏。整个过程与裂纹发展规律类似，且在相同循环次数和应力水平下，NAC的纵向应变均小于RAC，说明RAC较NAC来说抗疲劳开裂能力较差。

2.3 再生混凝土抗折疲劳寿命Weibull分布检验

两参数Weibull分布的累计分布函数为[17]：

(1)

式中：Pf为失效概率；λ为形状参数，λ越大，混凝土的疲劳寿命离散性越小；Na为特征寿命，即存活率为36.8%时的寿命。

对式(1)两边取2次自然对数得到式(2):

(2)

将某一给定应力水平下疲劳试验得到的K个疲劳试验数据从小到大按顺序排列，序号为i，疲劳寿命N所对应的失效概率Pf为：

(3)

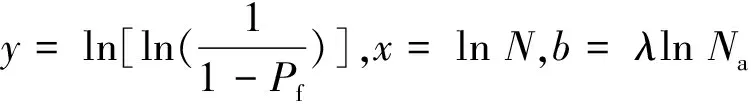
y=λx-b

(4)

式(4)为直线方程，Weibull分布的参数λ和b均可由图解法线性拟合得出。式(4)可以用来检验同一应力水平下的疲劳寿命值是否符合两参数Weibull分布。不同应力水平下NAC和RAC的疲劳寿命Weibull分布如图4所示。

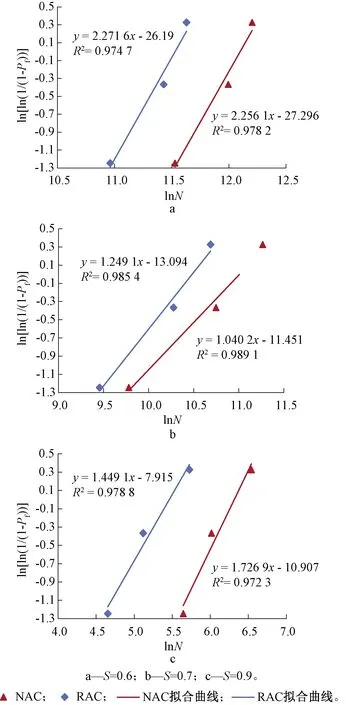
图4 NAC和RAC疲劳寿命Weibull分布检验

由图4可以看出，y与x在不同应力水平下均存在线性关系，且相关系数R2均超过0.90且接近于1，可知用两参数Weibull分布来描述NAC和RAC的疲劳寿命是较为可靠的。

图5为NAC和RAC的形状参数，形状参数值越大，混凝土疲劳寿命离散性越小[18]。NAC和RAC的形状参数随着应力水平的增大，均呈先减小后增大的趋势，在应力水平为0.7时两者形状参数都达到最小值，也就是说，应力水平为0.7时，NAC和RAC的疲劳寿命离散性最大，且NAC较RAC离散性更为明显。当应力水平较小(应力水平在0.8以下)时，NAC的疲劳寿命离散性较RAC大，随着应力水平增大，NAC的疲劳寿命离散性较RAC小，说明NAC在高应力水平下疲劳寿命的分布较RAC更均匀，离散性更小，抗弯曲能力较好。

图5 NAC和RAC的形状参数

2.4 考虑失效概率的S-N-Pf方程

由式(1)可知疲劳寿命的计算式：

N=Na|ln(1-Pf)|1/λ

(5)

由式(5)可得到NAC和RAC在不同失效概率下的疲劳寿命。实际工程中往往需要根据失效概率建立S-N-Pf方程，本文采用双对数疲劳方程(6)来进行疲劳分析[12]。

lgS=β-αlgN

(6)

式中：α、β为回归参数。

根据式(6)，将数据进行图解法拟合可得到图6所示NAC和RAC在不同失效概率下弯曲疲劳曲线，回归结果和弯曲疲劳方程如表4所示。

图6 不同失效概率下NAC和RAC的S-N-Pf曲线

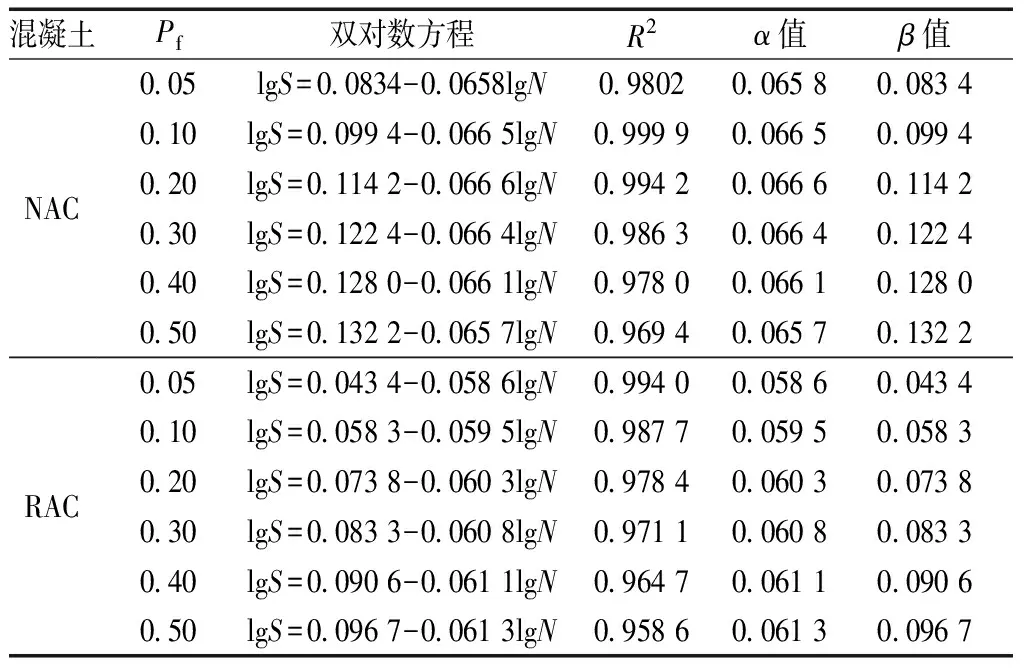
表4 不同失效概率下的双对数疲劳方程

由图6和表4可知，不同失效概率下相关系数R2均大于0.9且接近于1，说明式(5)中lgS和lgN存在良好的线性关系，可知S-N-Pf方程可以很好地描述表示应力水平与疲劳寿命之间的关系。在同一应力水平下，失效概率越大，即存活率要求越小时，混凝土弯曲疲劳寿命越大。在疲劳寿命相同时，应力水平越高，失效概率也相对越大。

当失效概率Pf为0.1、0.2、0.3、0.4、0.5时，NAC的疲劳方程中的回归参数α值较失效概率Pf为0.05时分别提高了1.06%、1.22%、0.91%、0.46%、-0.15%，回归参数β值较失效概率Pf为0.05时分别提高了19.18%、36.93%、46.76%、53.48%、58.51%。RAC的疲劳方程中α值较失效概率Pf为0.05时分别提高了1.54%、2.90%、3.75%、4.27%、4.61%，β值分别提高了34.33%、70.05%、91.94%、108.76%、122.81%。且当失效概率改变时，RAC的α值和β值均小于NAC，可知NAC在不同失效概率下抗弯疲劳性能均比RAC好，RAC较NAC来说，在不同失效概率下的弯曲疲劳寿命对循环应力水平变化更敏感。

3 疲劳可靠度分析及寿命预测

3.1 基于Palmgren Miner疲劳模型的可靠度分析

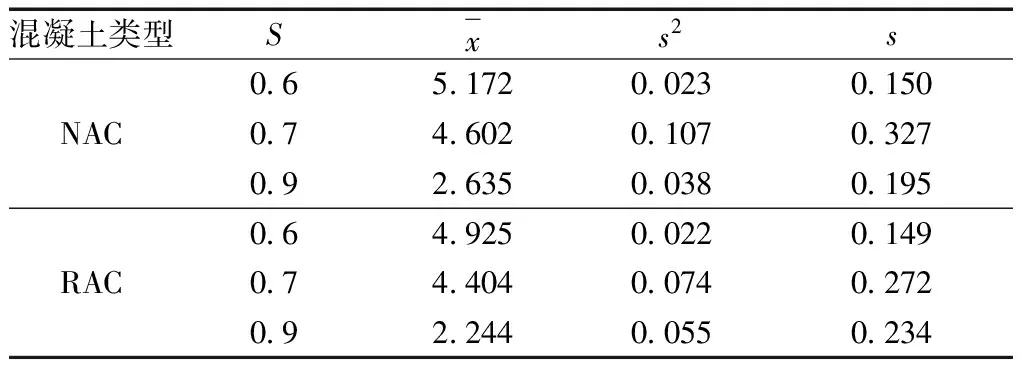
表5 疲劳试验结果统计分析

随机变量疲劳损伤D=n/N的概率密度函数为：

(7)

式中：μ和σ分别为疲劳寿命的平均值和标准差；n为荷载循环次数。

将表5中数据代入式(7)，可得出应力水平分别为0.60、0.70、0.90时的概率密度函数方程见式(8)。

(8)

式中：ai、bi、ci为系数，其值如表6所示。

表6 概率密度函数q(D)中的系数

经大量试验证实，多数材料损伤变量D的临界值并不会达到1，而是分布在[0.2,0.8]区间内，故对式(8)中D在区间[0,0.5]上进行积分[19]。所得疲劳可靠度结果如图7所示。可见，NAC和RAC的疲劳可靠度均从100%下降到0，无论应力水平如何，NAC在相同循环次数下，疲劳可靠度均大于RAC。随着应力水平的升高，NAC和RAC的疲劳可靠度均相应降低。

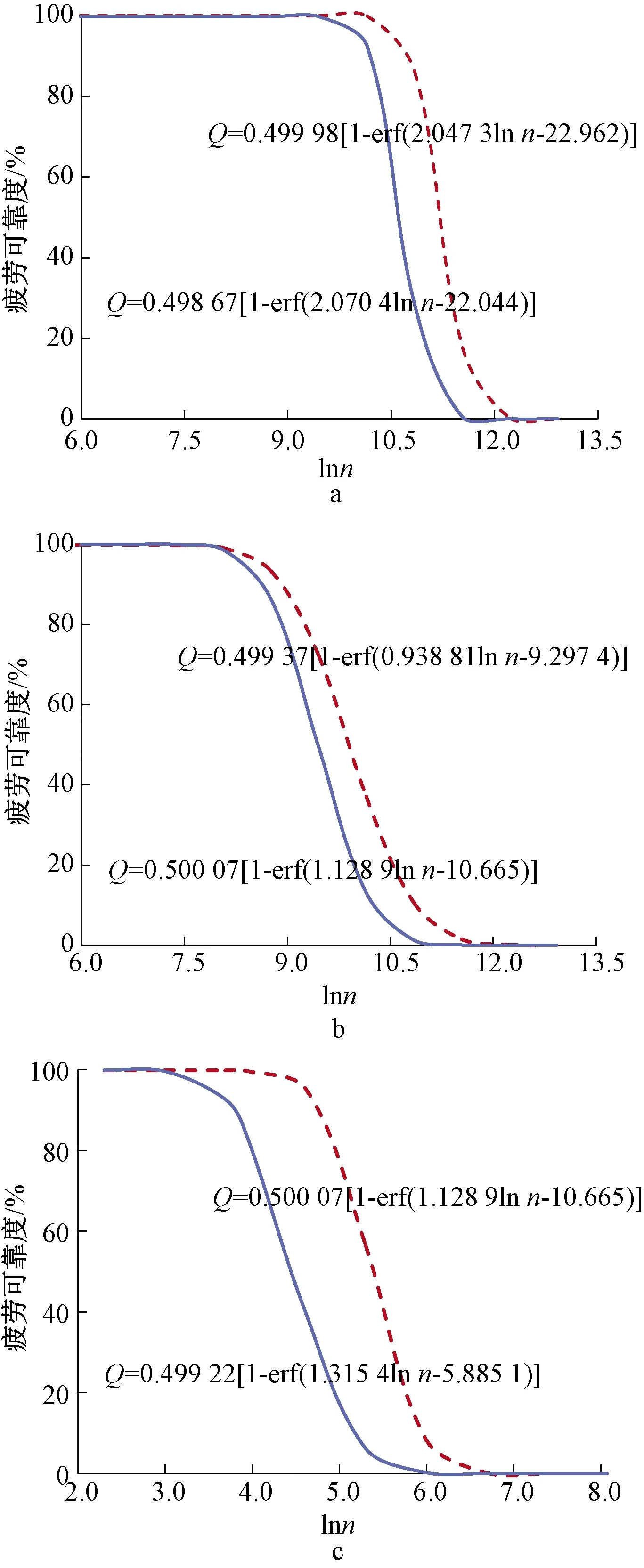
a—S=0.6；b—S=0.7；c—S=0.9。

3.2 不同可靠度下的疲劳寿命预测

由式(5)及图7中可靠度计算式可得出不同失效概率对应的预测疲劳寿命，计算结果见表7，为了更直观比较两种情况下再生混凝土预测疲劳寿命值，将表7中数据绘制于图8。可见，在对NAC的疲劳分析中，假设循环次数遵循Weibull分布和对数正态分布所得出的不同可靠度下的疲劳寿命区别较大，且使用Weibull分布较对数正态分布所得出的疲劳寿命更为接近临界值，在对RAC的疲劳分析中，假设循环次数遵循Weibull分布和对数正态分布所得出的不同可靠度下的疲劳寿命相差不大，使用对数正态分布比Weibull分布得出的疲劳寿命更为接近临界值。由于在对RAC的分析中，离散性较大，使得Weibull分布数据较不稳定，而使用对数正态分布对不稳定数据的处理更好。

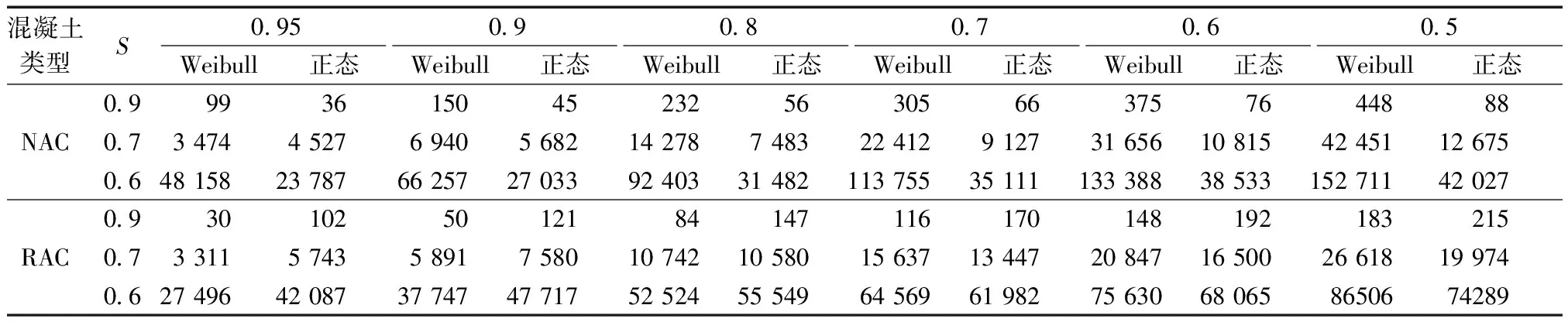
表7 不同可靠度Q下的预测疲劳寿命N

a—AC；b—RAC。

4 结束语

1)在同一应力水平下，RAC在循环荷载作用相同次数时的纵向应变大于NAC的纵向应变。

2)NAC和RAC的弯曲疲劳寿命均能较好服从两参数Weibull分布，其疲劳寿命的离散性均随着应力水平的增大先增大后减小。

3)根据试验结果，运用图解法得出了应力水平和疲劳寿命的双对数S-N-Pf方程。

4)对NAC的分析中，假设疲劳寿命N服从对数正态分布和Weibull分布所得出的不同可靠度对应的疲劳寿命相差较大，Weibull分布所得值更接近临界值。对RAC的分析中，假设疲劳寿命N服从对数正态分布和Weibull分布所得出的不同可靠度对应的疲劳寿命相差不大。