虚假数据注入攻击下线性系统的非模型预测控制*

张泽禹，李宏然

(江苏海洋大学 计算机工程学院，江苏 连云港 222005)

0 引言

网络化是现代化中最重要的组成部分之一。随着互联网技术的推广与更新，各领域逐步引入无线通信技术，如海洋开发与探索、能源互联网、智能电网等。海洋是至今仍未被全面了解的领域，人类对海洋的开发与探索从未停止。随着海洋开发技术的不断进步，勘探设备将数据传输方式从有线转为无线的需求与日俱增[1]。然而，无线通信技术在带来极大便利的同时也带来诸多安全隐患。连接方式由有线变为WiFi、蓝牙、红外等无线技术，使得攻击者能够更容易连接到控制系统中进行破坏[2]。对此，研究人员开发了各种防御策略防止攻击造成不良影响[3]，如攻击检测器、拥有不确定性的系统、数据过滤器等。

2009年的“震网”事件令伊朗核设施停运，也让德黑兰核计划推迟数年。同时，全球几乎所有领域甚至海洋勘探船舶的计算机中都检测到了“震网”病毒[4]。“震网”病毒开启了隐蔽性攻击的新阶段。黑客制作出的恶意攻击方式不再能够被及时发现，当人们意识到设备在非正常运行时，系统已被入侵很久且受到了不可逆损坏。电网系统的结构复杂且容易产生漏洞，攻击者极易利用这些漏洞进行虚假数据注入攻击[5]。此类攻击的目标是将有害数据注入到系统的原始数据中破坏硬件设备[6]。目前，不同类型的安全问题逐渐在海洋及船舶领域被发现，这无疑会给海洋探索带来困难[7]。

虚假数据注入攻击属于隐蔽性数据类攻击，攻击者通过漏洞进入控制系统，篡改状态估计结果，致使系统崩溃、设备停转或损毁，具有极大的危害。针对此种攻击方式，文献[5]验证了互感器的配置冗余度及合理性在防御攻击方面的重要性，从而以此为基础制定量测保护策略。文献[8]开发了基于Bi-GRU和自注意力的检测器，将准确率和正报率分别提升了7.1%和3.95%，同时使误报率平均降低38.85%。文献[9]设计了积分滑模控制来稳定直流微电网的母线电压，阻止虚假数据注入攻击对电网系统的破坏。文献[10]通过对比容积卡尔曼滤波算法和加权最小二乘法的估计结果来检测是否有攻击产生，若两种状态估计结果差距较大，则说明系统受到攻击。文献[11]通过分析直流微电网的暂态扰动过程判断是否存在虚假数据注入攻击，通过改变数据权重来降低攻击的损害。上述研究均从不同角度和情况出发制定应对虚假数据注入攻击的防御策略。但当这些方法在某些情况下失效时，系统则不能及时作出应对。

一些研究者也注意到了这些防御策略失效时的缺点。例如，文献[12]提出了针对拓扑信息不完整、融合胶囊网络和物理网络模型的自适应窗口共三种不同情况下的防御策略。文献[13]提出了结合遗传算法和混合整数规划模型并使用遍历的方式求解，防御虚假数据注入攻击。文献[14]使用卡尔曼滤波器对文中设计的输出跟踪控制系统的原始数据进行过滤。以上方法也更具有一般性，但还是要为系统设计额外的安全装置，无法从根源处应对虚假数据注入攻击。

海洋勘探作业主要使用水下机器人作为行动载体，而水下机器人的控制系统为线性控制系统[15]。因此，本文将线性系统的非模型预测控制作为研究基础[16]。非模型预测控制可以摆脱实际应用中系统模型的束缚，更具有普适性[17]。多项式回归方法[18-19]能够构造不同数据间的关联，使数据具有相似的特性。本文创新点在于对线性系统使用非模型预测控制，并在此基础上应用多项式回归方法，将恶意攻击数据归类为另一个可用数据集。这样，虚假数据注入攻击的数据峰值将会被构造的数据关联削弱，从而维持系统稳定运行，达到防御虚假数据注入攻击的目的。

本文首先介绍非模型预测控制的基础原理，阐述预测控制数据求解方法，然后介绍攻击数据注入控制系统后的求解原理，最后通过仿真实验证明本文理论的有效性。

1 线性系统的非模型预测控制

水下机器人的系统模型可以用雅可比矩阵线性化，系统模型为

y(t+1)=β1y(t)+β2u(t)+β3u(t-1)。

(1)

其中，βi(i=1,2,3)为常量参数。若为系统应用非模型预测控制，式(1)可转化为

y(t)=f(x0(t))。

(2)

y(t)为不受高斯白噪声影响的线性函数形式。

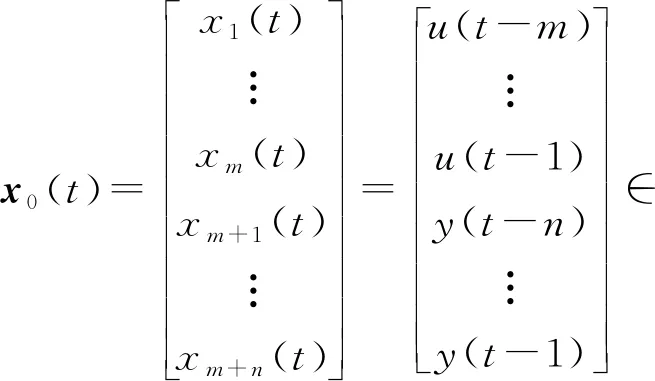
(3)

x0(t)是系统状态向量，由不同时刻输入数据和输出数据构成，m和n是系统状态数量参数，代表系统状态总维度。控制系统预测目标是令未来d个时刻的输出轨迹

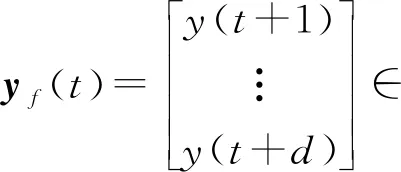
(4)

贴合于参考轨迹

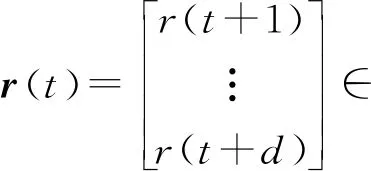
(5)

其中，d是将要预测的总步数，而d个时刻的预测输入为

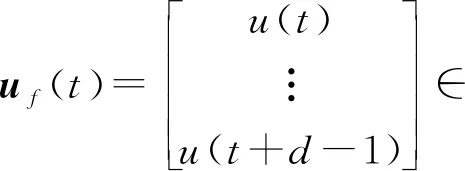
(6)

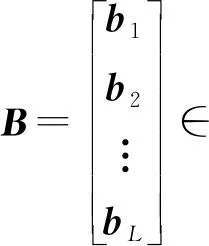
将N组历史输入数据up(tl)和输出数据yp(tl)(l=1,2,…,N)构造成的向量为

(7)

cl=uf(tl)∈d。

(8)

其中，

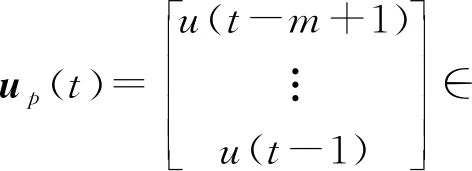
(9)

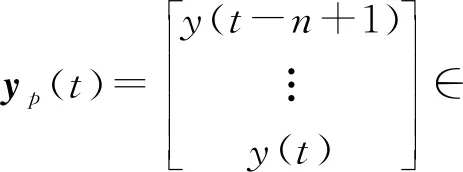
(10)

为了计算系统d个时刻的预测输入向量uf(t)，将历史输入向量up(t)、历史输出向量yp(t)和参考轨迹向量r(t)构造成目标向量

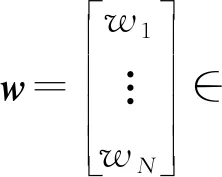
(11)

联合求解最优目标设置为

Aw=b,

(12)

uf(t)=Cw。

(13)

其中，

(14)

(15)

(16)

通过L2范式求解最优向量w：

min||w||2subject toAw=b。

(17)

联立式(11)和式(12)可解得最终预测目标uf。

2 多项式回归

对于现实应用中的控制系统，输入数据维度并不总能匹配系统矩阵的维度。为了获得更多系统状态数据，可以使用伪张量将状态向量扩展为多项式。当l>1时，对al和b使用伪张量扩展为多项式

(18)

(19)

伪张量运算具体原理公式为

(20)

而张量运算公式为

(21)

可以看出，两种运算的不同之处是伪张量只保留张量运算结果中的一个相同分量，使分量满足张量不变性定义。此后，控制系统状态向量维度满足运行所需数量，系统矩阵重新定义为

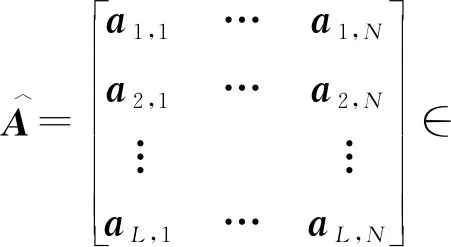
(22)

(23)

然后，使用多项式来应对注入到系统中的虚假数据。可以将虚假数据注入攻击数据视为额外输入数据，只需调整数据数值大小就可以补充原始数据维度空缺。例如，受到攻击后，使用多项式回归可以将式(18)和式(20)改为

(24)

(25)

同理，将Z和B替换式(12)中的A和b后联立可解得最优的预测目标uf。

3 仿真实验

本文设计了一个水下机器人的线性控制系统仿真实验来证明本文理论的有效性[15]。首先，系统模型设置为

y(t+1)=0.7y(t)+0.4u(t)+0.06u(t-1)+e1(t)。

(26)

其中，e1(t)是为符合实际应用情况而设置的高斯白噪声。

系统的参考轨迹设置为

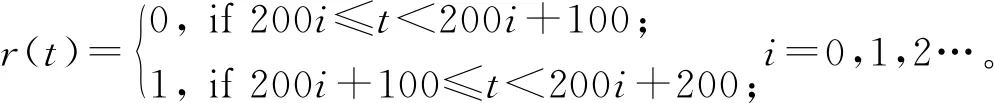
(27)

线性系统在未被攻击时的原始数据如图1所示，数据的数值分布如图2所示。此数据集由仿真随机产生，这样的数据集符合实际应用，同时也更具有一般性，适用于大多数场景。

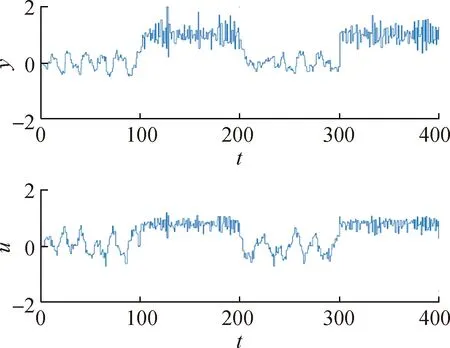
图1 正常情况下的系统数据

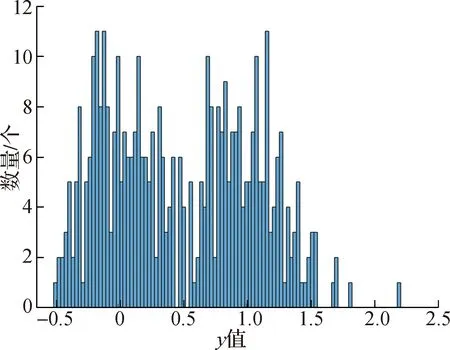
图2 正常情况下的系统数据分布

系统未受到攻击时预测控制仿真结果如图3所示，上方为系统预测输出数据，下方为预测输出数据与参考轨迹之差。可以看出，输出轨迹基本贴合参考轨迹，两者差值较小。

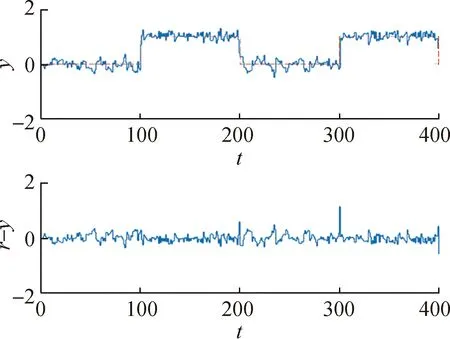
图3 正常情况下的仿真结果

系统未受到攻击时的箱型图如图4所示，该图能够反映系统的精确性，图中蓝色矩形的高度越小系统越可靠。图中矩形高度区间约为(-0.1，0.1)。

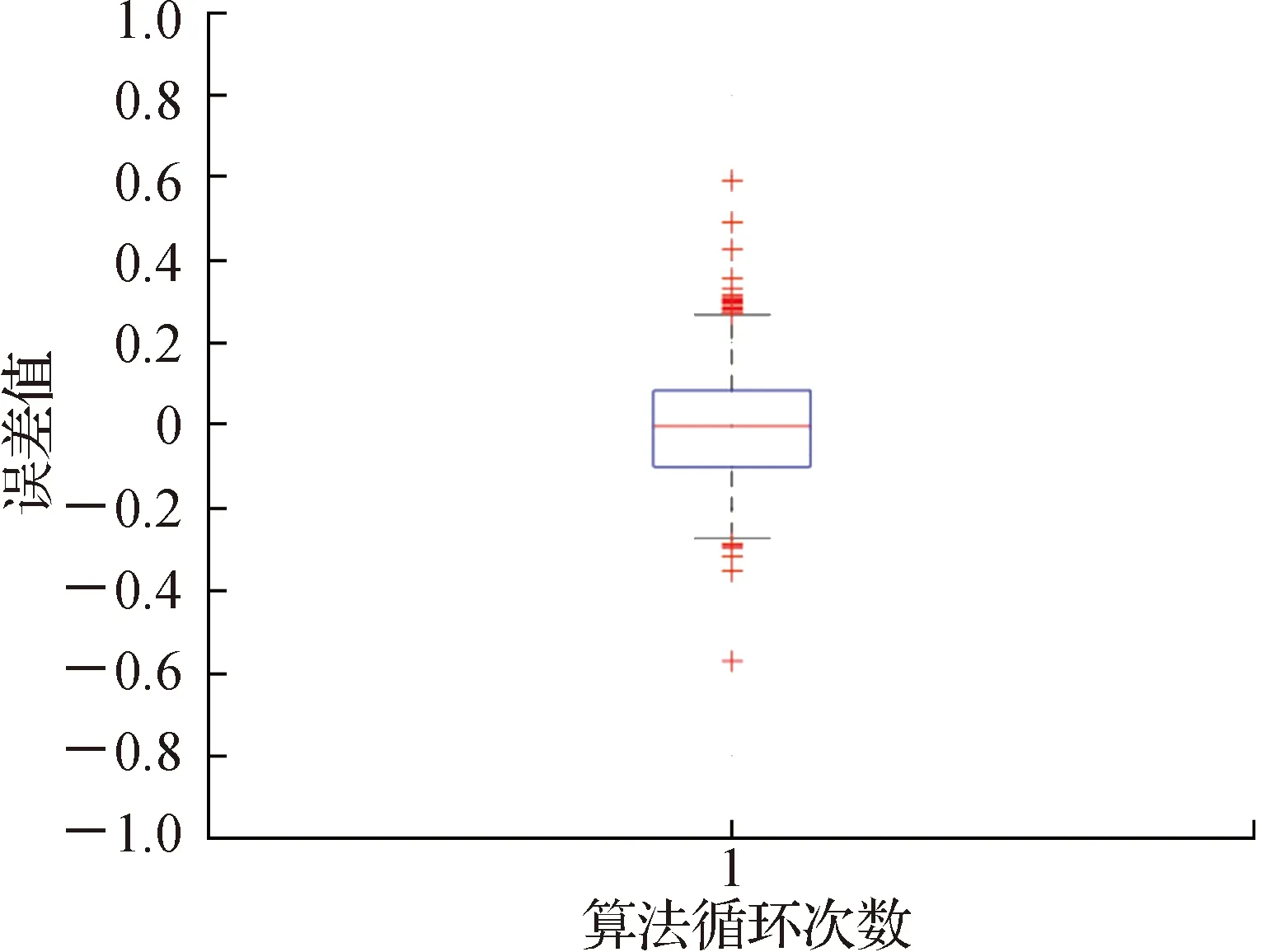
图4 正常情况下的箱型图

使用多项式回归的非模型预测控制系统在受到虚假数据注入攻击后的数据集如图5所示，数据集分布情况如图6所示，数据集仍为随机生成。对比图1和图5可以看出，攻击后数据波动更小，这是虚假数据注入攻击隐蔽性的表现。

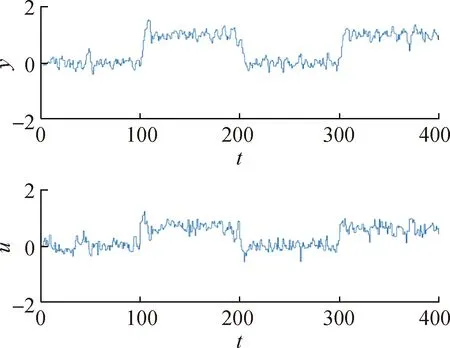
图5 被攻击后的系统数据

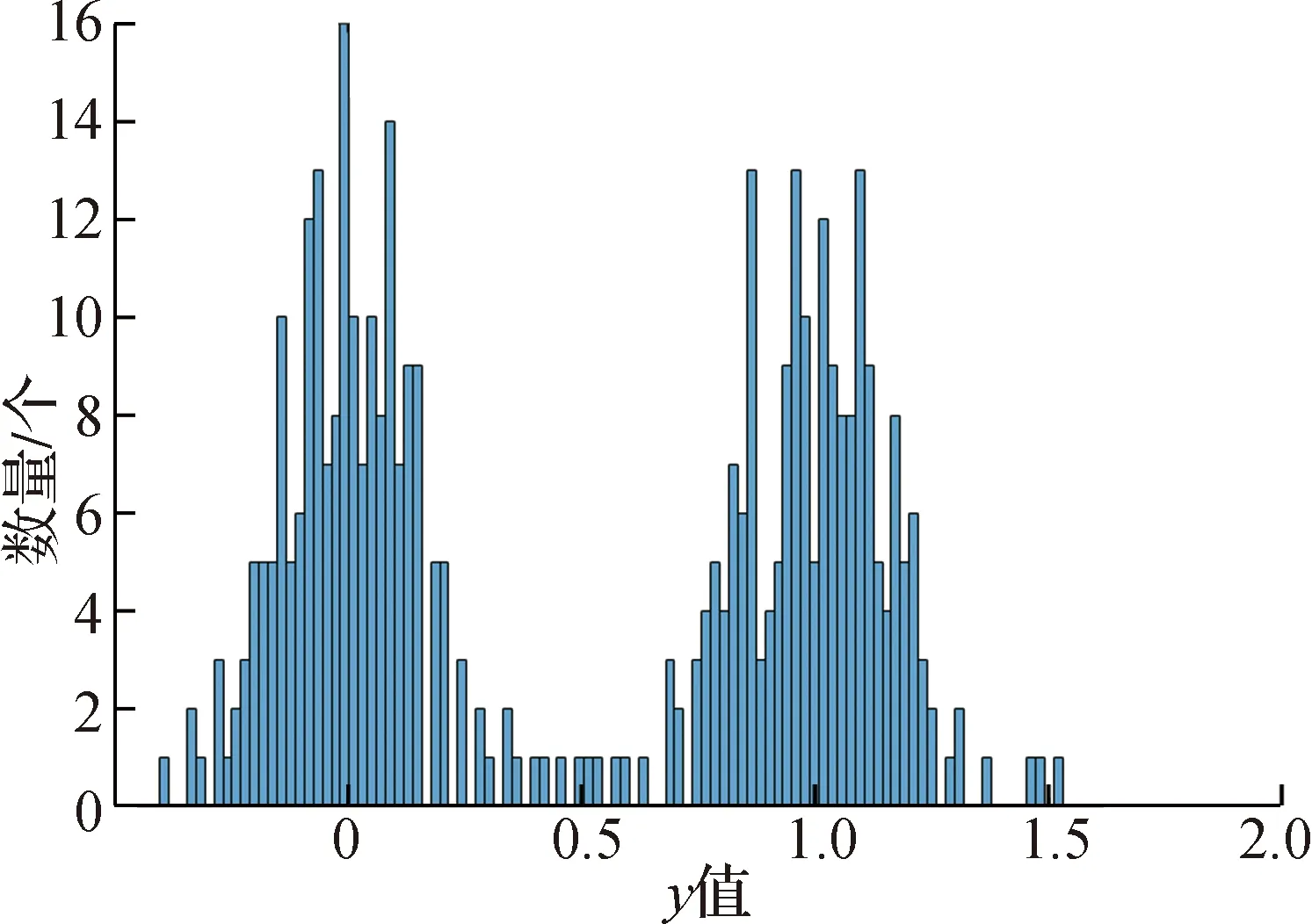
图6 被攻击后的系统数据分布

使用多项式回归的系统在受到攻击后预测仿真结果如图7所示。对比图3和图7中输出轨迹与参考轨迹之差可以看出，图7中的差值较大，这是系统关联了攻击数据后的结果。

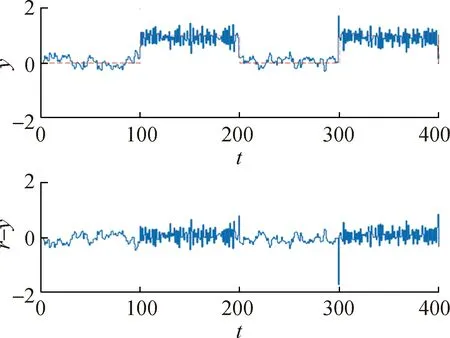
图7 FDI攻击后无模型预测控制系统的仿真结果

被攻击后多项式回归系统的箱型图如图8所示，图中的蓝色矩形高度区间约为(-0.2，0.2)。对比图4和图8可以看出，受到攻击后系统精度较低，而使用了多项式回归的系统在受到攻击后依然能够稳定运行，这也表明该方法在保护控制系统乃至设备完整性方面效果较好。

图8 被攻击后无模型预测控制系统的箱型图

4 结论

为了消除虚假数据注入攻击带来的威胁，本文提出了采用关联数据的方式削弱攻击强度。不同于常规检测或过滤等机制，该方法能在基础数据层面防止系统崩溃，保护设备完整性。然而，由于攻击数据的数值过大，即使使用多项式构造数据间关联，也无法完全消除攻击影响。本文所提出的方法以小部分系统精度的损失维持了系统稳定性。多项式回归的方法在非线性系统上能否得到应用将作为未来的一个研究方向。