基于改进弗洛伊德算法的救护车应急救援路径规划*
李 慧,王晨曦,贾东宝,韩国凯,侯鹏飞,邢立豹,顾 勇
(江苏海洋大学 计算机工程学院,江苏 连云港 222005)
随着我国工业发展的深入和工业生产规模的扩大,包括火灾在内的各类工业突发事故数量不断增加,造成了严重的人员伤亡和财产损失。如何根据事故发生的实际情况,规划出最佳的应急救援路径,用最少的时间展开应急救援,减少人员伤亡,减轻财产损失,已经成为相关领域的研究重点。
目前,主流的救护车调度算法可以分为三类。第一类是基于交通道路的拥挤情况对急救车辆进行实时调度,如文献[1]提出的根据车辆行驶时间,综合考虑道路拥堵情况,实现救护车辆实时调度的方法;文献[2]在救护车运行控制过程中根据道路拥堵的情况动态对救护车进行调度。虽然这些调度方法考虑到了道路拥堵情况,但却忽略了患者和救护车的地理位置、车辆使用情况及医院救援物资情况等。第二类是基于遗传算法对救护车调度进行优化,如文献[3]使用遗传算法对救护车部署和调度问题进行了优化,旨在最大限度地提高患者的预期存活概率;文献[4]提出了基于遗传算法的优化框架,使用了响应时间最小化、覆盖范围最大化的最近调度规则。第三类方法是对急救车辆在调度前实施一些预评估方案,如文献[5]将生存功能纳入调试方案,根据患者的类别预先建模,从而对救护车辆进行分配;文献[6]提出为满足对救援物资的需求,同时考虑到每个需求的紧迫性,为每个节点设置优先级,按照优先级大小依次提供救援。虽然这些调度考虑到了医疗物资情况、病人救治率等因素,但未考虑调试过程中交通道路的拥堵情况,不利于救护车的实时调度。
本文采用改进的弗洛伊德算法,综合考虑道路拥堵情况、医院救援物资情况、患者和医院地理位置以及车辆空闲情况等重要因素,对不同路径动态赋予不同权值,得到一个综合权值,以此规划出最优的救护路径,从而实现对急救车辆的智能调度。
1 问题定义
救护车路径选择的目的是为实施救助的医护人员规划一条最佳路径,以确保救护车辆能够快速到达现场实施救援。规划最优路径需要找到任意两个地点之间的最短路径,同时还要考虑道路拥堵状况、医院救援物资情况和车辆空闲情况,以及患者和医院的地理位置信息等一系列因素,以此得到路径选择的最优解。
为了评估所得解的优劣,本文将救护车和被救治病人之间的权值作为目标函数值。救护车路径搜索问题建模如下:
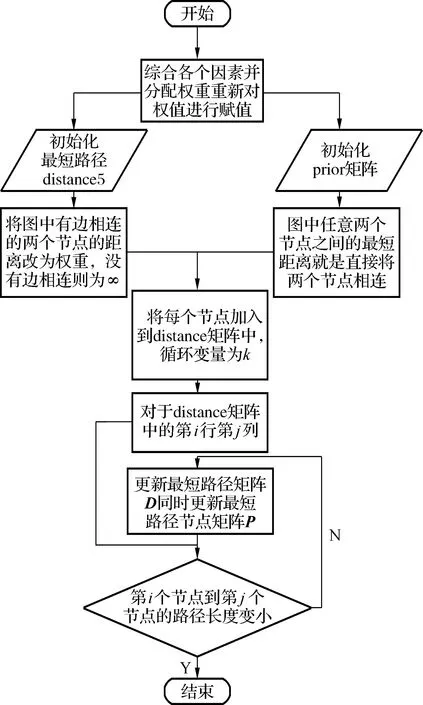
W=(d[i][j]+h×ri+g×ri)×s;
(1)
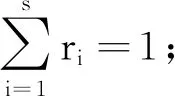
(2)
Q=(q1,q2,q3,…,qf),f≥0;
(3)
M=(m1,m2,m3,…,mt),t≥0。
(4)
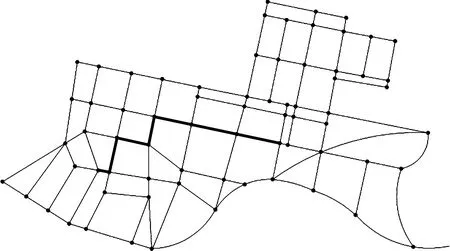
目标函数(1)表示在紧急调度的过程中救护车和病人之间的权值,其值越大,所选路径耗时越长;式(2)中R表示所有权值因素占比集合,且占比之和为1,用P矩阵来存储医院和患者之间的路径信息,用D矩阵来存储医院和患者之间的最短路径距离;式(3)中的Q表示道路拥堵情况集合;式(4)中M表示医院的救援物资情况。本文根据CAD软件绘制交通路线图,通过ArcGIS的网络数据集工具ArcMap在每一个交叉路口进行打断处理,建立如图1所示的交通网络模型[7],然后将交叉点抽象为结点,路段抽象为边,最终得到如图2所示的路径结点网络。
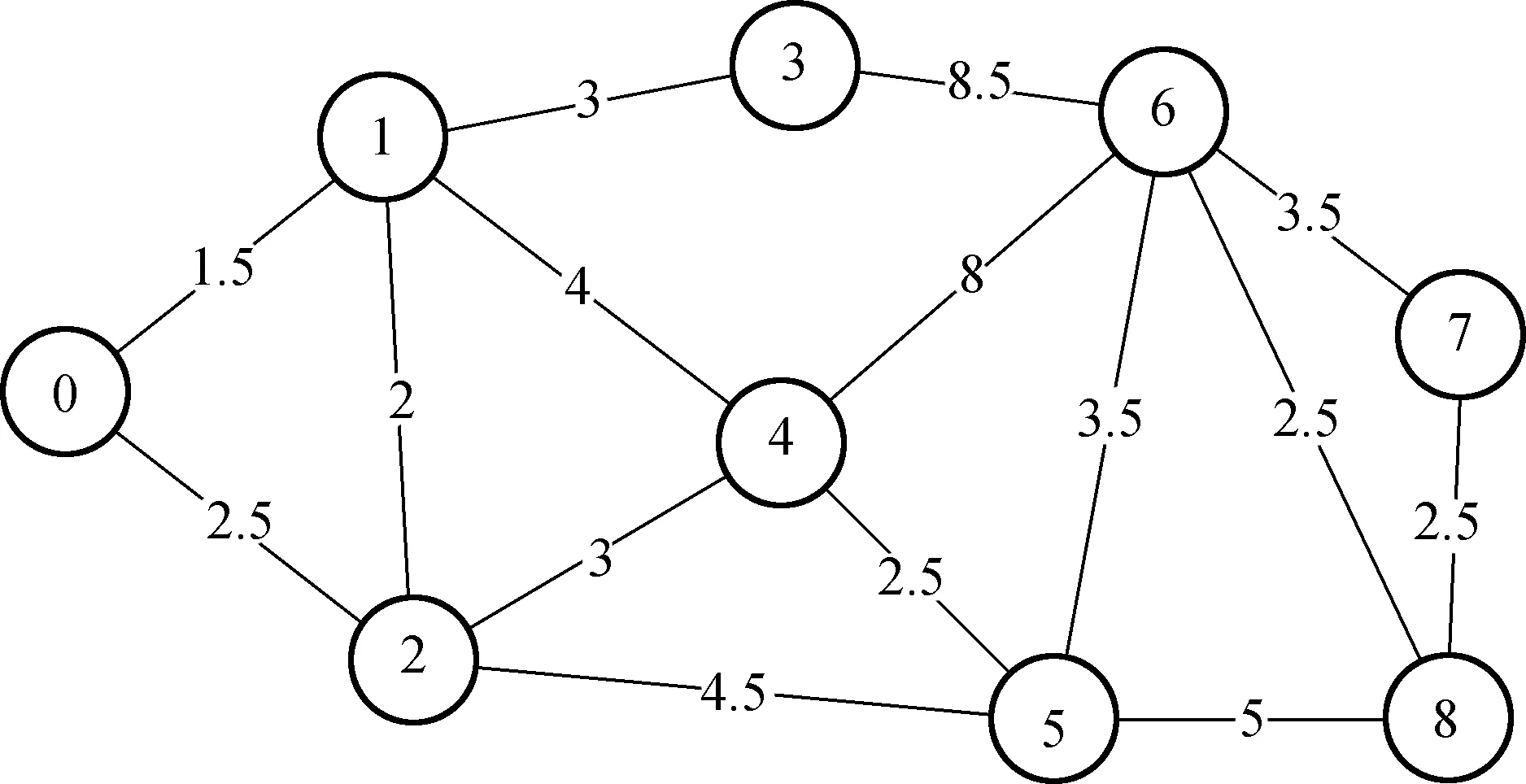
图1 交通道路网络模型
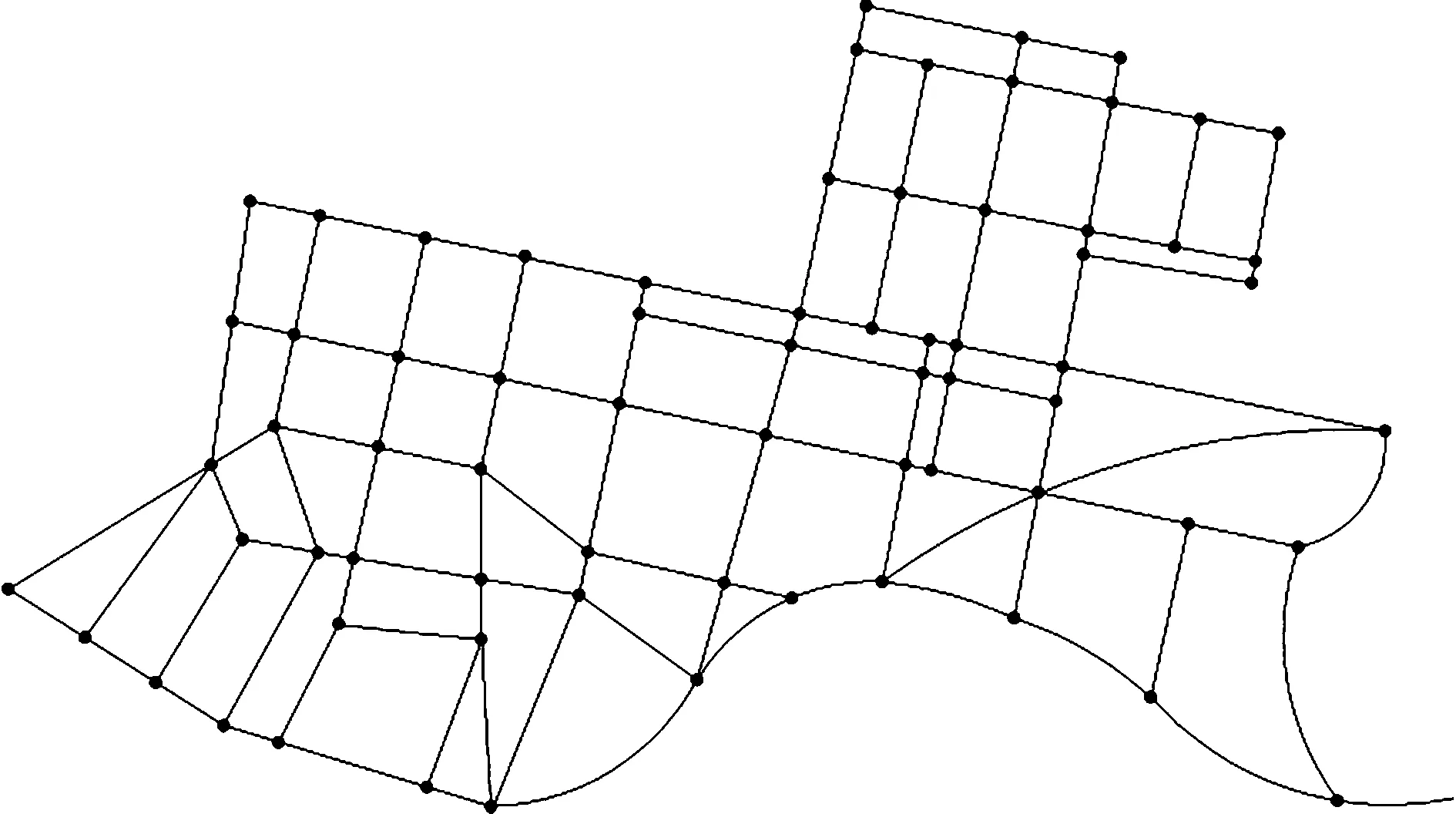
图2 路径结点网络
道路网络模型可用式(5)表示[8]:
(5)
式中:RM表示交通道路网的模型;M表示在交通道路网中各个顶点的集合;R表示道路网中具体路径的集合,其元素为有序对(e,f),(e,f)表示顶点e与顶点f之间有向连通,lef表示顶点e与顶点f之间的加权路径长度[9];LV表示道路网中连通两点之间的加权路径长度集合。路径的加权长度仅仅是两个顶点之间的距离。
2 传统弗洛伊德算法
2.1 弗洛伊德算法描述
弗洛伊德算法是用来求加权图之间的各个多源顶点之间最短路径的算法,添加或减少任意顶点,它都可以动态地实现最短路径规划。该算法以1978年图灵奖获得者罗伯特·弗洛伊德命名[10]。
弗洛伊德算法的主要思想为:将所有的结点和边都放在图中进行表示,图中的权值表示两个结点之间的距离,两个顶点之间不直接可达的距离用无穷来表示,将图中的信息转化成邻接矩阵的形式,每加入一个新的结点即更新邻接矩阵的路径长度,通过中间结点就可以求出任意两个结点的最短路径,新生成的路径会储存在路径矩阵P中。
2.2 弗洛伊德算法实现步骤
首先对各条边之间的权值进行初始化。定义一个矩阵P用来记录所插入点的信息,定义D矩阵用来记录顶点之间的路径长度信息。在D矩阵中,如果两个顶点之间没有直接连通的路径,记D[i][j]=无穷大,如果两个顶点之间可达,则D[i][j]=d。对于图中的任意一对顶点x和y,判断是否存在一个顶点z,使得从x经过z到y比已知的路径更短,如果存在,那么就更新P矩阵。初始化P[i][j]=j,把各个顶点V插入图中,比较插点后的距离与原来的距离,D[i][j]=min(D[i][j],D[i][k]+D[k][j]),如果D[i][j]的值变小,P[i][j]=k。例如,要寻找从V6到V2的路径,根据P,假如P(6,2)=4,则说明从V6到V2经过V4,路径为{V6,V4,V2};如果P(6,3)=3,说明V6与V3直接相连;如果P(6,1)=1,说明V6与V1直接相连。
由上述分析可知,任意加入一个新的节点,通过弗洛伊德算法都可以求得任意两个顶点之间的最短路径。
弗洛伊德算法可用下面伪代码表示:
Void Floyd()
{
int s,t,h;
for(h=1;h<=n;h++)
for(s=1;s<=n;s++)
for(t=1;t<=n;t++) if(dist[s][h]+dist[h][t] dist[s][t]= dist[s][h]+dist[h][t] } 传统的弗洛伊德算法虽然可以用来进行最短路径规划,但是它仅仅考虑了路径的长度而忽略了道路拥挤情况、救援物资情况、车辆空闲情况等其他因素对结点之间权值的影响,所以需要在传统弗洛伊德算法的基础上进行优化。 对式(5)中的lef进行优化并重新对权值进行赋值,将各个因素都纳入到权值的占比中,对每个部分的占比进行灵活分配,将各个因素进行加权求和之后得到一个新的权值,然后再采用弗洛伊德最短路径算法规划出一条最佳的路径。改进后的算法流程如图3所示。 图3 改进后弗洛伊德算法流程 第一步,为了对弗洛伊德算法进行进一步优化,将所有的信息进行初始化。首先将整个医院地图信息优化成完全带权图G,将医院设为节点v0,然后在患者求救时将患者的节点v1,v2,…,vn加入到集合V中。 第二步,对医院与患者之间的路径权值进行动态规划。首先通过地图测出医院与患者或者患者与患者之间的实际路径长度,即图中各个顶点之间的实际距离di。其次对每个因素划分为11个等级。例如,道路拥堵情况划分为0~10共11个等级,根据实际道路情况确定等级,道路拥堵时可以取值为9或10,道路畅通时可以取值为0或1。 为了便于理解,本文仅考虑道路的拥堵情况和医院的物资情况两个因素,对道路拥堵情况的评级用h表示,对医疗物资的情况评级用g表示。根据W=(d[i][j]+h×ri+g×ri)×s计算出权值。 第三步,引入AK(i,j),表示从i到j的途中不经过索引比k大的最短路径,然后用最短路径计算公式 AK(i,j)=min{AK-1(i,j),AK-1(i,k)+AK-1(k,j)} 计算出AK(i,j),当K=n时(n为索引的总个数),An(i,j)=D[i][j],即可求出经过多种因素下的最短路径。并令P[i][j]=k,将经过的最短路径节点加入到集合p中。 采用了改进弗洛伊德算法后,对各个结点的权值进行重新赋值可以更加实际地实现对急救车辆的调度。 本文采用 CAD,Visual Studio,ArcMap,IDEA等工具开发了救护车智能调度软件。选取连云港市的交通道路网络作为研究数据,将各种交通路口、市区主干道等要素添加到数据库中,并通过CAD的图形绘制工具得到如图4所示的连云港交通路线图。 图4 连云港交通路线图 以下是一个弗洛伊德算法实例。 (1) 将起点V0加入到Path[]数组中得到新的Dist[]矩阵(a)和Path[]矩阵(b)。 b Path[]矩阵 (2) 起点V1加入到Path[]数组中,得到新的Dist[]矩阵(c) 和Path[]矩阵(d) 。 d Path[]矩阵 c Dist[]矩阵 (3) 以此类推,当起点V8加入到Path[]数组中时算法结束。此时得到新的Dist[]矩阵(e)和Path[]矩阵(f)。 a Dist[]矩阵 f Path[]矩阵 (4) 根据距离矩阵和路径矩阵可得到任意两点间的最短距离。例如从V4→V7的最短路径,从P矩阵可得最短路径为V4→V6→V7。综合考虑各个因素的影响,重新对权值进行赋值。 对每个可能因素都赋予不同的比例,计算出最合理的权值,此时得到的结果和路径更为准确,能高效地运用在救护车的智能调度中。将传统的Dijkstra算法嵌入到软件中,规划出了如图5所示的应急救护车最短路径(图中加粗线段)。 图5 弗洛伊德算法下的最短路径 本文对道路拥堵情况、救援物资情况、车辆空闲情况以及患者和医院的地理位置等进行综合考虑后,将改进的弗洛伊德算法嵌入到软件中,重新规划出了如图6所示的最短路径(图中加粗线段)。 图6 改进弗洛伊德算法下的最短路径 假设车辆匀速行驶,经过一个交叉路口平均等待30 s。图5的路径长度为1 508.6 m,经过11个交叉路口,用时15.6 min。图6的路线长1 709.8 m,经过8个交叉路口,用时13.5 min。图6路线在实际运行过程中有效地避开了拥堵路段,且综合考虑了患者求救的地理位置信息,虽然其路径比图5规划路径更长,但用时更少,救治效率更高。 采用文献[11]网络拓扑结构(网络节点数取8),将弗洛伊德算法和改进的弗洛伊德算法进行比较,以验证所提算法的有效性。实验在Matlab 2016b上对每种算法求得的最优解进行多次仿真测试。弗洛伊德算法不考虑其他因素的影响,故路径权重因子赋值为0,而改进的弗洛伊德算法考虑其他因素的影响,故路径权重因子赋值为1。不同路径权重因子的网络结构如图7和图8所示。 图7 路径权重因子为0的网络结构 图8 路径权重因子为1的网络结构 由图7可知,当路径权重因子为0时,此时未考虑其他因素的影响,可认为是采用弗洛伊德算法求得起点到终点的最短距离(即图中加粗线段),图中权值仅代表由各路径间距离计算出的权值。当路径权重为1时,结合式(2)和式(3),综合考虑道路拥堵情况、医院救援物资情况、患者和医院地理位置、车辆空闲情况等,对权值公式进行计算得到如图8所示的网络结构。此时的权值代表综合各因素后的地点之间的路径长度,此时再采用弗洛伊德算法求得从起点到终点的最短路径(即图8中加粗线段)。 下面通过仿真模拟环境1(路径权重因子为0)和模拟环境2(路径权重因子为1)的实验结果(见表1),来具体比较两种算法在救护车智能调度中的效率(车辆运行速度取80 km/h)。 表1 模拟环境下的实验结果 比较发现,当权重因子为0时,起点到终点的距离由最短路径长度决定,此时最短路径经过的结点为0→1→3→6→8,由弗洛伊德算法计算可得用时为16.5 min。但实测用时为22.0 min,表明算法的局限性极大地影响了急救车辆的调度效率。当权重因子为1时,综合考虑道路拥挤、救援物资、患者和医院地理位置、车辆空闲等因素影响,得到最短路径为0→2→5→8,所用最短时间为21.5 min,实测用时22.0 min。可以看出,采用改进的弗洛伊德算法效率较高,与实际用时相差仅为2.27%。 为了验证改进弗洛伊德算法的通用性和有效性,本文采用salam网络拓扑随机生成算法生成10~45个节点的对称网络结构,将网络结点数量扩大并随机生成。仿真实验不仅可以验证本文算法的正确性,还可以扩展到较大的网络结构[12-13]。 在此基础上,本文定义路由优化失败率,它表示在运行算法时找不到最短调度时间的次数占总次数的百分比。一般认为,路径失败的相对频率接近于所计算的路径不是最短调度时间的概率。每种节点数情况下随机生成20种网络拓扑结构,对应每种网络拓扑结构各算法均运行50次节点数,失败率取平均值[12]。 图9表示不同节点数下改进弗洛伊德算法与经典弗洛伊德算法的优化失败率对比情况。改进弗洛伊德算法的计算优化失败率较经典弗洛依德算法低,算法表现较好,在不同网络结构下性能表现较稳定,寻优能力更强。综合所有仿真实验可以得出,改进的弗洛伊德算法在急救车救援调度中效率更高,出错率更低,能更好地对急救车辆进行调度。 图9 两种算法路由最短路径优化率的比较 本文针对应急救援过程中救护车辆智能调度这一难点问题,对相关算法进行比较验证。采取改进弗洛伊德算法对道路拥堵状况、医院救援物资情况、患者和医院的地理位置、车辆空闲状况等进行综合考虑,找到了最佳路径,为救护车辆的智能调度问题提供了一个切实可行的解决方案,有效提升了智能救助的信息化水平。3 弗洛伊德算法优化
3.1 权值优化
3.2 改进弗洛伊德算法步骤
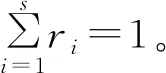
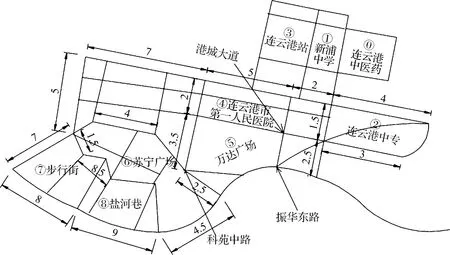
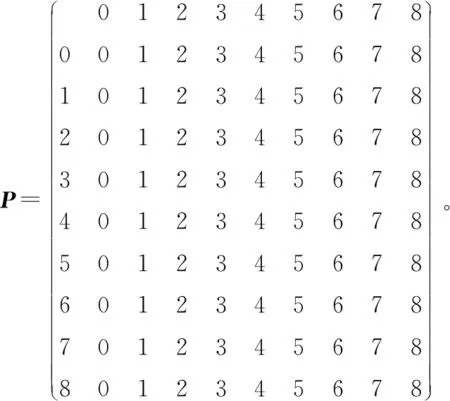
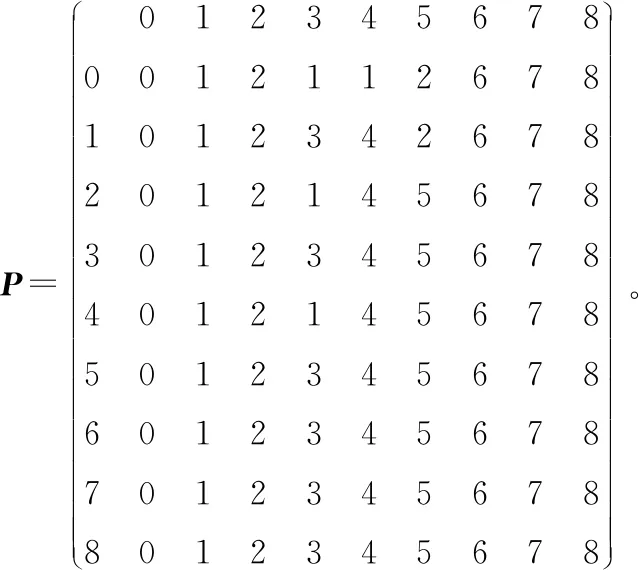
4 实例分析
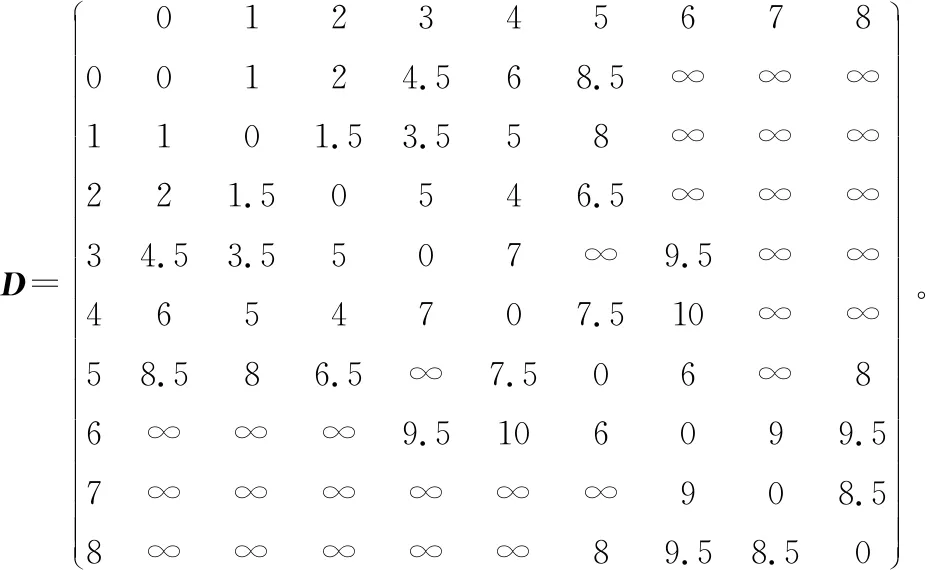
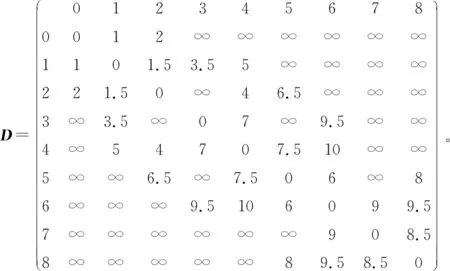
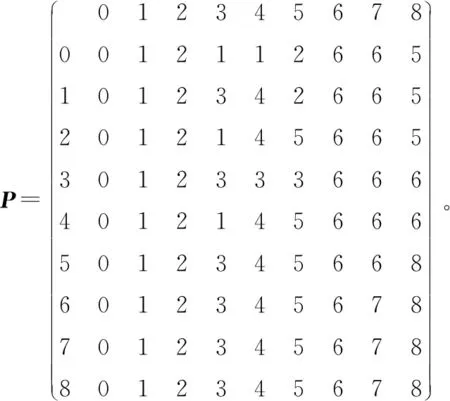
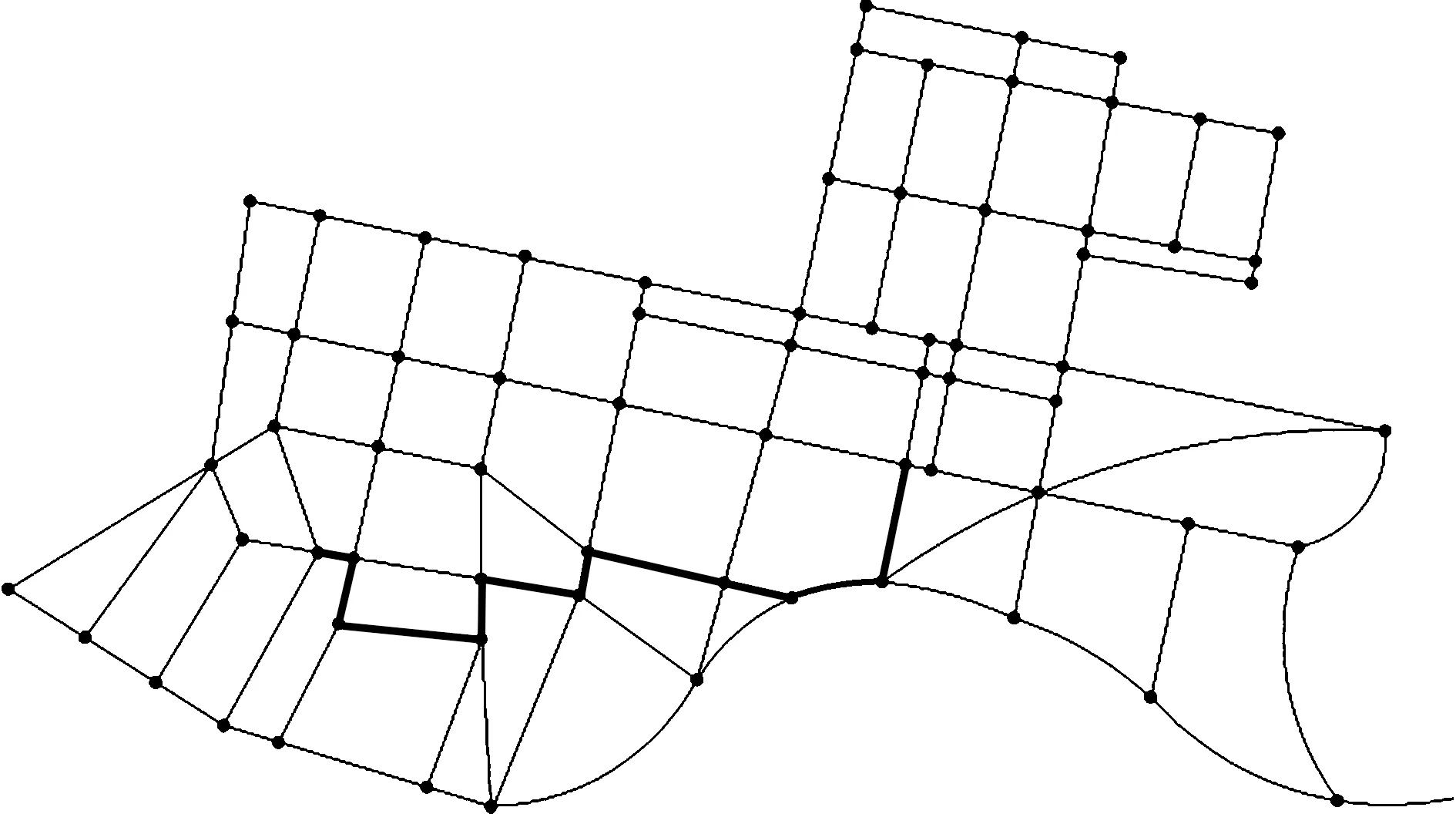
5 仿真实验结果与分析
5.1 网络结构的仿真实验
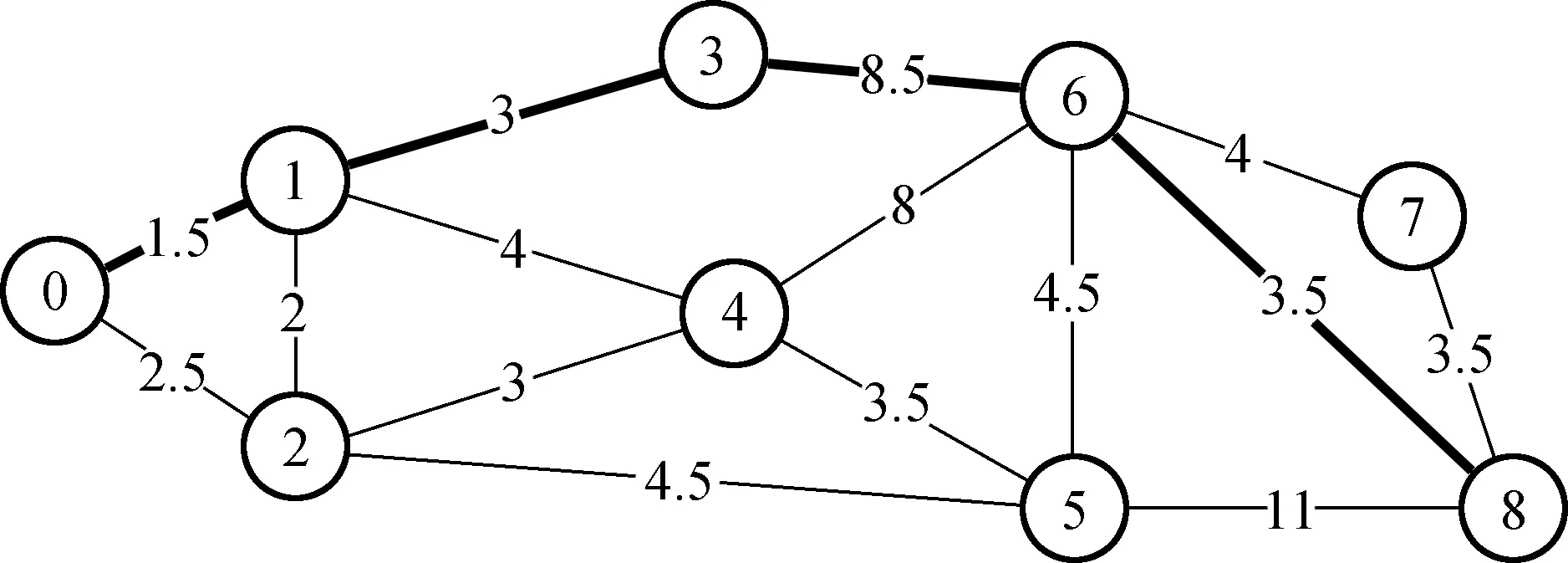
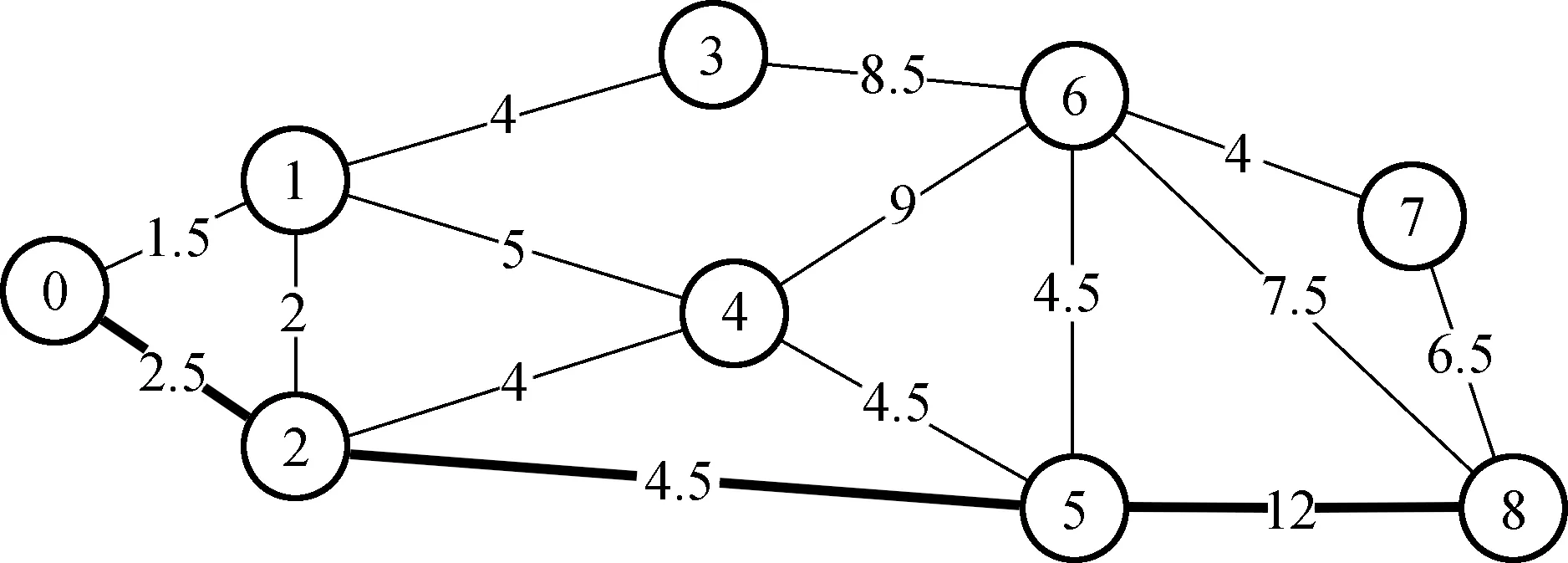

5.2 随机生成网络拓扑结构的仿真实验
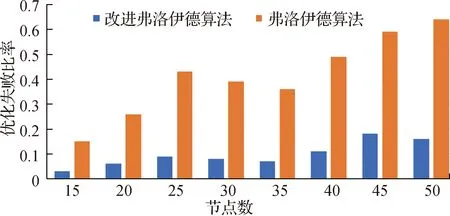
6 结语

