一类平面几何最值探秘

黄建栋 张淼

【摘要】 本文探究非局部平面中线长的最值.这类最值问题往往以求a+kb，或a+b+…（其中a，b，…是线段，k是系数）长的最值的形式出现.而a+b+…可视作a+kb当k=1时的推广.所以研究这类几何最值可以从研究不同的k值涉及何种最值入手.本文通过对k=0这种情况的深入研究，探得相应的解题策略.

【关键词】 几何;最值;求解;规律

平面几何最值，既有线长的最值.也有面积的最值.就最值所在平面来说，因整体与局部也会影响最值.本文仅涉及非局部平面中线长的最值.这类最值，本质上都是点与点间连线的最值，基本依据是两点之间线段最短;垂线段最短.但由于点有定点和动点之分，点的个数有不同，动点的轨迹有显或隐，有直线或圆，使之变化万千，造成解题困惑.为此，找出这类最值问题解题的一般规律，就显得十分必要.

通过对这类平面几何最值问题的综合思考.作者认为所有这类平面几何最值问题，皆是求a+kb或a+b+…（其中a，b，…是线段，k是系数）长的最值，而a+b+…可视作a+kb，当k=1时的推广.因此，只要就a+kb中不同的k，研究不同解题方法即可.本文仅就k=0作探究.

当k=0时，即求一条线段的最值.这类问题，解题的关键是先求得动点运动的轨迹，或借助旋转变换、位似变换，转换点的位置求解;当动点轨迹已知时，往往要把几何最值结合代数方法或转化为代数最值求解.

例1 如图1，AB为⊙O的直径，C，D为半圆上的动点，且∠COD=90°.连接AC，BD交于点E，F为OB的中点.若AB=4，求EF的最小值.

分析 本題F为定点，E为动点，关键是寻找动点运动的轨迹.

由∠COD=90°，得∠CAB+∠DBA=45°，

所以∠AEB=135°.

点E在对AB张角为135°的一条圆弧上.设弧的圆心为P，则当P，F，E三点共线时，EF有最小值.（EF最小=22-5）

例2 如图2，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，点D是半径为4的⊙A上一点，连接BD，点M是BD的中点，求线段CM的最大值.

分析 点M随点D在⊙A上运动而运动.设AB的中点为O，连OM，

则OM=12AD=2，

所以随着点D在⊙A上运动，点M在半径为2的⊙O上运动，当C，O，M共线，且点M在CO的延长线上时，CM有最大值.（CM最大=7）

例3 （1）如图3，在Rt△ABC中，∠B=90°，AB=BC，且A，B在半径为3的⊙O上，当点A在⊙O上运动时，求OC的最小值.

（2）改（1）中的条件AB=AC为∠A=30°，如图4，其他不变，求OC的最小值.

分析 （1）本题中，C随A动而动，动点C的轨迹是什么？有一个公共顶点的一组相似三角形，当它的一组对应点在直线（或圆）上运动时，它的另一组对应点也必在直线（或圆）上运动，所以点C的运动轨迹也是圆.当AB是⊙O直径时，由于BC=AB，AB丄BC，所以只要作直径A′B，过B作BC′⊥A′B，且BC′=A′B.设BC′中点为P，则点C必在以BC′为直径的⊙P上运动，如图5，当点C在OP上时，OC有最小值.（OC最小=32-3）

（2）如图6，解法与（1）基本相同，所不同的是，因为∠A=30°，所以BC=3AB3，从而⊙P直径为23，OC的最小值为3.

值得指出的是，本题还有一种解法：鉴于OC在圆内，若能把它移到一点在圆上，另一点在圆外，也是一种方法.但这时就要用到旋转变换.对于（1）来说，连OB，把△OCB绕点B按顺时针旋转90°，即能达到目的，此时点C与点A重合.设O落在点O′的位置（图7），则当点A在OO′上时，O′A最小，即OC最小;但对（2）来说，如此旋转，点C不与点A重合，为此还要借助于位似变换（位似比3），使点C与点A重合（图8）.但用这种方法求解，增加了难度，也不容易理解.

例4 如图9，边长为3的等边三角形ABC的顶点A在x轴的正半轴上移动.∠AOD=30°，顶点B在射线OD上随之移动，求顶点C到原点O的最大距离.

分析 本题有两种解题方法.

方法1 正△ABC在运动过程中只改变位置关系，而不改变其数量关系.故其AB边上的中线（设为CM）长不变，而OC≤OM+MC.

当OC=OM+MC时有最大值.（此时OC过点M，又OC⊥AB，所以△OAB为等腰三角形，OM=3+332，MC=332，OC最大=33+3，图略）

0

方法2 为了解题方便，不妨动静互换，即△ABC不动，而∠AOB运动.这时，点O在对AB的张角为30°的圆弧上运动.设圆弧的圆心为P，连接CP并延长交圆弧于点O′，则O′C即为原点O到点C的最大距离.（如图10）

上述4例，动点的轨迹都是圆弧，但也有动点的轨迹是直线（射线、线段）的.

1

例5 如图11，在直角坐标系中，有等腰△ABC，∠CAB=120°，B（0，3），点C与原点O重合.当点C在x轴负半轴上运动时，点A随之运动，求OA的最小值.

分析 点C在x轴负半轴上运动，点A运动的轨迹必

为射线.

2

如图12，连接AA′，即有

△A′BA∽△C′OB（△C′CB），

所以∠BAA′=∠BOC′=90°，

从而知道点A运动的轨迹是过点A与AB垂直的射线AA′.所以又归结为点线最值问题，由此OA的最小值即是点O到射线AA′的垂线段的长OH.

（OH=32，即OA最小=32）

3

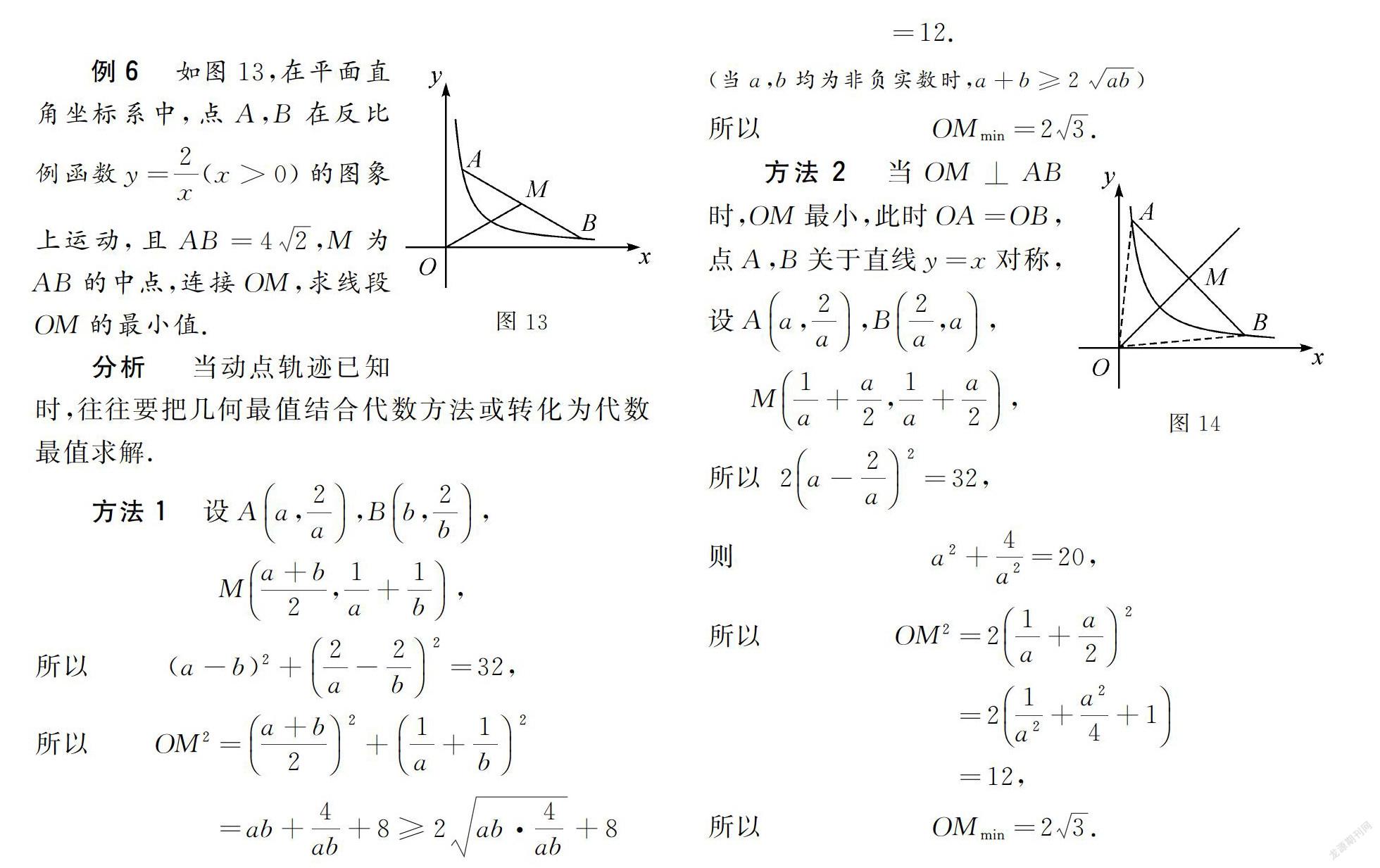
例6 如图13，在平面直角坐标系中，点A，B在反比例函数y=2x（x>0）的图象上运动，且AB=42，M为AB的中点，连接OM，求线段OM的最小值.

分析 当动点轨迹已知时，往往要把几何最值结合代数方法或转化为代数最值求解.

方法1 设Aa，2a，Bb，2b，

Ma+b2，1a+1b，

所以（a-b）2+2a-2b2=32，

所以OM2=a+b22+1a+1b2

=ab+4ab+8≥2ab·4ab+8

=12.

（当a，b均为非负实数时，a+b≥2ab）

所以OMmin=23.

4

方法2 当OM⊥AB时，OM最小，此时OA=OB，点A，B关于直线y=x对称，设Aa，2a，B2a，a，

M1a+a2，1a+a2，

所以2a-2a2=32，

则a2+4a2=20，

所以OM2=21a+a22

=21a2+a24+1

=12，

所以OMmin=23.