探究天津高考命题导向 提升数学抽象核心素养

■天津市第四中学 孟黎辉

近年来，天津高考命题保持着重基础、重素养，低起点、多层次、利区分的命题特色。从过去的题海战术，转向培育素养，成为高考命题的导向。下面，我们从数学抽象素养的提升来进一步探究。

抽象，是数学的基本特征，数学抽象是指通过对数量关系与空间形式的抽象，得到数学研究对象的素养，主要包括：从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系，从事物的具体背景中抽象出一般规律和结构，并用数学语言予以表征。

抽象起始于概念的获得，成熟于知识的理解，升华于知识的应用，抽象是知识迁移的必要条件。数学抽象是数学学科核心素养的重要组成部分，培养学生的抽象概括能力是数学学科的重要目标。在数学教学中，教师要抓好以下几点：

一、深刻理解概念，完善知识体系

对概念的深刻理解，是构建知识体系的重要一环，有的教师匆匆讲完基本概念、原理，学生还没有抽象出共性，没来得及内化为自己的知识体系，教师就开始讲例题，往往事倍功半，学生在做题中只知其然，不知其所以然，只能照着葫芦画瓢，机械模仿。因此，要深刻理解概念，必须要将概念中抽象的数学要素加以分析、提炼，只有这样，学生才具有进一步提升解决问题能力的保障。

二、设置情境模式，提升化归能力

数学抽象的最终目标是解决实际问题，让学生具备举一反三的能力，形成知识迁移。不能迁移的知识是不牢固的，只能在特定的情境下机械模仿，不是素质教育的目标。高考题一般以问题和情境为载体，数学情境的核心也是问题，因此，设计合理的问题情境，肩负育人和提高课堂效率两个重要任务。

教学应重视创设多样化的学习情境，让学生有机会唤起、验证知识，领会隐藏在知识背后的意义及思考这些信息是如何进行组织的。教师在教学中要精心设计好数学情境，由问题导入，强调在陌生情境中解决问题的能力培养，时刻关注学生的数学思想和方法的形成过程，杜绝无效的重复训练。

三、挖掘一题多解，提炼知识本质

数学抽象是数学的基本思想，是形成理性思维的重要基础，是数学的本质特征。一题多解，是数学学科提炼知识本质的重要途径。用不同的解题思路解决同一道题，看似消耗了时间和精力，实际上是将知识体系进一步整合。用这种方式抽象出来的数学知识，会更加接近知识的本源。在教学中，教师应该淡化程序化的解题模式，淡化解题技巧，强化通法通性，提升学生的应用能力。

四、善用习题变式，培养抽象素养

通过变式训练，让学生发现规律，抽象出同类习题的共性，在寻找共性的过程中，提炼出一般解题方法，并在此基础上，不断提高学生的实践能力，培养应用意识、创新意识。

我们对2018 年天津卷理科14 题进行研究，用4种方法求解，深入挖掘天津高考压轴小题的命题特点，指导复习备考。

例题：2018年（天津理）14题：

解法二（二次函数与一次函数模型）：函数y=x2+ 2ax+a与y=ax图像，若没有交点，则0 ＜a＜4；若有一个交点，则a= 4；若有两个交点，则a＞4或a＜0(舍)。

函数y=-x2+ 2ax- 2a与y=ax图像，若没有交点，则0 ＜a＜8；若有一个交点，则a= 8；若有两个交点，a＞8或a＜0(舍)。

综上可知，当4 ＜a＜8 时，函数y=f( )x与y=ax图像恰有两个交点，即f( )x=ax恰有2 个互异的实数解。

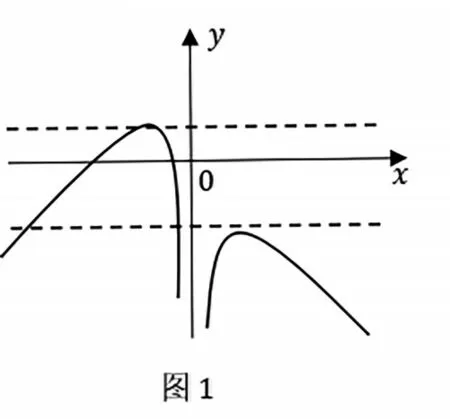
图1

解法四（其他型函数）：当x≤0 时，方程f(x)=ax，即x2+ 2ax+a=ax. 整理可得：x2=-a(x+ 1)，∵x=-1 不是方程的实数解，∴a=

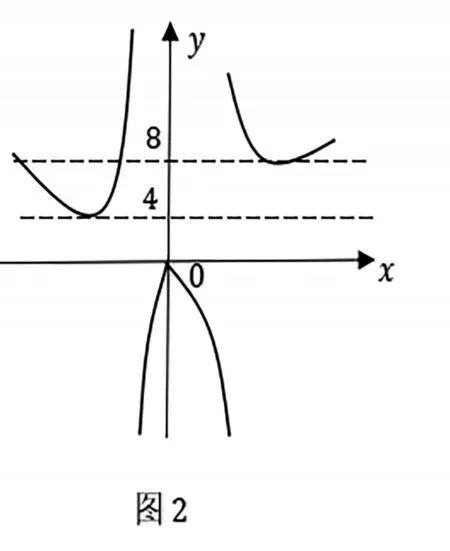
图2

从本题目解法中，我们看到，无论哪一种解法，都需要将函数、方程、不等式之间的关系进行抽象整合，再运用到函数图像情境中去，历经用数学语言表述、将已知条件等价转化、应用数学方法求解等环节，整个过程呈现出对数学抽象、逻辑推理等方面能力较高的要求。

从上面天津高考题中可以看出，命题者淡化解题技巧，力求考查学生对数学本质的抽象、逻辑推理等方面能力，从而甄别出考生对知识理解的深度以及不同的能力水平，将数学教学导向发展学生素养的学科价值和育人价值上。

在教学中，教师要深知数学素养是数学抽象、逻辑推理、数学运算、数学建模、直观想象、数据分析等方面的有机结合，它们相辅相成，每一方面的发展都离不开其他方面。拿数学运算来说，运算的基础是数学概念、定理和公式，离不开抽象思维和逻辑推理，在教学实践中如果为了“算”而“算”，就会掉入“重训练、轻思考；重结果、轻过程”的模式，运算能力反而不容易提高。其实，学生在学习数学中屡屡受挫，很多时候是因为对概念、定理、公式、方法的本质内容提炼不够，导致无法形成有效迁移。此外，有些教师在训练过程中过多强调“模型”和“技巧”的运用，忽视了学生自身抽象、提炼的过程，使学习只停留在模仿的层面上，一旦题目发生变化，就会束手无策。

高考分数不是评价学生学习效果的唯一指标，数学教学应立足于核心素养的培养，让学生勇于探究、敢于质疑、善于反思。教师在教学过程中，积极鼓励学生进行抽象提炼、大胆创新、积极应用，并给予及时的、肯定的、过程性评价，把数学核心素养落实到数学教育的各个环节。